4.1 : Tarifs connexes

Last updated
Save as PDF

Page ID: 197646

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Exprimez les quantités changeantes en termes de dérivés.
Trouvez les relations entre les dérivés d'un problème donné.
Utilisez la règle de chaîne pour déterminer le taux de variation d'une quantité qui dépend du taux de variation des autres quantités.

Nous avons vu que pour les quantités qui évoluent dans le temps, les taux auxquels ces quantités évoluent sont donnés par des dérivés. Si deux quantités connexes changent au fil du temps, les taux auxquels les quantités changent sont liés. Par exemple, si un ballon est rempli d'air, le rayon du ballon et le volume du ballon augmentent. Dans cette section, nous examinons plusieurs problèmes dans lesquels deux ou plusieurs quantités apparentées changent et nous étudions comment déterminer la relation entre les taux de variation de ces quantités.

Configuration des problèmes liés aux taux

Dans de nombreuses applications du monde réel, les quantités associées changent en fonction du temps. Par exemple, si nous reprenons l'exemple du ballon, nous pouvons dire que le taux de variation du volume$V$,, est lié au taux de variation du rayon,$r$. Dans ce cas, nous disons cela$\frac{dV}{dt}$ et$\frac{dr}{dt}$ sommes des taux connexes parce que$V$ c'est lié à$r$. Nous étudions ici plusieurs exemples de quantités connexes qui évoluent dans le temps et nous examinons comment calculer un taux de variation en fonction d'un autre taux de variation.

Exemple$\PageIndex{1}$: Inflating a Balloon

Un ballon sphérique est rempli d'air à la vitesse constante de$2\,\text{cm}^3\text{/sec}$ (Figure$\PageIndex{1}$). À quelle vitesse le rayon augmente-t-il lorsque le rayon est de$3$ cm ?

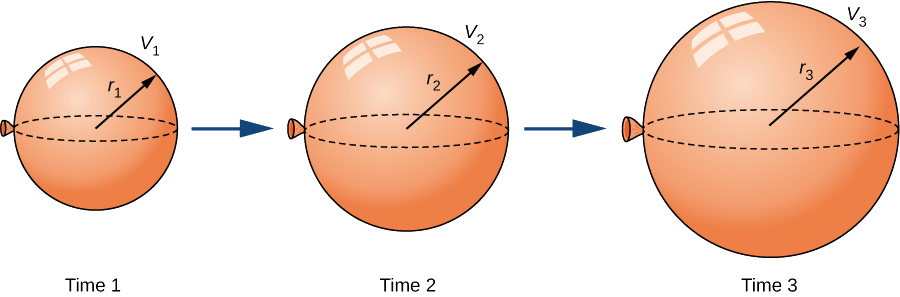
Trois ballons sont présentés aux heures 1, 2 et 3. Ces bulles augmentent en volume et en rayon à mesure que le temps passe. — Figure$\PageIndex{1}$ : Au fur et à mesure que le ballon se remplit d'air, son rayon et son volume augmentent avec le temps.

Solution

Le volume d'une sphère de rayon ($r$centimètres) est

$V=\frac{4}{3}πr^3\,\text{cm}^3.$

Comme le ballon est rempli d'air, le volume et le rayon sont fonction du temps. Par conséquent,$t$ quelques secondes après avoir commencé à remplir le ballon d'air, le volume d'air dans le ballon est

$V(t)=\frac{4}{3}π\big[r(t)\big]^3\text{cm}^3.$

En différenciant les deux côtés de cette équation par rapport au temps et en appliquant la règle de la chaîne, nous voyons que le taux de variation du volume est lié au taux de variation du rayon par l'équation

$V'(t)=4π\big[r(t)\big]^2r′(t).$

Le ballon est rempli d'air à un taux constant de$2 \,\text{cm}^3\text{/sec}$, donc$V'(t)=2\,\text{cm}^3\text{/sec}$. Par conséquent,

$2\,\text{cm}^3\text{/sec}=\Big(4π\big[r(t)\big]^2\;\text{cm}^2\Big)⋅\Big(r'(t)\;\text{cm/s}\Big),$

ce qui implique

$r'(t)=\dfrac{1}{2π\big[r(t)\big]^2}\;\text{cm/sec}$.

Lorsque le rayon$r=3$ cm,

$r'(t)=\dfrac{1}{18π}\;\text{cm/sec}.$

Exercice$\PageIndex{1}$

Quel est le taux de variation instantané du rayon en$r=6$ cm ?

Allusion: $\dfrac{dr}{dt}=\dfrac{1}{2πr^2}$

Réponse: $\frac{1}{72π}$cm/sec, soit environ 0,0044 cm/sec

Avant d'examiner d'autres exemples, décrivons la stratégie de résolution de problèmes que nous utiliserons pour résoudre les problèmes liés aux taux.

Stratégie de résolution de problèmes : résoudre un problème de taux connexes

Attribuez des symboles à toutes les variables impliquées dans le problème. Dessinez une figure, le cas échéant.
Indiquez, en termes de variables, les informations fournies et le taux à déterminer.
Trouvez une équation reliant les variables introduites à l'étape 1.
À l'aide de la règle de chaîne, différenciez les deux côtés de l'équation trouvée à l'étape 3 par rapport à la variable indépendante. Cette nouvelle équation mettra en relation les dérivées.
Remplacez toutes les valeurs connues dans l'équation de l'étape 4, puis résolvez pour obtenir le taux de variation inconnu

Notez que lorsque vous résolvez un problème de taux connexes, il est essentiel de ne pas substituer des valeurs connues trop tôt. Par exemple, si la valeur d'une quantité variable est substituée dans une équation avant que les deux côtés de l'équation ne soient différenciés, cette quantité se comportera comme une constante et sa dérivée n'apparaîtra pas dans la nouvelle équation trouvée à l'étape 4. Nous examinons cette erreur potentielle dans l'exemple suivant.

Exemples du processus

Mettons maintenant en œuvre la stratégie qui vient d'être décrite pour résoudre plusieurs problèmes liés aux taux. Le premier exemple concerne un avion survolant. La relation que nous étudions se situe entre la vitesse de l'avion et la vitesse à laquelle la distance entre l'avion et une personne au sol change.

Exemple$\PageIndex{2}$: An Airplane Flying at a Constant Elevation

Un avion survole à une altitude constante de$4000$ pieds. Un homme regarde l'avion depuis une position à quelques$3000$ mètres de la base d'une tour radio. L'avion vole horizontalement loin de l'homme. Si l'avion vole à une vitesse de pieds par$600$ seconde, à quelle vitesse la distance entre l'homme et l'avion augmente-t-elle lorsque l'avion passe au-dessus de la tour radio ?

Solution

Étape 1 Dessinez une image en introduisant des variables pour représenter les différentes quantités impliquées.

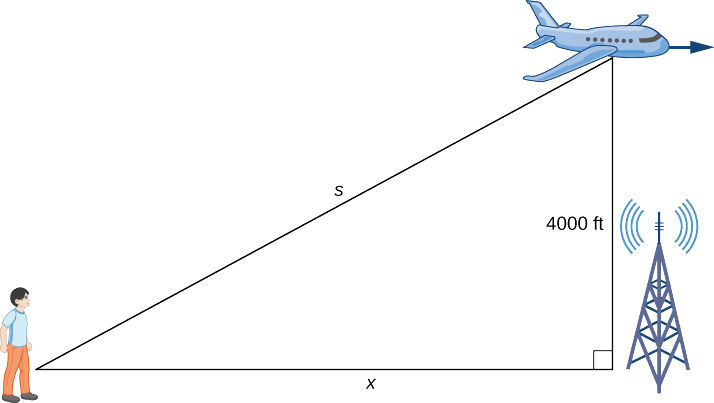
Un triangle droit est formé avec une personne au sol, un avion dans les airs et une tour radio à angle droit au sol. L'hypoténuse est s, la distance au sol entre la personne et la tour radio est x, et le côté opposé à la personne (c'est-à-dire la hauteur entre le sol et l'avion) est de 4 000 pieds. — Figure$\PageIndex{2}$ : Un avion vole à une hauteur constante de$4000$ pieds. La distance entre la personne et l'avion et la personne et l'endroit au sol directement sous l'avion changent. Nous désignons ces quantités avec les variables$s$ et$x$, respectivement.

Comme indiqué,$x$ indique la distance entre l'homme et sa position au sol directement sous l'avion. La variable$s$ indique la distance entre l'homme et l'avion. Notez que les deux$x$ et$s$ sont des fonctions du temps. Nous n'introduisons pas de variable pour la hauteur de l'avion car celui-ci reste à une altitude constante de$4000$ pieds. Comme la hauteur d'un objet au-dessus du sol est mesurée comme la distance la plus courte entre l'objet et le sol, le segment de ligne d'une longueur de 4 000 pieds est perpendiculaire au segment de ligne d'une longueur de$x$ pieds, créant ainsi un triangle droit.

Étape 2 Puisque$x$ indique la distance horizontale entre l'homme et le point au sol sous l'avion,$dx/dt$ représente la vitesse de l'avion. On nous dit que la vitesse de l'avion est de$600$ pieds par seconde. Par conséquent,$\frac{dx}{dt}=600$ pieds par seconde. Comme on nous demande de déterminer le taux de variation de la distance entre l'homme et l'avion lorsque l'avion se trouve directement au-dessus de la tour radio, nous devons déterminer$ds/dt$ quand$x=3000$ ft.

Étape 3 À partir de la figure, nous pouvons utiliser le théorème de Pythagore pour écrire une équation reliant$x$ et$s$ :

$[x(t)]^2+4000^2=[s(t)]^2.$

Étape 4. En différenciant cette équation par rapport au temps et en utilisant le fait que la dérivée d'une constante est nulle, nous arrivons à l'équation

\[x\frac{dx}{dt}=s\frac{ds}{dt}.\nonumber \]

Étape 5. Déterminez la vitesse à laquelle la distance entre l'homme et l'avion augmente lorsque l'avion passe directement au-dessus de la tour radio. Autrement dit, trouvez$\frac{ds}{dt}$ quand$x=3000$ ft. Puisque la vitesse de l'avion est de pieds par$600$ seconde, nous savons qu'elle est en$\frac{dx}{dt}=600$ pieds par seconde. On ne nous donne pas de valeur explicite pour$s$ ; cependant, puisque nous essayons de déterminer$\frac{ds}{dt}$ quand$x=3000$ ft, nous pouvons utiliser le théorème de Pythagore pour déterminer la distance$s$ lorsque$x=3000$ ft et la hauteur est$4000$ ft. Résoudre l'équation

$3000^2+4000^2=s^2$

car$s$, nous avons des$s=5000$ pieds au moment de l'intérêt. À l'aide de ces valeurs, nous concluons que$ds/dt$

est une solution de l'équation

$(3000)(600)=(5000)⋅\dfrac{ds}{dt}$.

Par conséquent,

$\dfrac{ds}{dt}=\dfrac{3000⋅600}{5000}=360\,\text{ft/sec}.$

Remarque : Lorsque vous résolvez des problèmes de taux connexes, il est important de ne pas substituer trop rapidement des valeurs aux variables. Par exemple, à l'étape 3, nous avons lié les quantités variables$x(t)$ et$s(t)$ par l'équation

$[x(t)]^2+4000^2=[s(t)]^2.$

Comme le plan reste à une hauteur constante, il n'est pas nécessaire d'introduire une variable pour la hauteur, et nous sommes autorisés à utiliser la constante 4000 pour indiquer cette quantité. Cependant, les deux autres quantités sont en train de changer. Si nous l'avions remplacée$x(t)=3000$ par erreur avant de différencier, notre équation aurait été

$3000^2+4000^2=[s(t)]^2.$

Après avoir différencié, notre équation deviendrait

$0=s(t)\dfrac{ds}{dt}.$

Par conséquent, nous concluons à tort que$\frac{ds}{dt}=0.$

Exercice$\PageIndex{2}$

Quelle est la vitesse de l'avion si la distance entre la personne et l'avion augmente à un rythme de$300$ pieds par seconde ?

Allusion: $\dfrac{ds}{dt}=300$pieds/seconde

Réponse: $500$pieds/seconde

Nous revenons maintenant au problème du lancement de fusées depuis le début du chapitre.

Exemple$\PageIndex{3}$: Chapter Opener - A Rocket Launch

Une fusée est lancée de telle sorte qu'elle s'élève verticalement. Une caméra est positionnée à$5000$ quelques pas de la rampe de lancement. Lorsque la fusée se trouve à$1000$ pieds au-dessus de la rampe de lancement, sa vitesse est de$600$ pieds par seconde.

Une photo d'une fusée qui décolle. — Figure$\PageIndex{3}$ : (source : modification de l'œuvre de Steve Jurvetson, Wikimedia Commons)

Trouvez le taux de variation nécessaire de l'angle de la caméra en fonction du temps pour qu'elle reste focalisée sur la fusée.

Solution

Étape 1 Dessinez une image en introduisant les variables.

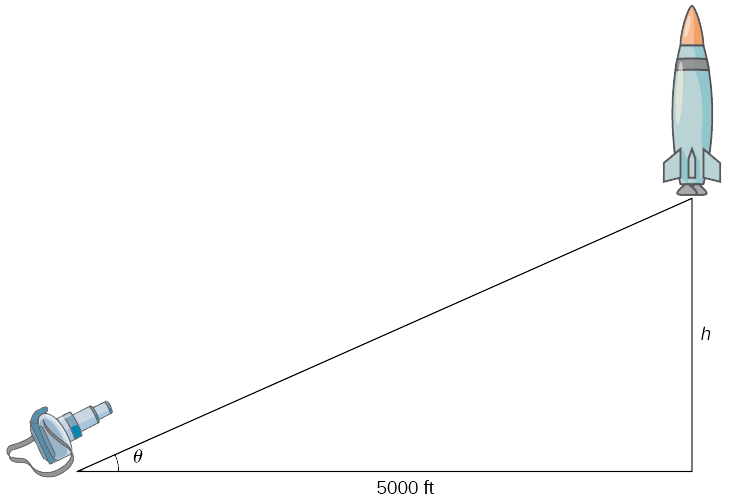
Un triangle droit est formé avec une caméra à l'un des angles non droits et une fusée à l'autre angle non droit. L'angle avec la caméra a la mesure θ. La distance entre la fusée et le sol est h ; notez qu'il s'agit du côté opposé à l'angle de mesure θ. Le côté adjacent à l'angle avec la mesure θ est de 5 000 pieds. — Figure$\PageIndex{4}$ : Une caméra est positionnée à$5000$ quelques mètres de la rampe de lancement de la fusée. La hauteur de la fusée et l'angle de la caméra changent en fonction du temps. Nous désignons ces quantités avec les variables$h$ et$θ$, respectivement.

$h$Soit la hauteur de la fusée au-dessus de la rampe de lancement et$θ$ l'angle entre l'objectif de la caméra et le sol.

Étape 2 Nous essayons de déterminer le taux de variation de l'angle de la caméra par rapport au temps pendant lequel la fusée se trouve à 1 000 pieds du sol. Autrement dit, nous devons trouver$\frac{dθ}{dt}$ quand$h=1000$ ft. À ce moment-là, nous savons que la vitesse de la fusée est de$\frac{dh}{dt}=600$ pieds par seconde.

Étape 3 Nous devons maintenant trouver une équation reliant les deux quantités qui changent par rapport au temps :$h$ et$θ$. Comment créer une telle équation ? En utilisant le fait que nous avons dessiné un triangle droit, il est naturel de penser aux fonctions trigonométriques. Rappelez-vous qu'$\tan θ$il s'agit du rapport entre la longueur du côté opposé du triangle et la longueur du côté adjacent. Ainsi, nous avons

$\tan θ=\dfrac{h}{5000}$.

Cela nous donne l'équation

$h=5000\tan θ.$

Étape 4. En différenciant cette équation par rapport au temps$t$, nous obtenons

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}$.

Étape 5. Nous voulons savoir$\frac{dθ}{dt}$ quand$h=1000$ ft. À l'heure actuelle, nous savons que$\frac{dh}{dt}=600$ ft/sec. Nous devons déterminer$\sec^2θ$. Rappelons que$\sec θ$ c'est le rapport entre la longueur de l'hypoténuse et la longueur du côté adjacent. Nous savons que la longueur du côté adjacent est de$5000$ pieds. Pour déterminer la longueur de l'hypoténuse, nous utilisons le théorème de Pythagore, où la longueur d'une jambe est de$5000$ pieds, la longueur de l'autre jambe est de$h=1000$ pieds et la longueur de l'hypoténuse est de$c$ pieds, comme le montre la figure suivante.

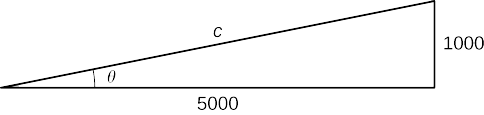
$Un triangle droit possède un angle avec la mesure θ. L'hypoténuse est c, la longueur du côté opposé à l'angle avec la mesure θ est de 1000 et le côté adjacent à l'angle avec la mesure θ est de 5000.$

Nous voyons que

$1000^2+5000^2=c^2$

et nous concluons que l'hypoténuse est

$c=1000\sqrt{26}\,\text{ft}.$

Par conséquent, lorsque$h=1000,$ nous avons

$\sec^2θ=\left(\dfrac{1000\sqrt{26}}{5000}\right)^2=\dfrac{26}{25}.$

Rappelons dès l'étape 4 que l'équation relative$\frac{dθ}{dt}$ à nos valeurs connues est

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}.$

Quand$h=1000$ ft, nous savons que$\frac{dh}{dt}=600$ ft/sec et$\sec^2θ=\frac{26}{25}$. En substituant ces valeurs à l'équation précédente, nous arrivons à l'équation

$600=5000\left(\frac{26}{25}\right)\dfrac{dθ}{dt}$.

Par conséquent,$\dfrac{dθ}{dt}=\dfrac{3}{26}$ rad/sec.

Exercice$\PageIndex{3}$

Quel est le taux de variation nécessaire pour l'angle d'élévation de la caméra si la caméra est placée au sol à une distance de$4000$ pieds de la rampe de lancement et que la vitesse de la fusée est de pieds par$500$ seconde lorsque la fusée se trouve à$2000$ pieds du sol ?

Allusion: Trouvez$\frac{dθ}{dt}$ quand$h=2000$ ft. À cette époque,$\frac{dh}{dt}=500$ pieds par seconde.

Réponse: $\frac{1}{10}$rad/sec

Dans l'exemple suivant, nous considérons l'eau s'écoulant d'un entonnoir en forme de cône. Nous comparons la vitesse à laquelle le niveau d'eau dans le cône diminue avec la vitesse à laquelle le volume d'eau diminue.

Exemple$\PageIndex{4}$: Water Draining from a Funnel

L'eau s'écoule du fond d'un entonnoir en forme de cône à raison de$0.03\,\text{ft}^3\text{/sec}$. La hauteur de l'entonnoir est de$2$ pieds et le rayon au sommet de l'entonnoir est de$1$ pieds. À quelle vitesse la hauteur de l'eau dans l'entonnoir change-t-elle lorsque la hauteur de l'eau est de$\frac{1}{2}$ pieds ?

Solution

Étape 1 : Dessinez une image en introduisant les variables.

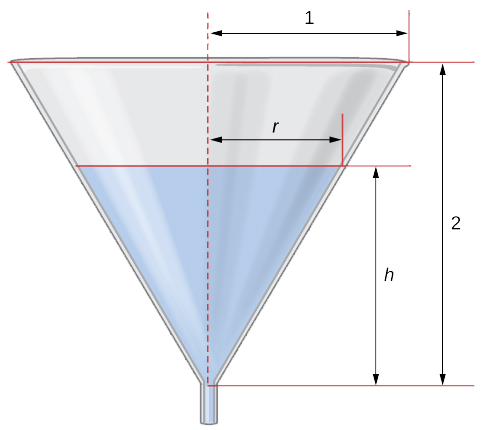
Un entonnoir est représenté avec une hauteur de 2 et un rayon de 1 en haut. L'entonnoir contient de l'eau à la hauteur h, point auquel le rayon est r. — Figure$\PageIndex{5}$ : L'eau s'écoule d'un entonnoir d'une hauteur de$2$ pieds et d'un rayon de$1$ pieds. La hauteur et le rayon de l'eau évoluent au fil du temps. Nous désignons ces quantités avec les variables$h$ et$r$, respectivement.

$h$Soit la hauteur de l'eau dans l'entonnoir, r le rayon de l'eau à sa surface$V$ et le volume de l'eau.

Étape 2 : Nous devons déterminer$\frac{dh}{dt}$ quand$h=\frac{1}{2}$ ft. Nous savons que$\frac{dV}{dt}=−0.03$ ft/sec.

Étape 3 : Le volume d'eau dans le cône est

$V=\frac{1}{3}πr^2h.$

Sur la figure, nous voyons que nous avons des triangles similaires. Par conséquent, le rapport des côtés des deux triangles est le même. Par conséquent,$\frac{r}{h}=\frac{1}{2}$ ou$r=\frac{h}{2}.$ en utilisant ce fait, l'équation du volume peut être simplifiée pour

$V=\frac{1}{3}π\left(\frac{h}{2}\right)^2h=\frac{π}{12}h^3$.

Étape 4 : En appliquant la règle de la chaîne tout en différenciant les deux côtés de cette équation par rapport au temps$t$, nous obtenons

\[\frac{dV}{dt}=\frac{π}{4}h^2\frac{dh}{dt}.\nonumber \]

Étape 5 : Nous voulons savoir$\frac{dh}{dt}$ quand$h=\frac{1}{2}$ ft. Puisque l'eau part au rythme de$0.03\,\text{ft}^3\text{/sec}$, nous le savons$\frac{dV}{dt}=−0.03\,\text{ft}^3\text{/sec}$. Par conséquent,

\[−0.03=\frac{π}{4}\left(\frac{1}{2}\right)^2\dfrac{dh}{dt},\nonumber \]

ce qui implique

\[−0.03=\frac{π}{16}\dfrac{dh}{dt}.\nonumber \]

Il s'ensuit que

\[\dfrac{dh}{dt}=−\frac{0.48}{π}=−0.153\,\text{ft/sec}.\nonumber \]

Exercice$\PageIndex{4}$

À quelle vitesse la hauteur de l'eau change-t-elle lorsque la hauteur de l'eau est de$\frac{1}{4}$ pieds ?

Allusion: Nous devons trouver$\frac{dh}{dt}$ quand$h=\frac{1}{4}.$

Réponse: $−0.61$pieds/seconde

Concepts clés

Pour résoudre un problème de taux connexe, commencez par dessiner une image illustrant la relation entre les deux ou plusieurs quantités connexes qui changent dans le temps.
En termes de quantités, indiquer les informations fournies et le taux à trouver.
Trouvez une équation reliant les quantités.
Utilisez la différenciation, en appliquant la règle de la chaîne si nécessaire, pour trouver une équation qui relie les taux.
Veillez à ne pas substituer une quantité variable à l'une des variables avant d'avoir trouvé une équation reliant les taux.

Lexique

taux connexes: sont des taux de variation associés à au moins deux quantités connexes qui évoluent au fil du temps

Exemple\(\PageIndex{1}\): Inflating a Balloon

Exercice\(\PageIndex{1}\)

Stratégie de résolution de problèmes : résoudre un problème de taux connexes

Exemple\(\PageIndex{2}\): An Airplane Flying at a Constant Elevation

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Chapter Opener - A Rocket Launch

Exercice\(\PageIndex{3}\)

Exemple\(\PageIndex{4}\): Water Draining from a Funnel

Exercice\(\PageIndex{4}\)