3.8 : Différenciation implicite
- Page ID
- 197807
- Trouvez la dérivée d'une fonction complexe en utilisant la différenciation implicite.
- Utilisez la différenciation implicite pour déterminer l'équation d'une tangente.
Nous avons déjà étudié comment trouver des équations de lignes tangentes à des fonctions et le taux de variation d'une fonction à un point spécifique. Dans tous ces cas, nous avions l'équation explicite de la fonction et nous avons différencié ces fonctions de manière explicite. Supposons plutôt que nous souhaitions déterminer l'équation d'une tangente à une courbe arbitraire ou le taux de variation d'une courbe arbitraire en un point. Dans cette section, nous résolvons ces problèmes en trouvant les dérivées de fonctions qui définissent\(y\) implicitement en termes de\(x\).
Différenciation implicite
Dans la plupart des discussions sur les mathématiques, si la variable dépendante\(y\) est fonction de la variable indépendante\(x\), nous exprimons y en termes de\(x\). Si tel est le cas, nous disons que\(y\) c'est une fonction explicite de\(x\). Par exemple, lorsque nous écrivons l'équation\(y=x^2+1\), nous définissons y explicitement en termes de\(x\). D'autre part, si la relation entre la fonction\(y\) et la variable\(x\) est exprimée par une équation où elle n'\(y\)est pas entièrement exprimée en termes de\(x\), nous disons que l'équation définit\(y\) implicitement en termes de\(x\). Par exemple, l'équation\(y−x^2=1\) définit\(y=x^2+1\) implicitement la fonction.
La différenciation implicite nous permet de déterminer les pentes des tangentes à des courbes qui ne sont clairement pas des fonctions (elles échouent au test de la ligne verticale). Nous utilisons l'idée que des parties de\(y\) sont des fonctions qui répondent à l'équation donnée, mais que y n'est pas réellement une fonction de\(x\).
En général, une équation définit implicitement une fonction si la fonction satisfait à cette équation. Une équation peut définir implicitement de nombreuses fonctions différentes. Par exemple, les fonctions
\[y=\sqrt{25−x^2}\nonumber \]
et
\[y=\begin{cases}\sqrt{25−x^2}, & \text{if }−5≤x<0\\ −\sqrt{25−x^2}, & \text{if }0≤x≤5\end{cases}\nonumber \]
qui sont illustrées dans la figure\(\PageIndex{1}\), ne sont que deux des nombreuses fonctions définies implicitement par l'équation\(x^2+y^2=25\).
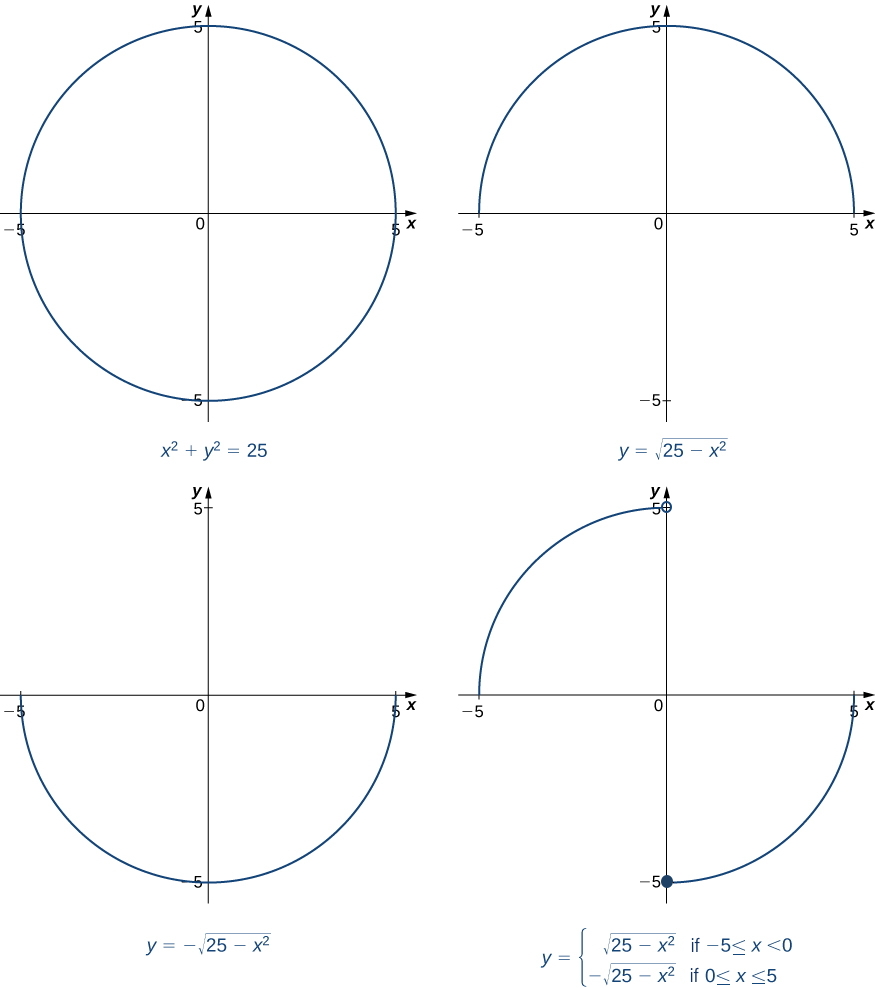
Si nous voulons trouver la pente de la droite tangente au graphe d'\(x^2+y^2=25\)au point\((3,4)\), nous pouvons évaluer la dérivée de la fonction\(y=\sqrt{25−x^2}\) at\(x=3\). D'un autre côté, si nous voulons connaître la pente de la tangente au point\((3,−4)\), nous pouvons utiliser la dérivée de\(y=−\sqrt{25−x^2}\). Cependant, il n'est pas toujours facile de le résoudre pour une fonction définie implicitement par une équation. Heureusement, la technique de différenciation implicite nous permet de trouver la dérivée d'une fonction implicitement définie sans jamais résoudre la fonction de manière explicite. Le processus de recherche\(\dfrac{dy}{dx}\) à l'aide de la différenciation implicite est décrit dans la stratégie de résolution de problèmes suivante.
Pour effectuer une différenciation implicite sur une équation qui définit\(y\) implicitement une fonction en termes de variable\(x\), procédez comme suit :
- Prenez la dérivée des deux côtés de l'équation. Gardez à l'esprit que\(y\) c'est une fonction de\(x\). Par conséquent, alors que\[\dfrac{d}{dx}(\sin x)=\cos x\nonumber \] et\[\dfrac{d}{dx}(\sin y)=\cos y\cdot\dfrac{dy}{dx}\nonumber \] parce que nous devons utiliser la règle de la chaîne pour différencier\(\sin y\) par rapport à\(x\).
- Réécrivez l'équation de manière à ce que tous les termes contenant\(dy/dx\) se trouvent à gauche et que tous les termes qui n'en contiennent pas\(dy/dx\) soient à droite.
- Facteur\(dy/dx\) sur la gauche.
- Résolvez\(dy/dx\) en divisant les deux côtés de l'équation par une expression algébrique appropriée.
En supposant que cela\(y\) soit défini implicitement par l'équation\(x^2+y^2=25\), trouvez\(\dfrac{dy}{dx}\).
Solution
Suivez les étapes de la stratégie de résolution des problèmes.
| \(\dfrac{d}{dx}(x^2+y^2)=\dfrac{d}{dx}(25)\) | Étape 1 Différenciez les deux côtés de l'équation. |
| \(\dfrac{d}{dx}(x^2)+\dfrac{d}{dx}(y^2)=0\) | Étape 1.1. Utilisez la règle de somme sur la gauche. Sur la droite\(\dfrac{d}{dx}(25)=0\). |
| \(2x+2y\dfrac{dy}{dx}=0\) | Étape 1.2. Prenez les dérivés, ainsi\(\dfrac{d}{dx}(x^2)=2x\) et\(\dfrac{d}{dx}(y^2)=2y\dfrac{dy}{dx}\). |
| \(2y\dfrac{dy}{dx}=−2x\) | Étape 2 Conservez les termes\(\dfrac{dy}{dx}\) sur la gauche. Déplacez les termes restants vers la droite. |
| \(\dfrac{dy}{dx}=−\dfrac{x}{y}\) | Étape 4. Divisez les deux côtés de l'équation par\(2y\). (L'étape 3 ne s'applique pas dans ce cas.) |
Analyse
Notez que l'expression résultante pour\(\dfrac{dy}{dx}\) est exprimée à la fois en termes de variable indépendante\(x\) et de variable dépendante\(y\). Bien que, dans certains cas, il soit possible de s'exprimer\(x\) uniquement\(\dfrac{dy}{dx}\) en termes, il n'est généralement pas possible de le faire.
En supposant que cela\(y\) soit défini implicitement par l'équation\(x^3\sin y+y=4x+3\), trouvez\(\dfrac{dy}{dx}\).
Solution
| \(\dfrac{d}{dx}(x^3\sin y+y)=\dfrac{d}{dx}(4x+3)\) | Étape 1 : Différenciez les deux côtés de l'équation. |
| \(\dfrac{d}{dx}(x^3\sin y)+\dfrac{d}{dx}(y)=4\) | Étape 1.1 : Appliquez la règle de somme sur la gauche. Sur la droite,\(\dfrac{d}{dx}(4x+3)=4\). |
| \(\left(\dfrac{d}{dx}(x^3)⋅\sin y+\dfrac{d}{dx}(\sin y)⋅x^3\right)+\dfrac{dy}{dx}=4\) | Étape 1.2 : Utilisez la règle du produit pour trouver\(\dfrac{d}{dx}(x^3\sin y)\). Observez cela\(\dfrac{d}{dx}(y)=\dfrac{dy}{dx}\). |
| \(3x^2\sin y+(\cos y\dfrac{dy}{dx})⋅x^3+\dfrac{dy}{dx}=4\) | Étape 1.3 : Nous le savons\(\dfrac{d}{dx}(x^3)=3x^2\). Utilisez la règle de chaîne pour obtenir\(\dfrac{d}{dx}(\sin y)=\cos y\dfrac{dy}{dx}\). |
| \(x^3\cos y\dfrac{dy}{dx}+\dfrac{dy}{dx}=4−3x^2\sin y\) | Étape 2 : Conservez tous les termes\(\dfrac{dy}{dx}\) contenus sur la gauche. Déplacez tous les autres termes vers la droite. |
| \(\dfrac{dy}{dx}(x^3\cos y+1)=4−3x^2\sin y\) | Étape 3 : Facteur\(\dfrac{dy}{dx}\) sur la gauche. |
| \(\dfrac{dy}{dx}=\dfrac{4−3x^2\sin y}{x^3\cos y+1}\) | Étape 4 : Résolvez\(\dfrac{dy}{dx}\) en divisant les deux côtés de l'équation par\(x^3\cos y+1\). |
\(\dfrac{d^2y}{dx^2}\)Trouve si\(x^2+y^2=25\).
Solution
Dans l'exemple\(\PageIndex{1}\), nous l'avons montré\(\dfrac{dy}{dx}=−\dfrac{x}{y}\). Nous pouvons prendre la dérivée des deux côtés de cette équation pour trouver\(\dfrac{d^2y}{dx^2}\).
\ (\ begin {align*} \ dfrac {d^2y} {dx^2} &= \ dfrac {d} {dy} \ left (− \ dfrac {x} {y} \ right) & \ text {Différenciez les deux côtés de} \ dfrac {dy} {dx} =− \ dfrac {x} {y}. \ \ [4pt]
&− \ dfrac {\ left (1⋅y−x \ dfrac {dy} {dx} \ right)} {y^2} & & \ text {Utilisez la règle du quotient pour trouver} \ dfrac {d} {dy} \ left (− \ dfrac {x} {y} \ right). \ \ [4 points]
&= \ dfrac {−y+x \ dfrac {dy} {dx}} {y^2} & & \ text {Simplifier.} \ \ [4 points]
&= \ dfrac {−y+x \ left (− \ dfrac {x} {y} \ right)} {y^2} & & & \ text {Substitut} \ dfrac {x} {y} \ right)} {y^2} & & & \ text {Substitut} \ dfrac {x} {y} \ right frac {dy} {dx} =− \ dfrac {x} {y}. \ \ [4pt]
&= \ dfrac {−y^2−x^2} {y^3} & & \ text {Simplifier.} \ end {align*} \)
À ce stade, nous avons trouvé une expression pour\(\dfrac{d^2y}{dx^2}\). Si nous le voulons, nous pouvons simplifier davantage l'expression en la rappelant\(x^2+y^2=25\) et en effectuant cette substitution dans le numérateur pour obtenir\(\dfrac{d^2y}{dx^2}=−\dfrac{25}{y^3}\).
Recherchez\(\dfrac{dy}{dx}\) pour\(y\) défini implicitement par l'équation\(4x^5+\tan y=y^2+5x\).
- Allusion
-
Suivez la stratégie de résolution des problèmes, en vous rappelant d'appliquer la règle de la chaîne pour différencier\(\tan y\) et\(y^2\).
- Réponse
-
\[\dfrac{dy}{dx}=\dfrac{5−20x^4}{\sec^2y−2y} \nonumber \]
Trouver implicitement des lignes tangentes
Maintenant que nous avons vu la technique de la différenciation implicite, nous pouvons l'appliquer au problème de la recherche d'équations de droites tangentes à des courbes décrites par des équations.
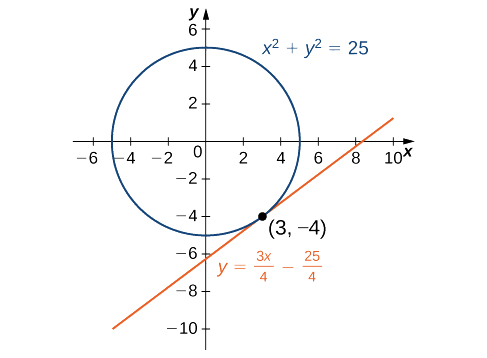
Détermine l'équation de la droite tangente à la courbe\(x^2+y^2=25\) au point\((3,−4)\).
Solution
Bien que nous ayons pu trouver cette équation sans utiliser de différenciation implicite, l'utilisation de cette méthode la rend beaucoup plus facile. Dans Exemple\(\PageIndex{1}\), nous avons trouvé\(\dfrac{dy}{dx}=−\dfrac{x}{y}\).
La pente de la tangente est déterminée en la substituant\((3,−4)\) dans cette expression. Par conséquent, la pente de la tangente est\(\dfrac{dy}{dx}\Big|_{(3,−4)}=−\dfrac{3}{−4}=\dfrac{3}{4}\).
En utilisant le point\((3,−4)\) et la pente\(\dfrac{3}{4}\) dans l'équation de pente ponctuelle de la droite, nous obtenons l'équation\(y=\dfrac{3}{4}x−\dfrac{25}{4}\) (Figure\(\PageIndex{2}\)).
Détermine l'équation de la droite tangente\(y^3+x^3−3xy=0\) au graphe du point\(\left(\frac{3}{2},\frac{3}{2}\right)\) (Figure\(\PageIndex{3}\)). Cette courbe est connue sous le nom de folium (ou feuille) de Descartes.
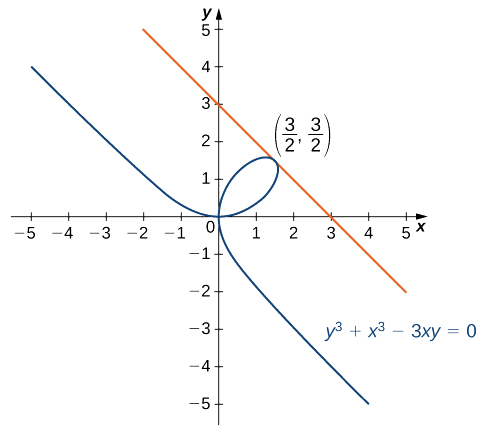
Solution
Commencez par trouver\(\dfrac{dy}{dx}\).
\(\dfrac{d}{dx}\big(y^3+x^3−3xy\big)=\dfrac{d}{dx}\big(0\big)\)
\(3y^2\dfrac{dy}{dx}+3x^2−\left(3y+3x\dfrac{dy}{dx}\right)=0\)
\(3y^2\dfrac{dy}{dx}+3x^2−3y-3x\dfrac{dy}{dx}=0\)
\(\left(3y^2-3x\right)\dfrac{dy}{dx}=3y-3x^2\)
\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\).
Ensuite, remplacez\(\left(\frac{3}{2},\frac{3}{2}\right)\) par\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\) pour trouver la pente de la tangente :
\(\dfrac{dy}{dx}\Bigg|_{\left(\frac{3}{2},\frac{3}{2}\right)}=−1\).
Enfin, remplacez-la par l'équation de pente ponctuelle de la droite pour obtenir
\(y=−x+3\).
Dans un jeu vidéo simple, une fusée se déplace sur une orbite elliptique dont la trajectoire est décrite par l'équation\(4x^2+25y^2=100\). La fusée peut tirer des missiles le long de lignes tangentes à sa trajectoire. Le but du jeu est de détruire un astéroïde entrant se déplaçant le long de l'\(x\)axe positif vers\((0,0)\). Si la roquette tire un missile alors qu'elle se trouve\(\left(3,\frac{8}{5}\right)\), où croisera-t-elle l'\(x\)axe Y ?
Solution
Pour résoudre ce problème, nous devons déterminer où la droite est tangente au graphe de
\(4x^2+25y^2=100\)à\(\left(3,\frac{8}{5}\right)\) l'intersection de l'\(x\)axe. Commencez par trouver\(\dfrac{dy}{dx}\) implicitement.
En nous différenciant, nous avons
\(8x+50y\dfrac{dy}{dx}=0.\)
Résoudre pour\(\dfrac{dy}{dx}\),
nous avons
\(\dfrac{dy}{dx}=−\dfrac{4x}{25y}\).
La pente de la tangente est\(\dfrac{dy}{dx}\Bigg|_{\left(3,\frac{8}{5}\right)}=−\dfrac{3}{10}\). L'équation de la tangente est\(y=−\dfrac{3}{10}x+\dfrac{5}{2}\). Pour déterminer l'intersection de la ligne avec l'\(x\)axe Y, résolvez\(0=−\dfrac{3}{10}x+\dfrac{5}{2}\). La solution est\(x=\dfrac{25}{3}\). Le missile croise l'\(x\)axe -au point\(\left(\frac{25}{3},0\right)\).
Détermine l'équation de la droite tangente à l'hyperbole\(x^2−y^2=16\) au point\((5,3)\).
- Allusion
-
\(\dfrac{dy}{dx}=\dfrac{x}{y}\)
- Réponse
-
\(y=\dfrac{5}{3}x−\dfrac{16}{3}\)
Concepts clés
- Nous utilisons la différenciation implicite pour trouver des dérivées de fonctions implicitement définies (fonctions définies par des équations).
- En utilisant la différenciation implicite, nous pouvons trouver l'équation d'une droite tangente au graphe d'une courbe.
Lexique
- différenciation implicite
- est une technique de calcul\(\dfrac{dy}{dx}\) pour une fonction définie par une équation, réalisée en différenciant les deux côtés de l'équation (en n'oubliant pas de traiter la variable\(y\) comme une fonction) et en résolvant\(\dfrac{dy}{dx}\)


