3.8E : Exercices pour la section 3.8

Last updated
Save as PDF

Page ID: 197818

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 10, utilisez la différenciation implicite pour trouver$\dfrac{dy}{dx}$.

1)$x^2−y^2=4$

2)$6x^2+3y^2=12$

Réponse: $\dfrac{dy}{dx}=\dfrac{−2x}{y}$

3)$x^2y=y−7$

4)$3x^3+9xy^2=5x^3$

Réponse: $\dfrac{dy}{dx}=\dfrac{x}{3y}−\dfrac{y}{2x}$

5)$xy−\cos(xy)=1$

6)$y\sqrt{x+4}=xy+8$

Réponse: $\dfrac{dy}{dx}=\dfrac{y−\dfrac{y}{2\sqrt{x+4}}}{\sqrt{x+4}−x}$

7)$−xy−2=\frac{x}{7}$

8)$y\sin(xy)=y^2+2$

Réponse: $\dfrac{dy}{dx}=\dfrac{y^2\cos(xy)}{2y−\sin(xy)−xy\cos(xy)}$

9)$(xy)^2+3x=y^2$

10)$x^3y+xy^3=−8$

Réponse: $\dfrac{dy}{dx}=\dfrac{−3x^2y−y^3}{x^3+3xy^2}$

Pour les exercices 11 à 16, trouvez l'équation de la tangente au graphique de l'équation donnée au point indiqué. Utilisez une calculatrice ou un logiciel pour représenter graphiquement la fonction et la tangente.

11) [T]$x^4y−xy^3=−2, \quad (−1,−1)$

12) [T]$x^2y^2+5xy=14,\quad (2,1)$

Réponse

$y=−\frac{1}{2}x+2$

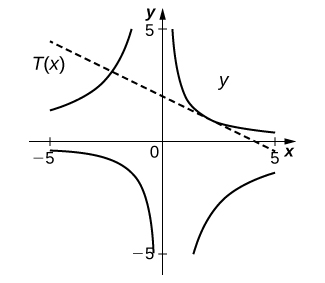
$Le graphique comporte un croissant dans chacun des quatre quadrants. Il existe une droite marquée T (x) avec une pente −1/2 et une intersection y 2.$

13) [T]$\tan(xy)=y,\quad \left(\frac{π}{4},1\right)$

14) [T]$xy^2+\sin(πy)−2x^2=10, \quad (2,−3)$

Réponse

$y=\frac{1}{π+12}x−\frac{3π+38}{π+12}$

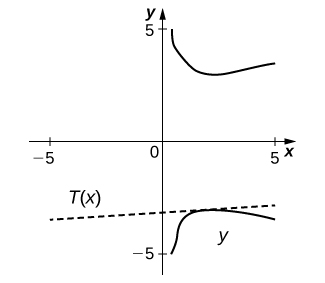
$Le graphique comporte deux courbes, l'une dans le premier quadrant et l'autre dans le quatrième quadrant. Ils sont symétriques par rapport à l'axe X. La courbe du premier quadrant va de (0,3, 5) à (1,5, 3,5) à (5, 4). Il existe une droite marquée T (x) avec une pente 1/ (π + 12) et une intersection y − (3π + 38)/(π + 12).$

15) [T]$\dfrac{x}{y}+5x−7=−\frac{3}{4}y, \quad (1,2)$

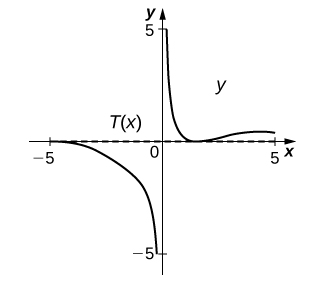
16) [T]$xy+\sin(x)=1,\quad \left(\frac{π}{2},0\right)$

Réponse

$y=0$

$Le graphique commence dans le troisième quadrant proche de (−5, 0), reste proche de 0 jusqu'à ce que x = −4, puis il diminue jusqu'à ce qu'il atteigne près de (0, −5). Il existe une asymptote à x = 0. Le graphique recommence à proximité de (0, 5), diminue jusqu'à (1, 0), puis augmente légèrement avant de diminuer pour être proche (5, 0). Il existe une ligne droite marquée T (x) qui coïncide avec y = 0.$

17) [T] Le graphique d'un folium de Descartes avec équation$2x^3+2y^3−9xy=0$ est donné dans le graphique suivant.

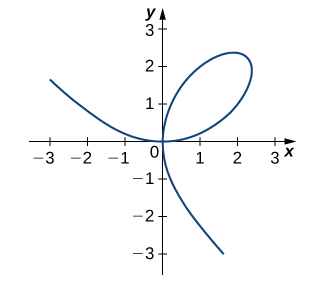
$Un folium est représenté graphiquement avec l'équation 2x3 + 2y3 — 9xy = 0. Il se croise à (0, 0).$

a. Trouvez l'équation de la tangente au point$(2,1)$. Tracez la tangente avec le feuillet.

b. Trouvez l'équation de la droite normale à la tangente dans a. au point$(2,1)$.

18) Pour l'équation$x^2+2xy−3y^2=0,$

a. Trouvez l'équation de la normale à la tangente au point$(1,1)$.

b. À quel autre point la droite normale du point a. croise le graphique de l'équation ?

Réponse: a.$y=−x+2$
b.$(3,−1)$

19) Trouvez tous les points du$y^3−27y=x^2−90$ graphique auxquels la tangente est verticale.

20) Pour l'équation$x^2+xy+y^2=7$,

a. Trouvez le ou les$x$ -intercept (s).

b.Détermine la pente de la ou des tangentes à l'$x$intersection (s).

c. Qu'est-ce que la ou les valeurs de la partie b. indiquent à propos de la ou des lignes tangentes ?

Réponse: a.$\left(±\sqrt{7},0\right)$
b.$−2$
c. Ils sont parallèles puisque la pente est la même aux deux intersections.

21) Trouvez l'équation de la tangente au graphe de l'équation$\sin^{−1}x+\sin^{−1}y=\frac{π}{6}$ au point$\left(0,\frac{1}{2}\right)$.

22) Trouvez l'équation de la tangente au graphe de l'équation$\tan^{−1}(x+y)=x^2+\frac{π}{4}$ au point$(0,1)$.

Réponse: $y=−x+1$

23) Trouver$y′$ et$y''$ pour$x^2+6xy−2y^2=3$.

24) [T] Le nombre de téléphones portables produits lorsque des$x$ dollars sont dépensés en main-d'œuvre et des$y$ dollars en capital investi par un fabricant peut être modélisé par l'équation$60x^{3/4}y^{1/4}=3240$.

a. Trouvez$\frac{dy}{dx}$ et évaluez sur le point$(81,16)$.

b. Interpréter le résultat d'un.

Réponse: a.$\frac{dy}{dx}=−0.5926$
b. Lorsque 81 dollars sont dépensés en main-d'œuvre et 16 dollars en capital, le montant dépensé en capital diminue de 0,5926$ par dollar dépensé en main-d'œuvre.

25) [T] Le nombre de voitures produites lorsque des$x$ dollars sont dépensés en main-d'œuvre et des$y$ dollars en capital investi par un constructeur peut être modélisé par l'équation$30x^{1/3}y^{2/3}=360$.

(Les deux$x$$y$ sont mesurés en milliers de dollars.)

a. Trouvez$\frac{dy}{dx}$ et évaluez sur le point$(27,8)$.

b. Interpréter le résultat de la partie a.

26) Le volume d'un cône circulaire droit de rayon$x$ et de hauteur$y$ est donné par$V=\frac{1}{3}πx^2y$. Supposons que le volume du cône soit$85π\,\text{cm}^3$. Trouvez$\dfrac{dy}{dx}$ quand$x=4$ et$y=16$.

Réponse: $\dfrac{dy}{dx} = −8$

Pour les exercices 27 à 28, considérez une boîte rectangulaire fermée avec une base carrée avec côté$x$ et hauteur$y$.

27) Trouvez une équation pour la surface de la boîte rectangulaire,$S(x,y)$.

28) Si la surface de la boîte rectangulaire est de 78 pieds carrés, déterminez$\dfrac{dy}{dx}$ quand$x=3$ pieds et$y=5$ pieds.

Réponse: $\dfrac{dy}{dx} = −2.67$

Dans les exercices 29 à 31, utilisez la différenciation implicite pour déterminer$y′$. La réponse correspond-elle aux formules que nous avons déterminées précédemment ?

29)$x=\sin y$

30)$x=\cos y$

Réponse: $y′=−\dfrac{1}{\sqrt{1−x^2}}$

31)$x=\tan y$