3.7E : Exercices pour la section 3.7

Last updated
Save as PDF

Page ID: 197767

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, utilisez le graphique$y=f(x)$ de

a. esquissez le graphique de$y=f^{−1}(x)$, et

b. utilisez la partie a. pour effectuer une estimation$\big(f^{−1}\big)′(1)$.

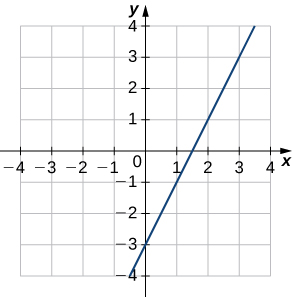
$Une droite passant par (0, -3) et (3, 3).$

$Une ligne courbe commençant à (−2, 0) et passant par (-1, 1) et (2, 2).$

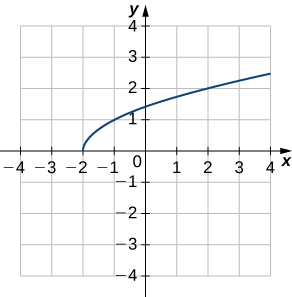
Réponse

un.

$alt$

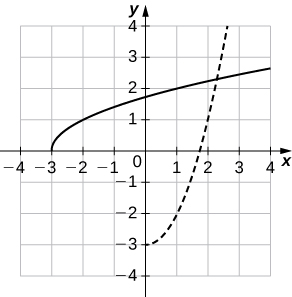
b.$(f^{−1})′(1)\approx 2$

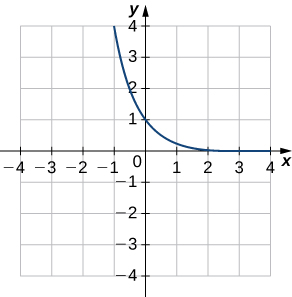
$Une ligne courbe commençant à (4, 0) et passant par (0, 1) et (−1, 4).$

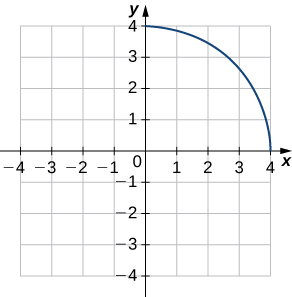
$Un quart de cercle commençant à (0, 4) et se terminant à (4, 0).$

Réponse

un.

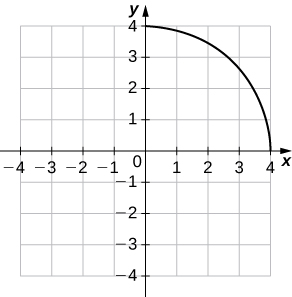
$Un quart de cercle commençant à (0, 4) et se terminant à (4, 0).$

b.$(f^{−1})′(1)\approx −1/\sqrt{3}$

Pour les exercices 5 à 8, utilisez la fonction donnée$y=f(x)$ pour trouver

a.$\dfrac{df}{dx}$ à$x=a$ et

$x=f^{−1}(y)$b.

c. Utilisez ensuite la partie b. pour trouver$\dfrac{df^{−1}}{dy}$$y=f(a).$

5)$f(x)=6x−1,\; x=−2$

6)$f(x)=2x^3−3,\; x=1$

Réponse: a.$\dfrac{df}{dx} = 6$
b.$x=f^{−1}(y)=\left(\dfrac{y+3}{2}\right)^{1/3}$
c.$\dfrac{df^{−1}}{dy} = \frac{1}{6}$

7)$f(x)=9−x^2,\; 0≤x≤3,x=2$

8)$f(x)=\sin x,\; x=0$

Réponse: a.$\dfrac{df}{dx} = 1$
b.$x=f^{−1}(y)=\sin^{−1}y$
c.$\dfrac{df^{−1}}{dy} = 1$

Pour chaque fonction des exercices 9 à 14, trouvez$\big(f^{−1}\big)′(a)$.

9)$f(x)=x^2+3x+2,\; x≥−1,\; a=2$

10$f(x)=x^3+2x+3,\; a=0$

Réponse: $\big(f^{−1}\big)′(1) = \frac{1}{5}$

11)$f(x)=x+\sqrt{x},\; a=2$

(12)$f(x)=x−\frac{2}{x},\; x<0,\; a=1$

Réponse: $\big(f^{−1}\big)′(1) = \frac{1}{3}$

13)$f(x)=x+\sin x,\; a=0$

(14)$f(x)=\tan x+3x^2,\; a=0$

Réponse: $\big(f^{−1}\big)′(0) = 1$

Pour chaque fonction$y=f(x)$, donnée dans les exercices 15 à 19,

a. déterminer la pente de la tangente par rapport à sa fonction inverse$f^{−1}$ au point indiqué$P$, et

b. trouve l'équation de la tangente au graphe de$f^{−1}$ au point indiqué.

15)$f(x)=\dfrac{4}{1+x^2},\quad P(2,1)$

16)$f(x)=\sqrt{x−4},\quad P(2,8)$

Réponse: a.$4$
b.$y=4x$

17)$f(x)=(x^3+1)^4,\quad P(16,1)$

18)$f(x)=−x^3−x+2,\quad P(−8,2)$

Réponse: a.$−\frac{1}{96}$
b.$y=−\frac{1}{13}x+\frac{18}{13}$

19)$f(x)=x^5+3x^3−4x−8,\quad P(−8,1)$

Dans les exercices 20 à 29,$\dfrac{dy}{dx}$ recherchez la fonction donnée.

20)$y=\sin^{−1}(x^2)$

Réponse: $\dfrac{dy}{dx} = \dfrac{2x}{\sqrt{1−x^4}}$

(21)$y=\cos^{−1}\left(\sqrt{x}\right)$

22)$y=\sec^{−1}\left(\frac{1}{x}\right)$

Réponse: $\dfrac{dy}{dx} = \dfrac{−1}{\sqrt{1−x^2}}$

23)$y=\sqrt{\csc^{−1}x}$

(24)$y=(1+\tan^{−1}x)^3$

Réponse: $\dfrac{dy}{dx} = \dfrac{3(1+\tan^{−1}x)^2}{1+x^2}$

25)$y=\cos^{−1}(2x)⋅\sin^{−1}(2x)$

26)$y=\dfrac{1}{\tan^{−1}(x)}$

Réponse: $\dfrac{dy}{dx} = \dfrac{−1}{(1+x^2)(\tan^{−1}x)^2}$

(27)$y=\sec^{−1}(−x)$

28)$y=\cot^{−1}\sqrt{4−x^2}$

Réponse: $\dfrac{dy}{dx} = \dfrac{x}{(5−x^2)\sqrt{4−x^2}}$

(29)$y=x⋅\csc^{−1}x$

Dans les exercices 30 à 35, utilisez les valeurs données pour trouver$\big(f^{−1}\big)′(a)$.

30)$f(π)=0,f'(π)=−1,a=0$

Réponse: $\big(f^{−1}\big)′(0) = −1$

31)$f(6)=2,\; f′(6)=\frac{1}{3},\; a=2$

32)$f(\frac{1}{3})=−8,\; f'(\frac{1}{3})=2,\; a=−8$

Réponse: $\big(f^{−1}\big)′(-8) = \frac{1}{2}$

33)$f(\sqrt{3})=\frac{1}{2},f'(\sqrt{3})=\frac{2}{3},a=\frac{1}{2}$

34)$f(1)=−3,\; f'(1)=10,\; a=−3$

Réponse: $\big(f^{−1}\big)′(-3) =\frac{1}{10}$

35)$f(1)=0,\; f'(1)=−2,\; a=0$

36) [T] La position d'une rondelle de hockey en mouvement après$t$ quelques secondes$s(t)=tan^{−1}t$$s$ est exprimée en mètres.

a. Déterminez la vitesse de la rondelle de hockey à tout moment$t$.

b. Trouvez l'accélération de la rondelle à tout moment$t$.

c. Évaluez les parties a. et b. pendant$t=2,\, 4$ et en$6$ secondes.

d. Quelle conclusion peut-on tirer des résultats de la section c. ?

Réponse

a.$v(t)=\dfrac{1}{1+t^2}$
b.$a(t)=\dfrac{−2t}{(1+t^2)^2}$
c. (a)$0.2,\, 0.06,\, 0.03$ ; (b)$−0.16,\, −0.028,\, −0.0088$

d. La rondelle de hockey ralentit ou ralentit au bout de 2, 4 et 6 secondes.

Solution :

37) [T] Un bâtiment de 225 pieds de haut projette une ombre de différentes longueurs$x$ au fil de la journée. Un angle d'élévation$θ$ est formé par des lignes allant du haut et du bas du bâtiment jusqu'à la pointe de l'ombre, comme le montre la figure suivante. Détermine le taux de variation de l'angle d'élévation$\frac{dθ}{dx}$ en$x=272$ pieds.

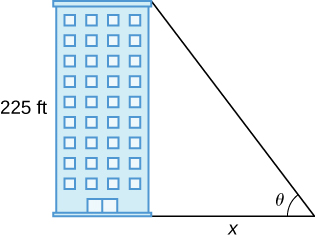
$Un bâtiment est représenté avec une hauteur de 225 pieds. Un triangle est formé avec la hauteur du bâtiment comme côté opposé à l'angle θ. Le côté adjacent a une longueur x.$

38) [T] Un mât mesure 75 pieds de haut. Un angle$θ$ se forme lorsque des fils de différentes longueurs de$x$ pieds sont attachés du sol au sommet du poteau, comme le montre la figure suivante. Déterminez le taux de variation de l'angle$\frac{dθ}{dx}$ lorsqu'un fil de 90 pieds de long est attaché.

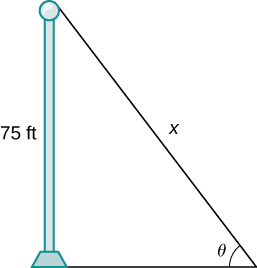
$Un mât de drapeau est représenté avec une hauteur de 75 pieds. Un triangle est formé avec la hauteur du mât comme côté opposé à l'angle θ. L'hypoténuse a une longueur x.$

Réponse: $−0.0168$radians par pied

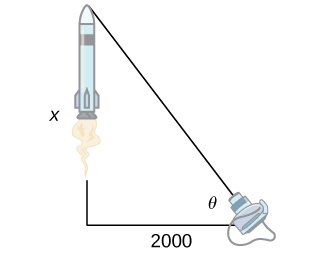
39) [T] Une caméra de télévision au niveau du sol se trouve à 2000 pieds de la rampe de lancement d'une fusée spatiale qui doit décoller verticalement, comme le montre la figure suivante. L'angle d'élévation de la caméra peut être déterminé par$θ=\tan^{−1}\left(\frac{x}{2000}\right)$, où$x$ est la hauteur de la fusée. Déterminez le taux de variation de l'angle d'élévation après le lancement lorsque la caméra et la fusée sont distantes de 5 000 pieds.

$Une fusée est représentée en l'air, la distance entre son nez et le sol étant de x. Un triangle est formé avec la hauteur de la fusée comme le côté opposé à l'angle θ. Le côté adjacent a une longueur de 2000.$

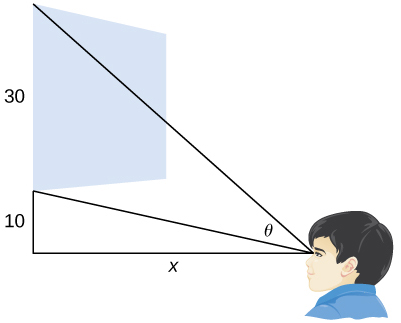
40) [T] Un cinéma local avec un écran de 30 pieds de haut situé à 10 pieds au-dessus du niveau des yeux d'une personne assise a un angle de vision$θ$ (en radians) donné par$θ=\cot^{−1}\frac{x}{40}−\cot^{−1}\frac{x}{10}$ :

où$x$ est la distance en pieds de l'écran de cinéma où la personne est assise, comme le montre la figure suivante.

$Une personne est représentée avec un triangle droit venant de l'œil (l'angle droit étant du côté opposé à l'œil), avec une hauteur de 10 et une base x. Une ligne est tracée entre l'œil et le haut de l'écran, qui forme un angle θ avec l'hypoténuse du triangle. L'écran a une hauteur de 30.$

a. Trouvez$\dfrac{dθ}{dx}$.

b. Évaluez$\dfrac{dθ}{dx}$ pour$x=5,\,10,\,15,$ et$20$.

c. Interpréter les résultats de la partie b.

d. Évaluer$\dfrac{dθ}{dx}$ pour$x=25,\,30,\,35$, et$40$.

e. Interpréter les résultats dans la partie d. À quelle distance la personne$x$ doit-elle se tenir pour maximiser son angle de vision ?

Réponse: a.$\dfrac{dθ}{dx}=\dfrac{10}{100+x^2}−\dfrac{40}{1600+x^2}$
b.$\frac{18}{325},\,\frac{9}{340},\,\frac{42}{4745},\,0$
c. À mesure qu'une personne s'éloigne de l'écran, l'angle de vision augmente, ce qui signifie qu'à mesure qu'elle s'éloigne, sa vision de l'écran s'élargit. d.$−\frac{54}{12905},\,−\frac{3}{500},\,−\frac{198}{29945},\,−\frac{9}{1360}$
e. Lorsque la personne se déplace au-delà de 20 pieds à partir de l'écran, l'angle de vision diminue. La distance optimale à laquelle la personne doit se tenir pour maximiser l'angle de vision est de 20 pieds.