3.5 : Dérivées des fonctions trigonométriques
- Page ID
- 197766
- Déterminez les dérivées des fonctions sinus et cosinus.
- Trouvez les dérivées des fonctions trigonométriques standard.
- Calculez les dérivées d'ordre supérieur du sinus et du cosinus.
L'un des types de mouvement les plus importants en physique est le mouvement harmonique simple, associé à des systèmes tels qu'un objet dont la masse oscille sur un ressort. Un mouvement harmonique simple peut être décrit en utilisant des fonctions sinusoïdales ou cosinusoïdales. Dans cette section, nous élargissons nos connaissances sur les formules dérivées pour inclure les dérivées de ces fonctions et d'autres fonctions trigonométriques. Nous commençons par les dérivées des fonctions sinus et cosinus, puis nous les utilisons pour obtenir des formules pour les dérivées des quatre fonctions trigonométriques restantes. Le fait de pouvoir calculer les dérivées des fonctions sinus et cosinus nous permettra de déterminer la vitesse et l'accélération d'un mouvement harmonique simple.
Dérivés des fonctions sinus et cosinus
Nous commençons notre exploration de la dérivée de la fonction sinusoïdale en utilisant la formule pour faire une estimation raisonnable de sa dérivée. Rappelez-vous que pour une fonction\(f(x),\)
\[f′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Par conséquent, pour des valeurs\(h\) très proches de\(0\),
\[f′(x)≈\dfrac{f(x+h)−f(x)}{h}. \nonumber \]
Nous constatons qu'en utilisant\(h=0.01\),
\[\dfrac{d}{dx}(\sin x)≈\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
En réglant
\[D(x)=\dfrac{\sin (x+0.01)−\sin x}{0.01} \nonumber \]
et à l'aide d'un utilitaire graphique, nous pouvons obtenir un graphique d'une approximation de la dérivée de\(\sin x\) (Figure\(\PageIndex{1}\)).
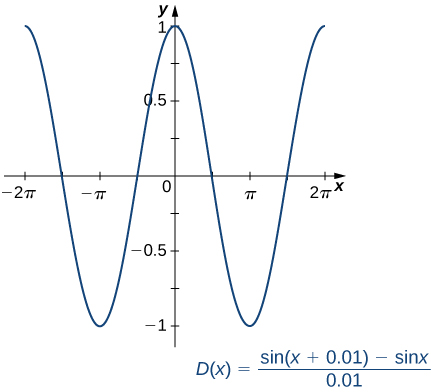
À l'inspection, le graphe de\(D(x)\) semble être très proche du graphe de la fonction cosinus. En effet, nous allons montrer que
\[\dfrac{d}{dx}(\sin x)=\cos x. \nonumber \]
Si nous devions suivre les mêmes étapes pour approximer la dérivée de la fonction cosinus, nous trouverions que
\[\dfrac{d}{dx}(\cos x)=−\sin x. \nonumber \]
La dérivée de la fonction sinusoïdale est le cosinus et la dérivée de la fonction cosinus est le sinus négatif.
\[\dfrac{d}{dx}(\sin x)=\cos x \nonumber \]
\[\dfrac{d}{dx}(\cos x)=−\sin x \nonumber \]
Parce que les preuves\(\dfrac{d}{dx}(\sin x)=\cos x\) et\(\dfrac{d}{dx}(\cos x)=−\sin x\) utilisent des techniques similaires, nous ne fournissons que les preuves pour\(\dfrac{d}{dx}(\sin x)=\cos x\). Avant de commencer, rappelez-vous deux limites trigonométriques importantes :
\(\displaystyle \lim_{h→0}\dfrac{\sin h}{h}=1\)et\(\displaystyle \lim_{h→0}\dfrac{\cos h−1}{h}=0\).
Les graphiques de\(y=\dfrac{\sin h}{h}\) et\(y=\dfrac{\cos h−1}{h}\) sont présentés dans la figure\(\PageIndex{2}\).
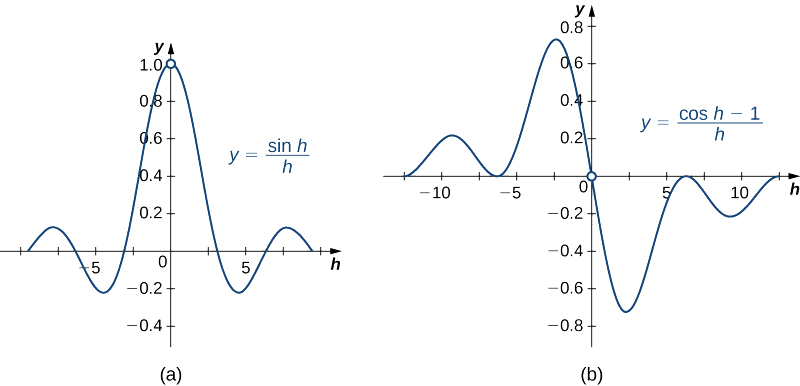
Nous rappelons également l'identité trigonométrique suivante pour le sinus de la somme de deux angles :
\[\sin (x+h)=\sin x\cos h+\cos x\sin h. \nonumber \]
Maintenant que nous avons rassemblé toutes les équations et identités nécessaires, nous procédons à la preuve.
\ [\ begin {align*} \ dfrac {d} {dx} (\ sin x) &= \ lim_ {h→0} \ dfrac {\ sin (x+h) − \ sin x} {h} & & \ text {Appliquez la définition de la dérivée.} \ \ [4pt]
&= \ lim_ {h→0} \ dfrac {\ sin x \ cos h+} \ cos x \ sin h− \ sin x} {h} & & \ text {Utilisez l'identité trig pour le sinus de la somme de deux angles.} \ \ [4pt]
&= \ lim_ {h→0} \ left (\ dfrac {\ sin x \ cos h− \ sin x} {h} + \ dfrac {\ cos x \ sin h} {h} \ right) & \ text {Regrouper.} \ \ [4 points]
&= \ lim_ {h→0} \ left (\ sin x \ left (\ dfrac {\ cos h−1]} {h} \ right) + (\ cos x) \ left (\ dfrac {\ sin h} {h} \ right) \ right) & \ text {Factor out} \ sin x \ text {et} \ cos x \ \ [4pt]
& =( \ sin x) \ lim_ {h→0} \ left (\ dfrac {\ cos h−1} {h} \ right) + (\ cos x) \ lim_ {h→0} \ left (\ dfrac {\ sin h} {h} \ right) & \ text {Factor} \ sin x \ text {hors limites.} \ \ [4pt]
& =( \ sin x) (0) + (\ cos x) (1) & \ text {Appliquer des formules de limite de trig.} \ \ [4 points]
&= \ cos x & & \ text {Simplifier.} \ end {align*} \ nonumber \]
□
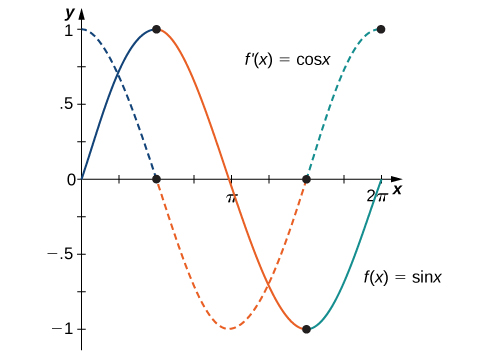
La figure\(\PageIndex{3}\) montre la relation entre le graphe de\(f(x)=\sin x\) et sa dérivée\(f′(x)=\cos x\). Remarquez qu'aux points où\(f(x)=\sin x\) a une tangente horizontale, sa dérivée\(f′(x)=\cos x\) prend la valeur zéro. Nous voyons également que lorsque f\((x)=\sin x\) augmente\(f′(x)=\cos x>0\) et où\(f(x)=\sin x\) diminue,\(f′(x)=\cos x<0.\)
Trouvez la dérivée de\(f(x)=5x^3\sin x\).
Solution
En utilisant la règle du produit, nous avons
\[ \begin{align*} f'(x) &=\dfrac{d}{dx}(5x^3)⋅\sin x+\dfrac{d}{dx}(\sin x)⋅5x^3 \\[4pt] &=15x^2⋅\sin x+\cos x⋅5x^3. \end{align*}\]
Après avoir simplifié, nous obtenons
\[f′(x)=15x^2\sin x+5x^3\cos x. \nonumber \]
Trouvez la dérivée de\(f(x)=\sin x\cos x.\)
- Allusion
-
N'oubliez pas d'utiliser la règle du produit.
- Réponse
-
\[f′(x)=\cos^2x−\sin^2x \nonumber \]
Trouvez la dérivée de\(g(x)=\dfrac{\cos x}{4x^2}\).
Solution
En appliquant la règle du quotient, nous avons
\[g′(x)=\dfrac{(−\sin x)4x^2−8x(\cos x)}{(4x^2)^2}. \nonumber \]
En simplifiant, nous obtenons
\[g′(x)=\dfrac{−4x^2\sin x−8x\cos x}{16x^4}=\dfrac{−x\sin x−2\cos x}{4x^3}. \nonumber \]
Trouvez la dérivée de\(f(x)=\dfrac{x}{\cos x}\).
- Allusion
-
Utilisez la règle du quotient.
- Réponse
-
\(f'(x) = \dfrac{\cos x+x\sin x}{\cos^2x}\)
Une particule se déplace le long d'un axe de coordonnées de telle sorte que sa position temporelle\(t\) soit donnée par\(0≤t≤2π.\) A\(s(t)=2\sin t−t\) à quelles heures la particule est-elle au repos ?
Solution
Pour déterminer quand la particule est au repos, définissez\(s′(t)=v(t)=0.\) Commencer par trouver\(s′(t).\) Nous obtenons
\[s′(t)=2 \cos t−1, \nonumber \]
nous devons donc résoudre
\[2 \cos t−1=0\text{ for }0≤t≤2π. \nonumber \]
Les solutions à cette équation sont\(t=\dfrac{π}{3}\) et\(t=\dfrac{5π}{3}\). Ainsi, la particule est au repos de temps en temps\(t=\dfrac{π}{3}\) et\(t=\dfrac{5π}{3}\).
Une particule se déplace le long d'un axe de coordonnées. Sa position dans le temps\(t\) est donnée par\(s(t)=\sqrt{3}t+2\cos t\) pour\(0≤t≤2π.\) À quelles heures la particule est-elle au repos ?
- Allusion
-
Utilisez l'exemple précédent comme guide.
- Réponse
-
\(t=\dfrac{π}{3},\quad t=\dfrac{2π}{3}\)
Dérivés d'autres fonctions trigonométriques
Comme les quatre fonctions trigonométriques restantes peuvent être exprimées sous forme de quotients impliquant un sinus, un cosinus ou les deux, nous pouvons utiliser la règle du quotient pour trouver des formules pour leurs dérivées.
Trouvez la dérivée de\(f(x)=\tan x.\)
Solution
Commencez par exprimer\(\tan x \) comme le quotient de\(\sin x\) et\(\cos x\) :
\(f(x)=\tan x =\dfrac{\sin x}{\cos x}\).
Appliquez maintenant la règle du quotient pour obtenir
\(f′(x)=\dfrac{\cos x\cos x−(−\sin x)\sin x}{(\cos x)^2}\).
En simplifiant, nous obtenons
\[f′(x)=\dfrac{\cos^2x+\sin^2 x}{\cos^2x}. \nonumber \]
Reconnaissant que,\(\cos^2x+\sin^2x=1,\) selon le théorème de Pythagore, nous avons maintenant
\[f′(x)=\dfrac{1}{\cos^2x} \nonumber \]
Enfin, utilisez l'identité\(\sec x=\dfrac{1}{\cos x}\) pour obtenir
\(f′(x)=\text{sec}^2 x\).
Trouvez la dérivée de\(f(x)=\cot x .\)
- Allusion
-
Réécrivez\(\cot x \) comme\(\dfrac{\cos x}{\sin x}\) et utilisez la règle du quotient.
- Réponse
-
\(f′(x)=−\csc^2 x\)
Les dérivés des fonctions trigonométriques restantes peuvent être obtenus en utilisant des techniques similaires. Nous fournissons ces formules dans le théorème suivant.
Les dérivées des fonctions trigonométriques restantes sont les suivantes :
\ [\ begin {align} \ dfrac {d} {dx} (\ tan x) &= \ sec^2x \ \ [4 points]
\ dfrac {d} {dx} (\ cot x) &=− \ csc^2x \ \ [4 points]
\ dfrac {d} {dx} (\ sec x) &= \ sec x \ tan x \ \ [4 points]
\ dfrac {d} {dx} (\ csc x) &=− \ csc x \ cot x. \ end {align} \ nonumber \]
Détermine l'équation d'une droite tangente au graphe de\(f(x)=\cot x \) at\(x=\frac{π}{4}\).
Solution
Pour trouver l'équation de la tangente, nous avons besoin d'un point et d'une pente à ce point. Pour trouver le point, calculez
\(f\left(\frac{π}{4}\right)=\cot\frac{π}{4}=1\).
Ainsi, la tangente passe par le point\(\left(\frac{π}{4},1\right)\). Ensuite, déterminez la pente en trouvant la dérivée de\(f(x)=\cot x \) et en l'évaluant comme\(\frac{π}{4}\) suit :
\(f′(x)=−\csc^2 x\)et\(f′\left(\frac{π}{4}\right)=−\csc^2\left(\frac{π}{4}\right)=−2\).
En utilisant l'équation de pente ponctuelle de la droite, nous obtenons
\(y−1=−2\left(x−\frac{π}{4}\right)\)
ou de manière équivalente,
\(y=−2x+1+\frac{π}{2}\).
Trouvez la dérivée de\(f(x)=\csc x+x\tan x .\)
Solution
Pour trouver cette dérivée, nous devons utiliser à la fois la règle de la somme et la règle du produit. En utilisant la règle de la somme, nous trouvons
\(f′(x)=\dfrac{d}{dx}(\csc x)+\dfrac{d}{dx}(x\tan x )\).
Au premier terme,\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x ,\) et en appliquant la règle du produit au second terme, nous obtenons
\(\dfrac{d}{dx}(x\tan x )=(1)(\tan x )+(\sec^2 x)(x)\).
Par conséquent, nous avons
\(f′(x)=−\csc x\cot x +\tan x +x\sec^2 x\).
Trouvez la dérivée de\(f(x)=2\tan x −3\cot x .\)
- Allusion
-
Utilisez la règle pour différencier un multiple constant et la règle pour différencier une différence entre deux fonctions.
- Réponse
-
\(f′(x)=2\sec^2 x+3\csc^2 x\)
Détermine la pente de la droite tangente au graphe de\(f(x)=\tan x \) at\(x=\dfrac{π}{6}\).
- Allusion
-
Évaluez la dérivée à\(x=\dfrac{π}{6}\).
- Réponse
-
\(\dfrac{4}{3}\)
Produits dérivés d'ordre supérieur
Les dérivées d'ordre supérieur de\(\sin x\) et\(\cos x\) suivent un schéma répétitif. En suivant le modèle, nous pouvons trouver n'importe quelle dérivée d'ordre supérieur de\(\sin x\) et\(\cos x.\)
Découvrez les quatre premiers dérivés de\(y=\sin x.\)
Solution
Chaque étape de la chaîne est simple :
\ [\ begin {align*} y&= \ sin x \ \ [4 points]
\ dfrac {dy} {dx} &= \ cos x \ \ [4 points] \ dfrac {d^2y} {dx^2} &=−
\ sin x \ \ [4 points] \ dfrac {d^3y} {dx^3} &=−
\ cos x \ \ [4 points] \ dfrac {d^3y} {dx^3} &=− \ cos x
\ \ [4 points]] \ dfrac {d^4y} {dx^4} &= \ sin x \ end {align*} \]
Analyse
Une fois que nous avons reconnu le modèle des dérivées, nous pouvons trouver n'importe quelle dérivée d'ordre supérieur en déterminant l'étape du modèle à laquelle elle correspond. Par exemple, une dérivée sur quatre de\(\sin x\) vaut\(\sin x\), donc
\[\dfrac{d^4}{dx^4}(\sin x)=\dfrac{d^8}{dx^8}(\sin x)=\dfrac{d^{12}}{dx^{12}}(\sin x)=…=\dfrac{d^{4n}}{dx^{4n}}(\sin x)=\sin x \nonumber \]
\[\dfrac{d^5}{dx^5}(\sin x)=\dfrac{d^9}{dx^9}(\sin x)=\dfrac{d^{13}}{dx^{13}}(\sin x)=…=\dfrac{d^{4n+1}}{dx^{4n+1}}(\sin x)=\cos x. \nonumber \]
Pour\(y=\cos x\), trouvez\(\dfrac{d^4y}{dx^4}\).
- Allusion
-
Reportez-vous à l'exemple précédent.
- Réponse
-
\(\cos x\)
Trouvez\(\dfrac{d^{74}}{dx^{74}}(\sin x)\).
Solution
Nous pouvons voir tout de suite que pour la dérivée 74e de\(\sin x\)\(74=4(18)+2\), donc
\[\dfrac{d^{74}}{dx^{74}}(\sin x)=\dfrac{d^{72+2}}{dx^{72+2}}(\sin x)=\dfrac{d^2}{dx^2}(\sin x)=−\sin x. \nonumber \]
Pour\(y=\sin x\), trouvez\(\dfrac{d^{59}}{dx^{59}}(\sin x).\)
- Allusion
-
\(\dfrac{d^{59}}{dx^{59}}(\sin x)=\dfrac{d^{4⋅14+3}}{dx^{4⋅14+3}}(\sin x)\)
- Réponse
-
\(−\cos x\)
Une particule se déplace le long d'un axe de coordonnées de telle sorte que sa position temporelle\(t\) soit donnée par\(s(t)=2−\sin t\). Trouvez\(v(π/4)\) et\(a(π/4)\). Comparez ces valeurs et déterminez si la particule accélère ou ralentit.
Solution
Première découverte\(v(t)=s′(t)\)
\[v(t)=s′(t)=−\cos t . \nonumber \]
Ainsi,
\(v\left(\frac{π}{4}\right)=−\dfrac{1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\).
Ensuite, trouvez\(a(t)=v′(t)\). Ainsi,\(a(t)=v′(t)=\sin t\) et nous avons
\(a\left(\frac{π}{4}\right)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\).
Depuis\(v\left(\frac{π}{4}\right)=−\dfrac{\sqrt{2}}{2}<0\) et\(a\left(\frac{π}{4}\right)=\dfrac{\sqrt{2}}{2}>0\), nous voyons que la vitesse et l'accélération agissent dans des directions opposées, c'est-à-dire que l'objet est accéléré dans la direction opposée à la direction dans laquelle il se déplace. Par conséquent, la particule ralentit.
Un bloc fixé à un ressort se déplace verticalement. Sa position à l'instant t est donnée par\(s(t)=2\sin t\). Trouvez\(v\left(\frac{5π}{6}\right)\) et\(a\left(\frac{5π}{6}\right)\). Comparez ces valeurs et déterminez si le bloc accélère ou ralentit.
- Allusion
-
Utilisez Example\(\PageIndex{9}\) comme guide.
- Réponse
-
\(v\left(\frac{5π}{6}\right)=−\sqrt{3}<0\)et\(a\left(\frac{5π}{6}\right)=−1<0\). Le bloc s'accélère.
Concepts clés
- Nous pouvons trouver les dérivées de\(\sin x\) et\(\cos x\) en utilisant la définition de la dérivée et les formules limites trouvées précédemment. Les résultats sont
\(\dfrac{d}{dx}\big(\sin x\big)=\cos x\quad\text{and}\quad\dfrac{d}{dx}\big(\cos x\big)=−\sin x\).
- Avec ces deux formules, nous pouvons déterminer les dérivées des six fonctions trigonométriques de base.
Équations clés
- Dérivé de la fonction sinus
\(\dfrac{d}{dx}(\sin x)=\cos x\)
- Dérivé de la fonction cosinus
\(\dfrac{d}{dx}(\cos x)=−\sin x\)
- Dérivée de la fonction tangente
\(\dfrac{d}{dx}(\tan x )=\sec^2x\)
- Dérivée de la fonction cotangente
\(\dfrac{d}{dx}(\cot x )=−\csc^2x\)
- Dérivé de la fonction sécante
\(\dfrac{d}{dx}(\sec x)=\sec x\tan x \)
- Dérivé de la fonction cosécante
\(\dfrac{d}{dx}(\csc x)=−\csc x\cot x \)


