3.4E : Exercices pour la section 3.4
- Page ID
- 197823
Dans les exercices 1 à 3, les fonctions données représentent la position d'une particule se déplaçant le long d'une ligne horizontale.
a. Trouvez les fonctions de vitesse et d'accélération.
b. Déterminez les intervalles de temps pendant lesquels l'objet ralentit ou accélère.
1)\(s(t)=2t^3−3t^2−12t+8\)
2)\(s(t)=2t^3−15t^2+36t−10\)
- Réponse
- a.\(v(t)=6t^2−30t+36,\quad a(t)=12t−30\) ;
b. accélère pendant\( (2,2.5)∪(3,∞)\), ralentit pendant\((0,2)∪(2.5,3)\)
3)\(s(t)=\dfrac{t}{1+t^2}\)
4) Une roquette est tirée verticalement vers le haut depuis le sol. La distance\(s\) en pieds que la fusée parcourt depuis le sol après\(t\) quelques secondes est donnée par\(s(t)=−16t^2+560t\).
a. Déterminez la vitesse de la fusée 3 secondes après le tir.
b. Trouvez l'accélération de la fusée 3 secondes après le tir.
- Réponse
- a.\(464\; \text{ft/s}^2\)
b.\(−32\;\text{ft/s}^2\)
5) Une balle est lancée vers le bas à une vitesse de 8 pieds/s depuis le haut d'un bâtiment de 64 pieds de haut. Après\(t\) quelques secondes, sa hauteur au-dessus du sol est donnée par\(s(t)=−16t^2−8t+64.\)
a. Déterminez le temps qu'il faut à la balle pour toucher le sol.
b. Déterminez la vitesse de la balle lorsqu'elle touche le sol.
6) La fonction de position\(s(t)=t^2−3t−4\) représente la position de l'arrière d'une voiture qui sort d'une allée puis roule en ligne droite\(s\), en pieds et\(t\) en secondes. Dans ce cas,\(s(t)=0\) représente l'heure à laquelle l'arrière de la voiture se trouve devant la porte du garage, de même que\(s(0)=−4\) la position de départ de la voiture, à 4 pieds à l'intérieur du garage.
a. Déterminez la vitesse de la voiture à quel moment\(s(t)=0\).
b. Déterminez la vitesse de la voiture à quel moment\(s(t)=14\).
- Réponse
- a.\(5\) pieds/s
b.\(9\) pieds/s
7) La position d'un colibri volant le long d'une ligne droite en\(t\) secondes est donnée en\(s(t)=3t^3−7t\) mètres.
a. Déterminez la vitesse de l'oiseau à la\(t=1\) seconde
b. Déterminez l'accélération de l'oiseau à la\(t=1\) seconde
c. Déterminez l'accélération de l'oiseau lorsque la vitesse est égale à 0.
8) Une pomme de terre est lancée verticalement vers le haut avec une vitesse initiale de 100 pieds/s à partir d'un pistolet à pommes de terre situé au sommet d'un bâtiment de 85 pieds de haut. La distance en pieds que la pomme de terre parcourt depuis le sol après\(t\) quelques secondes est donnée par\(s(t)=−16t^2+100t+85\).
a. Détermine la vitesse de la pomme de terre après\(0.5\)\(5.75\) s et s.
b. Détermine la vitesse de la pomme de terre\(0.5\) en\(5.75\) s et s.
c. Déterminez le moment où la pomme de terre atteint sa hauteur maximale.
d. Détermine l'accélération de la pomme de terre\(0.5\) en\(1.5\) s et s.
e. Déterminez combien de temps la pomme de terre reste dans l'air.
f. Déterminez la vitesse de la pomme de terre lorsqu'elle touche le sol.
- Réponse
- a. 84 ft/s, −84 ft/s
b. 84 ft/s
c.\(\frac{25}{8}\) s
d.\(−32 \; \text{ft/s}^2\) dans les deux cas
e.\(\frac{1}{8}(25+\sqrt{965})\) s
f.\(−4\sqrt{965}\) ft/s
9) La fonction de position\(s(t)=t^3−8t\) donne la position en miles d'un train de marchandises, l'est étant la direction positive et\(t\) est mesurée en heures.
a. Déterminez la direction dans laquelle le train se déplace\(s(t)=0\).
b. Déterminez la direction dans laquelle se déplace le train\(a(t)=0\).
c. Déterminez les intervalles de temps pendant lesquels le train ralentit ou accélère.
10) Le graphique suivant montre la position\(y=s(t)\) d'un objet se déplaçant le long d'une ligne droite.
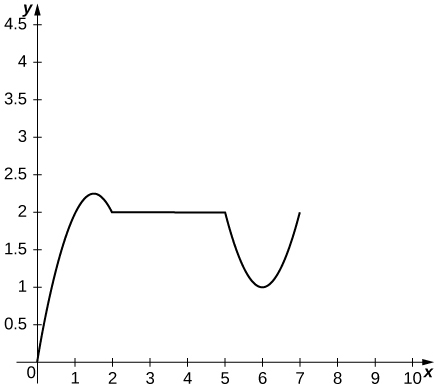
a. Utilisez le graphique de la fonction de position pour déterminer les intervalles de temps pendant lesquels la vitesse est positive, négative ou nulle.
b. Esquissez le graphique de la fonction de vitesse.
c. Utilisez le graphique de la fonction de vitesse pour déterminer les intervalles de temps pendant lesquels l'accélération est positive, négative ou nulle.
d. Déterminez les intervalles de temps pendant lesquels l'objet accélère ou ralentit.
- Réponse
- a. La vélocité est positive en\((0,1.5)∪(6,7)\) marche, négative en\((1.5,2)∪(5,6)\) marche et nulle en marche\((2,5)\).
b.
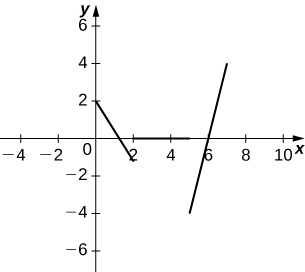
c. L'accélération est positive en\((5,7)\) marche, négative en\((0,2)\) marche et zéro activée\((2,5)\).
d. L'objet accélère\((6,7)∪(1.5,2)\) et ralentit\((0,1.5)∪(5,6)\).
11) La fonction de coût, en dollars, d'une entreprise qui fabrique des robots alimentaires est donnée par\(C(x)=200+\dfrac{7}{x}+\dfrac{x}{27}\), où se\(x\) situe le nombre de robots fabriqués.
a. Déterminez la fonction de coût marginal.
b. Déterminez le coût marginal de fabrication de 12 appareils de transformation des aliments.
c. Déterminez le coût réel de fabrication du treizième robot culinaire.
12) Le prix p (en dollars) et la demande\(x\) pour un certain radio-réveil numérique sont donnés par la fonction prix-demande\(p=10−0.001x\).
a. Trouvez la fonction de recettes\(R(x)\)
b. Déterminez la fonction de revenu marginal.
c. Trouvez le revenu marginal à\(x=2000\) et\(5000\).
- Réponse
- a.\(R(x)=10x−0.001x^2\)
b.\( R′(x)=10−0.002x\)
c. 6$ par article, 0$ par article
13) [T] Un bénéfice est réalisé lorsque les recettes dépassent les coûts. Supposons que la fonction de profit d'un fabricant de planches à roulettes soit donnée par\(P(x)=30x−0.3x^2−250\), où\(x\) est le nombre de planches à roulettes vendues.
a. Trouvez le bénéfice exact de la vente du trentième skateboard.
b. Trouvez la fonction de profit marginal et utilisez-la pour estimer le bénéfice de la vente du trentième skateboard.
14) [T] En général, la fonction de profit est la différence entre les fonctions de recettes et de coûts :\(P(x)=R(x)−C(x)\).
Supposons que les fonctions prix-demande et coût pour la production de perceuses sans fil soient données respectivement par\(p=143−0.03x\) et\(C(x)=75,000+65x\), où\(x\) est le nombre de perceuses sans fil vendues au prix de\(p\) dollars par perceuse et\(C(x)\) le coût de production des perceuses\(x\) sans fil.
a. Déterminez la fonction de coût marginal.
b. Trouvez les fonctions de recettes et de recettes marginales.
c. Trouvez\(R′(1000)\) et\(R′(4000)\). Interprétez les résultats.
d. Déterminez les fonctions de profit et de profit marginal.
e. Trouvez\(P′(1000)\) et\(P′(4000)\). Interprétez les résultats.
- Réponse
- a.\(C′(x)=65\)
b.\(R(x)=143x−0.03x^2\),\(R′(x)=143−0.06x\)
\(R′(1000)=83, \quad R′(4000) = −97\) c. À un niveau de production de 1 000 perceuses sans fil, les recettes augmentent au rythme de 83 dollars par foreuse ; à un niveau de production de 4 000 perceuses sans fil, les recettes diminuent au rythme de 97 dollars par foreuse.
d.\(P(x)=−0.03x^2+78x−75000, \quad P′(x)=−0.06x+78\)
\(P′(1000)=18, \quad P′(4000) =−162\) e. À un niveau de production de 1 000 foreuses sans fil, les bénéfices augmentent au rythme de 18 dollars par foreuse ; à un niveau de production de 4 000 perceuses sans fil, les bénéfices diminuent au rythme de 162 dollars par foreuse.
15) Une petite ville de l'Ohio a chargé un cabinet d'actuaires de mener une étude visant à modéliser le taux de variation de la population de la ville. L'étude a révélé que la population de la ville (mesurée en milliers de personnes) peut être modélisée par la fonction\(P(t)=−\frac{1}{3}t^3+64t+3000\), où elle\(t\) est mesurée en années.
a. Déterminez la fonction du taux de variation\(P′(t)\) de la fonction de population.
b. Trouvez\(P′(1),\; P′(2),\; P′(3)\) et\(P′(4)\). Interprétez ce que les résultats signifient pour la ville.
c. Trouvez\(P''(1),\; P''(2),\; P''(3)\) et\(P''(4)\). Interprétez ce que les résultats signifient pour la population de la ville.
16) [T] Une culture de bactéries croît en nombre en fonction de la fonction\(N(t)=3000(1+\dfrac{4t}{t^2+100})\), où elle\(t\) est mesurée en heures.
a. Déterminez le taux de variation du nombre de bactéries.
b. Trouvez\(N′(0),\; N′(10),\; N′(20)\) et\(N′(30)\).
c. Interpréter les résultats en (b).
d. Trouvez\(N''(0),\; N''(10),\; N''(20),\) et\(N''(30)\). Interprétez ce que les réponses impliquent sur la croissance de la population de bactéries.
- Réponse
- a.\(N′(t)=3000\left(\dfrac{−4t^2+400}{(t^2+100)^2}\right)\)
b.\(120,0,−14.4,−9.6\)
c. La population de bactéries augmente de 0 à 10 heures ; ensuite, elle diminue.
\(0,−6,0.384,0.432\)d. La vitesse à laquelle la bactérie augmente diminue au cours des 10 premières heures. Ensuite, la population de bactéries diminue à un rythme décroissant.
17) La force centripète d'un objet de masse m est donnée par\(F(r)=\dfrac{mv^2}{r}\), où\(v\) est la vitesse de rotation et\(r\) la distance par rapport au centre de rotation.
a. Déterminez le taux de variation de la force centripète par rapport à la distance depuis le centre de rotation.
b. Déterminez le taux de variation de la force centripète d'un objet d'une masse de 1 000 kilogrammes, d'une vitesse de 13,89 m/s et d'une distance du centre de rotation de 200 mètres.
Les questions suivantes concernent la population (en millions) de Londres par décennie au XIXe siècle, qui est répertoriée dans le tableau suivant.
| Année depuis 1800 | Population (millions) |
| 1 | 0,8975 |
| 11 | 1,040 |
| 21 | 1,264 |
| 31 | 1.516 |
| 41 | 1,661 |
| 51 | 2 000 |
| 61 | 2.634 |
| 71 | 3.272 |
| 81 | 3.911 |
| 91 | 4.422 |
Population de LondresSource : http://en.Wikipedia.org/wiki/Demographics_of_London
18) [T]
a. À l'aide d'une calculatrice ou d'un programme informatique, trouvez la fonction linéaire la mieux adaptée pour mesurer la population.
b. Trouvez la dérivée de l'équation dans a. et expliquez sa signification physique.
c. Trouvez la dérivée seconde de l'équation et expliquez sa signification physique.
- Réponse
- a.\(P(t)=0.03983+0.4280\)
\(P′(t)=0.03983\) b. La population augmente.
\(P''(t)=0\)c. Le taux d'augmentation de la population est constant.
19) [T]
a. À l'aide d'une calculatrice ou d'un programme informatique, trouvez la courbe quadratique la mieux adaptée à partir des données.
b. Trouvez la dérivée de l'équation et expliquez sa signification physique.
c. Trouvez la dérivée seconde de l'équation et expliquez sa signification physique.
Pour les exercices suivants, imaginez un astronaute sur une grande planète d'une autre galaxie. Pour en savoir plus sur la composition de cette planète, l'astronaute dépose un capteur électronique dans une tranchée profonde. Le capteur transmet sa position verticale toutes les secondes par rapport à la position de l'astronaute. Le résumé des données du capteur de chute est affiché dans le tableau suivant.
| Temps écoulé après la ou les chutes | Position (m) |
| 0 | 0 |
| 1 | −1 |
| 2 | −2 |
| 3 | −5 |
| 4 | −7 |
| 5 | −14 |
20) [T]
a. À l'aide d'une calculatrice ou d'un programme informatique, trouvez la courbe quadratique la mieux adaptée aux données.
b. Trouvez la dérivée de la fonction de position et expliquez sa signification physique.
c. Trouvez la dérivée seconde de la fonction de position et expliquez sa signification physique.
- Réponse
- a.\(p(t)=−0.6071x^2+0.4357x−0.3571\)
\(p′(t)=−1.214x+0.4357\) b. Il s'agit de la vitesse du capteur.
\(p''(t)=−1.214\)c. Il s'agit de l'accélération du capteur ; il s'agit d'une accélération constante vers le bas.
21) [T]
a. À l'aide d'une calculatrice ou d'un programme informatique, trouvez la courbe cubique la mieux adaptée aux données.
b. Trouvez la dérivée de la fonction de position et expliquez sa signification physique.
c. Trouvez la dérivée seconde de la fonction de position et expliquez sa signification physique.
d. À l'aide du résultat de c., expliquez pourquoi une fonction cubique n'est pas un bon choix pour ce problème.
Les problèmes suivants concernent les équations de type I, II et III de Holling. Ces équations décrivent l'événement écologique de croissance d'une population de prédateurs en fonction de la quantité de proies disponibles pour la consommation.
22) [T] L'équation de Holling de type I est décrite par\(f(x)=ax\), où\(x\) est la quantité de proies disponibles et\(a>0\) la vitesse à laquelle le prédateur rencontre la proie pour la consommation.
a. Représentez graphiquement l'équation de Holling de type I, donnée\(a=0.5\).
b. Déterminez la dérivée première de l'équation de Holling de type I et expliquez physiquement ce que la dérivée implique.
c. Déterminez la dérivée seconde de l'équation de Holling de type I et expliquez physiquement ce que la dérivée implique.
d. À l'aide des interprétations de b. et c., expliquez pourquoi l'équation de Holling de type I peut ne pas être réaliste.
- Réponse
-
un.
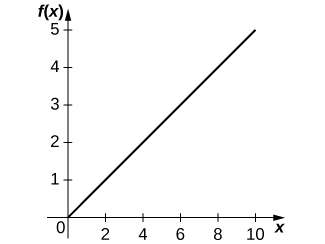
\(f′(x)=a\)b. Plus le nombre de proies augmente, plus les prédateurs se développent.
\(f''(x)=0\)c. À mesure que le nombre de proies augmente, le taux de croissance de la population de prédateurs est constant.
d. Cette équation suppose que s'il y a plus de proies, le prédateur est capable d'augmenter sa consommation de façon linéaire. Cette hypothèse n'est pas physique, car on peut s'attendre à ce qu'il y ait un point de saturation à partir duquel il y a trop de proies pour que le prédateur puisse les consommer correctement.
23) [T] L'équation de Holling de type II est décrite par\(f(x)=\dfrac{ax}{n+x}\), où\(x\) est la quantité de proies disponibles et\(a>0\) le taux de consommation maximal du prédateur.
a. Représenter graphiquement l'équation de Holling de type II donnée\(a=0.5\) et\(n=5\). Quelles sont les différences entre les équations de type I et II de Holling ?
b. Prenez la dérivée première de l'équation de Holling de type II et interprétez la signification physique de la dérivée.
c. Montrez cela\(f(n)=\frac{1}{2}a\) et interprétez la signification du paramètre n.
d. Trouvez et interprétez la signification de la dérivée seconde. Qu'est-ce qui rend la fonction Holling de type II plus réaliste que la fonction Holling de type I ?
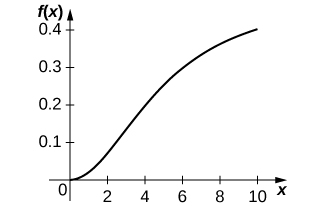
24) [T] L'équation de type III de Holling est décrite par\(f(x)=\dfrac{ax^2}{n^2+x^2}\), où x est la quantité de proies disponibles et\(a>0\) le taux de consommation maximal du prédateur.
a. Représentez graphiquement l'équation de type III de Holling donnée\(a=0.5\) et\(n=5.\) quelles sont les différences entre les équations de type II et III de Holling ?
b. Prenez la dérivée première de l'équation de Holling de type III et interprétez la signification physique de la dérivée.
c. Trouvez et interprétez la signification de la dérivée seconde (il peut être utile de représenter graphiquement la dérivée seconde).
d. Quels phénomènes écologiques supplémentaires la fonction de Holling de type III décrit-elle par rapport à la fonction de Holling de type II ?
- Réponse
-
un.
\(f′(x)=\dfrac{2axn^2}{(n^2+x^2)^2}\)b. Lorsque le nombre de proies augmente, la croissance des prédateurs augmente.
\(f''(x)=\dfrac{2an^2(n^2−3x^2)}{(n^2+x^2)^3}\)c. Lorsque le nombre de proies est extrêmement faible, le taux de croissance des prédateurs augmente, mais lorsque le nombre de proies dépasse un certain seuil, le taux de croissance des prédateurs commence à diminuer.
d. À des niveaux de proies plus faibles, les proies peuvent plus facilement échapper à la détection du prédateur, ce qui réduit le nombre de proies consommées, ce qui réduit la croissance des prédateurs.
25) [T] Les populations de lièvre d'Amérique (en milliers) et de lynx (en centaines) collectées sur une période de 7 ans, de 1937 à 1943, sont présentées dans le tableau suivant. Le lièvre d'Amérique est la principale proie du lynx.
| Population de lièvres d'Amérique (en milliers) | Population de lynx (centaines) |
| 20 | 10 |
| 5 | 15 |
| 65 | 55 |
| 95 | 60 |
Populations de lièvres et de lynx d'Amérique Source : http://www.biotopics.co.uk/newgcse/predatorprey.html.
a. Représentez graphiquement les points de données et déterminez quelle fonction de type Holling convient le mieux aux données.
b. Utiliser la signification des paramètres\(a\) et déterminer\(n\) les valeurs de ces paramètres en examinant un graphique des données. Rappelons que cela\(n\) mesure la valeur des proies qui donne le demi-maximum de la valeur du prédateur.
c. Tracez les fonctions de type Holling I, II et III résultantes au-dessus des données. Le résultat de la partie a. était-il correct ?

