Home
Français
Livre : Calculus (OpenStax)
3 : Produits dérivés
3.4 : Les produits dérivés en tant que taux de variation

3.4 : Les produits dérivés en tant que taux de variation

Last updated
Save as PDF

Page ID: 197809

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Déterminez la nouvelle valeur d'une quantité à partir de l'ancienne valeur et du montant de la variation.
Calculez le taux de variation moyen et expliquez en quoi il diffère du taux de variation instantané.
Appliquez des taux de variation au déplacement, à la vitesse et à l'accélération d'un objet se déplaçant le long d'une ligne droite.
Prédisez la population future à partir de la valeur actuelle et du taux de croissance démographique.
Utilisez des dérivés pour calculer le coût marginal et les recettes dans une situation commerciale.

Dans cette section, nous examinons certaines applications de la dérivée en nous concentrant sur l'interprétation de la dérivée comme étant le taux de variation d'une fonction. Ces applications incluent l'accélération et la vitesse en physique, les taux de croissance démographique en biologie et les fonctions marginales en économie.

Formule du montant de la modification

L'une des applications des dérivées consiste à estimer une valeur inconnue d'une fonction à un point donné en utilisant la valeur connue d'une fonction à un point donné ainsi que son taux de variation à ce point. S'il s'$f(x)$agit d'une fonction définie sur un intervalle$[a,a+h]$, alors la quantité de variation de$f(x)$ sur l'intervalle est la variation des$y$ valeurs de la fonction sur cet intervalle et est donnée par

\[f(a+h)−f(a). \nonumber \]

Le taux moyen de variation de la fonction$f$ sur ce même intervalle est le rapport entre l'ampleur de la variation sur cet intervalle et la variation correspondante$x$ des valeurs. Il est donné par

\[\frac{f(a+h)−f(a)}{h}. \nonumber \]

Comme nous le savons déjà, le taux de variation instantané de$f(x)$ at$a$ est sa dérivée

\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \nonumber \]

Pour des valeurs suffisamment petites de$h$,$f′(a)≈\frac{f(a+h)−f(a)}{h}$. Nous pouvons ensuite résoudre pour$f(a+h)$ obtenir le montant de la formule de changement :

\[f(a+h)≈f(a)+f′(a)h. \label{linapprox} \]

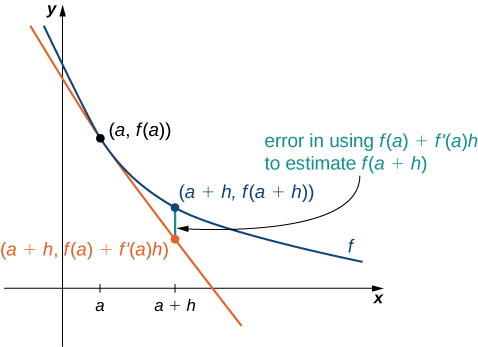
Nous pouvons utiliser cette formule si nous connaissons$f(a)$$f′(a)$ et souhaitons estimer la valeur de$f(a+h)$. Par exemple, nous pouvons utiliser la population actuelle d'une ville et son taux de croissance pour estimer sa population dans un avenir proche. Comme nous pouvons le voir sur la figure$\PageIndex{1}$, nous approximons$f(a+h)$ par la$y$ coordonnée en a+h sur la droite tangente à$f(x)$ at$x=a$. Notez que la précision de cette estimation dépend de$h$ la valeur et de la valeur de$f′(a)$.

Sur le plan de coordonnées cartésien avec a et a+ h marqués sur l'axe x, la fonction f est représentée graphiquement. Il traverse (a, f (a)) et (a + h, f (a + h)). Une ligne droite est tracée à travers (a, f (a)), sa pente étant la dérivée à ce point. Cette droite passe par (a + h, f (a) + f' (a) h). Il existe un segment de droite reliant (a + h, f (a + h)) et (a + h, f (a) + f' (a) h), et il est indiqué qu'il s'agit d'une erreur lors de l'utilisation de f (a) + f' (a) h pour estimer f (a + h). — Figure$\PageIndex{1}$ : La nouvelle valeur d'une quantité modifiée est égale à la valeur initiale plus le taux de variation multiplié par l'intervalle de variation :$f(a+h)≈f(a)+f′(a)h.$

Exemple$\PageIndex{1}$: Estimating the Value of a Function

Si$f(3)=2$ oui$f′(3)=5$, estimez$f(3.2)$.

Solution

Commencez par trouver$h$. Nous avons$h=3.2−3=0.2.$ ainsi,

$f(3.2)=f(3+0.2)≈f(3)+(0.2)f′(3)=2+0.2(5)=3.$

Exercice$\PageIndex{1}$

Donné$f(10)=−5$ et$f′(10)=6$, estimation$f(10.1)$.

Allusion: Utilisez le même processus que dans l'exemple précédent.

Réponse: $−4.4$

Mouvement le long d'une ligne

La dérivée peut également être utilisée pour analyser le mouvement le long d'une ligne. Nous avons décrit la vitesse comme le taux de changement de position. Si nous prenons la dérivée de la vitesse, nous pouvons trouver l'accélération, ou le taux de variation de la vitesse. Il est également important d'introduire l'idée de vitesse, qui est l'amplitude de la vitesse. Ainsi, nous pouvons énoncer les définitions mathématiques suivantes.

Définition

$s(t)$Soit une fonction donnant la position d'un objet à l'instant t.

La vitesse de l'objet dans le temps$t$ est donnée par$v(t)=s′(t)$.
La vitesse de l'objet à la fois$t$ est donnée par$|v(t)|$.
L'accélération de l'objet at$t$ est donnée par$a(t)=v′(t)=s''(t)$.

Exemple$\PageIndex{2}$: Comparing Instantaneous Velocity and Average Velocity

Une balle est lâchée d'une hauteur de 64 pieds. Sa hauteur au-dessus du sol (en pieds)$t$ quelques secondes plus tard est donnée par$s(t)=−16t^2+64$.

$Sur le plan de coordonnées cartésien, la fonction s (t) = −16t2 + 64 est représentée graphiquement. Cette fonction commence à (0, 64) et diminue jusqu'à (0, 2).$

Quelle est la vitesse instantanée de la balle lorsqu'elle touche le sol ?
Quelle est la vitesse moyenne lors de sa chute ?

Solution

La première chose à faire est de déterminer le temps qu'il faut à la balle pour atteindre le sol. Pour ce faire, réglez$s(t)=0$. $−16t^2+64=0$En résolvant, on obtient$t=2$, il faut donc 2 secondes pour que la balle atteigne le sol.

La vitesse instantanée de la balle lorsqu'elle touche le sol est de$v(2)$. Depuis$v(t)=s′(t)=−32t$, nous obtenons$v(t)=−64$ ft/s.
La vitesse moyenne de la balle lors de sa chute est

$v_{ave}=\frac{s(2)−s(0)}{2−0}=\frac{0−64}{2}=−32$pieds/s.

Exemple$\PageIndex{3}$: Interpreting the Relationship between $v(t)$ and $a(t)$

Une particule se déplace le long d'un axe de coordonnées dans la direction positive vers la droite. Sa position dans le temps$t$ est donnée par$s(t)=t^3−4t+2$. Trouvez$v(1)$$a(1)$ et utilisez ces valeurs pour répondre aux questions suivantes.

La particule se déplace-t-elle de gauche à droite ou de droite à gauche à la fois$t=1$ ?
La particule augmente-t-elle ou ralentit-elle de temps en temps$t=1$ ?

Solution

Commencez par trouver$v(t)$ et$a(t)$.

$v(t) = s'(t) = 3t^2 - 4$et$a(t)=v′(t)=s''(t)=6t$.

En évaluant ces fonctions à$t=1$, nous obtenons$v(1)=−1$ et$a(1)=6$.

Parce$v(1)<0$ que la particule se déplace de droite à gauche.
Parce que$v(1)<0$ et$a(1)>0$, la vitesse et l'accélération agissent dans des directions opposées. En d'autres termes, la particule est accélérée dans la direction opposée à la direction dans laquelle elle se déplace, ce qui$|v(t)|$ entraîne sa diminution. La particule ralentit.

Exemple$\PageIndex{4}$: Position and Velocity

La position d'une particule se déplaçant le long d'un axe de coordonnées est donnée par$s(t)=t^3−9t^2+24t+4,\; t≥0.$

Trouvez$v(t)$.
À quelle (s) heure (s) la particule est-elle au repos ?
À quels intervalles de temps la particule se déplace-t-elle de gauche à droite ? De droite à gauche ?
Utilisez les informations obtenues pour esquisser la trajectoire de la particule le long d'un axe de coordonnées.

Solution

a. La vitesse est la dérivée de la fonction de position :

$v(t)=s′(t)=3t^2−18t+24.$

b. La particule est au repos lorsque$v(t)=0$, ainsi réglée$3t^2−18t+24=0$. La factorisation du côté gauche de l'équation produit$3(t−2)(t−4)=0$. En résolvant, nous trouvons que la particule est au repos à$t=2$ et$t=4$.

c. La particule se déplace de gauche à droite quand$v(t)>0$ et de droite à gauche quand$v(t)<0$. La figure$\PageIndex{2}$ donne l'analyse du signe de$v(t)$ pour$t≥0$, mais elle ne représente pas l'axe le long duquel se déplace la particule.

Une ligne numérique marquée par 0, 2 et 4. Entre 0 et 2, il y a un signe plus. Au-dessus de 2, il y a un 0. Entre 2 et 4, il y a un signe négatif. Au-dessus de 4, il y a un 0. Après 4, il y a un signe plus et v (t). — Figure : Le$\PageIndex{2}$ signe de détermine$v(t)$ la direction de la particule.

Depuis$[0,2)∪(4,+∞)$,$3t^2−18t+24>0$ la particule se déplace de gauche à droite sur ces intervalles.
Depuis$(2,4)$,$3t^2−18t+24<0$ la particule se déplace de droite à gauche sur cet intervalle.

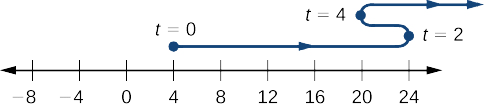
d. Avant de pouvoir dessiner le graphe de la particule, nous devons connaître sa position au moment où elle commence à se déplacer$(t=0)$ et au moment où elle change de direction$(t=2,4)$. Nous avons$s(0)=4$$s(2)=24$, et$s(4)=20$. Cela signifie que la particule commence sur l'axe des coordonnées$4$ et change de direction sur$24$ et$20$ sur l'axe des coordonnées. La trajectoire de la particule est indiquée sur un axe de coordonnées sur la figure$\PageIndex{3}$.

Une ligne numérique est donnée et au-dessus, une ligne serpente, en commençant par t = 0 au-dessus de 4 sur la ligne numérique. La ligne à t = 2 est alors supérieure à 24 sur la ligne numérique. Ensuite, la droite diminue à t = 4 pour se situer au-dessus de 20 sur la droite numérique, après quoi elle change de direction à nouveau et augmente indéfiniment. — Figure$\PageIndex{3}$ : Le trajet de la particule peut être déterminé par analyse$v(t)$.

Exercice$\PageIndex{2}$

Une particule se déplace le long d'un axe de coordonnées. Sa position dans le temps$t$ est donnée par$s(t)=t^2−5t+1$. La particule se déplace-t-elle de droite à gauche ou de gauche à droite à la fois$t=3$ ?

Allusion: Trouvez$v(3)$ et regardez le panneau.

Réponse: de gauche à droite

Évolution démographique

En plus d'analyser la vitesse, la vitesse, l'accélération et la position, nous pouvons utiliser des dérivés pour analyser divers types de populations, y compris des populations aussi diverses que les colonies de bactéries et les villes. Nous pouvons utiliser une population actuelle, associée à un taux de croissance, pour estimer la taille d'une population future. Le taux de croissance démographique est le taux de variation d'une population et peut donc être représenté par la dérivée de la taille de la population.

Définition

Si$P(t)$ est le nombre d'entités présentes dans une population, alors le taux de croissance démographique de$P(t)$ est défini comme étant égal à$P′(t)$.

Exemple$\PageIndex{5}$: Estimating a Population

La population d'une ville triple tous les 5 ans. Si sa population actuelle est de 10 000 habitants, quelle sera sa population approximative dans deux ans ?

Solution

$P(t)$Soyons la population (en milliers) dans des$t$ années. Ainsi, nous le savons$P(0)=10$ et, sur la base des informations, nous anticipons$P(5)=30$. Estimez maintenant$P′(0)$ le taux de croissance actuel, en utilisant

$P′(0)≈\frac{P(5)−P(0)}{5−0}=\frac{30−10}{5}=4$.

En appliquant l'équation \ ref {linapprox} à$P(t)$, nous pouvons estimer la population dans 2 ans en écrivant

$P(2)≈P(0)+(2)P′(0)≈10+2(4)=18$;

ainsi, dans deux ans, la population sera de 18 000 habitants.

Exercice$\PageIndex{3}$

La population actuelle d'une colonie de moustiques est connue pour être de 3 000, c'est-à-dire$P(0)=3,000$. Si$P′(0)=100$, estimez la taille de la population en 3 jours, où$t$ est mesurée en jours.

Allusion: Utiliser$P(3)≈P(0)+3P′(0)$

Réponse: 3 300

Évolution des coûts et des recettes

Outre l'analyse du mouvement le long d'une ligne et de la croissance démographique, les dérivés sont utiles pour analyser les variations des coûts, des revenus et des bénéfices. Le concept de fonction marginale est courant dans les domaines des affaires et de l'économie et implique l'utilisation de produits dérivés. Le coût marginal est la dérivée de la fonction de coût. Le revenu marginal est le dérivé de la fonction de recettes. Le bénéfice marginal est la dérivée de la fonction de profit, qui est basée sur la fonction de coût et la fonction de recettes.

Définition

Si$C(x)$ c'est le coût de production des$x$ articles, alors le coût marginal l'$MC(x)$est$MC(x)=C′(x)$.
Si$R(x)$ c'est le revenu obtenu grâce à la vente d'$x$articles, alors le revenu marginal l'$MR(x)$est$MR(x)=R′(x)$.
S'il s'$P(x)=R(x)−C(x)$agit du bénéfice obtenu grâce à la vente d'$x$articles, alors le bénéfice marginal$MP(x)$ est défini comme étant$MP(x)=P′(x)=MR(x)−MC(x)=R′(x)−C′(x)$.

Nous pouvons approximativement

\[MC(x)=C′(x)=\lim_{h→0}\frac{C(x+h)−C(x)}{h} \nonumber \]

en choisissant une valeur appropriée pour$h$. Puisque$x$ représente des objets, une valeur faible et raisonnable pour$h$ est 1. Ainsi, en substituant$h=1$, nous obtenons l'approximation$MC(x)=C′(x)≈C(x+1)−C(x)$. Par conséquent,$C′(x)$ pour une valeur donnée de,$x$ peut être considérée comme la variation du coût associée à la production d'un article supplémentaire. De la même manière,$MR(x)=R′(x)$ se rapproche du revenu obtenu par la vente d'un article supplémentaire et$MP(x)=P′(x)$ du bénéfice obtenu par la production et la vente d'un article supplémentaire.

Exemple$\PageIndex{6}$: Applying Marginal Revenue

Supposons que le nombre de dîners barbecue pouvant être vendus peut être lié au prix facturé$p$, par l'équation$p(x)=9−0.03x,0≤x≤300$.$x$

Dans ce cas, les recettes en dollars obtenues par la vente de dîners au$x$ barbecue sont données par

$R(x)=xp(x)=x(9−0.03x)=−0.03x^2+9x\;\text{ for }0≤x≤300$.

Utilisez la fonction de revenu marginal pour estimer les recettes provenant de la vente du dîner$101^{\text{st}}$ barbecue. Comparez cela aux recettes réelles provenant de la vente de ce dîner.

Solution

Déterminez d'abord la fonction de revenu marginal :$MR(x)=R′(x)=−0.06x+9.$

Ensuite, utilisez$R′(100)$ à titre approximatif$R(101)−R(100)$ les recettes provenant de la vente du$101^{\text{st}}$ dîner. Depuis$R′(100)=3$, les recettes provenant de la vente du$101^{\text{st}}$ dîner sont d'environ 3$.

Les recettes réelles provenant de la vente du$101^{\text{st}}$ dîner sont

$R(101)−R(100)=602.97−600=2.97,$ou$$2.97.$

Le revenu marginal est une assez bonne estimation dans ce cas et présente l'avantage d'être facile à calculer.

Exercice$\PageIndex{4}$

Supposons que le bénéfice tiré de la vente de dîners$x$ à base de poisson soit donné par$P(x)=−0.03x^2+8x−50$. Utilisez la fonction de profit marginal pour estimer le bénéfice de la vente du dîner$101^{\text{st}}$ frit.

Allusion: $P′(100)$À utiliser pour approximer$P(101)−P(100)$.

Réponse: 2$

Concepts clés

En utilisant$f(a+h)≈f(a)+f′(a)h$, il est possible d'estimer$f(a+h)$ un$f′(a)$ et$f(a)$.
Le taux de changement de position est la vitesse, et le taux de changement de vitesse est l'accélération. La vitesse est la valeur absolue, ou amplitude, de la vitesse.
Le taux de croissance démographique et la population actuelle peuvent être utilisés pour prédire la taille d'une population future.
Les fonctions de coût marginal, de revenu marginal et de profit marginal peuvent être utilisées pour prédire, respectivement, le coût de production d'un article supplémentaire, le revenu obtenu par la vente d'un article supplémentaire et le bénéfice obtenu par la production et la vente d'un article supplémentaire.

Lexique

accélération: est le taux de variation de la vitesse, c'est-à-dire la dérivée de la vitesse

montant de la monnaie: la quantité d'une fonction$f(x)$ sur un intervalle$[x,x+h] is f(x+h)−f(x)$

taux de variation moyen: est une fonction$f(x)$ sur un intervalle$[x,x+h]$ est$\frac{f(x+h)−f(a)}{b−a}$

coût marginal: est la dérivée de la fonction de coût, ou le coût approximatif de production d'un article supplémentaire

recettes marginales: est la dérivée de la fonction de chiffre d'affaires, ou le chiffre d'affaires approximatif obtenu en vendant un article supplémentaire

bénéfice marginal: est la dérivée de la fonction de profit, ou le bénéfice approximatif obtenu en produisant et en vendant un article supplémentaire

taux de croissance démographique: est la dérivée de la population par rapport au temps

vitesse: est la valeur absolue de la vitesse, c'$|v(t)|$est-à-dire la vitesse d'un objet au temps$t$ dont la vitesse est donnée par$v(t)$

Exemple\(\PageIndex{1}\): Estimating the Value of a Function

Exercice\(\PageIndex{1}\)

Définition

Exemple\(\PageIndex{2}\): Comparing Instantaneous Velocity and Average Velocity

Exemple\(\PageIndex{3}\): Interpreting the Relationship between \(v(t)\) and \(a(t)\)

Exemple\(\PageIndex{4}\): Position and Velocity

Exercice\(\PageIndex{2}\)

Définition

Exemple\(\PageIndex{5}\): Estimating a Population

Exercice\(\PageIndex{3}\)

Définition

Exemple\(\PageIndex{6}\): Applying Marginal Revenue

Exercice\(\PageIndex{4}\)