3.5E : Exercices pour la section 3.5

Last updated
Save as PDF

Page ID: 197781

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 10,$\dfrac{dy}{dx}$ recherchez les fonctions données.

1)$y=x^2−\sec x+1$

Réponse: $\dfrac{dy}{dx}=2x−\sec x\tan x$

2)$y=3\csc x+\dfrac{5}{x}$

3)$y=x^2\cot x$

Réponse: $\dfrac{dy}{dx}=2x\cot x−x^2\csc^2 x$

4)$y=x−x^3\sin x$

5)$y=\dfrac{\sec x}{x}$

Réponse: $\dfrac{dy}{dx}=\dfrac{x\sec x\tan x−\sec x}{x^2}$

6)$y=\sin x\tan x$

7)$y=(x+\cos x)(1−\sin x)$

Réponse: $\dfrac{dy}{dx}=(1−\sin x)(1−\sin x)−\cos x(x+\cos x)$

8)$y=\dfrac{\tan x}{1−\sec x}$

9)$y=\dfrac{1−\cot x}{1+\cot x}$

Réponse: $\dfrac{dy}{dx}=\dfrac{2\csc^2 x}{(1+\cot x)^2}$

10)$y=(\cos x)(1+\csc x)$

Dans les exercices 11 à 16, trouvez l'équation de la tangente à chacune des fonctions données aux valeurs indiquées de$x$. Utilisez ensuite un calculateur pour représenter graphiquement la fonction et la droite tangente afin de vous assurer que l'équation de la tangente est correcte.

11) [T]$f(x)=−\sin x,\quad x=0$

Réponse

$y=−x$

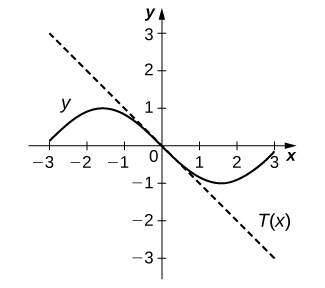
$Le graphique montre un sin négatif (x) et la droite T (x) avec une pente -1 et une intersection y 0.$

12) [T]$f(x)=\csc x,\quad x=\frac{π}{2}$

13) [T]$f(x)=1+\cos x,\quad x=\frac{3π}{2}$

Réponse

$y=x+\frac{2−3π}{2}$

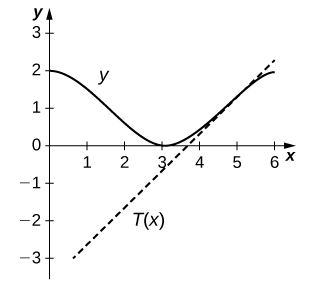
$Le graphique montre la fonction cosinus décalée d'un point vers le haut et possède la droite T (x) avec la pente 1 et l'intersection y (2 — 3π) /2.$

14) [T]$f(x)=\sec x,\quad x=\frac{π}{4}$

15) [T]$f(x)=x^2−\tan x, \quad x=0$

Réponse

$y=−x$

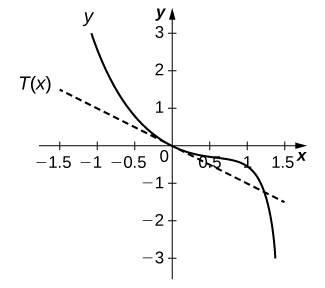
$Le graphique montre que la fonction commence à (−1, 3), diminue jusqu'à l'origine, continue de diminuer lentement jusqu'à environ (1, −0,5), point auquel elle diminue très rapidement.$

16) [T]$f(x)=5\cot x, \quad x=\frac{π}{4}$

Dans les exercices 17 à 22,$\dfrac{d^2y}{dx^2}$ recherchez les fonctions données.

17)$y=x\sin x−\cos x$

Réponse: $\dfrac{d^2y}{dx^2} = 3\cos x−x\sin x$

18)$y=\sin x\cos x$

19)$y=x−\frac{1}{2}\sin x$

Réponse: $\dfrac{d^2y}{dx^2} = \frac{1}{2}\sin x$

(20)$y=\dfrac{1}{x}+\tan x$

(21)$y=2\csc x$

Réponse: $\dfrac{d^2y}{dx^2} = 2\csc(x)\left(\csc^2(x)+\cot^2(x)\right) $

22)$y=\sec^2 x$

23) Trouvez toutes les$x$ valeurs sur le graphique$f(x)=−3\sin x\cos x$ indiquant où la tangente est horizontale.

Réponse: $x = \dfrac{(2n+1)π}{4}$, où$n$ est un entier

24) Trouvez toutes les$x$ valeurs sur le graphique$f(x)=x−2\cos x$ pour$0<x<2π$ lesquelles la tangente a une pente 2.

25)$f(x)=\cot x.$ Déterminons les points sur$f$ le graphique$0<x<2π$ où la ou les lignes tangentes sont parallèles à la droite$y=−2x$.

Réponse: $\left(\frac{π}{4},1\right),\quad \left(\frac{3π}{4},−1\right),\quad\left(\frac{5π}{4},1\right),\quad \left(\frac{7π}{4},−1\right)$

26) [T] Une masse sur un ressort rebondit de haut en bas selon un mouvement harmonique simple, modélisé par la fonction$s(t)=−6\cos t$ où s est mesuré en pouces et$t$ est mesuré en secondes. Détermine la vitesse à laquelle le ressort oscille en$t=5$ s.

27) Laissez la position d'un pendule oscillant dans un mouvement harmonique simple être donnée par$s(t)=a\cos t+b\sin t$. Trouvez les constantes$a$ et$b$ telles que lorsque la vitesse est de 3 cm/s,$s=0$ et$t=0$.

Réponse: $a=0,\quad b=3$

28) Une fois qu'un plongeur saute d'un plongeoir, le bord du plongeon oscille avec la position donnée en$s(t)=−5\cos t$ cm$t$ quelques secondes après le saut.

a. Esquissez une période de la fonction de position pour$t≥0$.

b. Trouvez la fonction de vitesse.

c. Esquissez une période de la fonction de vitesse pour$t≥0$.

d. Déterminez les moments où la vitesse est$0$ supérieure à une période.

e. Trouvez la fonction d'accélération.

f. Esquissez une période de la fonction d'accélération pour$t≥0$.

29) Le nombre de hamburgers vendus dans un restaurant de restauration rapide de Pasadena, en Californie, est indiqué$y=10+5\sin x$ par$y$ le nombre de hamburgers vendus et$x$ représente le nombre d'heures suivant l'ouverture du restaurant, de 11 h à 23 h, date de fermeture du magasin. Trouvez$y'$ et déterminez les intervalles où le nombre de hamburgers vendus augmente.

Réponse: $y′=5\cos(x)$, en hausse par rapport à$\left(0,\frac{π}{2}\right),\;\left(\frac{3π}{2},\frac{5π}{2}\right)$, et$\left(\frac{7π}{2},12\right)$

30) [T] La quantité de pluie par mois à Phoenix, en Arizona, peut être approximée par$y(t)=0.5+0.3\cos t$, où$t$ se situent les mois depuis janvier. Trouvez$y′$ et utilisez une calculatrice pour déterminer les intervalles où la quantité de pluie qui tombe diminue.

Pour les exercices 31 à 33, utilisez la règle du quotient pour dériver les équations données.

31)$\dfrac{d}{dx}(\cot x)=−\csc^2x$

32)$\dfrac{d}{dx}(\sec x)=\sec x\tan x$

33)$\dfrac{d}{dx}(\csc x)=−\csc x\cot x$

34) Utilisez la définition du dérivé et de l'identité$\cos(x+h)=\cos x\cos h−\sin x\sin h$ pour le prouver$\dfrac{d}{dx}(\cos x)=−\sin x$.

Pour les exercices 35 à 39, trouvez la dérivée d'ordre supérieur demandée pour les fonctions données.

35)$\dfrac{d^3y}{dx^3}$ de$y=3\cos x$

Réponse: $\dfrac{d^3y}{dx^3} = 3\sin x$

36)$\dfrac{d^2y}{dx^2}$ de$y=3\sin x+x^2\cos x$

37)$\dfrac{d^4y}{dx^4}$ de$y=5\cos x$

Réponse: $\dfrac{d^4y}{dx^4} = 5\cos x$

38)$\dfrac{d^2y}{dx^2}$ de$y=\sec x+\cot x$

39)$\dfrac{d^3y}{dx^3}$ de$y=x^{10}−\sec x$

Réponse: $\dfrac{d^3y}{dx^3} = 720x^7−5\tan(x)\sec^3(x)−\tan^3(x)\sec(x)$