3.3 : Règles de différenciation
- Page ID
- 197841
- Indiquez la constante, le multiple constant et les règles de puissance.
- Appliquez les règles de somme et de différence pour combiner des dérivés.
- Utilisez la règle du produit pour trouver la dérivée d'un produit de fonctions.
- Utilisez la règle du quotient pour déterminer la dérivée d'un quotient de fonctions.
- Étendez la règle de puissance aux fonctions avec des exposants négatifs.
- Combinez les règles de différenciation pour trouver la dérivée d'une fonction polynomiale ou rationnelle.
Trouver des dérivées de fonctions à l'aide de la définition de la dérivée peut être un processus long et, pour certaines fonctions, assez difficile. Par exemple, nous avons précédemment constaté que
\[\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}} \nonumber \]
en utilisant un procédé qui impliquait de multiplier une expression par un conjugué avant d'évaluer une limite.
Le processus que nous pourrions utiliser pour évaluer à\(\dfrac{d}{dx}\left(\sqrt[3]{x}\right)\) l'aide de la définition, bien que similaire, est plus complexe.
Dans cette section, nous développons des règles pour trouver des dérivés qui nous permettent de contourner ce processus. Nous commençons par les bases.
Les règles de base
Les fonctions\(f(x)=c\) et\(g(x)=x^n\) où\(n\) est un entier positif sont les éléments de base à partir desquels tous les polynômes et les fonctions rationnelles sont construits. Pour trouver efficacement les dérivées des polynômes et des fonctions rationnelles sans recourir à la définition limite de la dérivée, nous devons d'abord développer des formules permettant de différencier ces fonctions de base.
La règle constante
Nous appliquons d'abord la définition limite de la dérivée pour trouver la dérivée de la fonction constante,\(f(x)=c\). Pour cette fonction, à la fois\(f(x)=c\) et\(f(x+h)=c\), nous obtenons donc le résultat suivant :
\[\begin{align*} f′(x) &=\lim_{h→0} \dfrac{f(x+h)−f(x)}{h} \\[4pt] &=\lim_{h→0}\dfrac{c−c}{h} \\[4pt] &=\lim_{h→0}\dfrac{0}{h} \\[4pt] &=\lim_{h→0}0=0. \end{align*}\]
La règle de différenciation des fonctions constantes est appelée règle des constantes. Il indique que la dérivée d'une fonction constante est nulle ; c'est-à-dire qu'une fonction constante est une ligne horizontale, la pente, ou le taux de variation, d'une fonction constante l'est\(0\). Nous reformulons cette règle dans le théorème suivant.
\(c\)Soyons une constante. Si\(f(x)=c\), alors\(f′(x)=0.\)
Nous pouvons également exprimer cette règle comme suit :
\[\dfrac{d}{dx}(c)=0. \nonumber \]
Trouvez le dérivé de\(f(x)=8.\)
Solution
Il s'agit simplement d'une application de la règle en une étape :\(f′(8)=0.\)
Trouvez le dérivé de\(g(x)=−3\).
- Allusion
-
Utilisez l'exemple précédent comme guide
- Réponse
-
0
La règle du pouvoir
Nous avons démontré que
\[\dfrac{d}{dx}\left(x^2\right)=2x\quad\text{ and }\quad\dfrac{d}{dx}\left(x^{1/2}\right)=\dfrac{1}{2}x^{−1/2}. \nonumber \]
À ce stade, vous pouvez voir un schéma commencer à se développer pour les dérivés du formulaire\(\dfrac{d}{dx}\left(x^n\right)\). Nous poursuivons notre examen des formules dérivées en différenciant les fonctions de puissance sous la forme\(f(x)=x^n\) où\(n\) est un entier positif. Nous développons des formules pour les dérivées de ce type de fonction par étapes, en commençant par des puissances entières positives. Avant d'énoncer et de prouver la règle générale pour les dérivées de fonctions de cette forme, nous examinons un cas spécifique\(\dfrac{d}{dx}(x^3)\). Au cours de cette dérivation, portez une attention particulière à la partie de l'expression en gras, car la technique utilisée dans ce cas est essentiellement la même que celle utilisée pour prouver le cas général.
Trouvez\(\dfrac{d}{dx}\left(x^3\right)\).
Solution :
| \(\displaystyle \dfrac{d}{dx}\left(x^3\right)=\lim_{h→0}\dfrac{(x+h)^3−x^3}{h}\) | |
| \(\displaystyle =\lim_{h→0}\dfrac{x^3+3x^2h+3xh^2+h^3−x^3}{h}\) | Notez que le premier terme de l'expansion de\((x+h)^3\) est\(x^3\) et que le second terme est\(3x^2h\). Tous les autres termes contiennent des pouvoirs\(h\) égaux ou supérieurs à deux |
| \(\displaystyle =\lim_{h→0}\dfrac{3x^2h+3xh^2+h^3}{h}\) | À cette étape, les\(x^3\) termes ont été annulés, ne laissant que les termes contenant\(h\). |
| \(\displaystyle =\lim_{h→0}\dfrac{h(3x^2+3xh+h^2)}{h}\) | Éliminez le facteur commun de\(h\). |
| \(\displaystyle =\lim_{h→0}(3x^2+3xh+h^2)\) | Après avoir annulé le facteur commun de\(h\), le seul terme qui ne contient pas\(h\) est\(3x^2\). |
| \(=3x^2\) | \(h\)Lâchez\(0\). |
Trouvez\(\dfrac{d}{dx}\left(x^4\right).\)
- Allusion
-
Utilisez\((x+h)^4=x^4+4x^3h+6x^2h^2+4xh^3+h^4\) et suivez la procédure décrite dans l'exemple précédent.
- Réponse
-
\(\dfrac{d}{dx}\left(x^4\right) = 4x^3\)
Comme nous le verrons, la procédure pour trouver la dérivée de la forme générale\(f(x)=x^n\) est très similaire. Bien qu'il soit souvent imprudent de tirer des conclusions générales à partir d'exemples spécifiques, nous remarquons que lorsque nous différencions\(f(x)=x^3\), la puissance sur\(x\) devient le coefficient de\(x^2\) dans la dérivée et la puissance sur\(x\) la dérivée diminue de 1. Le théorème suivant indique que la règle de puissance s'applique à toutes les puissances entières positives de\(x\). Nous allons éventuellement étendre ce résultat aux puissances entières négatives. Plus tard, nous verrons que cette règle peut également être étendue d'abord aux pouvoirs rationnels de,\(x\) puis aux pouvoirs arbitraires de\(x\). Sachez toutefois que cette règle ne s'applique pas aux fonctions dans lesquelles une constante est élevée à une puissance variable, telle que\(f(x)=3^x\).
\(n\)Soit un entier positif. Si\(f(x)=x^n\), alors
\[f′(x)=nx^{n−1}. \nonumber \]
Nous pouvons également exprimer cette règle comme suit :
\[\dfrac{d}{dx}\left(x^n\right)=nx^{n−1.} \nonumber \]
Pour\(f(x)=x^n\) où\(n\) est un entier positif, nous avons
\[f′(x)=\lim_{h→0}\dfrac{(x+h)^n−x^n}{h}. \nonumber \]
Depuis
\((x+h)^n=x^n+nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n,\)
nous voyons que
\((x+h)^n−x^n=nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n.\)
Ensuite, divisez les deux côtés par h :
\(\dfrac{(x+h)^n−x^n}{h}=\dfrac{nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n}{h}.\)
Ainsi,
\(\dfrac{(x+h)^n−x^n}{h}=nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n−1}.\)
Enfin,
\[f′(x)=\lim_{h→0}(nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n-1}) \nonumber \]
\(=nx^{n−1}.\)
□
Trouvez la dérivée de la fonction\(f(x)=x^{10}\) en appliquant la règle de puissance.
Solution
En utilisant la règle du pouvoir avec\(n=10\), nous obtenons
\[f'(x)=10x^{10−1}=10x^9. \nonumber \]
Trouvez le dérivé de\(f(x)=x^7\).
- Allusion
-
Utilisez la règle de puissance avec\(n=7.\)
- Réponse
-
\(f′(x)=7x^6\)
La somme, la différence et les règles multiples constantes
Nous trouvons nos prochaines règles de différenciation en examinant les dérivées des sommes, des différences et des multiples constants de fonctions. Tout comme lorsque nous travaillons avec des fonctions, certaines règles permettent de trouver plus facilement les dérivées de fonctions que nous ajoutons, soustrayons ou multiplions par une constante. Ces règles sont résumées dans le théorème suivant.
Laissez\(f(x)\) et\(g(x)\) soyez des fonctions différenciables et\(k\) soyez une constante. Chacune des équations suivantes est alors valable.
Règle de somme. La dérivée de la somme d'une fonction\(f\) et d'une fonction\(g\) est identique à la somme de la dérivée de\(f\) et de la dérivée de\(g\).
\[\dfrac{d}{dx}\big(f(x)+g(x)\big)=\dfrac{d}{dx}\big(f(x)\big)+\dfrac{d}{dx}\big(g(x)\big); \nonumber \]
c'est-à-dire
\[\text{for }s(x)=f(x)+g(x),\quad s′(x)=f′(x)+g′(x). \nonumber \]
Règle de différence. La dérivée de la différence entre une fonction\(f\) et une fonction\(g\) est identique à la différence entre la dérivée de\(f\) et la dérivée de\(g\) :
\[\dfrac{d}{dx}(f(x)−g(x))=\dfrac{d}{dx}(f(x))−\dfrac{d}{dx}(g(x)); \nonumber \]
c'est-à-dire
\[\text{for }d(x)=f(x)−g(x),\quad d′(x)=f′(x)−g′(x). \nonumber \]
Règle multiple constante. La dérivée d'une constante\(k\) multipliée par une fonction\(f\) est identique à la constante multipliée par la dérivée :
\[\dfrac{d}{dx}\big(kf(x)\big)=k\dfrac{d}{dx}\big(f(x)\big); \nonumber \]
c'est-à-dire
\[\text{for }m(x)=kf(x),\quad m′(x)=kf′(x). \nonumber \]
Nous ne fournissons ici que la preuve de la règle de la somme. Les autres suivent de la même manière.
Pour des fonctions différenciables\(f(x)\) et\(g(x)\), nous définissons\(s(x)=f(x)+g(x)\). En utilisant la définition limite de la dérivée que nous avons
\[s′(x)=\lim_{h→0}\dfrac{s(x+h)−s(x)}{h}.\nonumber \]
En substituant\(s(x+h)=f(x+h)+g(x+h)\) et\(s(x)=f(x)+g(x),\) nous obtenons
\[s′(x)=\lim_{h→0}\dfrac{\big(f(x+h)+g(x+h)\big)−\big(f(x)+g(x)\big)}{h}.\nonumber \]
En réorganisant et en regroupant les termes, nous avons
\[s′(x)=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}+\dfrac{g(x+h)−g(x)}{h}\right).\nonumber \]
Nous appliquons maintenant la loi de la somme pour les limites et la définition de la dérivée pour obtenir
\[s′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}+\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}=f′(x)+g′(x).\nonumber \]
□
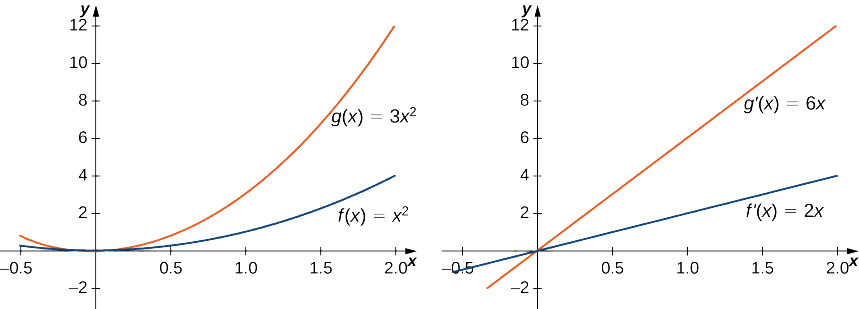
Trouvez la dérivée de\(g(x)=3x^2\) et comparez-la à la dérivée de\(f(x)=x^2.\)
Solution
Nous utilisons directement la règle du pouvoir :
\[g′(x)=\dfrac{d}{dx}(3x^2)=3\dfrac{d}{dx}(x^2)=3(2x)=6x.\nonumber \]
Puisque\(f(x)=x^2\) possède une dérivée\(f′(x)=2x\), nous voyons que la dérivée de\(g(x)\) est 3 fois la dérivée de\(f(x)\). Cette relation est illustrée dans la figure\(\PageIndex{1}\).
Trouvez le dérivé de\(f(x)=2x^5+7\).
Solution
Nous commençons par appliquer la règle de différenciation de la somme de deux fonctions, suivie des règles de différenciation des multiples constants de fonctions et de la règle de différenciation des pouvoirs. Pour mieux comprendre l'ordre dans lequel les règles de différenciation sont appliquées, nous utilisons la notation Leibniz tout au long de la solution :
\ (\ begin {align*} f′ (x) &= \ dfrac {d} {dx} \ left (2x^5+7 \ right) \ \ [4pt]
&= \ dfrac {d} {dx} (2x^5) + \ dfrac {d} {dx} (7) & & \ text {Appliquez la règle de la somme.} \ \ [4pt]
&=2 \ dfrac {d} {dx} (x^5) + \ dfrac {d} {dx} (7) & \ text {Appliquez la règle des multiples constants.} \ \ [4pt]
&=2 (5) x^4) +0 & & \ text {Appliquez la règle de puissance et la règle des constantes.} \ \ [4 points]
&=10x^4 & & \ text {Simplifier.} \ end {align*} \)
Trouvez le dérivé de\(f(x)=2x^3−6x^2+3.\)
- Allusion
-
Utilisez l'exemple précédent comme guide.
- Réponse
-
\(f′(x)=6x^2−12x.\)
Trouve l'équation de la droite tangente au graphe de\(f(x)=x^2−4x+6\) at\(x=1\)
Solution
Pour trouver l'équation de la tangente, il faut un point et une pente. Pour trouver le point, calculez
\[f(1)=1^2−4(1)+6=3. \nonumber \]
Cela nous donne raison\((1,3)\). Puisque la pente de la tangente à 1 est\(f′(1)\), il faut d'abord trouver\(f′(x)\). En utilisant la définition d'un dérivé, nous avons
\[f′(x)=2x−4\nonumber \]
donc la pente de la tangente est\(f′(1)=−2\). En utilisant la formule de pente ponctuelle, nous voyons que l'équation de la droite tangente est
\[y−3=−2(x−1).\nonumber \]
En mettant l'équation de la droite sous forme d'intersection de pente, nous obtenons
\[y=−2x+5.\nonumber \]
Détermine l'équation de la droite tangente au graphe de\(f(x)=3x^2−11\) at\(x=2\). Utilisez la forme à pente ponctuelle.
- Allusion
-
Utilisez l'exemple précédent comme guide.
- Réponse
-
\(y=12x−23\)
La règle du produit
Maintenant que nous avons examiné les règles de base, nous pouvons commencer à examiner certaines des règles les plus avancées. Le premier examine la dérivée du produit de deux fonctions. Bien qu'il puisse être tentant de supposer que le dérivé du produit est le produit des dérivés, comme c'est le cas pour les règles de somme et de différence, la règle du produit ne suit pas ce schéma. Pour comprendre pourquoi nous ne pouvons pas utiliser ce modèle, considérez la fonction\(f(x)=x^2\) dont la dérivée est\(f′(x)=2x\) et non\(\dfrac{d}{dx}(x)⋅\dfrac{d}{dx}(x)=1⋅1=1.\)
Laisse\(f(x)\) et\(g(x)\) sois des fonctions différenciables. Alors
\[\dfrac{d}{dx}(f(x)g(x))=\dfrac{d}{dx}(f(x))⋅g(x)+\dfrac{d}{dx}(g(x))⋅f(x). \nonumber \]
C'est-à-dire
\[\text{if }p(x)=f(x)g(x),\quad \text{then }p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
Cela signifie que la dérivée d'un produit de deux fonctions est la dérivée de la première fonction multipliée par la deuxième fonction plus la dérivée de la deuxième fonction multipliée par la première fonction.
Nous commençons par supposer que\(f(x)\) et\(g(x)\) sont des fonctions dérivables. À un moment clé de cette preuve, nous devons utiliser le fait que, puisqu'elle\(g(x)\) est différenciable, elle est également continue. Nous tirons notamment parti du fait que, étant donné qu'elle\(g(x)\) est continue,\(\displaystyle \lim_{h→0}g(x+h)=g(x).\)
En appliquant la définition limite de la\(p(x)=f(x)g(x),\) dérivée à
\[ p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x)}{h}.\nonumber \]
En additionnant et\(f(x)g(x+h)\) en soustrayant dans le numérateur, nous avons
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Après avoir décomposé ce quotient et appliqué la loi de la somme pour les limites, la dérivée devient
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)}{h}+\lim_{h→0}\dfrac{f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
En réorganisant, nous obtenons
\ [\ begin {align*} p′ (x) &= \ lim_ {h→0} \ left (\ dfrac {f (x+h) −f (x)} {h} ⋅g (x+h) \ right) + \ lim_ {h→0} \ left (\ dfrac {g (x+h) −g (x)} {h} ⋅f (x) \ droite) \ \ [4pt]
&= \ left (\ lim_ {h→0} \ dfrac {f (x+h) −f (x)} {h} \ right) ⋅ \ left (\ lim_ {h→0} \ ; g (x+h) \ right) + \ left (\ lim_ {h→0} \ dfrac {g (x+h) −g (x)} {h} \ right) ⋅f (x) \ end {align*} \]
En utilisant la continuité\(g(x)\), la définition des dérivées de\(f(x)\) et et\(g(x)\) en appliquant les lois limites, nous arrivons à la règle du produit,
\[p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
□
Pour\(p(x)=f(x)g(x)\), utilisez la règle du produit pour déterminer\(p′(2)\) si\(f(2)=3,\; f′(2)=−4,\; g(2)=1\), et\(g′(2)=6\).
Solution
Depuis\(p(x)=f(x)g(x)\),\(p′(x)=f′(x)g(x)+g′(x)f(x),\) et donc
\(p′(2)=f′(2)g(2)+g′(2)f(2)=(−4)(1)+(6)(3)=14.\)
Pour\(p(x)=(x^2+2)(3x^3−5x),\) rechercher\(p′(x)\) en appliquant la règle du produit. Vérifiez le résultat en trouvant d'abord le produit, puis en le différenciant.
Solution
Si nous définissons\(f(x)=x^2+2\) et\(g(x)=3x^3−5x\), alors\(f′(x)=2x\) et\(g′(x)=9x^2−5\). Ainsi,
\(p′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3x^3−5x)+(9x^2−5)(x^2+2).\)
En simplifiant, nous avons
\[p′(x)=15x^4+3x^2−10. \nonumber \]
Pour vérifier, nous voyons que\(p(x)=3x^5+x^3−10x\) et, par conséquent,\(p′(x)=15x^4+3x^2−10.\)
Utilisez la règle du produit pour obtenir la dérivée de\(p(x)=2x^5(4x^2+x).\)
- Allusion
-
Définissez\(f(x)=2x^5\)\(g(x)=4x^2+x\) et utilisez l'exemple précédent comme guide.
- Réponse
-
\(p′(x)=10x^4(4x^2+x)+(8x+1)(2x^5)=56x^6+12x^5.\)
La règle du quotient
Après avoir développé et mis en pratique la règle du produit, nous envisageons maintenant de différencier les quotients des fonctions. Comme nous le voyons dans le théorème suivant, la dérivée du quotient n'est pas le quotient des dérivées ; c'est plutôt la dérivée de la fonction au numérateur multipliée par la fonction au dénominateur moins la dérivée de la fonction au dénominateur multipliée par la fonction au numérateur, le tout divisé par le carré de la fonction au dénominateur. Afin de mieux comprendre pourquoi nous ne pouvons pas simplement prendre le quotient des dérivées, gardez à l'esprit que
\[\dfrac{d}{dx}(x^2)=2x,\text{ not }\dfrac{\dfrac{d}{dx}(x^3)}{\dfrac{d}{dx}(x)}=\dfrac{3x^2}{1}=3x^2.\nonumber \]
Laisse\(f(x)\) et\(g(x)\) sois des fonctions différenciables. Alors
\[\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{dx}(f(x))⋅g(x)−\dfrac{d}{dx}(g(x))⋅f(x)}{\big(g(x)\big)^2}. \nonumber \]
Autrement dit, si
\[q(x)=\dfrac{f(x)}{g(x)}\nonumber \]
alors
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}.\nonumber \]
La règle de la preuve du quotient est très similaire à la règle de la preuve du produit, elle est donc omise ici. Nous appliquons plutôt cette nouvelle règle pour trouver des dérivés dans l'exemple suivant.
Utilisez la règle du quotient pour trouver la dérivée de\(q(x)=\dfrac{5x^2}{4x+3}.\)
Solution
Laissez\(f(x)=5x^2\) et\(g(x)=4x+3\). Ainsi,\(f′(x)=10x\) et\(g′(x)=4\).
En remplaçant la règle du quotient, nous avons
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{(g(x))^2}=\dfrac{10x(4x+3)−4(5x^2)}{(4x+3)^2}.\nonumber \]
En simplifiant, nous obtenons
\[q′(x)=\dfrac{20x^2+30x}{(4x+3)^2}\nonumber \]
Trouvez le dérivé de\(h(x)=\dfrac{3x+1}{4x−3}\).
- Allusion
-
Appliquez la règle du quotient avec\(f(x)=3x+1\) et\(g(x)=4x−3\).
- Réponse
-
\(h′(x)=−\dfrac{13}{(4x−3)^2}.\)
Il est désormais possible d'utiliser la règle du quotient pour étendre la règle de puissance afin de trouver des dérivées de fonctions de la forme\(x^k\) où\(k\) est un entier négatif.
Si\(k\) est un entier négatif, alors
\[\dfrac{d}{dx}(x^k)=kx^{k−1}. \nonumber \]
Si\(k\) est un entier négatif, on peut le définir\(n=−k\), de sorte que n soit un entier positif avec\(k=−n\). Puisque pour chaque entier positif\(n\)\(x^{−n}=\dfrac{1}{x^n}\), nous pouvons maintenant appliquer la règle du quotient en définissant\(f(x)=1\) et\(g(x)=x^n\). Dans ce cas,\(f′(x)=0\) et\(g′(x)=nx^{n−1}\). Ainsi,
\[\dfrac{d}{dx}(x^{−n})=\dfrac{0(x^n)−1(nx^{n−1})}{(x^n)^2}.\nonumber \]
En simplifiant, nous voyons que
\[\begin{align*} \dfrac{d}{dx}(x^{−n}) &=\dfrac{−nx^{n−1}}{x^{2n}}\\[4pt]&=−nx^{(n−1)−2n}\\[4pt]&=−nx^{−n−1}.\end{align*}\]
Enfin, notez que puisque\(k=−n\), en les substituant, nous avons
\[\dfrac{d}{dx}(x^k)=kx^{k−1}.\nonumber \]
□
Trouvez\(\dfrac{d}{dx}(x^{−4})\).
Solution
En appliquant la règle de puissance étendue avec\(k=−4\), nous obtenons
\[\dfrac{d}{dx}(x^{−4})=−4x^{−4−1}=−4x^{−5}.\nonumber \]
Utilisez la règle de puissance étendue et la règle des multiples constants pour trouver\(f(x)=\dfrac{6}{x^2}\).
Solution
Il peut sembler tentant d'utiliser la règle du quotient pour trouver cette dérivée, et il ne serait certainement pas incorrect de le faire. Cependant, il est beaucoup plus facile de différencier cette fonction en la réécrivant d'abord sous la forme\(f(x)=6x^{−2}\).
\ (\ begin {align*} f′ (x) &= \ dfrac {d} {dx} \ left (\ dfrac {6} {x^2} \ right) = \ dfrac {d} {dx} \ left (6x^ {−2} \ right) & \ text {Réécriture} \ dfrac {6} {x^2} \ text {en tant que 6} x^ {−2}. \ \ [4pt]
&=6 \ dfrac {d} {dx} \ left (x^ {−2} \ right) & & \ text {Appliquez la règle des multiples constants.} \ \ [4pt]
&=6 (−2x^ { −3}) & & \ text {Utilisez la règle de puissance étendue pour différencier} x^ {−2}. \ \ [4pt]
&=−12x^ {−3} & & \ text {Simplifier.} \ end {align*} \)
Déterminez la dérivée de\(g(x)=\dfrac{1}{x^7}\) l'utilisation de la règle de puissance étendue.
- Allusion
-
Réécrire\(g(x)=\dfrac{1}{x^7}=x^{−7}\). Utilisez la règle de puissance étendue avec\(k=−7\).
- Réponse
-
\(g′(x)=−7x^{−8}\).
Combinaison de règles de
Comme nous l'avons vu tout au long des exemples de cette section, il arrive rarement que nous soyons appelés à appliquer une seule règle de différenciation pour trouver la dérivée d'une fonction donnée. À ce stade, en combinant les règles de différenciation, nous pouvons trouver les dérivées de n'importe quelle fonction polynomiale ou rationnelle. Plus tard, nous rencontrerons des combinaisons plus complexes de règles de différenciation. Une bonne règle de base à utiliser lors de l'application de plusieurs règles consiste à appliquer les règles dans l'ordre inverse de celui dans lequel nous évaluerions la fonction.
Pour\(k(x)=3h(x)+x^2g(x)\), trouvez\(k′(x)\).
Solution : La recherche de cette dérivée nécessite la règle de la somme, la règle des multiples constants et la règle du produit.
| \(k′(x)=\dfrac{d}{dx}\big(3h(x)+x^2g(x)\big)=\dfrac{d}{dx}\big(3h(x)\big)+\dfrac{d}{dx}\big(x^2g(x)\big)\) | Appliquez la règle de la somme. |
| \(=3\dfrac{d}{dx}\big(h(x)\big)+\left(\dfrac{d}{dx}(x^2)g(x)+\dfrac{d}{dx}(g(x))x^2\right)\) | Appliquez la règle du multiple constant pour différencier\(3h(x)\) et la règle du produit pour différencier\(x^2g(x)\). |
| \(=3h′(x)+2xg(x)+g′(x)x^2\) |
Pour\(k(x)=f(x)g(x)h(x)\), exprimer\(k′(x)\) en termes de\(f(x),g(x),h(x)\), et leurs dérivés.
Solution
Nous pouvons considérer la fonction\(k(x)\) comme le produit de la fonction\(f(x)g(x)\) et de la fonction\(h(x)\). C'est-à-dire,\(k(x)=(f(x)g(x))⋅h(x)\). Ainsi,
\ (\ begin {align*} k′ (x) &= \ dfrac {d} {dx} \ big (f (x) g (x) \ big) ⋅h (x) + \ dfrac {d} {dx} \ big (h (x) \ big) ⋅ \ big (f (x) g (x) \ big). & & \ text {Appliquez la règle du produit au produit de} f (x) g (x) \ text {et} h (x). \ \ [4pt]
&= \ big (f′ (x) g (x) +g′ (x) f (x) \ big) h (x) +h′ (x) f (x) g (x) & & \ text {Appliquer la règle du produit à} f (x) g (x) \ \ [4 points]
&=f (x) g (x) h (x) +f (x) g′ (x) h (x) +f (x) g (x) h (x). & & \ text {Simplifier.} \ end {align*} \)
Pour\(h(x)=\dfrac{2x^3k(x)}{3x+2}\), trouvez\(h′(x)\).
Solution
Cette procédure est typique pour trouver la dérivée d'une fonction rationnelle.
\ (\ begin {align*} h′ (x) &= \ dfrac {\ dfrac {d} {dx} (2x^3k (x)) ⋅ (3x+2) − \ dfrac {d} {dx} (3x+2) ⋅ (2x^3k (x))} {(3x+2) ^2} & & \ text {Appliquez la règle du quotient.} \ \ [4pt]
&= \ dfrac {(6x^2k (x) +k′ (x) ⋅2x^3) (3x+2) −3 (2x^3k (x))} {(3x+2) ^2} & & \ text {Appliquez la règle du produit pour trouver} \ dfrac {d} {dx} (2x^3k (x)). \ text {Utilisation} \ dfrac {d} {dx} (3x+2) =3. \ \ [4pt]
&= \ dfrac {−6x^3k (x) +18x^3k (x) +12x^2k (x) +6x^4k′ (x) +4x^3k′ (x)} {(3x+2) ^2} & \ text {Simplifier} \ end {align*} \)
Trouvez\(\dfrac{d}{dx}(3f(x)−2g(x)).\)
- Allusion
-
Appliquez la règle des différences et la règle du multiple constant.
- Réponse
-
\(3f′(x)−2g′(x).\)
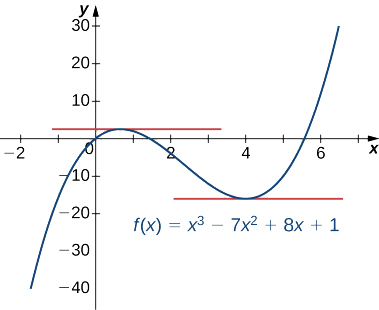
Déterminez les valeurs de\(x\) pour lesquelles\(f(x)=x^3−7x^2+8x+1\) possède une tangente horizontale.
Solution
Pour trouver les valeurs de\(x\) pour lesquelles\(f(x)\) a une tangente horizontale, nous devons résoudre\(f′(x)=0\).
Depuis\(f′(x)=3x^2−14x+8=(3x−2)(x−4)\),
nous devons résoudre ce problème\((3x−2)(x−4)=0\). Nous voyons donc que la fonction possède des lignes tangentes horizontales à\(x=\dfrac{2}{3}\) et,\(x=4\) comme indiqué dans le graphique suivant.
La position d'un objet sur un axe de coordonnées à un moment donné\(t\) est donnée par\(s(t)=\dfrac{t}{t^2+1}.\) Quelle est la vitesse initiale de l'objet ?
Solution
Puisque la vitesse initiale est,\(v(0)=s′(0),\) commencez\(s′(t)\) par déterminer en appliquant la règle du quotient :
\(s′(t)=\dfrac{1(t^2+1)−2t(t)}{(t^2+1)^2}=\dfrac{1−t^2}{(t^2+1)^2}\).
Après évaluation, nous constatons que\(v(0)=1.\)
Détermine les valeurs\(x\) pour lesquelles la droite tangente au graphe de\(f(x)=4x^2−3x+2\) possède une tangente parallèle à la droite\(y=2x+3.\)
- Allusion
-
Résoudre\(f′(x)=2\).
- Réponse
-
\(\dfrac{5}{8}\)
Les courses automobiles de Formule 1 peuvent être très excitantes à regarder et attirer de nombreux spectateurs. Les concepteurs de circuits de Formule 1 doivent veiller à ce que suffisamment d'espace en tribune soit disponible autour de la piste pour accueillir ces spectateurs. Cependant, les courses automobiles peuvent être dangereuses et les considérations de sécurité sont primordiales. Les tribunes doivent être placées à un endroit où les spectateurs ne seront pas en danger si le conducteur perd le contrôle de sa voiture (Figure\(\PageIndex{3}\)).

La sécurité est particulièrement préoccupante dans les virages. Si le conducteur ne ralentit pas suffisamment avant d'entrer dans le virage, la voiture risque de glisser hors de la piste de course. Normalement, cela se traduit par un virage plus large, ce qui ralentit le conducteur. Mais si le pilote perd complètement le contrôle, la voiture risque de quitter complètement la piste, sur une trajectoire tangente à la courbe du circuit.
Supposons que vous conceviez un nouveau circuit de Formule 1. Une section de la piste peut être modélisée par la fonction\(f(x)=x^3+3x^2+x\) (Figure\(\PageIndex{4}\)). Le plan actuel prévoit la construction de tribunes le long de la première ligne droite et autour d'une partie de la première courbe. Les plans prévoient que le coin avant de la tribune soit situé au point (\(−1.9,2.8\)). Nous voulons déterminer si cet emplacement met en danger les spectateurs en cas de perte de contrôle de la voiture par le conducteur.
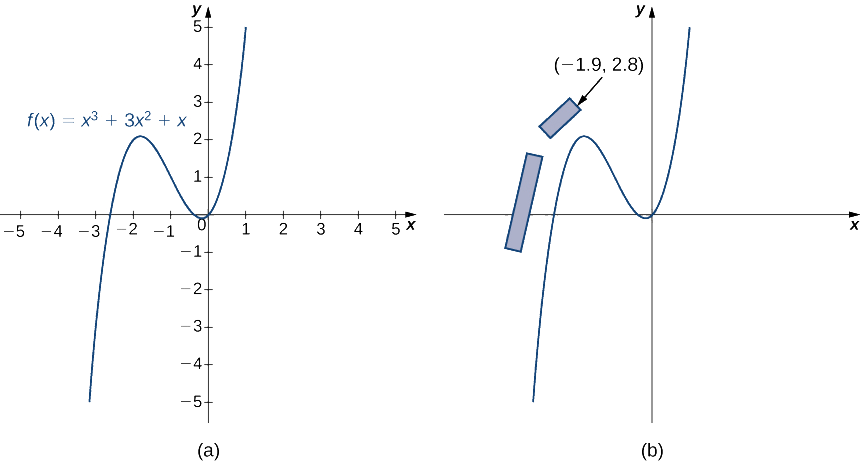
- Les physiciens ont déterminé que les conducteurs sont plus susceptibles de perdre le contrôle de leur voiture lorsqu'ils entrent dans un virage, au point où la pente de la tangente est de 1. Trouvez les\((x,y)\) coordonnées de ce point près du virage.
- Trouvez l'équation de la tangente à la courbe à ce point.
- Pour déterminer si les spectateurs sont en danger dans ce scénario, trouvez la\(x\) coordonnée du point où la tangente croise la ligne\(y=2.8\). Est-ce que ce point se trouve en toute sécurité à droite de la tribune ? Ou les spectateurs sont-ils en danger ?
- Et si un conducteur perd le contrôle plus tôt que ne le prévoient les physiciens ? Supposons qu'un conducteur perde le contrôle au point (\(−2.5,0.625\)). Quelle est la pente de la tangente à ce point ?
- Si un conducteur perd le contrôle comme décrit dans la partie 4, les spectateurs sont-ils en sécurité ?
- Devriez-vous poursuivre la conception actuelle de la tribune ou devriez-vous déplacer les tribunes ?
Concepts clés
- La dérivée d'une fonction constante est zéro.
- La dérivée d'une fonction de puissance est une fonction dans laquelle la puissance sous tension\(x\) devient le coefficient du terme et la puissance sur\(x\) la dérivée diminue de 1.
- La dérivée d'une constante\(c\) multipliée par une fonction\(f\) est identique à la constante multipliée par la dérivée.
- La dérivée de la somme d'une fonction\(f\) et d'une fonction\(g\) est identique à la somme de la dérivée de\(f\) et de la dérivée de\(g\).
- La dérivée de la différence entre une fonction\(f\) et une fonction\(g\) est identique à la différence entre la dérivée de\(f\) et la dérivée de\(g\).
- La dérivée d'un produit de deux fonctions est la dérivée de la première fonction multipliée par la seconde fonction plus la dérivée de la seconde fonction multipliée par la première fonction.
- La dérivée du quotient de deux fonctions est la dérivée de la première fonction multipliée par la deuxième fonction moins la dérivée de la deuxième fonction multipliée par la première fonction, le tout divisé par le carré de la deuxième fonction.
- Nous avons utilisé la définition limite du dérivé pour développer des formules qui nous permettent de trouver des dérivés sans avoir à recourir à la définition du dérivé. Ces formules peuvent être utilisées seules ou en combinaison les unes avec les autres.
Lexique
- règle multiple constante
- la dérivée d'une constante\(c\) multipliée par une fonction\(f\) est identique à la constante multipliée par la dérivée :\(\dfrac{d}{dx}\big(cf(x)\big)=cf′(x)\)
- règle constante
- la dérivée d'une fonction constante est zéro :\(\dfrac{d}{dx}(c)=0\), où\(c\) est une constante
- règle de différence
- la dérivée de la différence entre une fonction\(f\) et une fonction\(g\) est la même que la différence entre la dérivée\(f\) et la dérivée de\(g\) :\(\dfrac{d}{dx}\big(f(x)−g(x)\big)=f′(x)−g′(x)\)
- règle du pouvoir
- la dérivée d'une fonction de puissance est une fonction dans laquelle la puissance sous tension\(x\) devient le coefficient du terme et la puissance sur\(x\) la dérivée diminue de 1 : Si\(n\) est un entier, alors\(\dfrac{d}{dx}\left(x^n\right)=nx^{n−1}\)
- règle du produit
- la dérivée d'un produit de deux fonctions est la dérivée de la première fonction multipliée par la deuxième fonction plus la dérivée de la deuxième fonction multipliée par la première fonction :\(\dfrac{d}{dx}\big(f(x)g(x)\big)=f′(x)g(x)+g′(x)f(x)\)
- règle du quotient
- la dérivée du quotient de deux fonctions est la dérivée de la première fonction multipliée par la deuxième fonction moins la dérivée de la deuxième fonction multipliée par la première fonction, le tout divisé par le carré de la deuxième fonction :\(\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}\)
- règle de somme
- la dérivée de la somme d'une fonction\(f\) et d'une fonction\(g\) est identique à la somme de la dérivée\(f\) et de la dérivée de\(g\) :\(\dfrac{d}{dx}\big(f(x)+g(x)\big)=f′(x)+g′(x)\)


