2.4 : Continuité

Last updated
Save as PDF

Page ID: 197991

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Expliquez les trois conditions de continuité à un moment donné.
Décrivez trois types de discontinuités.
Définissez la continuité sur un intervalle.
Énoncez le théorème des limites des fonctions composites.
Donnez un exemple du théorème des valeurs intermédiaires.

De nombreuses fonctions ont la propriété de pouvoir tracer leurs graphes avec un crayon sans lever le crayon de la page. Ces fonctions sont appelées continues. D'autres fonctions comportent des points où se produit une rupture du graphe, mais satisfont à cette propriété sur les intervalles contenus dans leurs domaines. Ils sont continus sur ces intervalles et sont censés présenter une discontinuité au point où une rupture se produit.

Nous commençons notre étude de la continuité en explorant ce que signifie pour une fonction le fait d'avoir une continuité à un moment donné. Intuitivement, une fonction est continue à un point donné s'il n'y a pas de rupture dans son graphe à ce point.

Continuité à un moment donné

Avant d'examiner une définition formelle de ce que signifie pour une fonction le fait d'être continue à un moment donné, examinons diverses fonctions qui ne répondent pas à notre conception intuitive de ce que signifie être continue à un moment donné. Nous créons ensuite une liste de conditions qui empêchent de telles défaillances.

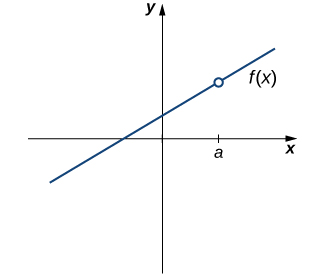
Notre première fonction intéressante est illustrée dans la figure\(\PageIndex{1}\). Nous voyons que le graphique de\(f(x)\) a un trou à\(a\). En fait,\(f(a)\) n'est pas défini. À tout le moins, pour\(f(x)\) être continu à\(a\), nous avons besoin de la condition suivante :

i.\(f(a)\) est défini

Un graphique d'une fonction linéaire croissante f (x) qui traverse l'axe des x du quadrant trois au quadrant deux et qui traverse l'axe des y du quadrant deux au quadrant un. Un point a supérieur à zéro est marqué sur l'axe des x. Le point de la fonction f (x) au-dessus de a est un cercle ouvert ; la fonction n'est pas définie en a. — Figure\(\PageIndex{1}\) : La fonction n'\(f(x)\)est pas continue\(a\) car elle n'\(f(a)\)est pas définie.

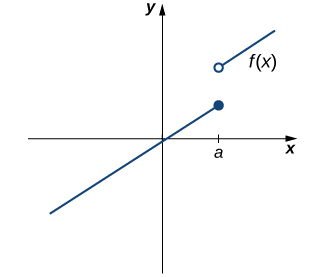
Cependant, comme nous le voyons sur la figure\(\PageIndex{2}\), cette condition à elle seule ne suffit pas à garantir la continuité sur le point\(a\). Bien\(f(a)\) que définie, la fonction présente un écart de\(a\). Dans cet exemple, l'écart existe parce qu'il\(\displaystyle \lim_{x→a}f(x)\) n'existe pas. Nous devons ajouter une autre condition de continuité à\(a\)... à savoir,

ii. \(\displaystyle \lim_{x→a}f(x)\)existe

Le graphe d'une fonction f (x) par morceaux en deux parties. La première partie est une fonction linéaire croissante qui passe du quadrant trois au quadrant un à l'origine. Un point a supérieur à zéro est marqué sur l'axe des x. À fa. sur ce segment, il y a un cercle plein. L'autre segment est également une fonction linéaire croissante. Il existe dans le premier quadrant pour les valeurs de x supérieures à a. À x=a, ce segment possède un cercle ouvert. — Figure\(\PageIndex{2}\) : La fonction n'\(f(x)\)est pas continue\(a\) car elle\(\displaystyle \lim_{x→a}f(x)\) n'existe pas.

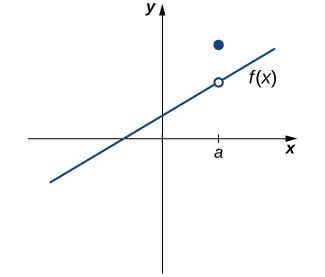
Cependant, comme nous le voyons sur la figure\(\PageIndex{3}\), ces deux conditions à elles seules ne garantissent pas la continuité à un moment donné. La fonction de cette figure satisfait à nos deux premières conditions, mais n'est toujours pas continue à\(a\). Nous devons ajouter une troisième condition à notre liste :

iii. \(\displaystyle \lim_{x→a}f(x)=f(a)\)

Le graphique d'une fonction par morceaux en deux parties. La première partie est une fonction linéaire croissante qui traverse l'axe x du quadrant trois au quadrant deux et qui traverse l'axe y du quadrant deux au quadrant un. Un point a supérieur à zéro est marqué sur l'axe des x. À ce stade, il y a un cercle ouvert sur la fonction linéaire. La deuxième partie est un point situé à x=a au-dessus de la ligne. — Figure\(\PageIndex{3}\) : La fonction n'\(f(x)\)est pas continue à\(a\) cause de\(\displaystyle \lim_{x→a}f(x)≠f(a)\).

Nous rassemblons maintenant notre liste de conditions et établissons une définition de la continuité à un moment donné.

Définition : Continu à un point

Une fonction\(f(x)\) est continue à un point donné \(a\)si et seulement si les trois conditions suivantes sont satisfaites :

\(f(a)\)est défini
\(\displaystyle \lim_{x→a}f(x)\)existe
\(\displaystyle \lim_{x→a}f(x)=f(a)\)

Une fonction est discontinue à un point\(a\) si elle n'est pas continue à\(a\).

La procédure suivante peut être utilisée pour analyser la continuité d'une fonction à un point en utilisant cette définition.

Stratégie de résolution de problèmes : déterminer la continuité à un moment donné

Vérifiez si elle\(f(a)\) est définie. Si\(f(a)\) ce n'est pas défini, il n'est pas nécessaire d'aller plus loin. La fonction n'est pas continue\(a.\) lorsque Si elle\(f(a)\) est définie, passez à l'étape 2.
Calculer\(\displaystyle \lim_{x→a}f(x)\). Dans certains cas, nous pouvons avoir besoin de le faire en calculant d'abord\(\displaystyle \lim_{x→a^−}f(x)\) et\(\displaystyle \lim_{x→a^+}f(x)\). Si elle\(\displaystyle \lim_{x→a}f(x)\) n'existe pas (c'est-à-dire qu'il ne s'agit pas d'un nombre réel), la fonction n'est pas continue\(a\) et le problème est résolu. Si\(\displaystyle \lim_{x→a}f(x)\) tel est le cas, passez à l'étape 3.
Comparez\(f(a)\) et\(\displaystyle \lim_{x→a}f(x)\). Si\(\displaystyle \lim_{x→a}f(x)≠f(a)\), alors la fonction n'est pas continue à\(a.\) If\(\displaystyle \lim_{x→a}f(x)=f(a)\), alors la fonction est continue à\(a.\)

Les trois exemples suivants montrent comment appliquer cette définition pour déterminer si une fonction est continue à un point donné. Ces exemples illustrent des situations dans lesquelles chacune des conditions de continuité de la définition réussit ou échoue.

Exemple\(\PageIndex{1A}\): Determining Continuity at a Point, Condition 1

À l'aide de la définition, déterminez si la fonction\(f(x)=\dfrac{x^2−4}{x−2}\) est continue à\(x=2\). Justifiez la conclusion.

Solution

Commençons par essayer de calculer\(f(2)\). Nous pouvons le constater\(f(2)=0/0\), ce qui n'est pas défini. Par conséquent,\(f(x)=\dfrac{x^2−4}{x−2}\) est discontinu à\(2\) parce qu'il n'\(f(2)\)est pas défini. Le graphique de\(f(x)\) est illustré sur la figure\(\PageIndex{4}\).

Un graphique de la fonction donnée. Il y a une droite qui traverse l'axe x du quadrant trois au quadrant deux et qui traverse l'axe des y du quadrant deux au quadrant un. À un point du premier quadrant, il y a un cercle ouvert où la fonction n'est pas définie. — Figure\(\PageIndex{4}\) : La fonction\(f(x)\) est discontinue\(2\) car elle n'\(f(2)\)est pas définie.

Exemple\(\PageIndex{1B}\): Determining Continuity at a Point, Condition 2

À l'aide de la définition, déterminez si la fonction\(f(x)=\begin{cases}−x^2+4, & \mathrm{if} \; x≤3 \\ 4x−8, & \mathrm{if} \; x>3\end{cases}\) est continue à\(x=3\). Justifiez la conclusion.

Solution

Commençons par essayer de calculer\(f(3)\).

\(f(3)=−(3^2)+4=−5\).

Ainsi,\(f(3)\) est défini. Ensuite, nous calculons\(\displaystyle \lim_{x→3}f(x)\). Pour cela, il faut calculer\(\displaystyle \lim_{x→3^−}f(x)\) et\( \displaystyle \lim_{x→3^+}f(x)\) :

\(\displaystyle \lim_{x→3^−}f(x)=−(3^2)+4=−5\)

\(\displaystyle \lim_{x→3^+}f(x)=4(3)−8=4\).

Par conséquent,\(\displaystyle \lim_{x→3}f(x)\) n'existe pas. Ainsi, n'\(f(x)\)est pas continu à 3. Le graphique de\(f(x)\) est illustré sur la figure\(\PageIndex{5}\).

Un graphique de la fonction par morceaux donnée, qui comporte deux parties. La première est une parabole s'ouvrant vers le bas qui est symétrique par rapport à l'axe y. Son sommet se trouve sur l'axe y, supérieur à zéro. Il y a un cercle fermé sur la parabole pour x=3. La deuxième partie est une fonction linéaire croissante dans le premier quadrant, qui existe pour des valeurs de x — Figure\(\PageIndex{5}\) : La fonction n'\(f(x)\)est pas continue à 3 car\(\displaystyle \lim_{x→3}f(x)\) elle n'existe pas.

Exemple\(\PageIndex{1C}\): Determining Continuity at a Point, Condition 3

À l'aide de la définition, déterminez si la fonction\(f(x)=\begin{cases}\frac{\sin x}{x}, & \text{if } x≠0\\1, & \text{if } x=0\end{cases}\) est continue à\(x=0\).

Solution

Tout d'abord, observez que

\(f(0)=1\)

Ensuite,

\(\displaystyle \lim_{x→0}f(x)=\lim_{x→0}\frac{\sin x}{x}=1\).

Enfin, comparez\(f(0)\) et\(\displaystyle \lim_{x→0}f(x)\). Nous voyons que

\(\displaystyle f(0)=1=\lim_{x→0}f(x)\).

Puisque les trois conditions de la définition de la continuité sont satisfaites,\(f(x)\) est continue à\(x=0\).

Exercice\(\PageIndex{1}\)

À l'aide de la définition, déterminez si la fonction\(f(x)=\begin{cases}2x+1, & \text{if }x<1\\2, & \text{if }x=1\\ −x+4, & \text{if }x>1\end{cases}\) est continue à\(x=1\). Si la fonction n'est pas continue à 1, indiquez la condition de continuité à un point qui ne tient pas.

Allusion: Vérifiez chaque condition de la définition.

Réponse: \(f\)n'est pas continu à\(1\) parce que\(\displaystyle f(1)=2≠3=\lim_{x→1}f(x)\).

En appliquant la définition de la continuité et les théorèmes précédemment établis concernant l'évaluation des limites, nous pouvons énoncer le théorème suivant.

Théorème\(\PageIndex{1}\): Continuity of Polynomials and Rational Functions

Les polynômes et les fonctions rationnelles sont continus en tout point de leurs domaines.

Une preuve

Auparavant, nous avons montré que si\(p(x)\) et\(q(x)\) sont des polynômes,\(\displaystyle \lim_{x→a}p(x)=p(a)\) pour chaque polynôme\(p(x)\) et\(\displaystyle \lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}\) aussi longtemps que\(q(a)≠0\). Par conséquent, les polynômes et les fonctions rationnelles sont continus sur leurs domaines.

□

Nous appliquons maintenant le théorème\(\PageIndex{1}\) pour déterminer les points où une fonction rationnelle donnée est continue.

Exemple\(\PageIndex{2}\):Continuity of a Rational Function

Pour quelles valeurs de x est\(f(x)=\dfrac{x+1}{x−5}\) continue ?

Solution

La fonction rationnelle\(f(x)=\dfrac{x+1}{x−5}\) est continue pour chaque valeur de\(x\) except\(x=5\).

Exercice\(\PageIndex{2}\)

Pour quelles valeurs de\(x\) est\(f(x)=3x^4−4x^2\) continu ?

Allusion: Utilisez la continuité des polynômes et des fonctions rationnelles indiquées ci-dessus.

Réponse: \(f(x)\)est continu à chaque nombre réel.

Types de discontinuités

Comme nous l'avons vu dans Example\(\PageIndex{1A}\) et Example\(\PageIndex{1B}\), les discontinuités prennent plusieurs apparences différentes. Nous classons les types de discontinuités que nous avons observés jusqu'à présent comme des discontinuités amovibles, des discontinuités infinies ou des discontinuités de saut. Intuitivement, une discontinuité amovible est une discontinuité pour laquelle il existe un trou dans le graphique, une discontinuité de saut est une discontinuité non infinie pour laquelle les sections de la fonction ne se rejoignent pas, et une discontinuité infinie est une discontinuité située au niveau d'un asymptote verticale. La figure\(\PageIndex{6}\) illustre les différences entre ces types de discontinuités. Bien que ces termes fournissent un moyen pratique de décrire trois types courants de discontinuités, gardez à l'esprit que toutes les discontinuités ne rentrent pas parfaitement dans ces catégories.

Trois graphiques, chacun montrant une discontinuité différente. La première est la discontinuité amovible. Ici, la fonction donnée est une droite à pente positive. Au point x=a, où a — Figure\(\PageIndex{6}\) : Les discontinuités sont classées comme (a) amovibles, (b) sauteuses ou (c) infinies.

Ces trois discontinuités sont formellement définies comme suit :

Définition

Si\(f(x)\) c'est discontinu à ce\(a,\) moment-là

1. \(f\)présente une discontinuité amovible\(a\) s'\(\displaystyle \lim_{x→a}f(x)\)il existe. (Remarque : lorsque nous affirmons qu'\(\displaystyle \lim_{x→a}f(x)\)il existe, nous voulons dire cela\(\displaystyle \lim_{x→a}f(x)=L\), où\(L\) se trouve un nombre réel.)

2. \(f\)a une discontinuité de saut à\(a\) si\(\displaystyle \lim_{x→a^−}f(x)\) et\(\displaystyle \lim_{x→a^+}f(x)\) les deux existent, mais\(\displaystyle \lim_{x→a^−}f(x)≠lim_{x→a^+}f(x)\). (Remarque : lorsque nous affirmons que\(\displaystyle \lim_{x→a^−}f(x)\) les\(\displaystyle \lim_{x→a^+}f(x)\) deux existent, nous voulons dire que les deux ont une valeur réelle et qu'aucune des deux n'assume les valeurs\(±∞\).)

3. \(f\)présente une discontinuité infinie à\(a\) if\(\displaystyle \lim_{x→a^−}f(x)=±∞\) ou\(\displaystyle \lim_{x→a^+}f(x)=±∞\).

Exemple\(\PageIndex{3}\): Classifying a Discontinuity

Dans l'exemple,\(\PageIndex{1A},\) nous avons montré que\(f(x)=\dfrac{x^2−4}{x−2}\) c'est discontinu à\(x=2\). Classez cette discontinuité comme amovible, sauteuse ou infinie.

Solution

Pour classer la discontinuité chez,\(2\) nous devons évaluer\(\displaystyle \lim_{x→2}f(x)\) :

\ (\ displaystyle \ begin {align*} \ lim_ {x→2} f (x) &= \ lim_ {x→2} \ frac {x^2−4} {x−2} \ \ [4 points]
&= \ lim_ {x→2} \ frac {(x−2) (x+2)} {x−2} \ \ [4 points]
&= \ lim_ {x→2} (x+2) \ \ [4 points]
&=4. \ end {align*} \)

Puisque\(f\) est discontinu à\(2\) et\(\displaystyle \lim_{x→2}f(x)\) existe,\(f\) a une discontinuité amovible à\(x=2\).

Exemple\(\PageIndex{4}\): Classifying a Discontinuity

Dans l'exemple\(\PageIndex{1B}\), nous avons montré que\(f(x)=\begin{cases}−x^2+4, &\text{if }x≤3\\4x−8, &\text{if }x>3\end{cases}\) c'est discontinu à\(x=3\). Classez cette discontinuité comme amovible, sauteuse ou infinie.

Solution

Plus tôt, nous avons montré que\(f\) c'est discontinu\(3\) parce que\(\displaystyle \lim_{x→3}f(x)\) cela n'existe pas. Cependant, étant donné que\(\displaystyle \lim_{x→3^−}f(x)=−5\) les\(\displaystyle \lim_{x→3^+}f(x)=4\) deux existent, nous concluons que la fonction présente une discontinuité de saut à\(3\).

Exemple\(\PageIndex{5}\): Classifying a Discontinuity

Déterminez s'il\(f(x)=\dfrac{x+2}{x+1}\) est continu à\(−1\). Si la fonction est discontinue à\(−1\), classez la discontinuité comme amovible, sauteuse ou infinie.

Solution

La valeur de la fonction n'\(f(−1)\)est pas définie. Par conséquent, la fonction n'est pas continue à\(−1\). Pour déterminer le type de discontinuité, nous devons déterminer la limite à\(−1\). Nous voyons cela\(\displaystyle \lim_{x→−1^−}\frac{x+2}{x+1}=−∞\) et\(\displaystyle \lim_{x→−1^+}\frac{x+2}{x+1}=+∞\). Par conséquent, la fonction présente une discontinuité infinie à\(−1\).

Exercice\(\PageIndex{3}\)

Pour\(f(x)=\begin{cases}x^2, &\text{if }x≠1\\3, & \text{if }x=1\end{cases}\), décidez si\(f\) c'est continu à\(1\). Si elle n'\(f\)est pas continue à\(1\), classez la discontinuité comme amovible, sauteuse ou infinie.

Allusion: Examinez les définitions des différents types de discontinuité énoncées ci-dessus. Si la fonction est discontinue à\(1\), regardez\(\displaystyle \lim_{x→1}f(x)\)

Réponse: Tapis discontinu\(1\) ; amovible

Continuité sur un intervalle

Maintenant que nous avons exploré le concept de continuité à un moment donné, nous étendons cette idée à la continuité sur un intervalle. Au fur et à mesure que nous développons cette idée pour différents types d'intervalles, il peut être utile de garder à l'esprit l'idée intuitive selon laquelle une fonction est continue sur un intervalle si nous pouvons utiliser un crayon pour tracer la fonction entre deux points de l'intervalle sans lever le crayon du papier. Pour nous préparer à définir la continuité sur un intervalle, nous commençons par examiner la définition de ce que signifie pour une fonction le fait d'être continue depuis la droite en un point et continue depuis la gauche en un point.

Définition : Continuité depuis la droite et depuis la gauche

On dit qu'une fonction\(f(x)\) est continue à partir de la droite à\(a\) if\(\displaystyle \lim_{x→a^+}f(x)=f(a)\).

Une fonction\(f(x)\) est dite continue à partir de la gauche à l'endroit\(a\) où\(\displaystyle \lim_{x→a^−}f(x)=f(a)\)

Une fonction est continue sur un intervalle ouvert si elle est continue à chaque point de l'intervalle. Une fonction\(f(x)\) est continue sur un intervalle fermé du formulaire\([a,b]\) si elle est continue à chaque point d'entrée, si elle est continue depuis la droite vers\(a\) et si elle est continue depuis la gauche sur. De\(b.\) manière analogue, une fonction\(f(x)\) est continue sur un intervalle du formulaire\((a,b)\) \((a,b]\)s'il est continu\((a,b)\) et s'il est continu à partir de la gauche, à\(b.\) Continuité sur d'autres types d'intervalles sont définis de la même manière.

Cela nous\(\displaystyle \lim_{x→b^−}f(x)=f(b)\) permet\(\displaystyle \lim_{x→a^+}f(x)=f(a)\) de tracer le graphique de la fonction d'un point\((a,f(a))\) à l'autre\((b,f(b))\) sans lever le crayon. Si, par exemple\(\displaystyle \lim_{x→a^+}f(x)≠f(a)\), nous devions lever notre crayon pour\(f(a)\) passer du graphique du reste de la fonction\((a,b]\).

Exemple\(\PageIndex{6}\): Continuity on an Interval

Indiquez le ou les intervalles pendant lesquels la fonction\(f(x)=\dfrac{x−1}{x^2+2x}\) est continue.

Solution

Comme il\(f(x)=\dfrac{x−1}{x^2+2x}\) s'agit d'une fonction rationnelle, elle est continue en tout point de son domaine. Le domaine de\(f(x)\) est l'ensemble\((−∞,−2)∪(−2,0)∪(0,+∞)\). Ainsi,\(f(x)\) est continu sur chacun des intervalles\((−∞,−2),(−2,0)\), et\((0,+∞)\).

Exemple\(\PageIndex{7}\): Continuity over an Interval

Indiquez le ou les intervalles pendant lesquels la fonction\(f(x)=\sqrt{4−x^2}\) est continue.

Solution

Grâce aux lois limites, nous le savons\(\displaystyle \lim_{x→a}\sqrt{4−x^2}=\sqrt{4−a^2}\) pour toutes les valeurs d'une entrée\((−2,2)\). Nous savons également que cela\(\displaystyle \lim_{x→−2^+}\sqrt{4−x^2}=0\) existe et\(\displaystyle \lim_{x→2^−}\sqrt{4−x^2}=0\) existe. Par conséquent,\(f(x)\) est continu sur l'intervalle\([−2,2]\).

Exercice\(\PageIndex{4}\)

Indiquez le ou les intervalles pendant lesquels la fonction\(f(x)=\sqrt{x+3}\) est continue.

Allusion: Utilisez Example\(\PageIndex{7}\) comme guide.

Réponse: \([−3,+∞)\)

\(\PageIndex{2}\)Le théorème nous permet d'étendre notre capacité à calculer des limites. En particulier, ce théorème nous permet finalement de démontrer que les fonctions trigonométriques sont continues dans leurs domaines.

Théorème\(\PageIndex{2}\): Composite Function Theorem

Si\(f(x)\) c'est continu à\(L\) et\(\displaystyle \lim_{x→a}g(x)=L\), alors

\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L).\)

Avant de passer à l'exemple,\(\PageIndex{8},\) rappelons que plus tôt, dans la section sur les lois limites, nous avons montré\(\displaystyle \lim_{x→0}\cos x=1=\cos(0)\). Par conséquent, nous savons que cela\(f(x)=\cos x\) se poursuit à\(0\). Dans l'exemple,\(\PageIndex{8},\) nous voyons comment combiner ce résultat avec le théorème de la fonction composite.

Exemple\(\PageIndex{8}\): Limit of a Composite Cosine Function

Évaluer\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)\).

Solution

La fonction donnée est composée de\(\cos x\) et\(x−\frac{π}{2}\). Puisque\(\displaystyle \lim_{x→π/2}\left(x−\frac{π}{2}\right)=0\) et\(\cos x\) est continu à\(0\), nous pouvons appliquer le théorème de la fonction composite. Ainsi,

\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)=\cos\left(\lim_{x→π/2}\left(x−\frac{π}{2}\right)\right)=\cos(0)=1.\)

Exercice\(\PageIndex{4}\):

Évaluer\(\displaystyle \lim_{x→π}\sin(x−π)\).

Allusion: \(f(x)=\sin x\)est continu à\(0\). Utilisez Example\(\PageIndex{8}\) comme guide.

Réponse: \(0\)

La preuve du théorème suivant utilise le théorème des fonctions composites ainsi que la continuité\(f(x)=\sin x\) et\(g(x)=\cos x\) au point\(0\) pour montrer que les fonctions trigonométriques sont continues sur l'ensemble de leurs domaines.

Théorème\(\PageIndex{3}\): Continuity of Trigonometric Functions

Les fonctions trigonométriques sont continues sur l'ensemble de leurs domaines.

Une preuve

Nous commençons par démontrer que\(\cos x\) c'est continu à chaque nombre réel. Pour ce faire, nous devons le montrer\(\displaystyle \lim_{x→a}\cos x=\cos a\) pour toutes les valeurs de\(a\).

\ (\ displaystyle \ begin {align*} \ lim_ {x→a} \ cos x &= \ lim_ {x→a} \ cos ((x−a) +a) & & \ text {Réécriture} x=x−a+a. \ \ [4 points]
&= \ lim_ {x→a} (\ cos (x−a) \ cos a− \ sin (x−a) \ sin a) & & \ text {Applique l'identité du cosinus de la somme de deux angles.} \ \ [4pt]
&= \ cos (\ lim_ {x→a} (x−a) )) \ cos a− \ sin (\ lim_ {x→a)) \ sin a & \ text {Depuis} \ lim_ {x→a} (x−a) =0, \ text {et} \ sin x \ text {et} \ cos x \ text {sont continus à} 0. \ \ [4 points]
&= \ cos (0) \ cos (0) \ cos a− \ sin (0)) \ sin a & \ text {Évaluez} \ cos (0) \ text {et} \ sin (0) \ text {et simplifiez.} \ \ [4 points]
&= 1⋅ \ cos a −0⋅ \ sin a= \ cos a. \ end {align*} \)

La preuve qui\(\sin x\) est continue à chaque nombre réel est analogue. Comme les fonctions trigonométriques restantes peuvent être exprimées en termes de\(\sin x\) et\(\cos x\), leur continuité découle de la loi des limites du quotient.

□

Comme vous pouvez le constater, le théorème des fonctions composites est inestimable pour démontrer la continuité des fonctions trigonométriques. Alors que nous poursuivons notre étude du calcul, nous revoyons ce théorème à de nombreuses reprises.

Le théorème de la valeur intermédiaire

Les fonctions qui sont continues sur des intervalles de la forme\([a,b]\), où\(a\) et\(b\) sont des nombres réels, présentent de nombreuses propriétés utiles. Tout au long de notre étude du calcul, nous rencontrerons de nombreux théorèmes puissants concernant de telles fonctions. Le premier de ces théorèmes est le théorème des valeurs intermédiaires.

Le théorème des valeurs intermédiaires

Laissez\(f\) être continus sur un intervalle fermé et limité\([a,b]\). S'il s'\(z\)agit d'un nombre réel compris entre\(f(a)\) et\(f(b)\), alors il y a un nombre\([a,b]\) satisfaisant\(c\)\(f(c)=z\) dans la figure\(\PageIndex{7}\).

Exemple\(\PageIndex{9}\): Application of the Intermediate Value Theorem

Afficher qui\(f(x)=x−\cos x\) possède au moins un zéro.

Solution

Comme\(f(x)=x−\cos x\) est continu\((−∞,+∞)\), il est continu sur n'importe quel intervalle fermé du formulaire\([a,b]\). Si vous pouvez trouver un intervalle\([a,b]\) tel que\(f(a)\) et que vous\(f(b)\) avez des signes opposés, vous pouvez utiliser le théorème des valeurs intermédiaires pour conclure\((a,b)\) qu'il doit y avoir un nombre\(c\) réel satisfaisant\(f(c)=0\). Notez que

\(f(0)=0−\cos(0)=−1<0\)

\(f(\frac{π}{2})=\frac{π}{2}−\cos\frac{π}{2}=\frac{π}{2}>0\).

En utilisant le théorème des valeurs intermédiaires, nous pouvons voir qu'il doit y avoir un nombre\(c\) réel\([0,π/2]\) qui satisfait\(f(c)=0\). Par conséquent,\(f(x)=x−\cos x\) possède au moins un zéro.

Exemple\(\PageIndex{10}\): When Can You Apply the Intermediate Value Theorem?

Si\(f(x)\) c'est continu\([0,2],f(0)>0\) et\(f(2)>0\), pouvons-nous utiliser le théorème des valeurs intermédiaires pour conclure qu'il n'y\(f(x)\) a pas de zéros dans l'intervalle\([0,2]\) ? Expliquez.

Solution

Non. Le théorème des valeurs intermédiaires nous permet uniquement de conclure que nous pouvons trouver une valeur entre\(f(0)\) et\(f(2)\) ; il ne nous permet pas de conclure que nous ne pouvons pas trouver d'autres valeurs. Pour y voir plus clair, considérez la fonction\(f(x)=(x−1)^2\). Cela satisfait\(f(0)=1>0,f(2)=1>0\), et\(f(1)=0\).

Exemple\(\PageIndex{11}\): When Can You Apply the Intermediate Value Theorem?

Pour\(f(x)=1/x,f(−1)=−1<0\) et\(f(1)=1>0\). Pouvons-nous en conclure qu'il y\(f(x)\) a un zéro dans l'intervalle\([−1,1]\) ?

Solution

Non. La fonction n'est pas continue\([−1,1]\). Le théorème des valeurs intermédiaires ne s'applique pas ici.

Exercice\(\PageIndex{5}\)

Afficher qui\(f(x)=x^3−x^2−3x+1\) possède un zéro sur l'intervalle\([0,1]\).

Allusion: Trouvez\(f(0)\) et\(f(1)\). Appliquez le théorème des valeurs intermédiaires.

Réponse: \(f(0)=1>0,\;f(1)=−2<0;\;f(x)\)est continu\([0,1]\). Il doit y avoir un zéro sur cet intervalle.

Concepts clés

Pour qu'une fonction soit continue en un point, elle doit être définie à ce point, sa limite doit exister au point et la valeur de la fonction à ce point doit être égale à la valeur de la limite à ce point.
Les discontinuités peuvent être classées comme amovibles, sauteuses ou infinies.
Une fonction est continue sur un intervalle ouvert si elle est continue à chaque point de l'intervalle. Il est continu sur un intervalle fermé s'il est continu en tout point de son intérieur et continu à ses extrémités.
Le théorème de la fonction composite indique : Si\(f(x)\) est continu en L et\(\displaystyle \lim_{x→a}g(x)=L\), alors\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L)\).

Le théorème des valeurs intermédiaires garantit que si une fonction est continue sur un intervalle fermé, elle prend toutes les valeurs comprises entre les valeurs de ses extrémités.

Lexique

continuité à un point: Une fonction\(f(x)\) est continue à un point donné\(a\) si et seulement si les trois conditions suivantes sont satisfaites : (1)\(f(a)\) est définie, (2)\(\displaystyle \lim_{x→a}f(x)\) existe et (3)\(\displaystyle \lim{x→a}f(x)=f(a)\)

continuité depuis la gauche: Une fonction est continue depuis la gauche à l'adresse\(b\) if\(\displaystyle \lim_{x→b^−}f(x)=f(b)\)

continuité depuis la droite: Une fonction est continue à partir de la droite à l'adresse\(a\) if\(\displaystyle \lim_{x→a^+}f(x)=f(a)\)

continuité sur un intervalle: une fonction qui peut être tracée au crayon sans lever le crayon ; une fonction est continue sur un intervalle ouvert si elle est continue à chaque point de l'intervalle ; une fonction\(f(x)\) est continue sur un intervalle fermé de la forme [\(a,b\)] si elle est continue à chaque point de (\(a,b\)), et il est continu de la droite vers\(a\) et de la gauche vers\(b\)

discontinuité à un point: Une fonction est discontinue en un point ou présente une discontinuité en un point si elle n'est pas continue en ce point

discontinuité infinie: Une discontinuité infinie se produit à un point\(a\) si\(\displaystyle \lim_{x→a^−}f(x)=±∞\) ou\(\displaystyle \lim_{x→a^+}f(x)=±∞\)

Théorème des valeurs intermédiaires: \(f\)Soyons continus sur un intervalle fermé [\(a,b\)] s'il s'\(z\)agit d'un nombre réel compris entre\(f(a)\) et\(f(b)\), alors il y a un nombre\(c\) dans [\(a,b\)] satisfaisant\(f(c)=z\)

discontinuité des sauts: Une discontinuité de saut se produit à un point\(a\) si\(\displaystyle \lim_{x→a^−}f(x)\) les\(\displaystyle \lim_{x→a^+}f(x)\) deux existent, mais\(\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)\)

discontinuité amovible: Une discontinuité amovible se produit à un point\(a\) si elle\(f(x)\) est discontinue à\(a\), mais\(\displaystyle \lim_{x→a}f(x)\) existe