2.1 : Un aperçu du calcul

Last updated
Save as PDF

Page ID: 197955

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Décrivez le problème tangent et comment il a conduit à l'idée d'une dérivée.
Expliquez comment l'idée d'une limite intervient dans la résolution du problème tangent.
Reconnaissez une tangente à une courbe en un point comme étant la limite des droites sécantes.
Identifiez la vitesse instantanée comme étant la limite de la vitesse moyenne sur un petit intervalle de temps.
Décrivez le problème de la zone et comment il a été résolu par l'intégrale.
Expliquez comment l'idée d'une limite intervient dans la résolution du problème de zone.
Reconnaissez comment les idées de limite, de dérivée et d'intégrale ont mené à l'étude des séries infinies et du calcul multivariable.

Alors que nous entamons notre étude du calcul, nous verrons comment son développement est né de solutions communes à des problèmes pratiques dans des domaines tels que la physique de l'ingénierie, comme le problème des voyages dans l'espace posé dans l'ouverture du chapitre. Deux problèmes clés ont conduit à la formulation initiale du calcul : (1) le problème de tangente, ou comment déterminer la pente d'une droite tangente à une courbe en un point ; et (2) le problème de surface, ou comment déterminer l'aire sous une courbe.

Le problème de la tangente et le calcul différentiel

Le taux de variation est l'un des concepts les plus critiques du calcul. Nous commençons notre étude des taux de variation en examinant les graphiques des trois lignes et\(f(x)=−2x−3,\; g(x)=\dfrac{1}{2}x+1\)\(h(x)=2\), comme le montre la figure\(\PageIndex{1}\).

Trois graphiques en ligne droite. L'un, intitulé « f (x) = -2x - 3 », diminue en croisant l'axe x à -1,5 et l'axe y à -3 ; un autre, étiqueté « g (x) = x/2 + 1 », augmente en croisant l'axe x en -2 et l'axe y en 1 ; le troisième, étiqueté « h (x) = 2 », est plat à la coordonnée y 2 — Figure\(\PageIndex{1}\) : Le taux de variation d'une fonction linéaire est constant dans chacun de ces trois graphes, la constante étant déterminée par la pente.

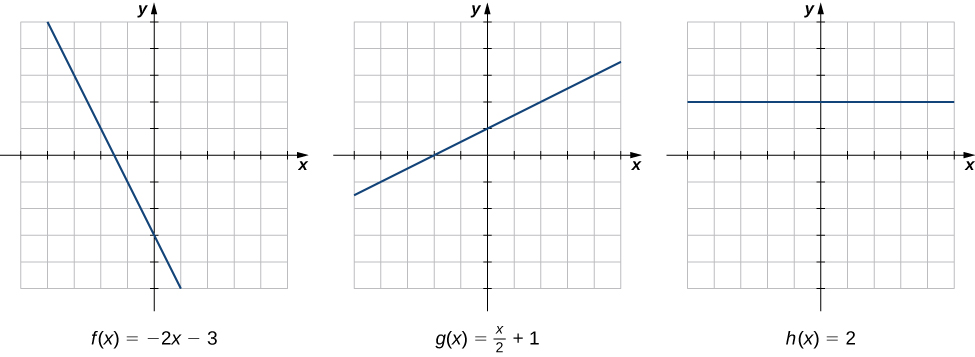
Lorsque nous nous déplaçons de gauche à droite le long du graphique de\(f(x)=−2x−3\), nous constatons que le graphique diminue à un rythme constant. Pour chaque\(1\) unité que nous déplaçons vers la droite le long de\(x\) l'axe -, la\(y\) coordonnée -diminue d'une\(2\) unité. Ce taux de variation est déterminé par la pente (\(−2\)) de la ligne. De même, la pente de\(1/2\) dans la fonction nous\(g(x)\) indique que pour chaque changement\(x\) d'\(1\)unité, il y a un changement\(y\) d'\(1/2\)unité correspondant. La fonction\(h(x)=2\) a une pente nulle, ce qui indique que les valeurs de la fonction restent constantes. Nous voyons que la pente de chaque fonction linéaire indique le taux de variation de la fonction.

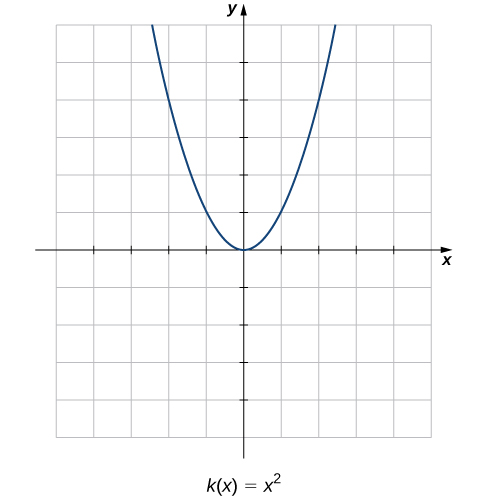
Comparez les graphes de ces trois fonctions avec le graphique de\(k(x)=x^2\) (Figure\(\PageIndex{2}\)). Le graphique\(k(x)=x^2\) commence à partir de la gauche en diminuant rapidement, puis commence à diminuer plus lentement et à se stabiliser, puis commence enfin à augmenter, lentement au début, suivi d'un taux d'augmentation croissant à mesure qu'il se déplace vers la droite. Contrairement à une fonction linéaire, aucun nombre ne représente le taux de variation de cette fonction. Nous nous posons naturellement la question suivante : comment mesurer le taux de variation d'une fonction non linéaire ?

Un graphe de la parabole k (x) = x^2, qui s'ouvre et dont le sommet est à l'origine. — Figure\(\PageIndex{2}\) : La fonction\(k(x)=x^2\) n'a pas de taux de variation constant.

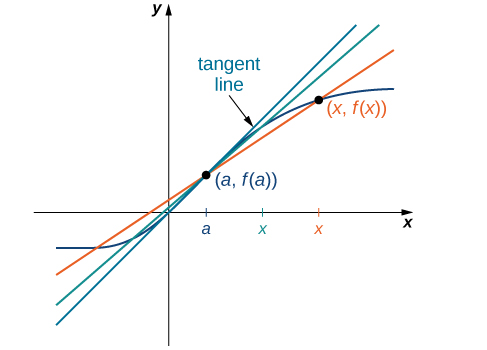
Nous pouvons estimer le taux de variation d'une fonction\(f(x)\) à un point\((a,f(a))\) de son graphique en prenant un autre point\((x,f(x))\) sur le graphique de\(f(x)\), en traçant une ligne passant par les deux points et en calculant la pente de la droite résultante. Une telle ligne est appelée ligne sécante. La figure\(\PageIndex{3}\) montre une ligne sécante menant à une fonction\(f(x)\) en un point\((a,f(a))\).

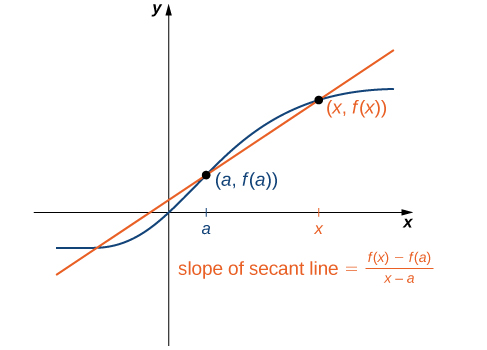
Un graphique montrant une fonction courbe générique passant par les points (0,0), (a, fa.) et (x, f (x)). Une ligne droite appelée ligne sécante est tracée entre les points (a, fa.) et (x, f (x)), passant en dessous de la fonction courbe entre a et x et au-dessus de la fonction courbe à des valeurs supérieures à x ou inférieures à a. La fonction courbe et la droite sécante se croisent à nouveau à un moment donné du troisième quadrant. La pente de la droite sécante est (f (x) — fa.)/(x — a). — Figure\(\PageIndex{3}\) : La pente d'une droite sécante passant par un point permet d'\((a,f(a))\)estimer le taux de variation de la fonction au point\((a,f(a))\).

Nous définissons formellement une ligne sécante comme suit :

Définition : Secant Line

La sécante de la fonction\(f(x)\) passant par les points\((a,f(a))\) et\((x,f(x))\) est la droite passant par ces points. Sa pente est donnée par

\[m_{sec}=\dfrac{f(x)−f(a)}{x−a}. \label{secantslope} \]

La précision de l'approximation du taux de variation de la fonction à l'aide d'une droite sécante dépend de la proximité\(x\) de\(a\). Comme nous le voyons sur la figure\(\PageIndex{4}\), si elle\(x\) est plus proche de\(a\), la pente de la droite sécante est une meilleure mesure du taux de variation de\(f(x)\) at\(a\).

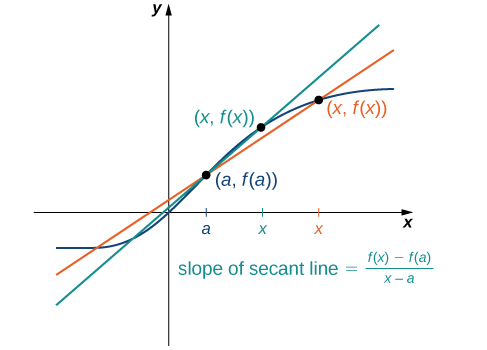
Ce graphique est identique à la ligne sécante précédente et au graphe à fonctions courbes générique. Cependant, un autre point x est ajouté, cette fois tracé plus proche de a sur l'axe des abscisses. Ainsi, une autre ligne sécante est tracée entre les points (a, fa.) et la nouvelle, plus proche (x, f (x)). La ligne reste beaucoup plus proche de la fonction courbe générique autour de (a, fa.). La pente de cette droite sécante est devenue une meilleure approximation du taux de variation de la fonction générique. — Figure\(\PageIndex{4}\) : À mesure que l'on s'en\(x\) rapproche\(a\), la pente de la droite sécante devient une meilleure approximation du taux de variation de la fonction\(f(x)\) à\(a\).

Les droites sécantes elles-mêmes s'approchent d'une droite appelée tangente à la fonction\(f(x)\) at\(a\) (Figure\(\PageIndex{5}\)). La pente de la tangente au graphique à\(a\) mesure le taux de variation de la fonction à\(a\). Cette valeur représente également la dérivée de la fonction\(f(x)\) at\(a\), ou le taux de variation de la fonction at\(a\). Ce dérivé est désigné par\(f′(a)\). Le calcul différentiel est le domaine du calcul qui concerne l'étude des dérivés et de leurs applications.

Ce graphique s'inscrit dans la continuité des deux précédents. Cette fois, le graphique contient la fonction courbe, les deux droites sécantes et une tangente. Lorsque x s'approche de a, les droites sécantes s'approchent de la tangente. — Figure\(\PageIndex{5}\) : Résolution du problème de la tangente : À mesure que l'on\(x\) s'approche\(a\), les droites sécantes s'approchent de la tangente.

Un exemple\(\PageIndex{1}\) montre comment déterminer les pentes des lignes sécantes. Ces pentes estiment la pente de la tangente ou, de manière équivalente, le taux de variation de la fonction au point où les pentes sont calculées.

Exemple\(\PageIndex{1}\): Finding Slopes of Secant Lines

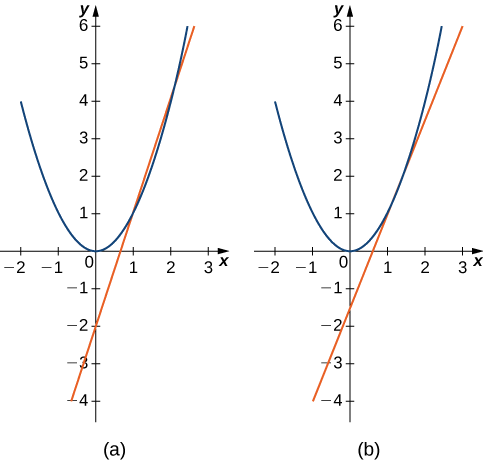
Estimez la pente de la tangente (taux de variation)\(x=1\) par rapport à\(f(x)=x^2\) at en trouvant les pentes des droites sécantes passant par\((1,1)\) et chacun des points suivants sur le graphique de\(f(x)=x^2\).

\((2,4)\)
\(\left(\dfrac{3}{2},\dfrac{9}{4}\right)\)

Solution :

Utilisez la formule pour la pente d'une droite sécante (équation \ ref {secantslope}).

\(m_{sec}=\dfrac{4−1}{2−1}=3\)
\(m_{sec}=\dfrac{\dfrac{9}{4}−1}{\dfrac{3}{2}−1}=\dfrac{5}{2}=2.5\)

Le point de la partie b. est plus proche du point\((1,1)\), de sorte que la pente de\(2.5\) est plus proche de la pente de la tangente. Une bonne estimation de la pente de la tangente serait comprise entre et\(2.5\) (Figure\(\PageIndex{6}\)).\(2\)

Deux graphes de la parabole f (x) = x^2 sont présentés. La première comporte une ligne sécante qui coupe la parabole en (1,1) et (2,4). La seconde est tracée par une ligne sécante qui coupe la parabole en (1,1) et (3/2, 9/4). Ces droites fournissent des approximations successives plus proches de la tangente à la fonction at (1,1). — Figure\(\PageIndex{6}\) : Les droites sécantes\(f(x)=x^2\) allant\((1,1)\) de at à (a)\((2,4)\) et (b)\((\dfrac{3}{2},\dfrac{9}{4})\) fournissent des approximations successives plus proches de la droite tangente à\(f(x)=x^2\) at\((1,1)\).

Exercice\(\PageIndex{1}\)

Estimez la pente de la tangente (taux de variation)\(x=1\) par rapport à\(f(x)=x^2\) at en trouvant les pentes des droites sécantes\((1,1)\) traversantes et le point\((\dfrac{5}{4},\dfrac{25}{16})\) sur le graphique de\(f(x)=x^2\).

Réponse: \(2.25\)

Nous poursuivons notre enquête en explorant une question connexe. En gardant à l'esprit que la vitesse peut être considérée comme le taux de changement de position, supposons que nous ayons une fonction qui donne la position d'un objet le long d'un axe de coordonnées à un moment donné\(t\).\(s(t)\) Pouvons-nous utiliser ces mêmes idées pour créer une définition raisonnable de la vitesse instantanée à un moment donné\(t=a?\) ? Nous commençons par approximer la vitesse instantanée avec une vitesse moyenne. Tout d'abord, rappelons que la vitesse d'un objet se déplaçant à une vitesse constante est le rapport entre la distance parcourue et le temps qu'il a parcouru. Nous définissons la vitesse moyenne d'un objet sur une période comme étant le changement de sa position divisé par la durée de la période.

Définition : vitesse moyenne

\(s(t)\)Soit la position d'un objet se déplaçant le long d'un axe de coordonnées à la fois\(t\). La vitesse moyenne de l'objet sur un intervalle de temps\([a,t]\) où\(a<t\) (ou\([t,a]\) si)\(t<a)\) est

\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \label{avgvel} \]

Au fur\(t\) et à mesure que l'on choisit de plus près\(a\), la vitesse moyenne se rapproche de la vitesse instantanée. Notez que la détermination de la vitesse moyenne d'une fonction de position sur un intervalle de temps revient essentiellement à déterminer la pente d'une droite sécante par rapport à une fonction. De plus, pour déterminer la pente d'une tangente en un point\(a\), nous laissons les\(x\) valeurs -s' approcher\(a\) de la pente de la droite sécante. De même, pour trouver la vitesse instantanée dans le temps\(a\), nous laissons les\(t\) valeurs -s' approcher\(a\) de la vitesse moyenne. Ce processus qui consiste à laisser\(x\) ou\(a\) à\(t\) aborder une expression s'appelle prendre une limite. Ainsi, nous pouvons définir la vitesse instantanée comme suit.

Définition : vitesse instantanée

Pour une fonction de position\(s(t)\), la vitesse instantanée à un moment donné\(t=a\) est la valeur à laquelle les vitesses moyennes se rapprochent à des intervalles de la forme\([a,t]\) et à\([t,a]\) mesure que les valeurs de ces valeurs\(t\) se rapprochent\(a\), à condition qu'une telle valeur existe.

L'exemple\(\PageIndex{2}\) illustre ce concept de limites et de vitesse moyenne.

Exemple\(\PageIndex{2}\): Finding Average Velocity

Un rocher tombe d'une hauteur de 64 pieds. Il est déterminé que sa hauteur (en pieds) au-dessus du sol t secondes plus tard (pour\(0≤t≤2\)) est donnée par\(s(t)=−16t^2+64\). Détermine la vitesse moyenne de la roche sur chacun des intervalles de temps donnés. Utilisez ces informations pour deviner la vitesse instantanée de la roche à un moment donné\(t=0.5\).

[\(0.49,0.5\)]
[\(0.5,0.51\)]

Solution

Substituez les données dans l'équation \ ref {avgvel} pour la définition de la vitesse moyenne.

\[v_{ave}=\dfrac{s(0.49)−s(0.5)}{0.49−0.5}=−15.84 \nonumber \]
\[v_{ave}=\dfrac{s(0.51)−s(0.5)}{0.51−0.5}=−16.016 \nonumber \]

La vitesse instantanée se situe entre −15,84 et −16,16 pieds/sec. Une bonne estimation pourrait être de −16 pieds/sec.

Exercice\(\PageIndex{2}\)

Un objet se déplace le long d'un axe de coordonnées de telle sorte que sa position temporelle\(t\) soit donnée par\(s(t)=t^3\). Estimez sa vitesse instantanée dans le temps\(t=2\) en calculant sa vitesse moyenne sur l'intervalle de temps [\(2,2.001\)].

Allusion: Utilisez l'équation \ ref {avgvel} avec\(v_{ave}=\dfrac{s(2.001)−s(2)}{2.001−2}\).

Réponse: 12.006001

Le problème de la zone et le calcul intégral

Nous tournons maintenant notre attention vers une question classique issue du calcul. De nombreuses grandeurs physiques, par exemple des quantités de travail, peuvent être interprétées comme la surface sous une courbe. Cela nous amène à nous poser la question suivante : Comment trouver l'aire entre le graphe d'une fonction et l'\(x\)axe -sur un intervalle (Figure\(\PageIndex{7}\)) ?

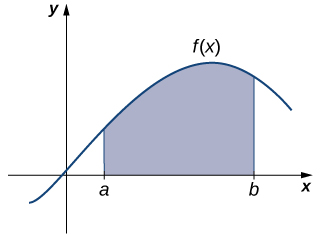
Un graphique montre une fonction courbe générique f (x) ayant la forme d'une colline dans le premier quadrant. Une zone située sous la fonction est ombrée au-dessus de l'axe X et entre x=a et x=b. — Figure\(\PageIndex{7}\) : Le problème de la zone : comment trouver la zone de la zone ombrée ?

Comme dans la réponse à nos questions précédentes sur la vélocité, nous essayons d'abord d'approximer la solution. Nous approximons la surface en divisant l'intervalle\([a,b]\) en intervalles plus petits sous forme de rectangles. L'approximation de l'aire provient de l'addition des aires de ces rectangles (Figure\(\PageIndex{8}\)).

Le graphique est identique à l'image précédente, à une différence près. Au lieu de la zone complètement ombrée sous la fonction incurvée, l'intervalle [a, b] est divisé en intervalles plus petits sous la forme de rectangles. Les rectangles ont la même faible largeur. La hauteur de chaque rectangle est la hauteur de la fonction au milieu de la base de ce rectangle spécifique. — Figure\(\PageIndex{8}\) : L'aire de la région située sous la courbe est approximée en additionnant les aires des rectangles fins.

À mesure que les largeurs des rectangles diminuent (approche de zéro), les sommes des aires des rectangles se rapprochent de la zone située entre le graphique de\(f(x)\) et l'\(x\)axe y sur l'intervalle\([a,b]\). Une fois de plus, nous nous retrouvons face à une limite. Les limites de ce type servent de base à la définition de l'intégrale définie. Le calcul intégral est l'étude des intégrales et de leurs applications.

Exemple\(\PageIndex{3}\): Estimation Using Rectangles

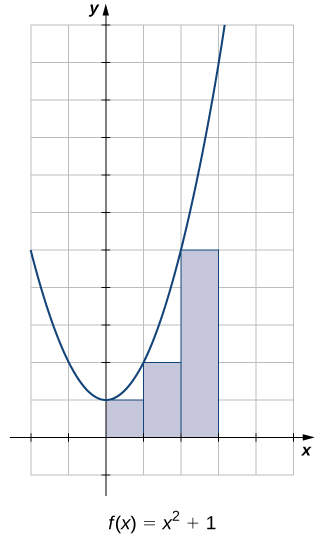
Estimez l'aire entre l'\(x\)axe -et le graphe de\(f(x)=x^2+1\) sur l'intervalle en\([0,3]\) utilisant les trois rectangles illustrés sur la figure\(\PageIndex{9}\).

Graphique d'une parabole s'ouvrant vers le haut avec le point le plus bas à (0,1). Un rectangle de hauteur 1 s'étendant de x=0 à x=1 touche la parabole au point (0,1) ; un rectangle de hauteur 2 de x=1 à x=2 la touche au point (1,2) ; un rectangle de hauteur 5 de x=2 à x=3 la touche au point (2,5) — Figure\(\PageIndex{9}\) : L'aire de la région située sous la courbe de\(f(x)=x^2+1\) peut être estimée à l'aide de rectangles.

Solution

Les surfaces des trois rectangles sont de 1 unité ², 2 unités ² et 5 unités ². En utilisant ces rectangles, notre estimation de superficie est de 8 unités ².

Exercice\(\PageIndex{3}\)

Estimez l'aire entre l'\(x\)axe -et le graphe de\(f(x)=x^2+1\) sur l'intervalle en\([0,3]\) utilisant les trois rectangles illustrés sur la figure\(\PageIndex{10}\).

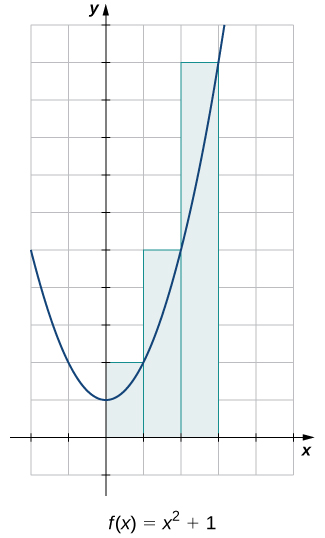
Graphique d'une parabole s'ouvrant vers le haut, avec son point le plus bas au point (0,1). Un rectangle de hauteur 2 et s'étendant de x=0 à x=1 touche la parabole au point (1,2) ; un rectangle de hauteur 5 de x=1 à x=2 la touche au point (2,5) ; un rectangle de hauteur 10 de x=2 à x=3 la touche au point (3,10) — Figure\(\PageIndex{10}\) : L'aire de la région située sous la courbe de\(f(x)=x^2+1\) peut être estimée à l'aide de rectangles.

Allusion: Utilisez l'exemple\(\PageIndex{3}\) comme guide

Réponse: 17\(\mathrm{unit}^2\)

Autres aspects du calcul

Jusqu'à présent, nous avons étudié les fonctions d'une seule variable. Ces fonctions peuvent être représentées visuellement à l'aide de graphiques en deux dimensions ; toutefois, il n'y a aucune raison valable de limiter notre étude à deux dimensions. Supposons, par exemple, qu'au lieu de déterminer la vitesse d'un objet se déplaçant le long d'un axe de coordonnées, nous souhaitions déterminer la vitesse d'un rocher tiré d'une catapulte à un moment donné, ou celle d'un avion se déplaçant en trois dimensions. Nous pouvons vouloir représenter graphiquement les fonctions en valeur réelle de deux variables ou déterminer des volumes de solides du type illustré à la figure\(\PageIndex{11}\). Ce ne sont là que quelques-uns des types de questions qui peuvent être posées et auxquelles il est possible de répondre à l'aide du calcul multivariable. De manière informelle, le calcul multivariable peut être caractérisé comme l'étude du calcul des fonctions de deux variables ou plus. Cependant, avant d'explorer ces idées et d'autres, nous devons d'abord jeter les bases de l'étude du calcul dans une variable en explorant le concept de limite.

Un diagramme dans un espace tridimensionnel, sur les axes x, y et z où z = f (x, y). La base est l'axe x, y et la hauteur est l'axe z. La base est un rectangle contenu dans le plan de l'axe x, y. Le sommet est une surface de hauteur variable avec des coins situés directement au-dessus de ceux du rectangle dans le plan x, y.. Le point le plus haut se trouve au-dessus du coin à x=0, y=0. Le point le plus bas se trouve à l'angle situé quelque part dans le premier quadrant du plan x, y. Les deux autres points ont à peu près la même hauteur et sont situés au-dessus des coins des axes x et y. Des lignes sont tracées pour relier les coins du rectangle à ceux de la surface. — Figure\(\PageIndex{11}\) : Nous pouvons utiliser le calcul multivariable pour déterminer le volume entre une surface définie par une fonction de deux variables et un plan.

Concepts clés

Le calcul différentiel est né de la tentative de résoudre le problème de la détermination de la pente d'une droite tangente à une courbe en un point. La pente de la tangente indique le taux de variation de la fonction, également appelé dérivée. Pour calculer une dérivée, il faut trouver une limite.
Le calcul intégral est né de la tentative de résoudre le problème de la détermination de l'aire d'une région située entre le graphe d'une fonction et l'\(x\)axe. Nous pouvons approximer la surface en la divisant en rectangles fins et en additionnant les surfaces de ces rectangles. Cette sommation conduit à la valeur d'une fonction appelée intégrale. L'intégrale est également calculée en déterminant une limite et, en fait, est liée à la dérivée d'une fonction.
Le calcul multivariable nous permet de résoudre des problèmes dans l'espace tridimensionnel, notamment de déterminer le mouvement dans l'espace et de trouver des volumes de solides.

Équations clés

Pente d'une ligne sécante

\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

Vitesse moyenne sur l'intervalle [a, t]

\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

Lexique

vitesse moyenne: le changement de position d'un objet divisé par la durée d'une période ; la vitesse moyenne d'un objet sur un intervalle de temps [\(t,a\)] (si\(t<a\) ou [\(a,t\)] si\(t>a\)), avec une position donnée par\(s(t)\), c'est-à-dire\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

calcul différentiel: le domaine du calcul qui concerne l'étude des dérivés et de leurs applications

vitesse instantanée: La vitesse instantanée d'un objet dont la fonction de position est donnée par\(s(t)\) est la valeur à laquelle les vitesses moyennes sur les intervalles de la forme [\(t,a\)] et [\(a,t\)] se rapprochent lorsque les valeurs de\(t\) se rapprochent\(a\), à condition qu'une telle valeur existe

calcul intégral: l'étude des intégrales et de leurs applications

limite: le processus qui consiste à laisser x ou t s'approcher de a dans une expression ; la limite d'une fonction\(f(x)\) en tant qu'\(x\)approches\(a\) est la valeur qui s'\(f(x)\)approche en tant qu'\(x\)approches\(a\)

calcul multivariable: l'étude du calcul des fonctions de deux variables ou plus

sécant: Une droite sécante menant à une fonction\(f(x)\) at\(a\) est une droite passant par le point (\(a,f(a)\)) et un autre point de la fonction ; la pente de la droite sécante est donnée par\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

tangente: Une tangente au graphe d'une fonction en un point (\(a,f(a)\)) est la droite que les lignes sécantes traversent (\(a,f(a)\)) lorsqu'elles passent par des points de la fonction dont\(x\) les valeurs se rapprochent\(a\) ; la pente de la tangente à un graphique\(a\) mesure le taux de variation de la fonction à\(a\)