1.5E : Exercices pour la section 1.5

Last updated
Save as PDF

Page ID: 197957

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 4, évaluez les fonctions exponentielles données comme indiqué, avec une précision de deux chiffres significatifs après la décimale.

1)$f(x)=5^x$

un.$x=3$

b.$x=\frac{1}{2}$

c.$x=\sqrt{2}$

Réponse: a.$125$
b.$2.24$
c.$9.74$

2)$f(x)=(0.3)^x$

un.$x=−1$

b.$x=4$

c.$x=−1.5$

3)$f(x)=10^x$

un.$x=−2$

b.$x=4$

c.$x=\frac{5}{3}$

Réponse: a.$0.01$
b.$10,000$
c.$46.42$

4)$f(x)=e^x$

un.$x=2$

b.$x=−3.2$

c.$x=π$

Dans les exercices 5 à 10, associez l'équation exponentielle au graphique correct.

un.$y=4^{−x}$

b.$y=3^{x−1}$

c.$y=2^{x+1}$

d.$y=\left(\frac{1}{2}\right)^x+2$

e.$y=−3^{−x}$

f).$y=1−5^x$

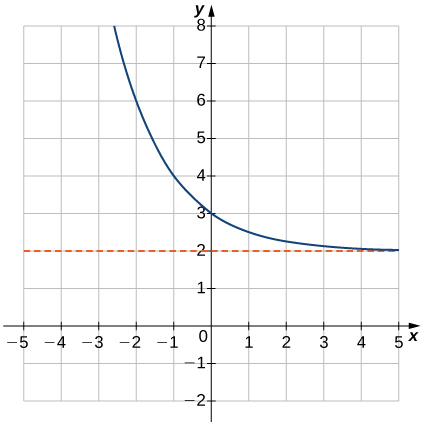
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y de -2 à 8. Le graphique présente une fonction courbe décroissante. La fonction diminue jusqu'à ce qu'elle s'approche de la ligne « y = 2 », mais ne touche jamais cette ligne. L'intersection y se trouve au point (0, 3) et il n'y a pas d'intersection X.$

Réponse: d

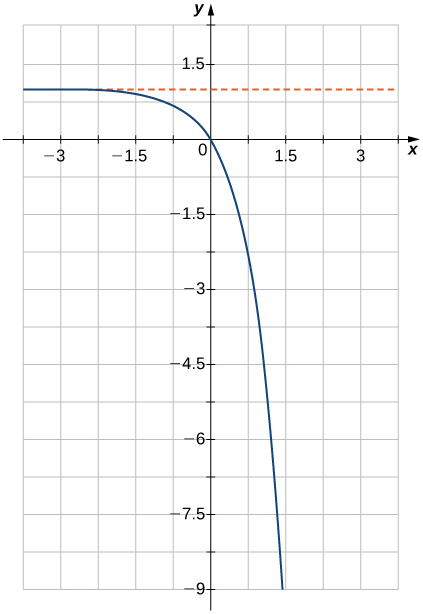
$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -9 à 2. Le graphique représente une fonction qui commence légèrement en dessous de la ligne « y = 1 » et qui commence à décroître rapidement dans une courbe. L'intersection x et l'intersection y sont toutes deux à l'origine.$

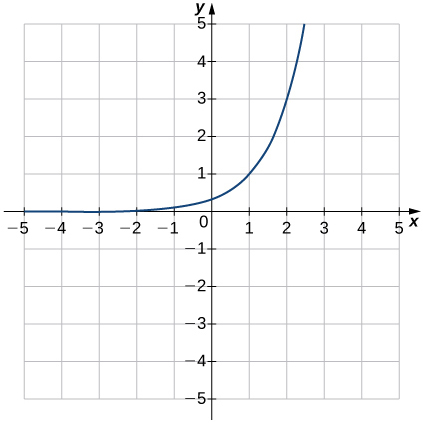
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une fonction croissante incurvée qui commence légèrement au-dessus de l'axe x et commence à augmenter rapidement. Il n'y a pas d'intersection X et l'intersection y se trouve au point (0, (1/3)). Un autre point du graphique se trouve à (1, 1).$

Réponse: b

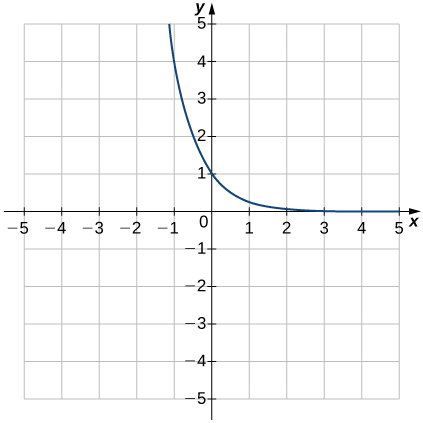
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique présente une fonction décroissante incurvée qui diminue jusqu'à ce qu'il se rapproche de l'axe x sans le toucher. Il n'y a pas d'intersection X et l'intersection y se trouve au point (0, 1). Un autre point du graphique se trouve à (-1, 4).$

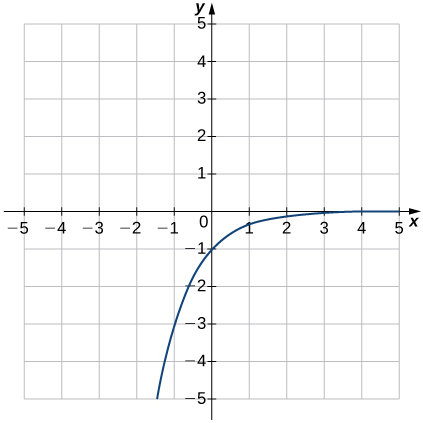
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique présente une fonction d'augmentation incurvée qui augmente jusqu'à ce qu'il se rapproche de l'axe x sans le toucher. Il n'y a pas d'intersection x et l'intersection y se trouve au point (0, -1). Un autre point du graphique se trouve à (-1, -3).$

Réponse: e

10)

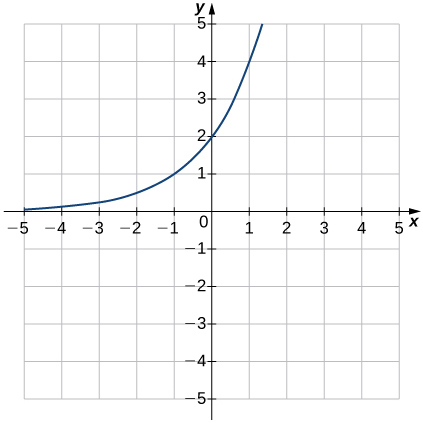
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une fonction croissante incurvée qui commence légèrement au-dessus de l'axe x et commence à augmenter rapidement. Il n'y a pas d'intersection X et l'intersection y se trouve au point (0, 2). Un autre point du graphique se trouve à (-1, 1).$

Dans les exercices 11 à 17, esquissez le graphique de la fonction exponentielle. Déterminez le domaine, la plage et l'asymptote horizontale.

11)$f(x)=e^x+2$

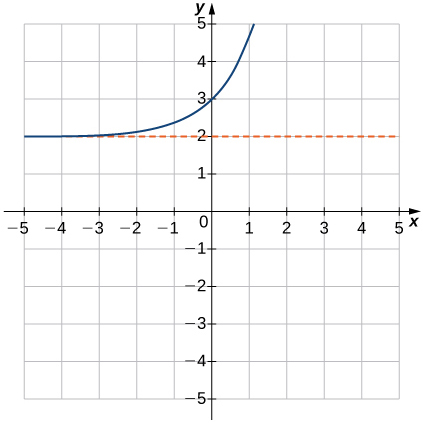
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une fonction croissante incurvée qui commence légèrement au-dessus de la ligne « y = 2 » et commence à augmenter rapidement. Il n'y a pas d'intersection x et l'intersection y se trouve au point (0, 3).$

Réponse: Domaine : tous les nombres réels, plage :$(2,∞),\; y=2$

(12)$f(x)=−2^x$

$alt$

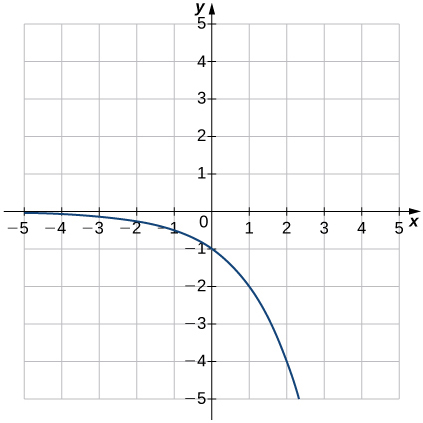
(13)$f(x)=3^{x+1}$

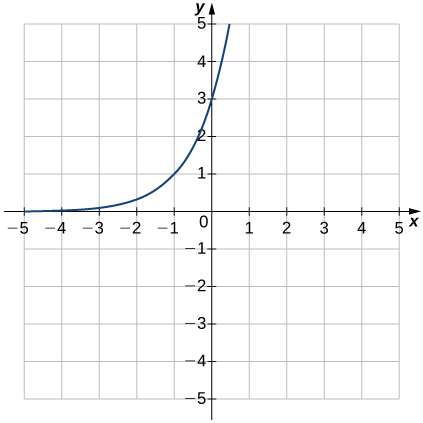
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une fonction croissante incurvée qui commence légèrement au-dessus de l'axe x et commence à augmenter rapidement. Il n'y a pas d'intersection x et l'intersection y se trouve au point (0, 3). Un autre point du graphique se trouve à (-1, 1).$

Réponse: Domaine : tous les nombres réels, plage :$(0,∞),\; y=0$

(14)$f(x)=4^x−1$

$alt$

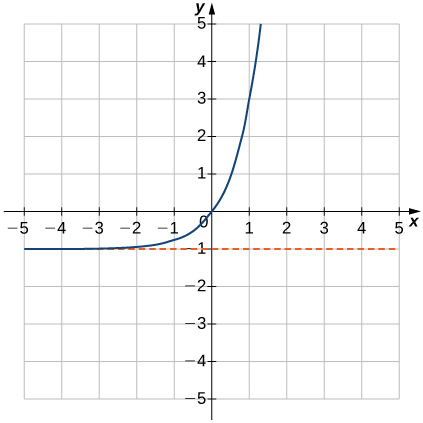
(15)$f(x)=1−2^{−x}$

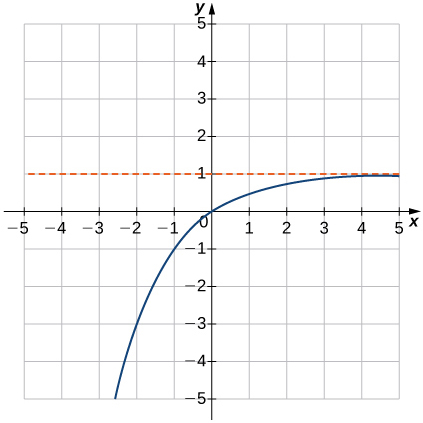
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique présente une fonction croissante incurvée qui augmente jusqu'à ce qu'il se rapproche de la ligne « y = 1 » sans la toucher. L'intersection x et l'intersection y sont toutes deux à l'origine. Un autre point du graphique se trouve à (-1, -1).$

Réponse: Domaine : tous les nombres réels, plage :$(−∞,1),\; y=1$

16)$f(x)=5^{x+1}+2$

$alt$

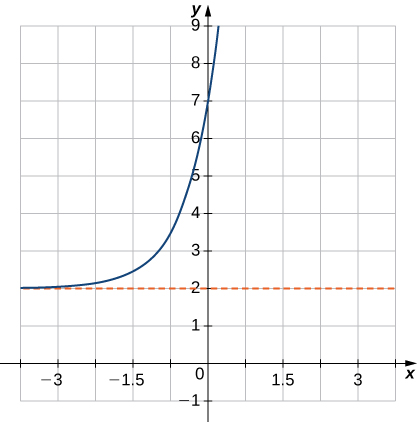
17)$f(x)=e^{−x}−1$

$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique présente une fonction décroissante incurvée qui diminue jusqu'à ce qu'elle se rapproche de la ligne « y = -1 » sans la toucher. L'intersection x et l'intersection y sont toutes deux à l'origine. Il y a un point approximatif sur le graphique à (-1, 1,7).$

Réponse: Domaine : tous les nombres réels, plage :$(−1,∞), \;y=−1$

Dans les exercices 18 à 25, écrivez l'équation sous forme exponentielle équivalente.

18)$\log_3 81=4$

19)$\log_8 2=\frac{1}{3}$

Réponse: $8^{1/3}=2$

(20)$\log_5 1=0$

(21)$\log_5 25=2$

Réponse: $5^2=25$

(22)$\log 0.1=−1$

23)$\ln\left(\frac{1}{e^3}\right)=−3$

Réponse: $e^{−3}=\dfrac{1}{e^3}$

(24)$\log_9 3=0.5$

25)$\ln 1=0$

Réponse: $e^0=1$

Dans les exercices 26 à 35, écrivez l'équation sous une forme logarithmique équivalente.

(26)$2^3=8$

(27)$4^{−2}=\frac{1}{16}$

Réponse: $\log_4\left(\frac{1}{16}\right)=−2$

(28)$10^2=100$

(29)$9^0=1$

Réponse: $\log_9 1=0$

(30)$\left(\frac{1}{3}\right)^3=\frac{1}{27}$

31)$\sqrt[3]{64}=4$

Réponse: $\log_{64}4=\frac{1}{3}$

32)$e^x=y$

33)$9^y=150$

Réponse: $\log_9 150=y$

34)$b^3=45$

35)$4^{-3/2}=0.125$

Réponse: $\log_4 0.125=−\frac{3}{2}$

Dans les exercices 36 à 41, esquissez le graphique de la fonction logarithmique. Déterminez le domaine, la plage et l'asymptote verticale.

36)$f(x)=3+\ln x$

$alt$

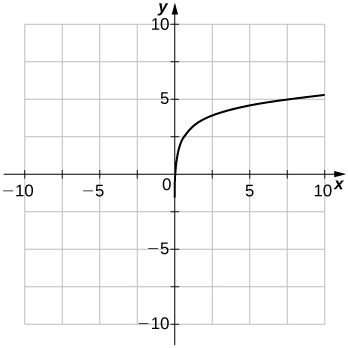
(37)$f(x)=\ln(x−1)$

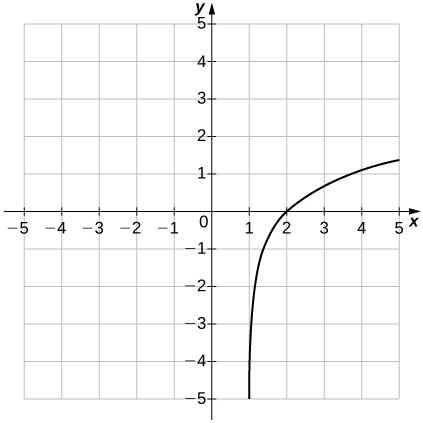
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une fonction courbe croissante qui commence légèrement à droite de la ligne verticale « x = 1 ». Il n'y a pas d'intersection y et l'intersection x se trouve au point approximatif (2, 0).$

Réponse: Domaine :$(1,∞)$, Gamme :$(−∞,∞),\; x=1$

38)$f(x)=\ln(−x)$

$alt$

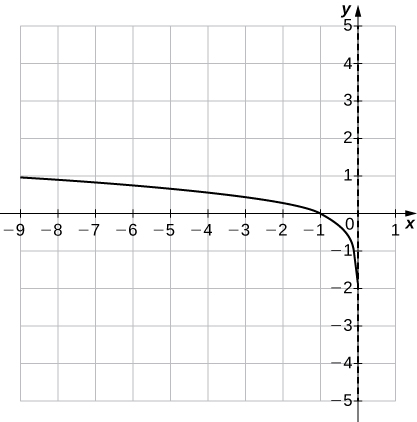
39)$f(x)=1−\ln x$

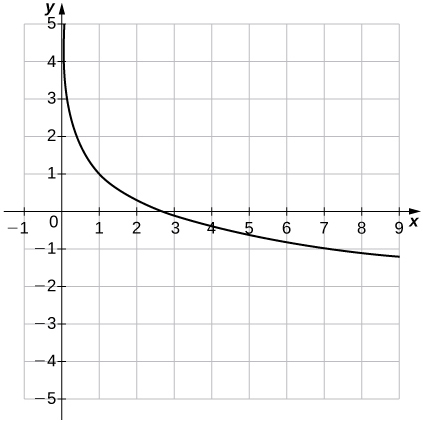
$Image d'un graphique. L'axe x va de -1 à 9 et l'axe y va de -5 à 5. Le graphique représente une fonction courbe décroissante qui commence légèrement à droite de l'axe y. Il n'y a pas d'intersection y et l'intersection x se trouve au point (e, 0).$

Réponse: Domaine :$(0,∞)$, Gamme :$(−∞,∞),\; x=0$

40)$f(x)=\log x−1$

$221$

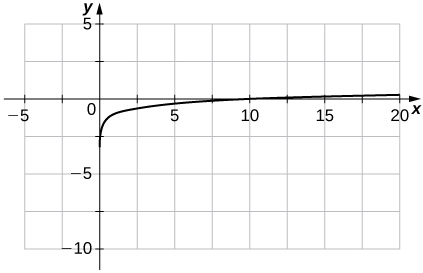
41)$f(x)=\ln(x+1)$

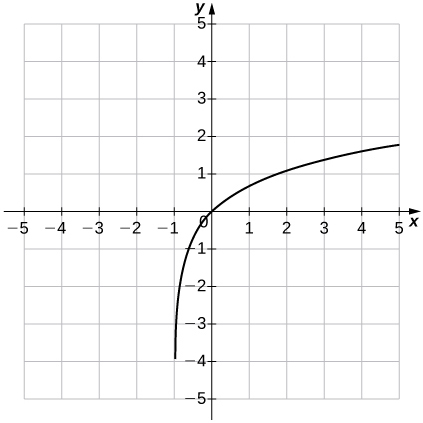
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une fonction courbe croissante qui commence légèrement à droite de la ligne verticale « x = -1 ». L'intersection y et l'intersection x sont toutes deux à l'origine.$

Réponse: Domaine :$(−1,∞)$, Gamme :$(−∞,∞)$,$x=−1$

Dans les exercices 42 à 47, utilisez les propriétés des logarithmes pour écrire les expressions sous forme de somme, de différence et/ou de produit de logarithmes.

(42)$\log x^4y$

43)$\log_3\frac{9a^3}{b}$

Réponse: $2+3\log_3 a−\log_3 b$

44)$\ln a\sqrt[3]{b}$

45)$\log_5\sqrt{125xy^3}$

Réponse: $\frac{3}{2}+\frac{1}{2}\log_5 x+\frac{3}{2}\log_5 y$

46)$\log_4 \frac{\sqrt[3]{xy}}{64}$

47)$\ln\left(\frac{6}{\sqrt{e^3}}\right)$

Réponse: $−\frac{3}{2}+\ln 6$

Dans les exercices 48 à 55, résolvez exactement l'équation exponentielle.

48)$5^x=125$

49)$e^{3x}−15=0$

Réponse: $\frac{\ln 15}{3}$

50)$8^x=4$

51)$4^{x+1}−32=0$

Réponse: $\frac{3}{2}$

52)$3^{x/14}=\frac{1}{10}$

53)$10^x=7.21$

Réponse: $\log 7.21$

(54)$4⋅2^{3x}−20=0$

55)$7^{3x−2}=11$

Réponse: $\frac{2}{3}+\frac{\log 11}{3\log 7}$

Dans les exercices 56 à 63, résolvez exactement l'équation logarithmique, si possible.

56)$\log_3 x=0$

(57)$\log_5 x=−2$

Réponse: $x=\frac{1}{25}$

58)$\log_4(x+5)=0$

59)$\log(2x−7)=0$

Réponse: $x=4$

(60)$\ln\sqrt{x+3}=2$

61)$\log_6(x+9)+\log_6 x=2$

Réponse: $x=3$

62)$\log_4(x+2)−\log_4(x−1)=0$

63)$\ln x+\ln(x−2)=\ln 4$

Réponse: $1+\sqrt{5}$

Dans les exercices 64 à 69, utilisez la formule de changement de base et la base$10$ ou la base$e$ pour évaluer les expressions données. Répondez sous une forme exacte et approximative, en arrondissant à quatre décimales.

64)$\log_5 47$

(65)$\log_7 82$

Réponse: $\dfrac{\log 82}{\log 7}≈2.2646$

66)$\log_6 103$

67)$\log_{0.5}211$

Réponse: $\dfrac{\log 211}{\log 0.5}≈−7.7211$

68)$\log_2 π$

69)$\log_{0.2}0.452$

Réponse: $\dfrac{\log 0.452}{\log 0.2}≈0.4934$

70) Réécrivez les expressions suivantes en termes d'exponentielles et simplifiez-les.

a.$2\cosh(\ln x)$ b.$\cosh 4x+\sinh 4x$ c.$\cosh 2x−\sinh 2x$ d.$\ln(\cosh x+\sinh x)+\ln(\cosh x−\sinh x)$

71) [T] Le nombre de bactéries présentes$N$ dans une culture après plusieurs$t$ jours peut être modélisé par la fonction$N(t)=1300⋅(2)^{t/4}$. Déterminez le nombre de bactéries présentes après plusieurs$15$ jours.

Réponse: $\sim 17,491$

72) [T] La demande$D$ (en millions de barils) de pétrole dans un pays riche en pétrole est donnée par la fonction$D(p)=150⋅(2.7)^{−0.25p}$, où$p$ est le prix (en dollars) du baril de pétrole. Déterminez la quantité de pétrole demandée (au million de barils près) lorsque le prix se situe entre 15 et 20 dollars.

73) [T] Le montant$A$ d'un investissement de 100 000$ payé de façon continue et composé pendant t années est donné par$A(t)=100,000⋅e^{0.055t}$. Déterminez le montant$A$ accumulé en$5$ années.

Réponse: Environ 131 653$ sont accumulés en 5 ans.

74) [T] Un investissement est composé mensuellement, trimestriellement ou annuellement et est donné par la fonction$A=P\left(1+\frac{j}{n}\right)^{nt}$, où$A$ est la valeur de l'investissement à un moment donné$t$,$P$ est le principe initial qui a été investi,$j$ est le taux d'intérêt annuel et$n$ est le nombre de fois les intérêts sont composés chaque année. Sur la base d'un taux d'intérêt annuel de 3,5 % et d'un principe initial de 100 000$, déterminez le montant$A$ accumulé en 5 ans pour les intérêts composés a. quotidiens, b. mensuels, c. trimestriels et d. annuels.

75) [T] La concentration en ions hydrogène dans une substance est désignée par$[H+]$, mesurée en moles par litre. Le pH d'une substance est défini par la fonction logarithmique$pH=−\log[H+]$. Cette fonction permet de mesurer l'acidité d'une substance. Le pH de l'eau est de 7. Une substance dont le pH est inférieur à 7 est un acide, tandis qu'une substance dont le pH est supérieur à 7 est une base.

a. Déterminez le pH des substances suivantes. Arrondissez les réponses à un chiffre.

b. Déterminez si la substance est un acide ou une base.

i. Œufs :$[H+]=1.6×10^{−8}$ mol/L

ii. Bière :$[H+]=3.16×10^{−3}$ mol/L

iii. Jus de tomate :$[H+]=7.94×10^{−5}$ mol/L

Réponse: i. a. pH = 8 b. Base
ii. a. pH = 3 b. Acide
iii. a. pH = 4 b. Acide

76) [T] L'iode 131 est une substance radioactive qui se désintègre en fonction de la fonction$Q(t)=Q_0⋅e^{−0.08664t}$, où$Q_0$ est la quantité initiale d'un échantillon de la substance$t$ exprimée en jours. Déterminez le temps qu'il faut (au jour le plus proche) pour que 95 % d'une quantité se décompose.

77) [T] Selon la Banque mondiale, fin 2013$(t=0)$, la population américaine était de 316 millions d'habitants et augmentait selon le modèle suivant :

\[P(t)=316e^{0.0074t}, \nonumber \]

où$P$ se mesure en millions de personnes et$t$ dans les années postérieures à 2013.

a. Sur la base de ce modèle, quelle sera la population des États-Unis en 2020 ?

b. Déterminez quand la population des États-Unis sera le double de ce qu'elle est en 2013.

Réponse: a.$\sim 333$ millions
b. 94 ans à partir de 2013, ou en 2017

78) [T] Le montant$A$ accumulé après que les$1000$ dollars ont été investis pendant des$t$ années à un taux d'intérêt de 4 % est modélisé par la fonction$A(t)=1000(1.04)^t$.

a. Déterminez le montant accumulé après des$5$ années et des$10$ années.

b. Déterminez combien de temps il faut pour que l'investissement initial triple.

79) [T] On sait qu'une colonie bactérienne cultivée en laboratoire double en quelques$12$ heures. Supposons qu'au départ, des$1000$ bactéries soient présentes.

a. Utilisez la fonction exponentielle$Q=Q_0e^{kt}$ pour déterminer la valeur$k$, qui est le taux de croissance de la bactérie. Arrondir à la quatrième décimale.

b. Déterminez approximativement le temps nécessaire à la croissance$200,000$ des bactéries.

Réponse: a.$k≈0.0578$
b. ≈$92$ heures

80) [T] La population de lapins dans une réserve animalière double tous les$6$ mois. Supposons qu'il y ait eu$120$ des lapins

a. Utilisez la fonction exponentielle$P=P_0a^t$ pour déterminer la constante du taux de croissance$a$. Arrondir à la quatrième décimale.

b. Utilisez la fonction de la partie a. pour déterminer approximativement combien de temps il faut pour que la population de lapins atteigne 3 500.

81) [T] Le tremblement de terre de 1906 à San Francisco avait une magnitude de 8,3 sur l'échelle de Richter. Dans le même temps, au Japon, un tremblement de terre de magnitude 4,9 n'a causé que des dégâts mineurs. Environ combien d'énergie supplémentaire a été libérée par le tremblement de terre de San Francisco par rapport au tremblement de terre japonais ?

Réponse: Le tremblement de terre de San Francisco a produit$10^{3.4}$ ou$\sim 2512$ fois plus d'énergie que le tremblement de terre du Japon.

Contributeurs

Template:ContribOpenStaxCalc