1.5 : Fonctions exponentielles et logarithmiques
- Page ID
- 197942
- Identifiez la forme d'une fonction exponentielle.
- Expliquez la différence entre les graphiques de\(x^{b}\) et\(b^{x}\).
- Reconnaissez l'importance du chiffre\(e\).
- Identifiez la forme d'une fonction logarithmique.
- Expliquer la relation entre les fonctions exponentielles et logarithmiques.
- Décrire comment calculer un logarithme sur une base différente.
- Identifiez les fonctions hyperboliques, leurs graphes et leurs identités de base.
Dans cette section, nous examinons les fonctions exponentielles et logarithmiques. Nous utilisons les propriétés de ces fonctions pour résoudre des équations impliquant des termes exponentiels ou logarithmiques, et nous étudions la signification et l'importance du nombre\(e\). Nous définissons également des fonctions hyperboliques et hyperboliques inverses, qui impliquent des combinaisons de fonctions exponentielles et logarithmiques. (Notez que nous présentons des définitions alternatives des fonctions exponentielles et logarithmiques dans le chapitre Applications des intégrations, et que nous prouvons que les fonctions ont les mêmes propriétés quelle que soit la définition.)
Fonctions exponentielles
Les fonctions exponentielles apparaissent dans de nombreuses applications. La croissance démographique en est un exemple courant. Par exemple, si une population commence par\(P_0\) des individus puis croît à un rythme annuel de\(2\%\), sa population après un an est
\[P(1)=P_0+0.02P_0=P_0(1+0.02)=P_0(1.02).\nonumber \]
Sa population après 2 ans est
\[P(2)=P(1)+0.02P(1)=P(1)(1.02)=P_0(1.02)^2.\nonumber \]
En général, sa population après des\(t\) années est
\[P(t)=P_0(1.02)^t,\nonumber \]
qui est une fonction exponentielle. Plus généralement, toute fonction de la forme\(f(x)=b^x\), où\(b>0\)\(b≠1\), est une fonction exponentielle avec une base\(b\) et un exposant Les fonctions\(x.\) exponentielles ont des bases constantes et des exposants variables. Notez qu'une fonction de la forme\(f(x)=x^b\) d'une constante n'\(b\)est pas une fonction exponentielle mais une fonction de puissance.
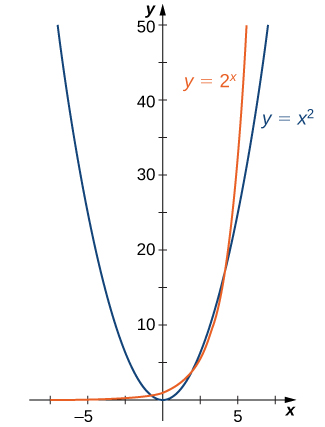
Pour voir la différence entre une fonction exponentielle et une fonction de puissance, nous comparons les fonctions\(y=x^2\) et\(y=2^x\). Dans le tableau\(\PageIndex{1}\), nous voyons les deux\(2^x\) et nous\(x^2\) approchons de l'infini comme\(x→∞\). Finalement, cependant,\(2^x\) devient plus grand que\(x^2\) et croît plus rapidement que\(x→∞\). Dans la direction opposée, comme\(x→−∞\)\(x^2→∞\), tandis que\(2^x→0\). La ligne\(y=0\) est une asymptote horizontale pour\(y=2^x\).
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x^2\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| \(2^x\) | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
Dans la figure\(\PageIndex{1}\), nous représentons les deux\(y=x^2\) et\(y=2^x\) montrons en quoi les graphiques diffèrent.
Évaluation des fonctions exponentielles
Rappelons les propriétés des exposants : s'il s'\(x\)agit d'un entier positif, alors nous le définissons\(b^x=b⋅b⋯b\) (avec des\(x\) facteurs de\(b\)). Si\(x\) est un entier négatif, alors\(x=−y\) pour un entier positif\(y\), et nous définissons\(b^x=b^{−y}=1/b^y\). En outre,\(b^0\) est défini comme étant\(1\). Si\(x\) est un nombre rationnel, alors\(x=p/q\), où\(p\) et\(q\) sont des nombres entiers et\(b^x=b^{p/q}=\sqrt[q]{b^p}\). Par exemple,\(9^{3/2}=\sqrt{9^3}=\left(\sqrt{9}\right)^3=27\). Cependant, comment\(b^x\) définit-on s'il s'\(x\)agit d'un nombre irrationnel ? Par exemple, qu'entendons-nous par\(2^{\sqrt{2}}\) ? Il s'agit d'une question trop complexe pour que nous puissions y répondre pleinement dès maintenant ; toutefois, nous pouvons faire une approximation.
| \(x\) | 1.4 | 1,41 | 1,414 | 1.4142 | 1.41421 | 1.414 213 |
|---|---|---|---|---|---|---|
| \(2^x\) | 2.639 | 2,65 737 | 2.66475 | 2.665119 | 2.665138 | 2.665143 |
Dans le tableau\(\PageIndex{2}\), nous listons certains nombres rationnels approchant\(\sqrt{2}\), et les valeurs de\(2^x\) pour chaque nombre rationnel\(x\) sont également présentées. Nous prétendons que si nous choisissons des nombres rationnels qui\(x\) se rapprochent de plus en plus\(\sqrt{2}\), les valeurs de\(2^x\) se rapprochent de plus en plus d'un certain nombre\(L\). Nous définissons ce nombre\(L\) comme étant\(2^{\sqrt{2}}\).
Supposons qu'une population particulière de bactéries soit connue pour doubler de taille toutes les\(4\) heures. Si une culture commence avec des\(1000\) bactéries, le nombre de bactéries après les\(4\) heures de culture est de\(n(4)=1000⋅2\). Le nombre de bactéries après les\(8\) heures de travail est de\(n(8)=n(4)⋅2=1000⋅2^2\). En général, le nombre de bactéries après les\(4m\) heures de travail est de\(n(4m)=1000⋅2^m\). En\(t=4m\) regardant, on voit que le nombre de bactéries après t heures est de\(n(t)=1000⋅2^{t/4}\). Déterminez le nombre de bactéries après des\(6\) heures, des\(10\) heures et des\(24\) heures.
Solution
Le nombre de bactéries après 6 heures est donné par
\[n(6)=1000⋅2^{6/4}≈2828\, \text{bacteria}. \nonumber \]
Le nombre de bactéries après les\(10\) heures de travail est donné par
\[n(10)=1000⋅2^{10/4}≈5657\, \text{bacteria}. \nonumber \]
Le nombre de bactéries après les\(24\) heures de travail est donné par\(n(24)=1000⋅2^6=64,000\) les bactéries.
Compte tenu de la fonction exponentielle\(f(x)=100⋅3^{x/2}\), évaluez\(f(4)\) et\(f(10)\).
- Réponse
-
\(f(4)=900\)
\(f(10)=24,300\).
Représentation graphique de fonctions exponentielles
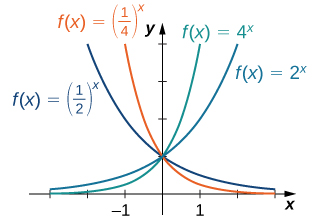
Pour toute base\(b>0\)\(b≠1\), la fonction exponentielle\(f(x)=b^x\) est définie pour tous les nombres réels\(x\) et\(b^x>0\). Par conséquent, le domaine de\(f(x)=b^x\) est\((−∞,∞)\) et la gamme est\((0,∞)\). Pour représenter\(b^x\) graphiquement, nous remarquons que pour\(b>1\),\(b^x\) augmente au\(b^x→∞\) fur\((−∞,∞)\) et à mesure\(x→∞\), alors que\(b^x→0\) comme\(x→−∞\). D'autre part, si\(0<b<1\),\(f(x)=b^x\) est décroissant au\(b^x→0\) fur\((−∞,∞)\) et à\(b^x→∞\) mesure\(x→∞\) que\(x→−∞\) (Figure\(\PageIndex{2}\)).
Notez que les fonctions exponentielles satisfont aux lois générales des exposants. Pour vous rappeler ces lois, nous les énonçons sous forme de règles.
Pour toutes les constantes\(a>0\)\(b>0\), et pour toutes\(x\)\(y,\)
- \[b^x⋅b^y=b^{x+y} \nonumber \]
- \[\dfrac{b^x}{b^y}=b^{x−y} \nonumber \]
- \[(b^x)^y=b^{xy} \nonumber \]
- \[(ab)^x=a^xb^x \nonumber \]
- \[\dfrac{a^x}{b^x}=\left(\dfrac{a}{b}\right)^x \nonumber \]
Utilisez les lois des exposants pour simplifier chacune des expressions suivantes.
- \(\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}\)
- \(\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}\)
Solution
a. Nous pouvons simplifier comme suit :
\[\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}=\dfrac{2^3(x^{2/3})^3}{4^2(x^{−1/3})^2}= \dfrac{8x^2}{16x^{−2/3}} =\dfrac{x^2x^{2/3}}{2}=\dfrac{x^{8/3}}{2}. \nonumber \]
b. Nous pouvons simplifier comme suit :
\[\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}=\dfrac{(x^3)^2(y^{−1})^2}{x^{−2}(y^2)^{−2}}=\dfrac{x^6y^{−2}}{x^{−2}y^{−4}} =x^6x^2y^{−2}y^4=x^8y^2. \nonumber \]
Utilisez les lois des exposants pour simplifier\(\dfrac{6x^{−3}y^2}{12x^{−4}y^5}\).
- Allusion
-
\(x^a/x^b=x^{a-b}\)
- Réponse
-
\(x/(2y^3)\)
Le numéro e
Un type spécial de fonction exponentielle apparaît fréquemment dans les applications du monde réel. Pour le décrire, prenons l'exemple suivant de croissance exponentielle, qui résulte de l'intérêt composé sur un compte d'épargne. Supposons qu'une personne\(P\) investisse des dollars dans un compte d'épargne avec un taux d'intérêt annuel\(r\), composé chaque année. Le montant d'argent après 1 an est
\(A(1)=P+rP=P(1+r)\).
Le montant d'argent après des\(2\) années est
\(A(2)=A(1)+rA(1)=P(1+r)+rP(1+r)=P(1+r)^2\).
Plus généralement, le montant après des\(t\) années est
\(A(t)=P(1+r)^t\).
Si l'argent est composé 2 fois par an, le montant d'argent après six mois est
\(A\left(\dfrac{1}{2}\right)=P+\left(\dfrac{r}{2}\right)P=P\left(1+\left(\dfrac{r}{2}\right)\right)\).
Le montant d'argent après\(1\) année est
\(A(1)=A\left(\dfrac{1}{2}\right)+\left(\dfrac{r}{2}\right)A \left(\dfrac{1}{2}\right)=P\left(1+\dfrac{r}{2}\right)+\dfrac{r}{2}\left(\left(P(1+\dfrac{r}{2}\right)\right)=P\left(1+\dfrac{r}{2}\right)^2.\)
Après des\(t\) années, le montant d'argent sur le compte est
\(A(t)=P\left(1+\dfrac{r}{2}\right)^{2t}\).
Plus généralement, si l'argent est composé\(n\) plusieurs fois par an, le montant d'argent sur le compte après des\(t\) années est donné par la fonction
\(A(t)=P\left(1+\dfrac{r}{n}\right)^{nt}.\)
Que se passe-t-il alors que\(n→∞?\) Pour répondre à cette question, nous laissons\(m=n/r\) et écrivons
\(\left(1+\dfrac{r}{n}\right)^{nt}=\left(1+\dfrac{1}{m}\right)^{mrt},\)
et examinez le comportement de\((1+1/m)^m\) as\(m→∞\) à l'aide d'une table de valeurs (Table\(\PageIndex{3}\)).
| \(m\) | 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 |
|---|---|---|---|---|---|---|
| \(\left(1+\dfrac{1}{m}\right)^m\) | 2,5937 | 2,7048 | 2.71692 | 2.71815 | 2.718 268 | 2.718 280 |
En regardant ce tableau, il semble qu'il\((1+1/m)^m\) se rapproche d'un nombre compris entre\(2.7\) et\(2.8\) as\(m→∞\). En\((1+1/m)^m\) fait, s'approche d'un certain nombre comme\(m→∞\). C'est ce numéro que nous appelons\(e\). Jusqu'à six décimales de précision,
\[e≈2.718282. \nonumber \]
La lettre\(e\) a été utilisée pour la première fois pour représenter ce nombre par le mathématicien suisse Leonhard Euler dans les années 1720. Bien qu'Euler n'ait pas découvert le nombre, il a montré de nombreux liens importants entre les fonctions logarithmiques\(e\) et les fonctions logarithmiques. Nous utilisons encore la notation\(e\) aujourd'hui pour honorer le travail d'Euler, car elle apparaît dans de nombreux domaines des mathématiques et parce que nous pouvons l'utiliser dans de nombreuses applications pratiques.
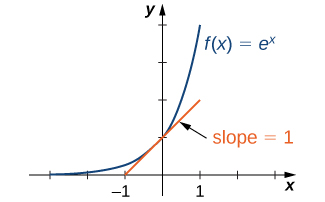
Pour en revenir à notre exemple de compte d'épargne, nous pouvons conclure que si une personne place des\(P\) dollars dans un compte à un taux d'intérêt annuel\(r\), composé de façon continue, alors\(A(t)=Pe^{rt}\). Cette fonction peut vous être familière. Comme les fonctions impliquant une base\(e\) apparaissent souvent dans les applications, nous\(f(x)=e^x\) les appelons fonction exponentielle naturelle. Non seulement cette fonction est intéressante en raison de la définition du nombre\(e\), mais aussi, comme nous le verrons plus loin, son graphe possède une propriété importante.
Depuis\(e>1\), nous savons que cela\(f(x) = e^x\) ne cesse de croître\((−∞,∞)\). Dans la figure\(\PageIndex{3}\), nous montrons un graphique\(f(x)=e^x\) avec une ligne tangente au graphe de\(f\) at\(x=0\). Nous donnons une définition précise de la tangente dans le chapitre suivant ; mais, de manière informelle, nous disons qu'une droite tangente à un graphe de\(f\) at\(x=a\) est une droite qui passe par le point\((a,f(a))\) et a la même « pente » qu'\(f\)à ce point. La fonction\(f(x)=e^x\) est la seule fonction exponentielle\(b^x\) avec une ligne tangente à\(x=0\) qui a une pente de\(1.\) Comme nous le verrons plus loin dans le texte, avoir cette propriété fait de la fonction exponentielle naturelle la fonction exponentielle la plus simple à utiliser dans de nombreux cas.
Supposons qu'\($500\)il soit investi dans un compte à un taux d'intérêt annuel de\(r=5.5\%\), composé en continu.
- \(t\)Soit le nombre d'années suivant l'investissement initial et\(A(t)\) le montant d'argent sur le compte à ce moment\(t\). Trouvez une formule pour\(A(t)\).
- Trouvez le montant d'argent sur le compte après des\(10\) années et après des\(20\) années.
Solution
a. Si des\(P\) dollars sont investis dans un compte à un taux d'intérêt annuel\(r\), composé de façon continue, alors\(A(t)=Pe^{rt}\). Ici\(P=$500\) et\(r=0.055\). Par conséquent,\(A(t)=500e^{0.055t}\).
b. Après des\(10\) années, le montant d'argent sur le compte est
\(A(10)=500e^{0.055⋅10}=500e^{0.55}≈$866.63\).
Après des\(20\) années, le montant d'argent sur le compte est
\(A(20)=500e^{0.055⋅20}=500e^{1.1}≈$1,502.08\).
Si vous êtes\($750\) investi dans un compte à un taux d'intérêt annuel de\(4\%\), composé en continu, trouvez une formule pour le montant d'argent sur le compte après des\(t\) années. Trouvez le montant d'argent après des\(30\) années.
- Allusion
-
\(A(t)=Pe^{rt}\)
- Réponse
-
\(A(t)=750e^{0.04t}\). Après des\(30\) années, il y aura environ\($2,490.09\).
Fonctions logarithmiques
En utilisant notre compréhension des fonctions exponentielles, nous pouvons discuter de leurs inverses, qui sont les fonctions logarithmiques. Ils sont utiles lorsque nous devons prendre en compte tout phénomène qui varie sur une large gamme de valeurs, comme l'échelle du pH en chimie ou les décibels dans les niveaux sonores.
La fonction exponentielle\(f(x)=b^x\) est univoque, avec domaine\((−∞,∞)\) et plage\((0,∞)\). Elle possède donc une fonction inverse, appelée fonction logarithmique avec base\(b\). Pour tout\(b>0,\, b≠1\), la fonction logarithmique avec base\(b\), notée\(\log_b\), possède un domaine\((0,∞)\) et une plage\((−∞,∞)\), et satisfait
\[\log_b(x)=y \nonumber \]
si et seulement si\(b^y=x\).
Par exemple,
\[\log_2(8)=3\nonumber \]
depuis\(2^3=8\),
\[\log_{10}\left(\dfrac{1}{100}\right)=−2 \nonumber \]
depuis\(10^{−2}=\dfrac{1}{10^2}=\dfrac{1}{100}\),
\[\log_b(1)=0 \nonumber \]
depuis\(b^0=1\) pour n'importe quelle base\(b>0\).
De plus, étant donné que\(y=\log_b(x)\) et\(y=b^x\) sont des fonctions inverses,
\[\log_b(b^x)=x \nonumber \]
et
\[b^{\log_b(x)}=x. \nonumber \]
La fonction logarithmique la plus couramment utilisée est la fonction\(\log_e\). Comme cette fonction utilise\(e\) le naturel comme base, elle est appelée logarithme naturel. Ici, nous utilisons la notation\(\ln (x)\) ou\(\ln x\) pour signifier\(\log_e(x)\). Par exemple,
\[ \begin{align*} \ln (e) &=\log_e(e)=1 \\[4pt] \ln (e^3) &=\log_e(e^3)=3 \\[4pt] \ln (1) &=\log_e(1)=0. \end{align*}\]
Étant donné que les fonctions\(f(x)=e^x\) et\(g(x)=\ln (x)\) sont inversées,
\(\ln (e^x)=x\)et\(e^{\ln x}=x\),
et leurs graphes sont symétriques par rapport à la ligne\(y=x\) (Figure\(\PageIndex{4}\)).
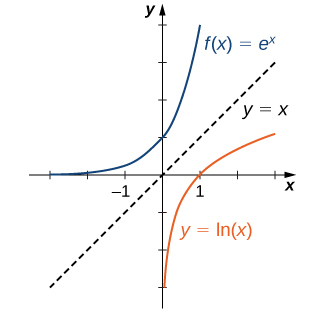
En général, quelle que soit la base\(b>0\)\(b≠1\), la fonction\(g(x)=\log_b(x)\) est symétrique par rapport à la ligne\(y=x\) avec la fonction\(f(x)=b^x\). En utilisant ce fait et les graphes des fonctions exponentielles, nous tracons des fonctions\(\log_b\) pour plusieurs valeurs de\(b>1\) (Figure\(\PageIndex{5}\)).
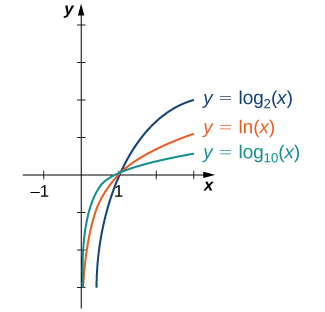
Avant de résoudre certaines équations impliquant des fonctions exponentielles et logarithmiques, passons en revue les propriétés de base des logarithmes.
Si\(a,\,b,\,c>0,\,b≠1\) et\(r\) est un nombre réel, alors
- Propriété du produit
\[\log_b(ac)=\log_b(a)+\log_b(c) \label{productprop} \]
- Propriété du quotient
\[\log_b \left(\dfrac{a}{c} \right)=\log_b(a)−\log_b(c) \label{quotientprop} \]
- Propriété énergétique
\[\log_b(a^r)=r\log_b(a) \label{powerprop} \]
Résolvez chacune des équations suivantes pour\(x\).
- \(5^x=2\)
- \(e^x+6e^{−x}=5\)
Solution
a. En appliquant la fonction du logarithme naturel aux deux côtés de l'équation, nous avons
\(\ln 5^x=\ln 2\).
En utilisant la propriété de puissance des logarithmes,
\(x\ln 5=\ln 2.\)
Par conséquent,
\[x= \dfrac{\ln 2}{\ln 5}. \nonumber \]
b. En multipliant les deux côtés de l'équation par\(e^x\), nous arrivons à l'équation
\(e^{2x}+6=5e^x\).
Réécrire cette équation comme
\(e^{2x}−5e^x+6=0\),
nous pouvons ensuite la réécrire sous forme d'équation quadratique dans\(e^x\) :
\((e^x)^2−5(e^x)+6=0.\)
Nous pouvons maintenant résoudre l'équation quadratique. En factorisant cette équation, nous obtenons
\((e^x−3)(e^x−2)=0.\)
Par conséquent, les solutions répondent à\(e^x=3\) et\(e^x=2\). Le logarithme naturel des deux côtés nous donne les solutions\(x=\ln 3,\ln 2\).
Résoudre
\[e^{2x}/(3+e^{2x})=1/2. \nonumber \]
- Allusion
-
Résolvez d'abord l'équation pour\(e^{2x}\)
- Réponse
-
\(x=\dfrac{\ln 3}{2}\).
Résolvez chacune des équations suivantes pour\(x\).
- \(\ln \left(\dfrac{1}{x}\right)=4\)
- \(\log_{10}\sqrt{x}+\log_{10}x=2\)
- \(\ln (2x)−3\ln (x^2)=0\)
Solution
a. Selon la définition de la fonction logarithmique naturelle,
\(\ln \left(\dfrac{1}{x} \right)=4\)
- si et seulement si\(e^4=\dfrac{1}{x}\).
Par conséquent, la solution est\(x=1/e^4\).
b. À l'aide des propriétés de produit (équation \ ref {productprop}) et de puissance (équation \ ref {powerprop}) des fonctions logarithmiques, réécrivez le côté gauche de l'équation comme
\[\begin{align*} \log_{10}\sqrt{x} + \log_{10}x &= \log_{10} x \sqrt{x} \\[4pt] &= \log_{10}x^{3/2} \\[4pt] &= \dfrac{3}{2}\log_{10}x. \end{align*}\]
Par conséquent, l'équation peut être réécrite comme
\(\dfrac{3}{2}\log_{10}x=2\)
ou
\(\log_{10}x=\dfrac{4}{3}\).
La solution est\(x=10^{4/3}=10\sqrt[3]{10}\).
c. En utilisant la propriété de puissance (équation \ ref {powerprop}) des fonctions logarithmiques, nous pouvons réécrire l'équation comme suit\(\ln (2x)−\ln (x^6)=0\) :
En utilisant la propriété du quotient (Equation \ ref {quotientprop}), cela devient
\(\ln \left(\dfrac{2}{x^5}\right)=0\)
Donc\(2/x^5=1\), ce qui implique\(x=\sqrt[5]{2}\). Nous devons ensuite vérifier la présence de toute solution superflue.
Résoudre\(\ln (x^3)−4\ln (x)=1\).
- Allusion
-
Utilisez d'abord la propriété power, puis la propriété de produit des logarithmes.
- Réponse
-
\(x=\dfrac{1}{e}\)
Lorsque vous évaluez une fonction logarithmique à l'aide d'une calculatrice, vous avez peut-être remarqué que les seules options sont\(\log_{10}\) ou\(\log\), appelé logarithme commun\(\ln\), ou, qui est le logarithme naturel. Cependant, les fonctions exponentielles et les fonctions logarithmiques peuvent être exprimées en termes de n'importe quelle base souhaitée\(b\). Si vous devez utiliser une calculatrice pour évaluer une expression avec une base différente, vous pouvez d'abord appliquer les formules de changement de base. En utilisant ce changement de base, nous écrivons généralement une fonction exponentielle ou logarithmique donnée en termes de fonctions exponentielle naturelle et logarithmique naturelle.
Laissez\(a>0,\,b>0\), et\(a≠1,\,b≠1\).
1. \(a^x=b^{x \log_ba}\)pour n'importe quel nombre réel\(x\).
Si\(b=e\), cette équation se réduit à\(a^x=e^{x \log_ea}=e^{x \ln a}\).
2. \(\log_ax=\dfrac{\log_bx}{\log_ba}\)pour n'importe quel nombre réel\(x>0\).
Si\(b=e\), cette équation se réduit à\(\log_ax=\dfrac{\ln x}{\ln a}\).
Pour la première formule de changement de base, nous commençons par utiliser la propriété de puissance des fonctions logarithmiques. Nous le savons pour toutes les bases\(b>0,\, b≠1\),\(\log_b(a^x)=x \log_ba\). Par conséquent,
\(b^{\log_b(a^x)}\)=\(b^{x \log_ba}\).
De plus, nous le savons\(b^x\) et nous sommes\(\log_b(x)\) des fonctions inverses. Par conséquent,
\(b^{\log_b(a^x)}=a^x\).
En combinant ces deux dernières égalités, nous en arrivons à la conclusion suivante\(a^x=b^{x \log_ba}\).
Pour prouver la deuxième propriété, nous montrons que
\((\log_ba)⋅(\log_ax)=\log_bx.\)
Laissez\(u=\log_ba,v=\log_ax\), et\(w=\log_bx\). Nous allons le montrer\(u⋅v=w\). Par la définition des fonctions logarithmiques, nous savons que\(b^u=a,\, a^v=x\), et\(b^w=x\). D'après les équations précédentes, nous voyons que
\(b^{uv}=(b^u)^v=a^v=x=b^w.\)
Par conséquent,\(b^{uv}=b^w\). Puisque les fonctions exponentielles sont univoques, nous pouvons en conclure que\(u⋅v=w\).
\(\square\)
Utilisez un utilitaire de calcul pour effectuer une évaluation\(\log_37\) à l'aide de la formule de changement de base présentée précédemment.
Solution
Utilisez la deuxième équation avec\(a=3\) et\(b=e\) :\(\log_37=\dfrac{\ln 7}{\ln 3}≈1.77124\).
Utilisez la formule de changement de base et un utilitaire de calcul pour évaluer\(\log_46\).
- Allusion
-
Utilisez le changement de base pour réécrire cette expression en termes d'expressions impliquant la fonction logarithme naturel.
- Réponse
-
\(\log_46 = \dfrac{\ln 6}{\ln 4} \approx 1.29248\)
En 1935, Charles Richter a développé une échelle (aujourd'hui connue sous le nom d'échelle de Richter) pour mesurer l'ampleur d'un tremblement de terre. L'échelle est une échelle logarithmique de base 10, et elle peut être décrite comme suit : considérez un tremblement de terre de magnitude\(R_1\) sur l'échelle de Richter et un second tremblement de terre de magnitude\(R_2\) sur l'échelle de Richter. Supposons\(R_1>R_2\), ce qui signifie que le tremblement de terre de magnitude\(R_1\) est plus fort, mais combien est-il plus fort que l'autre tremblement de terre ?

Un moyen de mesurer l'intensité d'un tremblement de terre consiste à utiliser un sismographe pour mesurer l'amplitude des ondes sismiques. Si\(A_1\) est l'amplitude mesurée pour le premier séisme et\(A_2\) l'amplitude mesurée pour le second séisme, alors les amplitudes et les magnitudes des deux séismes répondent à l'équation suivante :
\(R_1−R_2=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Prenons l'exemple d'un tremblement de terre de 8 sur l'échelle de Richter et d'un tremblement de terre de 7 sur l'échelle de Richter. Ensuite,
\(8−7=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Par conséquent,
\(\log_{10}\left(\dfrac{A1}{A2}\right)=1\),
ce qui implique\(A_1/A_2=10\) ou\(A_1=10A_2\). Comme\(A_1\) c'est 10 fois la taille de\(A_2\), nous disons que le premier tremblement de terre est 10 fois plus intense que le second. En revanche, si un séisme mesure 8 sur l'échelle de Richter et qu'un autre mesure 6, alors l'intensité relative des deux séismes satisfait à l'équation
\(\log_{10}\left(\dfrac{A1}{A2}\right)=8−6=2\).
Par conséquent\(A_1=100A_2\), le premier tremblement de terre est 100 fois plus intense que le second.
Comment pouvons-nous utiliser des fonctions logarithmiques pour comparer la gravité relative du séisme de magnitude 9 survenu au Japon en 2011 avec le séisme de magnitude 7,3 survenu en Haïti en 2010 ?
Solution
Pour comparer les tremblements de terre au Japon et en Haïti, nous pouvons utiliser une équation présentée précédemment :
\(9−7.3=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Par conséquent\(A_1/A_2=10^{1.7}\), et nous concluons que le tremblement de terre au Japon a été environ 50 fois plus intense que le tremblement de terre en Haïti.
Comparez la gravité relative d'un séisme de\(8.4\) magnitude à celle d'un séisme de\(7.4\) magnitude.
- Allusion
-
\(R_1−R_2=\log_{10}(A1/A2)\).
- Réponse
-
Le séisme de\(8.4\) magnitude est à peu près\(10\) deux fois plus grave que le séisme de\(7.4\) magnitude.
Fonctions hyperboliques
Les fonctions hyperboliques sont définies en fonction de certaines combinaisons de\(e^x\) et\(e^{−x}\). Ces fonctions apparaissent naturellement dans diverses applications d'ingénierie et de physique, notamment l'étude des vagues d'eau et des vibrations des membranes élastiques. Une autre utilisation courante d'une fonction hyperbolique est la représentation d'une chaîne ou d'un câble suspendu, également connu sous le nom de caténaire (Figure\(\PageIndex{7}\)). Si nous introduisons un système de coordonnées de telle sorte que le point bas de la chaîne se trouve le long de l'\(y\)axe, nous pouvons décrire la hauteur de la chaîne en termes de fonction hyperbolique. Nous définissons d'abord les fonctions hyperboliques.

Cosinus hyperbolique
\(\cosh x=\dfrac{e^x+e^{−x}}{2}\)
Sinus hyperbolique
\(\sinh x=\dfrac{e^x−e^{−x}}{2}\)
Tangente hyperbolique
\(\tanh x=\dfrac{\sinh x}{\cosh x}=\dfrac{e^x−e^{−x}}{e^x+e^{−x}}\)
Cosécant hyperbolique
\(\operatorname{csch}x=\dfrac{1}{\sinh x}=\dfrac{2}{e^x−e^{−x}}\)
Sécante hyperbolique
\(\operatorname{sech}x=\dfrac{1}{\cosh x}=\dfrac{2}{e^x+e^{−x}}\)
Cotangente hyperbolique
\(\coth x=\dfrac{\cosh x}{\sinh x}=\dfrac{e^x+e^{−x}}{e^x−e^{−x}}\)
Le nom\(\cosh\) rime avec « bon sang », alors que le nom\(\sinh\) se prononce « cinch ». \(\operatorname{Tanh}, \,\operatorname{sech}, \, \operatorname{csch},\)et\(\coth\) se prononcent respectivement « tanch », « seech », « coseech » et « cotanch ».
En utilisant la définition\(\cosh(x)\) et les principes de la physique, il peut être démontré que la hauteur d'une chaîne suspendue, telle que celle de la figure\(\PageIndex{8}\), peut être décrite par la fonction\(h(x)=a\cosh(x/a) + c\) pour certaines constantes\(a\) et\(c\).
Mais pourquoi ces fonctions sont-elles appelées fonctions hyperboliques ? Pour répondre à cette question, considérez la quantité\(\cosh^2 t − \sinh^2 t\). En utilisant la définition de\(\cosh\) et\(\sinh\), nous voyons que
\[\cosh^2 t − \sinh^2 t=\dfrac{e^{2t}+2+e^{−2t}}{4}−\dfrac{e^{2t}−2+e^{−2t}}{4}=1. \nonumber \]
Cette identité est l'analogue de l'identité trigonométrique\(\cos^2 t + \sin^2 t=1\). Ici, étant donné une valeur\(t\), le point\((x,y)=(\cosh t,\,\sinh t)\) se trouve sur l'hyperbole unitaire\(x^2−y^2=1\) (Figure\(\PageIndex{8}\)).
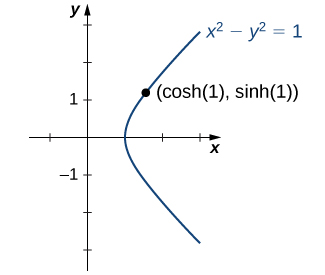
Graphiques des fonctions hyperboliques
Pour représenter\(\cosh x\) graphiquement et\(\sinh x\), nous utilisons le fait que les deux fonctions s'approchent\((1/2)e^x\) comme\(x→∞\), puisque\(e^{−x}→0\) comme\(x→∞\). Comme\(x→−∞,\cosh x\) des approches\(1/2e^{−x}\), alors que\(\sinh x\) des approches\(−1/2e^{−x}\). Par conséquent, en utilisant les graphes de\(1/2e^x,1/2e^{−x}\), et\(−1/2e^{−x}\) comme guides, nous graphions\(\cosh x\) et\(\sinh x\). Pour représenter\(\tanh x\) graphiquement, nous utilisons le fait que\(\tanh(0)=0\),\(−1<\tanh(x)<1\) pour tous\(x\), au\(\tanh x→1\)\(\tanh x→−1\) fur\(x→∞\) et à mesure\(x→−∞\). Les graphes des trois autres fonctions hyperboliques peuvent être esquissés à l'aide des graphes de\(\cosh x\)\(\sinh x\), et\(\tanh x\) (Figure\(\PageIndex{9}\)).
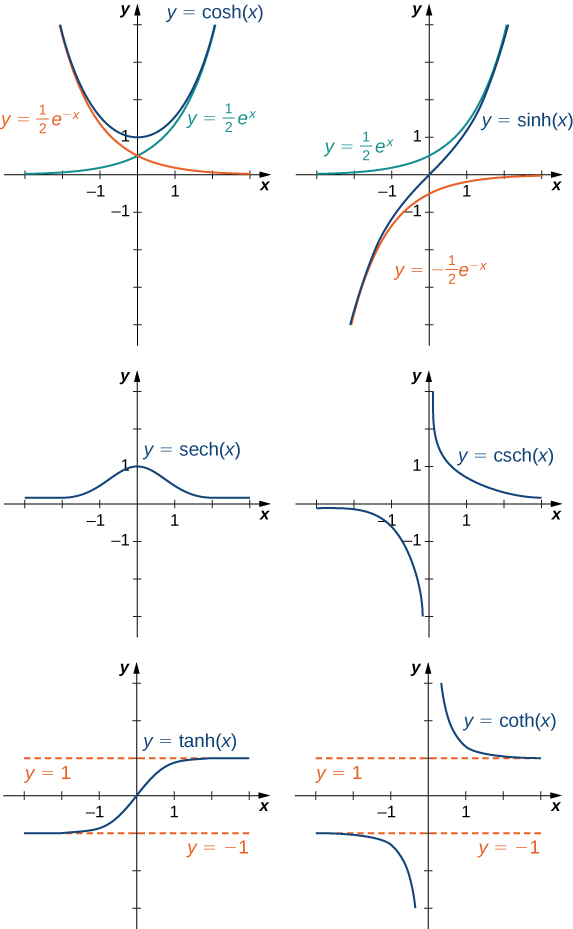
Identités impliquant des fonctions hyperboliques
L'identité\(\cosh^2 t−\sinh^2 t = 1\), illustrée dans la figure\(\PageIndex{8}\), est l'une des nombreuses identités impliquant les fonctions hyperboliques, dont certaines sont répertoriées ci-dessous. Les quatre premières propriétés découlent facilement des définitions du sinus hyperbolique et du cosinus hyperbolique. À l'exception de certaines différences de signes, la plupart de ces propriétés sont analogues aux identités des fonctions trigonométriques.
- \(\cosh(−x)=\cosh x\)
- \(\sinh(−x)=−\sinh x\)
- \(\cosh x+\sinh x=e^x\)
- \(\cosh x−\sinh x=e^{−x}\)
- \(\cosh^2 x−\sinh^2 x=1\)
- \(1−\tanh^2 x=\operatorname{sech}^2 x\)
- \(\coth^2 x −1=\operatorname{csch}^2 x\)
- \(\sinh(x±y)=\sinh x \cosh y ± \cosh x \sinh y\)
- \(\cosh(x±y)=\cosh x \cosh y ± \sinh x \sinh y\)
- Simplifiez\(\sinh(5\ln x)\).
- Si\(\sinh x=3/4\), trouvez les valeurs des cinq fonctions hyperboliques restantes.
Solution :
a. En utilisant la définition de la\(\sinh\) fonction, nous écrivons
\(\sinh(5\ln x)=\dfrac{e^{5\ln x}−e^{−5\ln x}}{2}=\dfrac{e^{\ln (x^5)}−e^{\ln (x^{−5})}}{2}=\dfrac{x^5−x^{−5}}{2}.\)
b. En utilisant l'identité\(\cosh^2 x − \sinh^2 x=1\), on constate que
\(\cosh^2 x=1+\left(\frac{3}{4}\right)^2=\dfrac{25}{16}.\)
Car\(\cosh x≥1\) pour tous\(x\), il le faut\(\cosh x=5/4\). Ensuite, en utilisant les définitions des autres fonctions hyperboliques, nous concluons que\(\tanh x=3/5,\operatorname{csch}x=4/3,\operatorname{sech}x=4/5\), et\(\coth x=5/3\).
Simplifiez\(\cosh(2\ln x)\).
- Allusion
-
Utilisez la définition de la\(\cosh\) fonction et la propriété de puissance des fonctions logarithmiques.
- Réponse
-
\((x^2+x^{−2})/2\)
Fonctions hyperboliques inverses
À partir des graphes des fonctions hyperboliques, nous voyons qu'elles sont toutes un-à-une sauf\(\cosh x\) et\(\operatorname{sech}x\). Si nous limitons les domaines de ces deux fonctions à l'intervalle\([0,∞),\), alors toutes les fonctions hyperboliques sont univoques et nous pouvons définir les fonctions hyperboliques inverses. Comme les fonctions hyperboliques impliquent elles-mêmes des fonctions exponentielles, les fonctions hyperboliques inverses impliquent des fonctions logarithmiques.
\ [\ begin {align*} & \ sinh^ {−1} x = \ operatorname {arcsinh} x= \ ln \ left (x+ \ sqrt {x^2+1} \ right) & & \ cosh^ {−1} x = \ operatorname {arccosh} x= \ ln \ left (x+ \ sqrt {x^2−1} \ right) \ [4 points]
& \ tanh^ {−1} x= \ operatorname {arctanh} x= \ dfrac {1} {2} \ ln \ left (\ dfrac {1+x} {1−x} \ right) & \ coth^ {−1} x = \ operatorname {arccot} x= \ frac {1} {2} \ ln \ left (\ dfrac {x+1} {x−1} \ right) \ \ [4pt]
& \ operatorname {sech} ^ {−1} x= \ operatorname {arcsech} x= \ ln \ left (\ dfrac {1+ \ sqrt {1−x^2}} {x} \ right) & & \ operatorname {csch} ^ {−1} x= \ operatorname {arccsch} x= \ ln \ left (\ dfrac {1} {x} + \ dfrac {\ sqrt {1+x^2}} {|x|} \ right) \ end { aligner*} \]
Voyons comment dériver la première équation. Les autres suivent de la même manière. Supposons\(y=\sinh^{−1}x\). Ensuite,\(x=\sinh y\) et, par la définition de la fonction sinusoïdale hyperbolique,\(x=\dfrac{e^y−e^{−y}}{2}\). Par conséquent,
\(e^y−2x−e^{−y}=0.\)
En multipliant cette équation par\(e^y\), nous obtenons
\(e^{2y}−2xe^y−1=0\).
Cela peut être résolu comme une équation quadratique, avec la solution
\(e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}=x±\sqrt{x^2+1}\).
Depuis\(e^y>0\), la seule solution est celle avec le signe positif. En appliquant le logarithme naturel aux deux côtés de l'équation, nous concluons que
\(y=\ln (x+\sqrt{x^2+1}).\)
Évaluez chacune des expressions suivantes.
\(\sinh^{−1}(2)\)
\(\tanh^{−1}(1/4)\)
Solution :
\[\sinh^{−1}(2)=\ln (2+\sqrt{2^2+1})=\ln (2+\sqrt{5})≈1.4436\nonumber \]
\[\tanh^{−1}(1/4)=\frac{1}{2}\ln \left(\dfrac{1+1/4}{1−1/4}\right)=\frac{1}{2}\ln \left(\dfrac{5/4}{3/4}\right)=\frac{1}{2}\ln \left(\dfrac{5}{3}\right)≈0.2554\nonumber \]
Évaluer\(\tanh^{−1}(1/2)\).
- Allusion
-
Utilisez la définition de\(\tanh^{−1}x\) et simplifiez.
- Réponse
-
\(\dfrac{1}{2}\ln (3)≈0.5493\).
Concepts clés
- La fonction exponentielle\(y=b^x\) augmente si\(b>1\) et diminue si\(0<b<1\). Son domaine est\((−∞,∞)\) et sa gamme est\((0,∞)\).
- La fonction logarithmique\(y=\log_b(x)\) est l'inverse de\(y=b^x\). Son domaine est\((0,∞)\) et sa gamme est\((−∞,∞).\)
- La fonction exponentielle naturelle est\(y=e^x\) et la fonction logarithmique naturelle est\(y=\ln x=\log_ex.\)
- Étant donné une fonction exponentielle ou une fonction logarithmique en base\(a\), nous pouvons modifier la base pour convertir cette fonction en n'importe quelle base\(b>0\),\(b≠1.\) nous la convertissons généralement en base\(e\).
- Les fonctions hyperboliques impliquent des combinaisons de fonctions exponentielles\(e^x\) et\(e^{−x}.\), par conséquent, les fonctions hyperboliques inverses impliquent le logarithme naturel.
Lexique
- base
- le nombre\(b\) dans la fonction exponentielle\(f(x)=b^x\) et la fonction logarithmique\(f(x)=\log_bx\)
- exposant
- la valeur\(x\) de l'expression\(b^x\)
- fonctions hyperboliques
- les fonctions désignées\(\sinh,\,\cosh,\,\operatorname{tanh},\,\operatorname{csch},\,\operatorname{sech},\) et\(\coth\), qui impliquent certaines combinaisons de\(e^x\) et\(e^{−x}\)
- fonctions hyperboliques inverses
- les inverses des fonctions hyperboliques où\(\cosh\) et\( \operatorname{sech}\) sont restreints au domaine\([0,∞)\) ; chacune de ces fonctions peut être exprimée en termes de composition de la fonction logarithmique naturelle et d'une fonction algébrique
- fonction exponentielle naturelle
- la fonction\(f(x)=e^x\)
- logarithme naturel
- la fonction\(\ln x=\log_ex\)
- numéro e
- au\(m\) fur et à mesure qu'elle augmente, la quantité\((1+(1/m)^m\) se rapproche d'un nombre réel ; nous définissons que ce nombre réel est\(e;\) la valeur de\(e\) est d'environ\(2.718282\)


