1.4E : Exercices pour la section 1.4

Last updated
Save as PDF

Page ID: 197984

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 6, utilisez le test de la ligne horizontale pour déterminer si chacun des graphiques donnés est un à un.

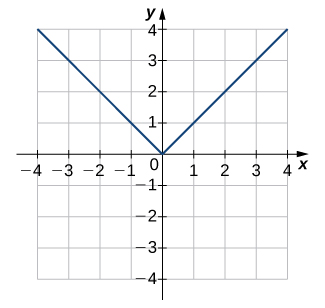
$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique est une fonction qui décroît en ligne droite jusqu'à l'origine, où elle commence à augmenter en ligne droite. L'intersection x et l'intersection y sont toutes deux à l'origine.$

Réponse: Pas en tête-à-tête

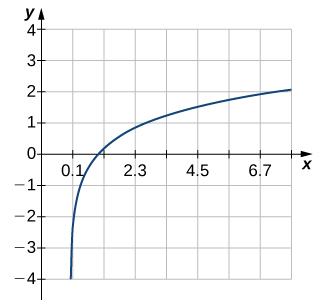
$Image d'un graphique. L'axe x va de 0 à 7 et l'axe y va de -4 à 4. Le graphique représente une fonction qui augmente constamment. Il y a une intersection X approximative au point (1, 0) et aucune intersection y n'est affichée.$

$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique présente une fonction qui ressemble à un demi-cercle, la moitié supérieure d'un cercle. La fonction commence au point (-3, 0) et augmente jusqu'au point (0, 3), où elle commence à diminuer jusqu'à se terminer au point (3, 0). Les points d'intersection x se situent à (-3, 0) et (3, 0). L'intersection y est à (0, 3).$

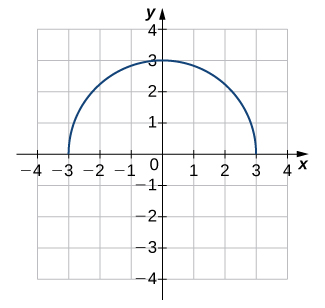
Réponse: Pas en tête-à-tête

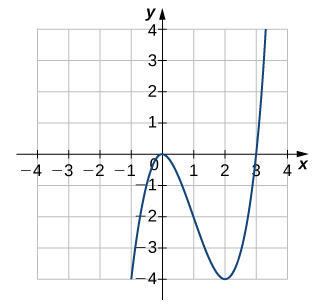
$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique présente une fonction courbe. La fonction augmente jusqu'à atteindre l'origine, puis diminue jusqu'à atteindre le point (2, -4), où elle recommence à augmenter. Il y a x points d'intersection à l'origine et au point (3, 0). L'intersection Y est à l'origine.$

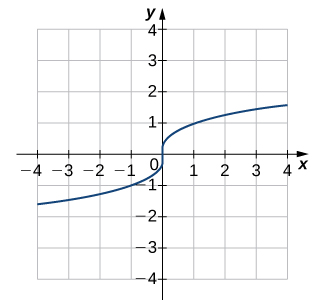
$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique présente une fonction courbe qui augmente constamment. L'intersection x et l'intersection y sont toutes deux à l'origine.$

Réponse: Un à un

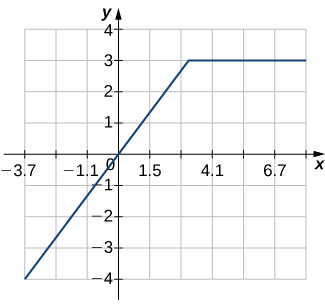
$Image d'un graphique. L'axe x va de -4 à 7 et l'axe y va de -4 à 4. Le graphique représente une fonction qui augmente en ligne droite jusqu'au point approximatif (, 3). Après ce point, la fonction prend la forme d'une ligne droite horizontale. L'intersection x et l'intersection y sont toutes deux à l'origine.$

Dans les exercices 7 à 12,

a. trouvez la fonction inverse, et

b. trouvez le domaine et la plage de la fonction inverse.

7)$f(x)=x^2−4, \quad x≥0$

Réponse: a.$f^{−1}(x)=\sqrt{x+4}$
b. Domaine :$x≥−4,$ Gamme :$y≥0$

8)$f(x)=\sqrt[3]{x−4}$

9)$f(x)=x^3+1$

Réponse: a.$f^{−1}(x)=\sqrt[3]{x−1}$
b. Domaine : tous les nombres réels, Intervalle : tous les nombres réels

10)$f(x)=(x−1)^2, \quad x≤1$

11)$f(x)=\sqrt{x−1}$

Réponse: a.$f^{−1}(x)=x^2+1$,
b. Domaine :$x≥0,$ Gamme :$y≥1$

(12)$f(x)=\dfrac{1}{x+2}$

Dans les exercices 13 à 16, utilisez le graphe de$f$ pour esquisser le graphe de sa fonction inverse.

13)

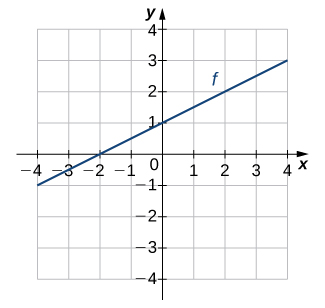
$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique représente une fonction linéaire croissante nommée « f » qui augmente toujours. L'intersection x est à (-2, 0) et l'intersection y à (0, 1).$

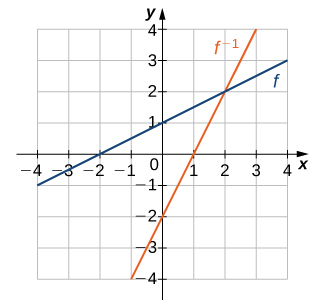
Réponse: $Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique comporte deux fonctions. La première fonction est une fonction linéaire croissante appelée « f ». L'intersection x est à (-2, 0) et l'intersection y à (0, 1). La deuxième fonction est une fonction linéaire croissante appelée « f inverse ». L'intersection x se trouve au point (1, 0) et l'intersection y est au point (0, -2).$

(14)

$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphique représente une fonction décroissante courbe appelée « f ». Lorsque la fonction diminue, elle se rapproche de l'axe X mais ne le touche jamais. La fonction n'a pas d'intersection x et l'intersection y est (0, 1).$

(15)

$Image d'un graphique. L'axe x s'étend de -8 à 8 et l'axe y va de -8 à 8. Le graphique représente une fonction linéaire croissante appelée « f ». La fonction commence au point (0, 1) et augmente en ligne droite jusqu'au point (4, 6). Après ce point, la fonction continue d'augmenter, mais à un rythme plus lent qu'auparavant, à mesure qu'elle s'approche du point (8, 8). La fonction n'a pas d'intersection x et l'intersection y est (0, 1).$

Réponse: $alt$

16)

$Image d'un graphique. L'axe x va de -4 à 4 et l'axe y va de -4 à 4. Le graphe représente une fonction courbe décroissante appelée « f », qui se termine à l'origine, qui est à la fois l'intersection x et l'intersection y. Un autre point de la fonction est (-4, 2).$

Dans les exercices 17 à 24, utilisez la composition pour déterminer quelles paires de fonctions sont inverses.

17)$f(x)=8x, \quad g(x)=\dfrac{x}{8}$

Réponse: Ce sont des inverses.

18)$f(x)=8x+3, \quad g(x)=\dfrac{x-3}{8}$

19)$f(x)=5x−7, \quad g(x)=\dfrac{x+5}{7}$

Réponse: Ce ne sont pas des inverses.

(20)$f(x)=\frac{2}{3}x+2, \quad g(x)=\frac{3}{2}x+3$

(21)$f(x)=\dfrac{1}{x−1}, \;x≠1, \quad g(x)=\dfrac{1}{x}+1,\; x≠0$

Réponse: Ce sont des inverses.

(22)$f(x)=x^3+1,\quad g(x)=(x−1)^{1/3}$

23)$f(x)=x^2+2x+1,\; x≥−1, \quad g(x)=−1+\sqrt{x},\; x≥0$

Réponse: Ce sont des inverses.

(24)$f(x)=\sqrt{4−x^2},\; 0≤x≤2, \quad g(x)=\sqrt{4−x^2},\; 0≤x≤2$

Dans les exercices 25 à 33, évaluez les fonctions. Donnez la valeur exacte.

25)$\tan^{−1}\left(\frac{\sqrt{3}}{3}\right)$

Réponse: $\frac{π}{6}$

(26)$\cos^{−1}\left(−\frac{\sqrt{2}}{2}\right)$

(27)$\cot^{−1}(1)$

Réponse: $\frac{π}{4}$

(28)$\sin^{−1}(−1)$

(29)$\cos^{−1}\left(\frac{\sqrt{3}}{2}\right)$

Réponse: $\frac{π}{6}$

(30)$\cos\big(\tan^{−1}(\sqrt{3})\big)$

31)$\sin\left(\cos^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)$

Réponse: $\frac{\sqrt{2}}{2}$

32)$\sin^{−1}\left(\sin\left(\frac{π}{3}\right)\right)$

33)$\tan^{−1}\left(\tan\left(−\frac{π}{6}\right)\right)$

Réponse: $-\frac{π}{6}$

34) La fonction$C=T(F)=(5/9)(F−32)$ convertit les degrés Fahrenheit en degrés Celsius.

a) Trouvez la fonction inverse$F=T^{−1}(C)$

b) À quoi sert la fonction inverse ?

35) [T] La vitesse$V$ (en centimètres par seconde) du sang dans une artère à une distance de$x$ cm du centre de l'artère peut être modélisée par la fonction$V=f(x)=500(0.04−x^2)$ de$0≤x≤0.2.$

a) Trouver$x=f^{−1}(V).$

b) Interprétez à quoi sert la fonction inverse.

c) Déterminez la distance par rapport au centre d'une artère à une vitesse de 15 cm/sec, 10 cm/sec et 5 cm/sec.

Réponse: a.$x=f^{−1}(V)=\sqrt{0.04−\dfrac{V}{500}}$
b. La fonction inverse détermine la distance par rapport au centre de l'artère à laquelle le sang circule avec une vitesse$V.$
d'environ 0,1 cm ; 0,14 cm ; 0,17 cm

36) Une fonction qui permet de convertir les tailles de robe aux États-Unis à celles en Europe est donnée par$D(x)=2x+24.$

a) Trouvez les tailles de robe européennes qui correspondent aux tailles 6, 8, 10 et 12 aux États-Unis.

b) Trouvez la fonction qui convertit les tailles de robe européennes en tailles de robe américaines.

c) Utilisez la partie b. pour trouver les tailles de robe aux États-Unis qui correspondent à 46, 52, 62 et 70.

37) [T] Le coût de l'élimination d'une toxine d'un lac est modélisé par la fonction$C(p)=\dfrac{75p}{85−p},$ où$C$ est le coût (en milliers de dollars) et$p$ la quantité de toxine dans un petit lac (mesurée en parties par milliard [ppb]). Ce modèle n'est valide que lorsque la quantité de toxine est inférieure à 85 ppb.

a) Déterminez le coût de l'élimination de 25 ppb, 40 ppb et 50 ppb de la toxine du lac.

b) Trouvez la fonction inverse.

c) Utilisez la partie b. pour déterminer la quantité de toxine éliminée pour 50 000$.

Réponse: a. 31 250 dollars, 66 667 dollars, 107 143 dollars
b.$p=\dfrac{85C}{C+75}$
c. 34 ppb

38) [T] Une voiture de course accélère à une vitesse donnée par$v(t)=\frac{25}{4}t+54,$

où$v$ est la vitesse (en pieds par seconde) à la fois$t.$

a) Détermine la vitesse de la voiture à 10 secondes.

b) Trouvez la fonction inverse.

c) Utilisez la partie b. pour déterminer le temps qu'il faut à la voiture pour atteindre une vitesse de 150 pieds/sec.

39) [T] Le nombre de Mach d'un avion$M$ est le rapport entre sa vitesse et la vitesse du son. Lorsqu'un avion vole à une altitude constante, son angle de Mach est donné par$μ=2\sin^{−1}\left(\frac{1}{M}\right).$

Trouvez l'angle de Mach (au degré le plus proche) pour les nombres de Mach suivants.

1,0 »." style="width: 465px; height: 305px;" width="465px" height="305px" src="https://math.libretexts.org/@api/dek...01_04_215.jpeg">

un.$μ=1.4$

b.$μ=2.8$

c.$μ=4.3$

Réponse: a.$\sim 92°$ b.$\sim 42°$ c.$\sim 27°$

40) [T] À l'aide de$μ=2\sin^{−1}\left(\frac{1}{M}\right)$, trouvez le nombre de Mach M pour les angles suivants.

un.$μ=\frac{π}{6}$

b.$μ=\frac{2π}{7}$

c.$μ=\frac{3π}{8}$

41) [T] La température (en degrés Celsius) d'une ville du nord des États-Unis peut être modélisée par la fonction

$T(x)=5+18\sin\left[\frac{π}{6}(x−4.6)\right],$

où$x$ est le temps en mois et$x=1.00$ correspond au 1er janvier. Déterminez le mois et le jour où la température est$21°C.$

Réponse: $x≈6.69,\, 8.51$; donc, la température se produit le 21 juin et le 15 août

42) [T] La profondeur (en pieds) de l'eau sur un quai varie en fonction de la montée et de la descente des marées. Il est modélisé par la fonction$D(t)=5\sin\left(\frac{π}{6}t−\frac{7π}{6}\right)+8,$ où$t$ est le nombre d'heures après minuit. Déterminez la première fois après minuit lorsque la profondeur est de$11.75$ pieds.

43) [T] Un objet se déplaçant selon un mouvement harmonique simple est modélisé par la fonction$s(t)=−6\cos\left(\dfrac{πt}{2}\right),$ où$s$ est mesuré en pouces et$t$ mesuré en secondes. Déterminez la première fois que la distance parcourue est$4.5$ atteinte.

Réponse: $\sim 1.5$seconde

44) [T] Une galerie d'art locale possède un portrait de 3 pieds de haut accroché à 2,5 pieds au-dessus du niveau des yeux d'une personne moyenne. L'angle de vision$θ$ peut être modélisé par la fonction$θ=\tan^{−1}\frac{5.5}{x}−\tan^{−1}\frac{2.5}{x}$, où$x$ est la distance (en pieds) par rapport au portrait. Trouvez l'angle de vision lorsqu'une personne se trouve à 4 pieds du portrait.

45) [T] Utilisez une calculatrice pour évaluer$\tan^{−1}(\tan(2.1))$ et$\cos^{−1}(\cos(2.1))$. Expliquez les résultats de chacun.

Réponse: $\tan^{−1}(\tan(2.1))≈−1.0416$; l'expression n'est pas égale$2.1$ puisque$2.1>1.57=\frac{π}{2}$, en d'autres termes, elle n'appartient pas au domaine restreint de$\tan x$. $\cos^{−1}(\cos(2.1))=2.1$, puisqu'$2.1$il appartient au domaine restreint de$\cos x$.

46) [T] Utilisez une calculatrice pour évaluer$\sin(\sin^{−1}(−2))$ et$\tan(\tan^{−1}(−2))$. Expliquez les résultats de chacun.

Contributeurs

Template:ContribOpenStaxCalc