1.4 : Fonctions inverses
- Page ID
- 197973
- Déterminez les conditions dans lesquelles une fonction possède une inverse.
- Utilisez le test de la ligne horizontale pour savoir quand une fonction est biunivoque.
- Détermine l'inverse d'une fonction donnée.
- Tracez le graphe d'une fonction inverse.
- Évaluez les fonctions trigonométriques inverses.
Une fonction inverse inverse l'opération effectuée par une fonction particulière. En d'autres termes, quoi que fasse une fonction, la fonction inverse l'annule. Dans cette section, nous définissons formellement une fonction inverse et indiquons les conditions nécessaires à l'existence d'une fonction inverse. Nous examinons comment trouver une fonction inverse et étudions la relation entre le graphe d'une fonction et le graphe de son inverse. Nous appliquons ensuite ces idées pour définir et discuter des propriétés des fonctions trigonométriques inverses.
Existence d'une fonction inverse
Nous commençons par un exemple. À partir d'une fonction\(f\) et d'une sortie\(y=f(x)\), nous cherchons souvent à déterminer la ou les valeurs\(y\) par lesquelles la ou les valeurs\(x\) ont été mappées\(f\). Par exemple, considérez la fonction\(f(x)=x^3+4\). Depuis toute sortie\(y=x^3+4\), nous pouvons résoudre cette équation\(x\) pour trouver que l'entrée est\(x=\sqrt[3]{y−4}\). Cette équation se définit\(x\) comme une fonction de\(y\). En désignant cette fonction comme\(f^{−1}\), et en écrivant\(x=f^{−1}(y)=\sqrt[3]{y−4}\), nous voyons que pour tout ce qui\(x\) se trouve dans le domaine de\(f,f^{−1}\)\(f(x))=f^{−1}(x^3+4)=x\). Ainsi, cette nouvelle fonction a « annulé » ce que faisait la fonction\(f\) d'origine.\(f^{−1}\) Une fonction dotée de cette propriété est appelée fonction inverse de la fonction d'origine.
Étant donné une fonction\(f\) avec domaine\(D\) et plage\(R\), sa fonction inverse (si elle existe) est la fonction\(f^{−1}\) avec domaine\(R\) et plage\(D\) telle que\(f^{−1}(y)=x\) if et only if\(f(x)=y\). En d'autres termes, pour une fonction\(f\) et son inverse\(f^{−1}\),
\[f^{−1}(f(x))=x \nonumber \]
pour tous\(x\)\(D\)
\[f(f^{−1}(y))=y \nonumber \]
pour tous\(y\)\(R\).
Notez que cela\(f^{−1}\) se lit comme «\(f\) inverse ». Ici, le n'\(−1\)est pas utilisé comme exposant, donc
\[f^{−1}(x)≠ \dfrac{1}{f(x)}. \nonumber \]
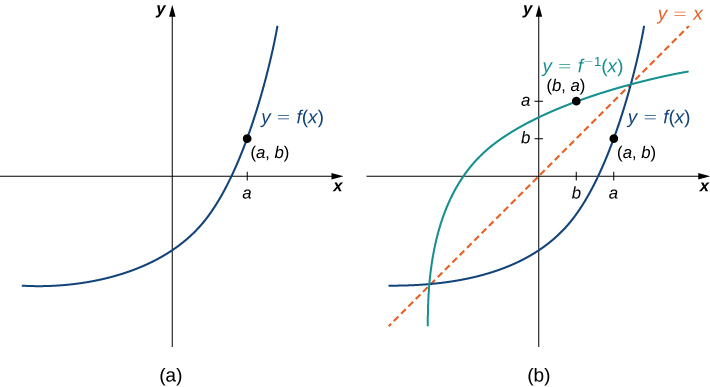
La figure\(\PageIndex{1}\) montre la relation entre le domaine et la plage de\(f\) et le domaine et la plage de\(f^{−1}\).
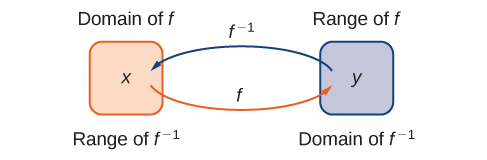
Rappelez-vous qu'une fonction possède exactement une sortie pour chaque entrée. Par conséquent, pour définir une fonction inverse, nous devons mapper chaque entrée sur exactement une sortie. Par exemple, essayons de trouver la fonction inverse pour\(f(x)=x^2\). En résolvant l'équation\(y=x^2\) pour\(x\), nous arrivons à l'équation\(x=±\sqrt{y}\). Cette équation ne se décrit pas en fonction de\(x\)\(y\) car il existe deux solutions à cette équation pour chacune d'entre elles\(y>0\). Le problème lorsque vous essayez de trouver une fonction inverse pour\(f(x)=x^2\) est que deux entrées sont envoyées à la même sortie pour chaque sortie\(y>0\). La fonction\(f(x)=x^3+4\) évoquée précédemment ne présentait pas ce problème. Pour cette fonction, chaque entrée était envoyée vers une sortie différente. Une fonction qui envoie chaque entrée vers une sortie différente est appelée fonction biunivoque.
Nous disons qu'une fonction\(f\) est une fonction biunivoque si\(f(x_1)≠f(x_2)\) quand\(x_1≠x_2\).
L'un des moyens de déterminer si une fonction est biunivoque consiste à regarder son graphique. Si une fonction est biunivoque, aucune entrée ne peut être envoyée vers la même sortie. Par conséquent, si nous dessinons une ligne horizontale n'importe où dans le\(xy\) plan, selon le test de la ligne horizontale, elle ne peut pas intersecter le graphique plus d'une fois. Nous remarquons que le test de la ligne horizontale est différent du test de la ligne verticale. Le test de la ligne verticale permet de déterminer si un graphe est le graphe d'une fonction. Le test de la ligne horizontale permet de déterminer si une fonction est biunivoque (Figure\(\PageIndex{2}\)).
Une fonction\(f\) est biunivoque si et seulement si chaque ligne horizontale ne coupe\(f\) pas plus d'une fois le graphe.
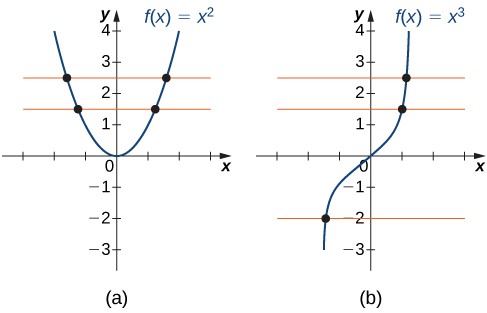
Pour chacune des fonctions suivantes, utilisez le test de la ligne horizontale pour déterminer s'il s'agit d'une fonction biunivoque.
a)
b)
Solution
a) Comme la ligne horizontale\(y=n\) d'un entier\(n≥0\) coupe le graphe plus d'une fois, cette fonction n'est pas biunivoque.
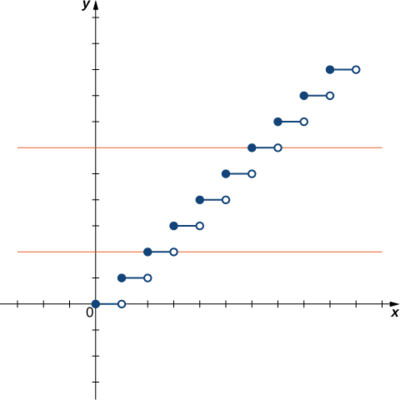
b) Comme chaque ligne horizontale coupe le graphique une seule fois (au plus), cette fonction est biunivoque.
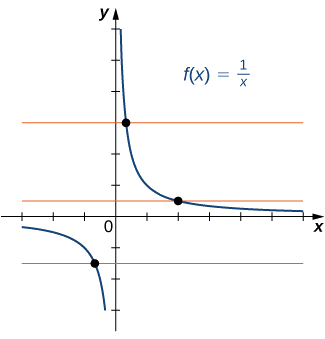
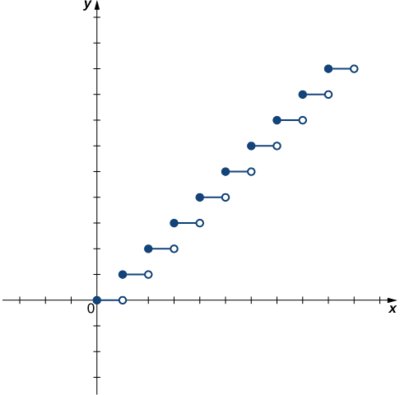
La fonction est-elle\(f\) représentée graphiquement dans l'image suivante une à une ?
- Solution
-
Utilisez le test de la ligne horizontale.
- Réponse
-
Non
Trouver l'inverse d'une fonction
Nous pouvons maintenant examiner les fonctions individuelles et montrer comment trouver leurs inverses. Rappelons qu'une fonction mappe des éléments du domaine de\(f\) à des éléments compris dans la plage de\(f\). La fonction inverse mappe chaque élément de la plage de\(f\) retour à son élément correspondant dans le domaine de\(f\). Par conséquent, pour trouver la fonction inverse d'une fonction biunivoque\(f\), étant donnée une valeur comprise\(y\) dans la plage de\(f\), nous devons déterminer laquelle\(f\) satisfait\(x\) dans le domaine des\(f(x)=y\). Puisque\(f\) c'est un pour un, il existe exactement une telle valeur\(x\). Nous pouvons trouver cette valeur\(x\) en résolvant l'équation\(f(x)=y\) de\(x\). Ce faisant, nous pouvons écrire\(x\) en fonction de l'\(y\)endroit où le domaine de cette fonction est la plage de\(f\) et où la plage de cette nouvelle fonction est le domaine de\(f\). Par conséquent, cette fonction est l'inverse de\(f\), et nous écrivons\(x=f^{−1}(y)\). Comme nous utilisons généralement la variable\(x\) pour désigner la variable indépendante et y pour désigner la variable dépendante, nous interchangeons souvent les rôles de\(x\) et et\(y\) d'écriture\(y=f^{−1}(x)\). Représenter la fonction inverse de cette manière est également utile plus tard lorsque nous tracons une fonction\(f\) et son inverse\(f^{−1}\) sur les mêmes axes.
- Résolvez l'équation\(y=f(x)\) pour\(x\).
- Échangez les variables\(x\)\(y\) et écrivez\(y=f^{−1}(x)\).
Trouvez l'inverse de la fonction\(f(x)=3x−4.\) State the domain and range de la fonction inverse. Vérifiez que\(f^{−1}(f(x))=x.\)
Solution
Suivez les étapes décrites dans la stratégie.
Étape 1. Si\(y=3x−4,\) alors\(3x=y+4\) et\(x=\frac{1}{3}y+\frac{4}{3}.\)
Étape 2. Réécrivez comme\(y=\frac{1}{3}x+\frac{4}{3}\) et laissez.\(y=f^{−1}(x)\) Par conséquent,\(f^{−1}(x)=\frac{1}{3}x+\frac{4}{3}\).
Puisque le domaine de\(f\) est\((−∞,∞)\), la gamme de\(f^{−1}\) est\((−∞,∞)\). Puisque la gamme de\(f\) est\((−∞,∞)\), le domaine de\(f^{−1}\) est\((−∞,∞)\).
Vous pouvez le vérifier\(f^{−1}(f(x))=x\) en écrivant
\(f^{−1}(f(x))=f^{−1}(3x−4)=\frac{1}{3}(3x−4)+\frac{4}{3}=x−\frac{4}{3}+\frac{4}{3}=x.\)
Notez que\(f^{−1}(x)\) pour être l'inverse de\(f(x)\), à la fois\(f^{−1}(f(x))=x\) et\(f(f^{−1}(x))=x\) pour tous\(x\) dans le domaine de la fonction interne.
Détermine l'inverse de la fonction\(f(x)=3x/(x−2)\). Indiquez le domaine et la plage de la fonction inverse.
- Allusion
-
Utilisez la stratégie de résolution de problèmes pour trouver des fonctions inverses.
- Réponse
-
\(f^{−1}(x)=\dfrac{2x}{x−3}\). Le domaine de\(f^{−1}\) est\(\{x\,|\,x≠3\}\). La gamme de\(f^{−1}\) est\(\{y\,|\,y≠2\}\).
Représentation graphique de fonctions inverses
Examinons la relation entre le graphe d'une fonction\(f\) et le graphe de son inverse. Considérez le graphique de la\(f\) figure\(\PageIndex{3}\) et un point\((a,b)\) sur le graphique. Depuis\(b=f(a)\), alors\(f^{−1}(b)=a\). Par conséquent, lorsque nous établissons un graphique\(f^{−1}\), le point\((b,a)\) se trouve sur le graphique. Par conséquent, le graphe de\(f^{−1}\) est le reflet du graphe d'\(f\)environ la ligne\(y=x\).
Pour le graphique de\(f\) l'image suivante, esquissez un graphique\(f^{−1}\) en esquissant la ligne\(y=x\) et en utilisant la symétrie. Identifiez le domaine et la gamme de\(f^{−1}\).
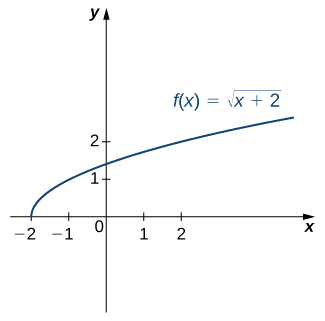
Solution
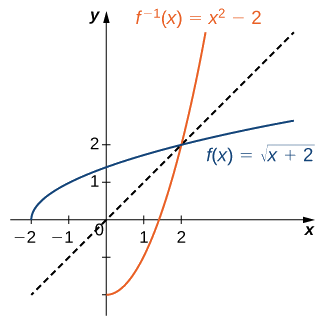
Reflète le graphique autour de la ligne\(y=x\). Le domaine de\(f^{−1}\) est\([0,∞)\). La gamme de\(f^{−1}\) est\([−2,∞)\). En utilisant la stratégie précédente pour trouver des fonctions inverses, nous pouvons vérifier que la fonction inverse est\(f^{−1}(x)=x^2−2\), comme indiqué sur le graphique.
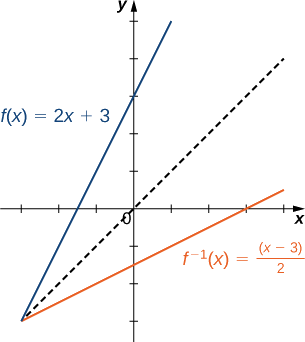
Esquissez le graphe\(f(x)=2x+3\) et le graphe de son inverse à l'aide de la propriété de symétrie des fonctions inverses.
- Allusion
-
Les graphes sont symétriques par rapport à la ligne\(y=x\)
- Réponse
-
Limiter les domaines
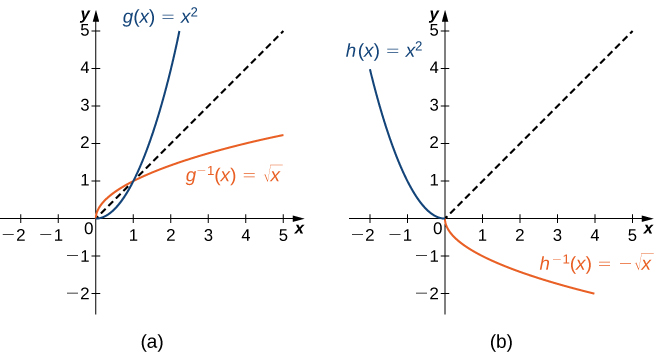
Comme nous l'avons vu,\(f(x)=x^2\) n'a pas de fonction inverse car elle n'est pas biunivoque. Cependant, nous pouvons choisir un sous-ensemble du domaine de\(f\) telle sorte que la fonction soit biunivoque. Ce sous-ensemble est appelé domaine restreint. En restreignant le domaine de\(f\), nous pouvons définir une nouvelle fonction de\(g\) telle sorte que le domaine de\(g\) soit le domaine restreint de\(f\) et\(g(x)=f(x)\) pour tous\(x\) dans le domaine de\(g\). Ensuite, nous pouvons définir une fonction inverse pour\(g\) ce domaine. Par exemple, comme\(f(x)=x^2\) il s'agit d'un à un sur l'intervalle\([0,∞)\), nous pouvons définir une nouvelle fonction de\(g\) telle sorte que le domaine de\(g\) est\([0,∞)\) et\(g(x)=x^2\) pour tous\(x\) dans son domaine. Comme il\(g\) s'agit d'une fonction biunivoque, elle a une fonction inverse, donnée par la formule\(g^{−1}(x)=\sqrt{x}\). D'autre part, la fonction\(f(x)=x^2\) est également individuelle sur le domaine\((−∞,0]\). Par conséquent, nous pourrions également définir une nouvelle fonction\(h\) telle que le domaine de\(h\) est\((−∞,0]\) et\(h(x)=x^2\) pour tous\(x\) dans le domaine de\(h\). \(h\)Il s'agit alors d'une fonction biunivoque qui doit également avoir une inverse. Son inverse est donné par la formule\(h^{−1}(x)=−\sqrt{x}\) (Figure\(\PageIndex{4}\)).
Réfléchissez à la fonction\(f(x)=(x+1)^2\).
- Esquissez le graphique\(f\) et utilisez le test de la ligne horizontale pour montrer qu'il ne\(f\) s'agit pas d'un à un.
- Afficher que\(f\) c'est un à un sur le domaine restreint\([−1,∞)\). Déterminez le domaine et la plage pour l'inverse de\(f\) sur ce domaine restreint et trouvez une formule pour\(f^{−1}\).
Solution
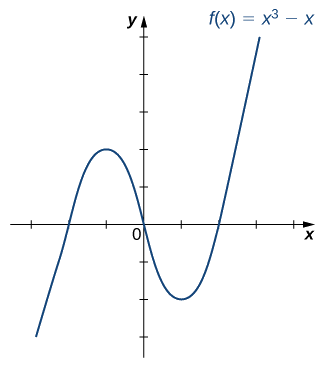
a) Le graphique de\(f\) est le graphique de l'\(1\)unité gauche\(y=x^2\) décalée. Comme il existe une ligne horizontale coupant le graphique plus d'une fois, elle n'\(f\)est pas biunivoque.
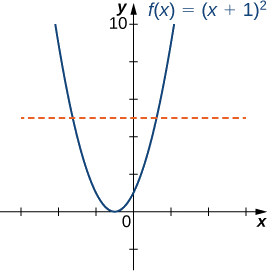
b) L'intervalle\([−1,∞),\;f\) est un pour un.
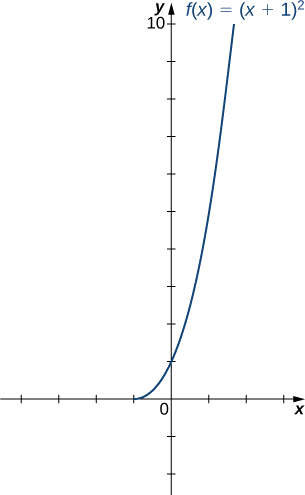
Le domaine et la plage de\(f^{−1}\) sont donnés par la plage et le domaine de\(f\), respectivement. Par conséquent, le domaine de\(f^{−1}\) est\([0,∞)\) et la gamme de\(f^{−1}\) est\([−1,∞)\). Pour trouver une formule pour\(f^{−1}\), résolvez l'équation\(y=(x+1)^2\) de\(x.\) If\(y=(x+1)^2\), alors\(x=−1±\sqrt{y}\). Puisque nous limitons le domaine à l'intervalle où nous\(x≥−1\) en avons besoin\(±\sqrt{y}≥0\). Par conséquent,\(x=−1+\sqrt{y}\). En échangeant\(x\) et\(y\), nous écrivons\(y=−1+\sqrt{x}\) et concluons que\(f^{−1}(x)=−1+\sqrt{x}\).
Envisagez de vous\(f(x)=1/x^2\) limiter au domaine\((−∞,0)\). Vérifiez qu'il\(f\) s'agit d'une réponse individuelle sur ce domaine. Déterminez le domaine et la plage de l'inverse de\(f\) et trouvez une formule pour\(f^{−1}\).
- Allusion
-
Le domaine et la plage de\(f^{−1}\) sont donnés par la plage et le domaine de\(f\), respectivement. Pour trouver\(f^{−1}\), résoudre\(y=1/x^2\) pour\(x\).
- Réponse
-
Le domaine de\(f^{−1}\) est\((0,∞)\). La gamme de\(f^{−1}\) est\((−∞,0)\). La fonction inverse est donnée par la formule\(f^{−1}(x)=−1/\sqrt{x}\).
Fonctions trigonométriques inverses
Les six fonctions trigonométriques de base sont périodiques et ne sont donc pas univoques. Cependant, si nous limitons le domaine d'une fonction trigonométrique à un intervalle où elle est biunivoque, nous pouvons définir son inverse. Considérez la fonction sinusoïdale. La fonction sinus est biunivoque sur un nombre infini d'intervalles, mais la convention standard est de limiter le domaine à l'intervalle\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Ce faisant, nous définissons la fonction sinusoïdale inverse sur le domaine de\([−1,1]\) telle sorte que pour n'importe quel\(x\) angle de l'intervalle\([−1,1]\), la fonction sinusoïdale inverse nous indique quel angle\(θ\) de l'intervalle\(\left[−\frac{π}{2},\frac{π}{2}\right]\) satisfait\(\sin θ=x\). De même, nous pouvons restreindre les domaines des autres fonctions trigonométriques pour définir des fonctions trigonométriques inverses, qui sont des fonctions qui nous indiquent quel angle dans un certain intervalle possède une valeur trigonométrique spécifiée.
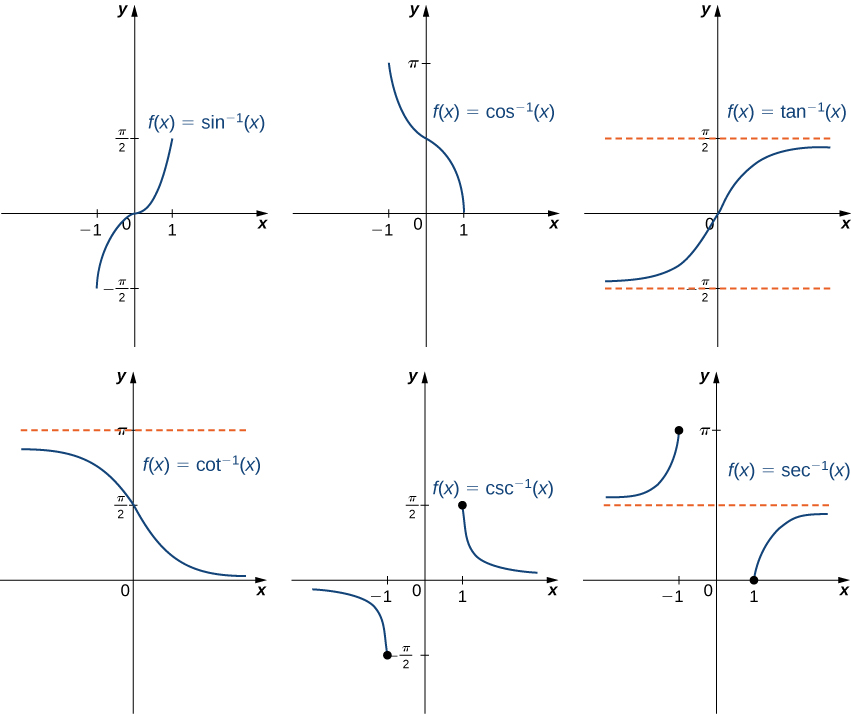
La fonction sinusoïdale inverse, notée\(\sin^{−1}\) ou\(\arcsin\), et la fonction cosinus inverse, notée\(\cos^{−1}\) ou\(\arccos\), sont définies sur le domaine\(D=\{x|−1≤x≤1\}\) comme suit :
\(\sin^{−1}(x)=y\)
- si et seulement si et seulement si\(\sin(y)=x\) et\(−\frac{π}{2}≤y≤\frac{π}{2}\) ;
\(\cos^{−1}(x)=y\)
- si et seulement si\(\cos(y)=x\) et\(0≤y≤π\).
La fonction tangente inverse, notée\(\tan^{−1}\) ou\(\arctan\), et la fonction cotangente inverse, notée\(\cot^{−1}\) ou\(\operatorname{arccot}\), sont définies sur le domaine\(D=\{x|−∞<x<∞\}\) comme suit :
\(\tan^{−1}(x)=y\)
- si et seulement si et seulement si\(\tan(y)=x\) et\(−\frac{π}{2}<y<\frac{π}{2}\) ;
\(\cot^{−1}(x)=y\)
- si et seulement si\(\cot(y)=x\) et\(0<y<π\).
La fonction cosécante inverse, notée\(\csc^{−1}\) ou\(\operatorname{arccsc}\), et la fonction sécante inverse, notée\(\sec^{−1}\) ou\(\operatorname{arcsec}\), sont définies dans le domaine\(D=\{x\,|\,|x|≥1\}\) comme suit :
\(\csc^{−1}(x)=y\)
- si et seulement si et seulement si\(\csc(y)=x\) et\(−\frac{π}{2}≤y≤\frac{π}{2}, \, y≠0\) ;
\(\sec^{−1}(x)=y\)
- si et seulement si\(\sec(y)=x\) et\(0≤y≤π, \, y≠π/2\).
Pour représenter graphiquement les fonctions trigonométriques inverses, nous utilisons les graphes des fonctions trigonométriques restreints aux domaines définis précédemment et reflétons les graphes concernant la ligne\(y=x\) (Figure\(\PageIndex{5}\)).
Lors de l'évaluation d'une fonction trigonométrique inverse, la sortie est un angle. Par exemple, pour évaluer\(\cos^{−1}\left(\frac{1}{2}\right)\), nous devons trouver un angle\(θ\) tel que\(\cos θ=\frac{1}{2}\). De toute évidence, de nombreux angles possèdent cette propriété. Cependant, étant donné la définition de\(\cos^{−1}\), nous avons besoin de l'angle\(θ\) qui non seulement résout cette équation, mais se situe également dans l'intervalle\([0,π]\). Nous en concluons que\(\cos^{−1}\left(\frac{1}{2}\right)=\frac{π}{3}\).
Nous examinons maintenant la composition d'une fonction trigonométrique et son inverse. Par exemple, considérez les deux expressions\(\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\) et\(\sin^{−1}(\sin(π)).\)
Pour le premier, nous simplifions comme suit :
\[\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)=\sin\left(\frac{π}{4}\right)=\frac{\sqrt{2}}{2}.\nonumber \]
Pour le second, nous avons
\[\sin^{−1}(\sin(π))=\sin^{−1}(0)=0.\nonumber \]
La fonction inverse est censée « annuler » la fonction d'origine, alors pourquoi ne pas\(\sin^{−1}(\sin(π))=π?\), si l'on se souvient de notre définition des fonctions inverses, une fonction\(f\) et son inverse\(f^{−1}\) remplissent les conditions\(f(f^{−1}(y))=y\) pour tous\(y\) dans le domaine de\(f^{−1}\) et\(f^{−1}(f(x))=x\) pour tous\(x\) le domaine de\(f\), alors que s'est-il passé ici ? Le problème est que la fonction sinusoïdale inverse\(\sin^{−1}\), est l'inverse de la fonction sinusoïdale restreinte définie sur le domaine\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Par conséquent, car\(x\) dans l'intervalle\([−\frac{π}{2},\frac{π}{2}]\), il est vrai que\(\sin^{−1}(\sin x)=x\). Toutefois, pour les valeurs\(x\) situées en dehors de cet intervalle, l'équation ne tient pas, même si elle\(\sin^{−1}(\sin x)\) est définie pour tous les nombres réels\(x\).
Qu'en\(\sin(\sin^{−1}y)?\) est-il de cela a un problème similaire ? La réponse est non. Puisque le domaine de\(\sin^{−1}\) est l'intervalle\([−1,1]\), nous concluons que\(\sin\left(\sin^{−1}y\right)=y\) si\(−1≤y≤1\) et l'expression n'est pas définie pour les autres valeurs de\(y\). Pour résumer,
\(\sin(\sin^{−1}y)=y\)si\(−1≤y≤1\)
et
\(\sin^{−1}(\sin x)=x\)si\(−\frac{π}{2}≤x≤\frac{π}{2}.\)
De même, pour la fonction cosinus,
\(\cos(\cos^{−1}y)=y\)si\(−1≤y≤1\)
et
\(\cos^{−1}(\cos x)=x\)si\(0≤x≤π.\)
Des propriétés similaires s'appliquent aux autres fonctions trigonométriques f et à leurs inverses.
Évaluez chacune des expressions suivantes.
- \(\sin^{−1}\left(−\frac{\sqrt{3}}{2}\right)\)
- \(\tan\left(\tan^{−1}\left(−\frac{1}{\sqrt{3}}\right)\right)\)
- \(\cos^{−1}\left(\cos\left(\frac{5π}{4}\right)\right)\)
- \(\sin^{−1}\left(\cos\left(\frac{2π}{3}\right)\right)\)
Solution
- L'évaluation\(\sin^{−1}(−\sqrt{3}/2)\) équivaut à trouver l'angle\(θ\) tel que\(\sin θ=−\sqrt{3}/2\) et\(−π/2≤θ≤π/2\). L'angle\(θ=−π/3\) répond à ces deux conditions. Par conséquent,\(\sin^{−1}(−\sqrt{3}/2)=−π/3\).
- Nous utilisons d'abord le fait que\(\tan^{−1}(−1/\sqrt{3})=−π/6.\) Then\(\tan(-π/6)=−1/\sqrt{3}\). Par conséquent,\(\tan(\tan^{−1}(−1/\sqrt{3}))=−1/\sqrt{3}\).
- Pour évaluer\(\cos^{−1}(\cos(5π/4))\), utilisez d'abord le fait que\(\cos(5π/4)=−\sqrt{2}/2\). Ensuite, nous devons trouver l'angle\(θ\) tel que\(\cos(θ)=−\sqrt{2}/2\) et\(0≤θ≤π\). Puisque\(3π/4\) répond à ces deux conditions, nous avons\(\cos^{-1}(\cos(5π/4))=\cos^{−1}(−\sqrt{2}/2))=3π/4\).
- Depuis\(\cos(2π/3)=−1/2\), nous devons évaluer\(\sin^{−1}(−1/2)\). C'est-à-dire que nous devons trouver l'angle\(θ\) tel que\(\sin(θ)=−1/2\) et\(−π/2≤θ≤π/2\). Étant donné\(−π/6\) que ces deux conditions sont réunies, nous pouvons en conclure que\(\sin^{−1}(\cos(2π/3))=\sin^{−1}(−1/2)=−π/6.\)
Dans de nombreux domaines des sciences, de l'ingénierie et des mathématiques, il est utile de connaître la valeur maximale qu'une fonction peut obtenir, même si nous ne connaissons pas sa valeur exacte à un instant donné. Par exemple, si nous avons une fonction décrivant la résistance d'une poutre de toit, nous aimerions connaître le poids maximum que la poutre peut supporter sans se casser. Si nous avons une fonction qui décrit la vitesse d'un train, nous aimerions connaître sa vitesse maximale avant qu'il ne saute des rails. La sécurité de la conception dépend souvent de la connaissance des valeurs maximales.
Ce projet décrit un exemple simple de fonction dont la valeur maximale dépend de deux coefficients d'équation. Nous verrons que les valeurs maximales peuvent dépendre de plusieurs facteurs autres que la variable indépendante\(x\).
1. Examinez le graphique de la figure\(\PageIndex{6}\) de la fonction\(y=\sin x+\cos x.\) Décrivez sa forme générale. Est-ce périodique ? Comment le sais-tu ?
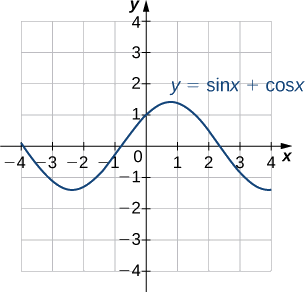
À l'aide d'une calculatrice graphique ou d'un autre appareil graphique, estimez les\(y\) valeurs\(x\) - et - du point maximum du graphique (le premier point de ce type où\(x > 0\)). Il peut être utile d'exprimer la\(x\) valeur -comme un multiple de\(π.\)
2. Examinez maintenant d'autres graphes du formulaire\(y=A\sin x+B\cos x\) pour différentes valeurs de\(A\) et\(B.\) esquissez le graphique quand\(A = 2\)\(B = 1,\) et trouvez les\(y\) valeurs\(x\) - et - pour le point maximum. (N'oubliez pas d'exprimer la\(x\) valeur -sous la forme d'un multiple de\(π\), si possible.) Est-ce qu'il a déménagé ?
3. Répétez pour\(A = 1, \,B = 2.\) Y a-t-il un lien avec ce que vous avez trouvé dans la partie (2) ?
4. Complétez le tableau suivant en ajoutant quelques choix de votre choix pour\(A\) et\(B:\)
| \(A\) | \(B\) | \(x\) | \(y\) | \(A\) | \(B\) | \(x\) | \(y\) |
|---|---|---|---|---|---|---|---|
| \ (A \) » style="vertical-align:middle ; « >0 | \ (B \) » style="vertical-align:middle ; « >1 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > | \ (A \) » style="vertical-align:middle ; « >3 | \ (B \) » style="vertical-align:middle ; « >4 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > |
| \ (A \) » style="vertical-align:middle ; ">1 | \ (B \) » style="vertical-align:middle ; « >0 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > | \ (A \) » style="vertical-align:middle ; « >4 | \ (B \) » style="vertical-align:middle ; « >3 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > |
| \ (A \) » style="vertical-align:middle ; ">1 | \ (B \) » style="vertical-align:middle ; « >1 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > | \ (A \) » style="vertical-align:middle ; « >\(\sqrt{3}\) | \ (B \) » style="vertical-align:middle ; « >1 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > |
| \ (A \) » style="vertical-align:middle ; ">1 | \ (B \) » style="vertical-align:middle ; « >2 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > | \ (A \) » style="vertical-align:middle ; ">1 | \ (B \) » style="vertical-align:middle ; « >\(\sqrt{3}\) | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > |
| \ (A \) » style="vertical-align:middle ; ">2 | \ (B \) » style="vertical-align:middle ; « >1 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > | \ (A \) » style="vertical-align:middle ; « >12 | \ (B \) » style="vertical-align:middle ; « >5 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > |
| \ (A \) » style="vertical-align:middle ; ">2 | \ (B \) » style="vertical-align:middle ; « >2 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > | \ (A \) » style="vertical-align:middle ; « >5 | \ (B \) » style="vertical-align:middle ; « >12 | \ (x \) » style="vertical-align:middle ; « > | \ (y \) » style="vertical-align:middle ; « > |
5. Essayez de trouver la formule pour les\(y\) valeurs.
6. La formule pour les\(x\) valeurs -est un peu plus complexe. Les points les plus utiles du tableau sont\((1,1),\, (1,\sqrt{3}),\, (\sqrt{3},1).\) (Conseil : considérez les fonctions trigonométriques inverses.)
7. Si vous avez trouvé des formules pour les parties (5) et (6), montrez qu'elles fonctionnent ensemble. En d'autres termes, remplacez la formule\(x\) -value dans laquelle vous vous\(y=A\sin x+B\cos x\) trouvez et simplifiez-la pour obtenir la formule\(y\) -value que vous avez trouvée.
Concepts clés
- Pour qu'une fonction ait une inverse, elle doit être biunivoque. À partir du graphe d'une fonction, nous pouvons déterminer si la fonction est biunivoque en utilisant le test de la ligne horizontale.
- Si une fonction n'est pas biunivoque, nous pouvons restreindre le domaine à un domaine plus petit où la fonction est biunivoque, puis définir l'inverse de la fonction sur le plus petit domaine.
- Pour une fonction\(f\) et son inverse\(f^{−1},\, f(f^{−1}(x))=x\) pour tous\(x\) dans le domaine de\(f^{−1}\) et\(f^{−1}(f(x))=x\) pour tous\(x\) dans le domaine de\(f\).
- Les fonctions trigonométriques étant périodiques, nous devons restreindre leurs domaines pour définir les fonctions trigonométriques inverses.
- Le graphe d'une fonction\(f\) et son inverse\(f^{−1}\) sont symétriques par rapport à la droite\(y=x.\)
Équations clés
- Fonction inverse
\(f^{−1}(f(x))=x\)pour tous\(x\)\(D,\) et\(f(f^{−1}(y))=y\) pour tous\(y\)\(R\).
Lexique
- test de ligne horizontale
- une fonction\(f\) est biunivoque si et seulement si chaque ligne horizontale coupe le graphe\(f\) d'au plus une fois
- fonction inverse
- pour une fonction\(f\), la fonction inverse\(f^{−1}\) satisfait\(f^{−1}(y)=x\) si\(f(x)=y\)
- fonctions trigonométriques inverses
- les inverses des fonctions trigonométriques sont définis sur des domaines restreints où il s'agit de fonctions biunivoques
- fonction un à un
- une fonction\(f\) est biunivoque\(f(x_1)≠f(x_2)\) si\(x_1≠x_2\)
- domaine restreint
- un sous-ensemble du domaine d'une fonction\(f\)


