1.3E : Exercices pour la section 1.3

Last updated
Save as PDF

Page ID: 198008

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 5, convertissez chaque angle en degrés en radians. Écrivez la réponse sous la forme d'un multiple de$π$.

1)$240°$

Réponse: $\frac{4π}{3}$rad

2)$15°$

3)$60°$

Réponse: $\frac{π}{3}$rad

4)$-225°$

5)$330°$

Réponse: $\frac{11π}{6}$rad

Dans les exercices 6 à 10, convertissez chaque angle en radians en degrés.

6)$\frac{π}{2}$ Lire

7)$\frac{7π}{6}$ Lire

Réponse: $210°$

8)$\frac{11π}{2}$ lire

(9)$-3π$ lire

Réponse: $-540°$

(10)$\frac{5π}{12}$ lire

Dans les exercices 11 à 16, évaluez les valeurs fonctionnelles.

11)$\cos \frac{4π}{3}$

Réponse: $\cos \frac{4π}{3}=-0.5$

(12)$\tan \frac{19π}{4}$

13)$\sin \left(-\frac{3π}{4}\right)$

Réponse: $\sin \left(-\frac{3π}{4}\right) = -\frac{\sqrt{2}}{2}$

(14)$\sec \left(-\frac{π}{6}\right)$

15)$\sin \left(-\frac{π}{12}\right)$

Réponse: $\sin \left(-\frac{π}{12}\right) = \dfrac{\sqrt{3}-1}{2\sqrt{2}}$

16)$\cos \left(-\frac{5π}{12}\right)$

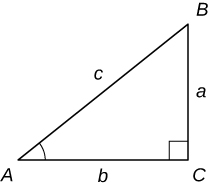
Dans les exercices 17 à 22, considérez le triangle comme$ABC,$ un triangle droit avec un angle droit à$C.$

a. Trouvez le côté manquant du triangle.

b. Trouvez les six valeurs de la fonction trigonométrique pour l'angle à$A.$

Si nécessaire, arrondissez à la première décimale.

$Image d'un triangle. Les trois coins du triangle sont étiquetés « A », « B » et « C ». Entre le coin A et le coin C se trouve le côté b. Entre le coin C et le coin B se trouve le côté a. Entre le coin B et le coin A se trouve le côté c. L'angle du coin C est indiqué par un symbole de triangle droit. L'angle du coin A est indiqué par un symbole d'angle.$ 225 ° = 225 ° ⋅ π 180 ° = 5 π 4

17)

Template:ContribOpenStaxCalc