1.3 : Fonctions trigonométriques
- Page ID
- 197995
- Convertissez les mesures d'angle en degrés et en radians.
- Reconnaître les définitions triangulaires et circulaires des fonctions trigonométriques de base.
- Écrivez les identités trigonométriques de base.
- Identifier les graphes et les périodes des fonctions trigonométriques.
- Décrivez le décalage d'un graphe en sinus ou en cosinus par rapport à l'équation de la fonction.
Les fonctions trigonométriques sont utilisées pour modéliser de nombreux phénomènes, notamment les ondes sonores, les vibrations des cordes, le courant électrique alternatif et le mouvement des pendules. En fait, presque tous les mouvements répétitifs ou cycliques peuvent être modélisés par une combinaison de fonctions trigonométriques. Dans cette section, nous définissons les six fonctions trigonométriques de base et examinons certaines des principales identités impliquant ces fonctions.
Mesure du rayonnement
Pour utiliser les fonctions trigonométriques, il faut d'abord comprendre comment mesurer les angles. Bien que nous puissions utiliser à la fois des radians et des degrés, les radians constituent une mesure plus naturelle car ils sont directement liés au cercle unitaire, un cercle de rayon 1. La mesure en radian d'un angle est définie comme suit. Étant donné un angle\(θ\),\(s\) soit la longueur de l'arc correspondant sur le cercle unitaire (Figure\(\PageIndex{1}\)). Nous disons que l'angle correspondant à l'arc de longueur 1 a une mesure de radian de 1.
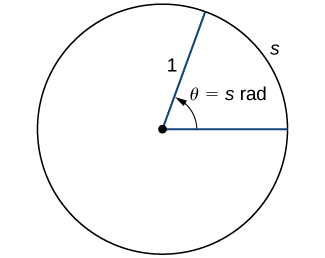
Puisqu'un angle de\(360°\) correspond à la circonférence d'un cercle, ou d'un arc de longueur\(2π\), nous concluons qu'un angle dont la mesure en degrés\(360°\) est de a une mesure en radian de\(2π\). De même, nous voyons que cela\(180°\) équivaut à\(\pi\) des radians. Le tableau\(\PageIndex{1}\) montre la relation entre les valeurs communes en degrés et en radians.
| Diplômes | Radians | Diplômes | Radians |
|---|---|---|---|
| 0 | 0 | 120 | \(2π/3\) |
| 30 | \(π/6\) | 135 | \(3π/4\) |
| 45 | \(π/4\) | 150 | \(5π/6\) |
| 60 | \(π/3\) | 180 | \(π\) |
| 90 | \(π/2\) |
- Express\(225°\) using radians.
- Express\(5π/3\) rad using degrees.
Solution
Utilisez le fait que cela\(180\)° équivaut à\(\pi\) des radians comme facteur de conversion (Tableau\(\PageIndex{1}\)) :
\[1=\dfrac{π \,\mathrm{rad}}{180°}=\dfrac{180°}{π \,\mathrm{rad}}. \nonumber \]
- \(225°=225°⋅\left(\dfrac{π}{180°}\right)=\left(\dfrac{5π}{4}\right)\) rad
- \(\dfrac{5π}{3}\) rad = \(\dfrac{5π}{3}\)⋅\(\dfrac{180°}{π}\)=\(300\)°
- \(210°\)Exprimez en radians.
- Express\(11π/6\) rad using degrees.
- Allusion
-
\(π\)radians est égal à 180°
- Réponse
-
- \(7π/6\)
- 330°
Les six fonctions trigonométriques de base
Les fonctions trigonométriques nous permettent d'utiliser des mesures d'angle, en radians ou en degrés, pour trouver les coordonnées d'un point sur n'importe quel cercle, et pas seulement sur un cercle unitaire, ou pour trouver un angle donné par un point sur un cercle. Ils définissent également la relation entre les côtés et les angles d'un triangle.
Pour définir les fonctions trigonométriques, considérez d'abord le cercle unitaire centré à l'origine et un point\(P=(x,y)\) sur le cercle unitaire. \(θ\)Soit un angle avec un côté initial situé le long de l'\(x\)axe positif et un côté terminal qui est le segment de ligne\(OP\). Un angle dans cette position est considéré comme étant en position standard (Figure\(\PageIndex{2}\)). Nous pouvons ensuite définir les valeurs des six fonctions trigonométriques pour\(θ\) en termes de coordonnées\(x\) et\(y\).
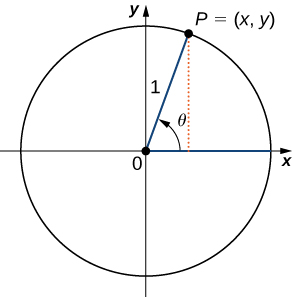
\(P=(x,y)\)Soit un point du cercle unitaire centré à l'origine\(O\). \(θ\)Soit un angle avec un côté initial le long de l'\(x\)axe positif et un côté terminal donné par le segment de ligne\(OP\). Les fonctions trigonométriques sont alors définies comme
| \(\sin θ=y\) | \(\csc θ=\dfrac{1}{y}\) |
| \(\cos θ=x\) | \(\sec θ=\dfrac{1}{x}\) |
| \(\tan θ=\dfrac{y}{x}\) | \(\cot θ=\dfrac{x}{y}\) |
Si\(x=0, \sec θ\) et\(\tan θ\) ne sont pas définis. Si\(y=0\), alors\(\cot θ\) et\(\csc θ\) ne sont pas définis.
Nous pouvons voir que pour un point\(P=(x,y)\) sur un cercle de rayon\(r\) avec un angle correspondant\(θ\), les coordonnées\(x\) et\(y\) satisfont
\[\begin{align} \cos θ &=\dfrac{x}{r} \\ x &=r\cos θ \end{align} \nonumber \]
et
\[\begin{align} \sin θ &=\dfrac{y}{r} \\ y &=r\sin θ. \end{align} \nonumber \]
Les valeurs des autres fonctions trigonométriques peuvent être exprimées en termes de\(x,y\), et\(r\) (Figure\(\PageIndex{3}\)).

Le tableau\(\PageIndex{2}\) montre les valeurs du sinus et du cosinus aux principaux angles du premier quadrant. À partir de ce tableau, nous pouvons déterminer les valeurs du sinus et du cosinus aux angles correspondants dans les autres quadrants. Les valeurs des autres fonctions trigonométriques sont facilement calculées à partir des valeurs de\(\sin θ\) and \(\cos θ.\)
| \(θ\)θ | \(\sin θ\) | \(\cos θ\) |
|---|---|---|
| \ (θ \) θ » style="text-align:center ; « >0 | \ (\ sin θ \) » style="text-align:center ; « >0 | \ (\ cos θ \) » style="text-align:center ; « >1 |
| \ (θ \) θ » style="text-align:center ; « >\(\dfrac{π}{6}\) | \ (\ sin θ \) » style="text-align:center ; « >\(\dfrac{1}{2}\) | \ (\ cos θ \) » style="text-align:center ; « >\(\dfrac{\sqrt{3}}{2}\) |
| \ (θ \) θ » style="text-align:center ; « >\(\dfrac{π}{4}\) | \ (\ sin θ \) » style="text-align:center ; « >\(\dfrac{\sqrt{2}}{2}\) | \ (\ cos θ \) » style="text-align:center ; « >\(\dfrac{\sqrt{2}}{2}\) |
| \ (θ \) θ » style="text-align:center ; « >\(\dfrac{π}{3}\) | \ (\ sin θ \) » style="text-align:center ; « >\(\dfrac{\sqrt{3}}{2}\) | \ (\ cos θ \) » style="text-align:center ; « >\(\dfrac{1}{2}\) |
| \ (θ \) θ » style="text-align:center ; « >\(\dfrac{π}{2}\) | \ (\ sin θ \) » style="text-align:center ; ">1 | \ (\ cos θ \) » style="text-align:center ; « >0 |
Évaluez chacune des expressions suivantes.
- \(\sin \left(\dfrac{2π}{3} \right)\)
- \(\cos \left(−\dfrac{5π}{6} \right)\)
- \(\tan \left(\dfrac{15π}{4}\right)\)
Solution :
a) Sur le cercle unitaire, l'angle\(θ=\dfrac{2π}{3}\) correspond au point\(\left(−\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\). Par conséquent,
\[ \sin \left(\dfrac{2π}{3}\right)=y=\left(\dfrac{\sqrt{3}}{2}\right). \nonumber \]

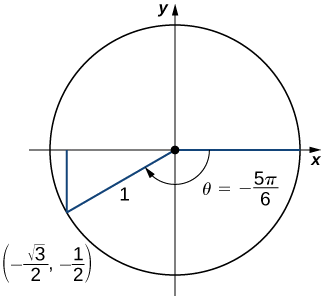
b) Un angle\(θ=−\dfrac{5π}{6}\) corresponds to a revolution in the negative direction, as shown. Therefore,
\[\cos \left(−\dfrac{5π}{6}\right)=x=−\dfrac{\sqrt{3}}{2}. \nonumber \]
c) An angle \(θ\)=\(\dfrac{15π}{4}\)=\(2π\)+\(\dfrac{7π}{4}\). Therefore, this angle corresponds to more than one revolution, as shown. Knowing the fact that an angle of \(\dfrac{7π}{4}\) corresponds to the point \((\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2})\), we can conclude that
\[\tan \left(\dfrac{15π}{4}\right)=\dfrac{y}{x}=−1. \nonumber \]

Evaluate \(\cos(3π/4)\) and \(\sin(−π/6)\).
- Hint
-
Look at angles on the unit circle.
- Answer
-
\[\cos(3π/4) = −\sqrt{2}/2\nonumber \]
\[ \sin(−π/6) =−1/2 \nonumber \]
As mentioned earlier, the ratios of the side lengths of a right triangle can be expressed in terms of the trigonometric functions evaluated at either of the acute angles of the triangle. Let \(θ\) be one of the acute angles. Let \(A\) be the length of the adjacent leg, \(O\) be the length of the opposite leg, and \(H\) be the length of the hypotenuse. By inscribing the triangle into a circle of radius \(H\), as shown in Figure \(\PageIndex{4}\), we see that \(A,H\), and \(O\) satisfy the following relationships with \(θ\):
| \(\sin θ=\dfrac{O}{H}\) | \(\csc θ=\dfrac{H}{O}\) |
| \(\cos θ=\dfrac{A}{H}\) | \(\sec θ=\dfrac{H}{A}\) |
| \(\tan θ=\dfrac{O}{A}\) | \(\cot θ=\dfrac{A}{O}\) |

A wooden ramp is to be built with one end on the ground and the other end at the top of a short staircase. If the top of the staircase is \(4\) ft from the ground and the angle between the ground and the ramp is to be \(10\)°, how long does the ramp need to be?
Solution
Let \(x\) denote the length of the ramp. In the following image, we see that \(x\) needs to satisfy the equation \(\sin(10°)=4/x\). Solving this equation for \(x\), we see that \(x=4/\sin(10°)\)≈\(23.035\) ft.

A house painter wants to lean a \(20\)-ft ladder against a house. If the angle between the base of the ladder and the ground is to be \(60\)°, how far from the house should she place the base of the ladder?
- Hint
-
Draw a right triangle with hypotenuse 20.
- Answer
-
10 ft
Trigonometric Identities
A trigonometric identity is an equation involving trigonometric functions that is true for all angles \(θ\) for which the functions are defined. We can use the identities to help us solve or simplify equations. The main trigonometric identities are listed next.
Reciprocal identities
\[\tan θ=\dfrac{\sin θ}{\cos θ} \nonumber \]
\[\cot θ=\dfrac{\cos θ}{\sin θ} \nonumber \]
\[\csc θ=\dfrac{1}{\sin θ} \nonumber \]
\[\sec θ=\dfrac{1}{\cos θ} \nonumber \]
Pythagorean identities
\[\begin{align} \sin^2θ+\cos^2θ &=1 \label{py1} \\[4pt] 1+\tan^2θ &=\sec^2θ \\[4pt] 1+\cot^2θ &=\csc^2θ \end{align} \]
Addition and subtraction formulas
\[\sin(α±β)=\sin α\cos β±\cos α \sin β \nonumber \]
\[\cos(α±β)=\cos α\cos β∓\sin α \sin β \nonumber \]
Double-angle formulas
\[\sin(2θ)=2\sin θ\cos θ \label{double1} \]
\[\begin{align} \cos(2θ) &=2\cos^2θ−1 \\[4pt] &=1−2\sin^2θ \\[4pt] &=\cos^2θ−\sin^2θ \end{align} \nonumber \]
For each of the following equations, use a trigonometric identity to find all solutions.
- \(1+\cos(2θ)=\cos θ\)
- \(\sin(2θ)=\tan θ\)
Solution
a) Using the double-angle formula for \(\cos(2θ)\), we see that \(θ\) is a solution of
\[1+\cos(2θ)=\cos θ \nonumber \]
if and only if
\[1+2\cos^2θ−1=\cos θ, \nonumber \]
which is true if and only if
\[2\cos^2θ−\cos θ=0. \nonumber \]
To solve this equation, it is important to note that we need to factor the left-hand side and not divide both sides of the equation by \(\cos θ\). The problem with dividing by \(\cos θ\) is that it is possible that \(\cos θ\) is zero. In fact, if we did divide both sides of the equation by \(\cos θ\), we would miss some of the solutions of the original equation. Factoring the left-hand side of the equation, we see that \(θ\) is a solution of this equation if and only if
\[\cos θ(2\cos θ−1)=0. \nonumber \]
Since \(\cos θ=0\) when
\[θ=\dfrac{π}{2},\dfrac{π}{2}±π,\dfrac{π}{2}±2π,…, \nonumber \]
and \(\cos θ=1/2\) when
\[θ=\dfrac{π}{3},\dfrac{π}{3}±2π,…\mathrm{or}\ θ=−\dfrac{π}{3},−\dfrac{π}{3}±2π,…, \nonumber \]
we conclude that the set of solutions to this equation is
\[θ=\dfrac{π}{2}+nπ,\;θ=\dfrac{π}{3}+2nπ \nonumber \]
and
\[θ=−\dfrac{π}{3}+2nπ,\;n=0,±1,±2,….\nonumber \]
b) Using the double-angle formula for \(\sin(2θ)\) and the reciprocal identity for \(\tan(θ)\), the equation can be written as
\[2\sin θ\cos θ=\dfrac{\sin θ}{\cos θ}.\nonumber \]
To solve this equation, we multiply both sides by \(\cos θ\) to eliminate the denominator, and say that if \(θ\) satisfies this equation, then \(θ\) satisfies the equation
\[2\sin θ \cos^2θ−\sin θ=0. \nonumber \]
However, we need to be a little careful here. Even if \(θ\) satisfies this new equation, it may not satisfy the original equation because, to satisfy the original equation, we would need to be able to divide both sides of the equation by \(\cos θ\). However, if \(\cos θ=0\), we cannot divide both sides of the equation by \(\cos θ\). Therefore, it is possible that we may arrive at extraneous solutions. So, at the end, it is important to check for extraneous solutions. Returning to the equation, it is important that we factor \(\sin θ\) out of both terms on the left-hand side instead of dividing both sides of the equation by \(\sin θ\). Factoring the left-hand side of the equation, we can rewrite this equation as
\[\sin θ(2\cos^2θ−1)=0. \nonumber \]
Therefore, the solutions are given by the angles \(θ\) such that \(\sin θ=0\) or \(\cos^2θ=1/2\). The solutions of the first equation are \(θ=0,±π,±2π,….\) The solutions of the second equation are \(θ=π/4,(π/4)±(π/2),(π/4)±π,….\) After checking for extraneous solutions, the set of solutions to the equation is
\[θ=nπ \nonumber \]
and
\[θ=\dfrac{π}{4}+\dfrac{nπ}{2} \nonumber \]
with \(n=0,±1,±2,….\)
Find all solutions to the equation \(\cos(2θ)=\sin θ.\)
- Hint
-
Use the double-angle formula for cosine (Equation \ref{double1}).
- Answer
-
\(θ=\dfrac{3π}{2}+2nπ,\dfrac{π}{6}+2nπ,\dfrac{5π}{6}+2nπ\)
for \(n=0,±1,±2,…\).
Prove the trigonometric identity \(1+\tan^2θ=\sec^2θ.\)
Solution:
We start with the Pythagorean identity (Equation \ref{py1})
\[\sin^2θ+\cos^2θ=1. \nonumber \]
Dividing both sides of this equation by \(\cos^2θ,\) we obtain
\[\dfrac{\sin^2θ}{\cos^2θ}+1=\dfrac{1}{\cos^2θ}. \nonumber \]
Since \(\sin θ/\cos θ=\tan θ\) and \(1/\cos θ=\sec θ\), we conclude that
\[\tan^2θ+1=\sec^2θ. \nonumber \]
Prove the trigonometric identity \(1+\cot^2θ=\csc^2θ.\)
- Answer
-
Divide both sides of the identity \(\sin^2θ+\cos^2θ=1\) by \(\sin^2θ\).
Graphs and Periods of the Trigonometric Functions
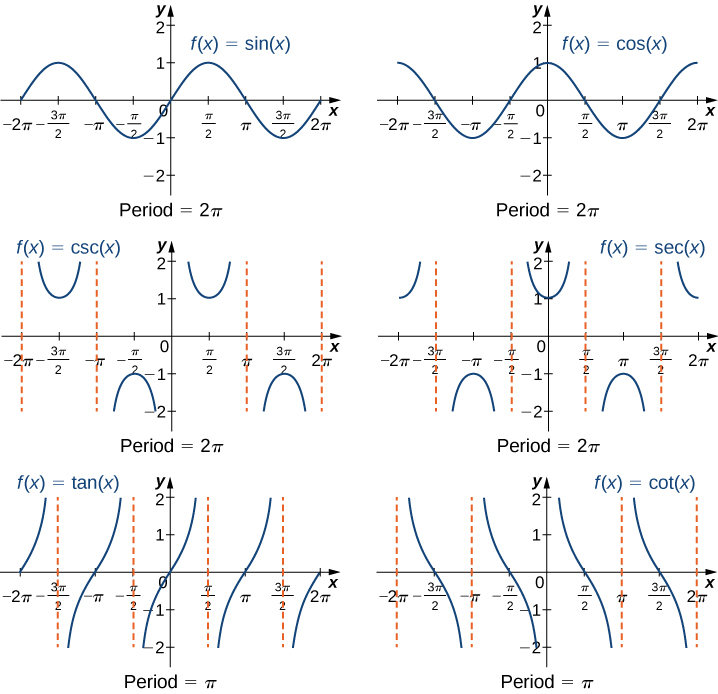
We have seen that as we travel around the unit circle, the values of the trigonometric functions repeat. We can see this pattern in the graphs of the functions. Let \(P=(x,y)\) be a point on the unit circle and let \(θ\) be the corresponding angle . Since the angle \(θ\) and \(θ+2π\) correspond to the same point \(P\), the values of the trigonometric functions at \(θ\) and at \(θ+2π\) are the same. Consequently, the trigonometric functions are periodic functions. The period of a function \(f\) is defined to be the smallest positive value \(p\) such that \(f(x+p)=f(x)\) for all values \(x\) in the domain of \(f\). The sine, cosine, secant, and cosecant functions have a period of \(2π\). Since the tangent and cotangent functions repeat on an interval of length \(π\), their period is \(π\) (Figure \(\PageIndex{5}\)).
Just as with algebraic functions, we can apply transformations to trigonometric functions. In particular, consider the following function:
\[f(x)=A\sin(B(x−α))+C. \nonumber \]
In Figure \(\PageIndex{6}\), the constant \(α\) causes a horizontal or phase shift. The factor \(B\) changes the period. This transformed sine function will have a period \(2π/|B|\). The factor \(A\) results in a vertical stretch by a factor of \(|A|\). We say \(|A|\) is the “amplitude of \(f\).” The constant \(C\) causes a vertical shift.

Notice in Figure \(\PageIndex{6}\) that the graph of \(y=\cos x\) is the graph of \(y=\sin x\) shifted to the left \(π/2\) units. Therefore, we can write
\[\cos x=\sin(x+π/2). \nonumber \]
Similarly, we can view the graph of \(y=\sin x\) as the graph of \(y=\cos x\) shifted right \(π/2\) units, and state that \(\sin x=\cos(x−π/2).\)
A shifted sine curve arises naturally when graphing the number of hours of daylight in a given location as a function of the day of the year. For example, suppose a city reports that June 21 is the longest day of the year with 15.7 hours and December 21 is the shortest day of the year with 8.3 hours. It can be shown that the function
\[h(t)=3.7\sin \left(\dfrac{2π}{365}(x−80.5)\right)+12 \nonumber \]
is a model for the number of hours of daylight \(h\) as a function of day of the year \(t\) (Figure \(\PageIndex{7}\)).
Sketch a graph of \(f(x)=3\sin(2(x−\frac{π}{4}))+1.\)
Solution
This graph is a phase shift of \(y=\sin (x)\) to the right by \(π/4\) units, followed by a horizontal compression by a factor of 2, a vertical stretch by a factor of 3, and then a vertical shift by 1 unit. The period of \(f\) is \(π\).
Describe the relationship between the graph of \(f(x)=3\sin(4x)−5\) and the graph of \(y=\sin(x)\).
- Hint
-
The graph of \(f\) can be sketched using the graph of \(y=\sin(x)\) and a sequence of three transformations.
- Answer
-
To graph \(f(x)=3\sin(4x)−5\), the graph of \(y=\sin(x)\) needs to be compressed horizontally by a factor of 4, then stretched vertically by a factor of 3, then shifted down 5 units. The function \(f\) will have a period of \(π/2\) and an amplitude of 3.
Key Concepts
- Radian measure is defined such that the angle associated with the arc of length 1 on the unit circle has radian measure 1. An angle with a degree measure of \(180\)° has a radian measure of \(\pi\) rad.
- For acute angles \(θ\),the values of the trigonometric functions are defined as ratios of two sides of a right triangle in which one of the acute angles is \(θ\).
- For a general angle \(θ\), let \((x,y)\) be a point on a circle of radius \(r\) corresponding to this angle \(θ\). The trigonometric functions can be written as ratios involving \(x\), \(y\), and \(r\).
- The trigonometric functions are periodic. The sine, cosine, secant, and cosecant functions have period \(2π\). The tangent and cotangent functions have period \(π\).
Key Equations
- Generalized sine function
\(f(x)=A \sin(B(x−α))+C\)
Glossary
- periodic function
- a function is periodic if it has a repeating pattern as the values of \(x\) move from left to right
- radians
- for a circular arc of length \(s\) on a circle of radius 1, the radian measure of the associated angle \(θ\) is \(s\)
- trigonometric functions
- functions of an angle defined as ratios of the lengths of the sides of a right triangle
- trigonometric identity
- an equation involving trigonometric functions that is true for all angles \(θ\) for which the functions in the equation are defined


