1.2E : Exercices pour la section 1.2

Last updated
Save as PDF

Page ID: 197958

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Dans les exercices 1 à 8, pour chaque paire de points,

a. trouvez la pente de la ligne passant par les points et

b. indique si la ligne est croissante, décroissante, horizontale ou verticale.

1)$(-2,4)$ et$(1,1)$

Réponse: a.$m = −1$
b. Décroissant

2)$(-1,4)$ et$(3,-1)$

3)$(3,5)$ et$(-1,2)$

Réponse: a.$m = 3/4$
b. Augmenter

4)$(6,4)$ et$(4,-3)$

5)$(2,3)$ et$(5,7)$

Réponse: a.$m = 4/3$
b. Augmenter

6)$(1,9)$ et$(-8,5)$

7)$(2,4)$ et$(1,4)$

Réponse: a.$m = 0$
b. Horizontal

8)$(1,4)$ et$(1,0)$

Dans les exercices 9 à 16, écrivez l'équation de la droite satisfaisant aux conditions données sous forme d'intersection de pente.

9) Pente =$−6$, traverse$(1,3)$

Réponse: $y=−6x+9$

10) Pente =$3$, traverse$(-3,2)$

11) Pente =$\frac{1}{3}$, traverse$(0,4)$

Réponse: $y=\frac{1}{3}x+4$

12) Pente =$\frac{2}{5}$,$x$ -intersection =$8$

13) En passant par$(2,1)$ et$(−2,−1)$

Réponse: $y=\frac{1}{2}x$

14) En passant par$(−3,7)$ et$(1,2)$

15)$x$ -intercept =$5$ et$y$ -intercept =$−3$

Réponse: $y=\frac{3}{5}x−3$

16)$x$ -Intercept =−$6$ et$y$ -intercept =$9$

Dans les exercices 17 à 24, pour chaque équation linéaire,

a. donner la pente$m$ et$y$ -intercepter, le$b,$ cas échéant, et

b. tracez la ligne.

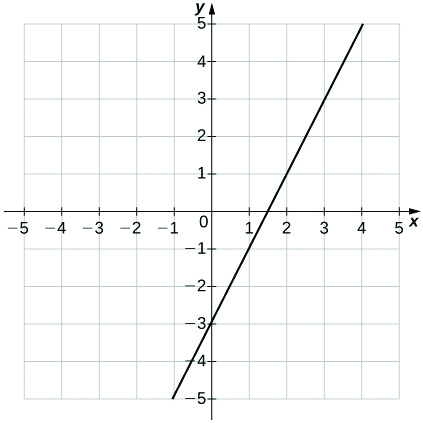
17)$y=2x−3$

Réponse

un.$m=2,\;b=−3$

$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique montre une fonction droite croissante avec une intersection y à (0, -3) et une intersection x à (1,5, 0).$

18)$y=−\frac{1}{7}x+1$

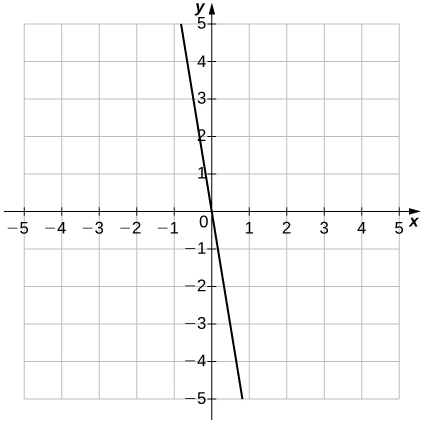
19)$f(x)=-6x$

Réponse

un.$m=−6,\; b=0$

$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique montre une fonction linéaire décroissante avec une intersection y et une intersection x à l'origine. Il existe un point non étiqueté sur la fonction à (0,5, -3).$

20)$f(x)=−5x+4$

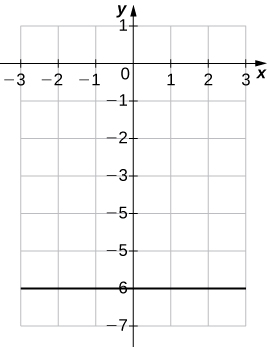
(21)$4y+24=0$

Réponse

un.$ m=0,\;b=−6$

$Image d'un graphique. L'axe x va de -3 à 3 et l'axe y va de -7 à 1. Le graphique montre une fonction de ligne droite horizontale avec une intersection y à (0, -6) et aucune intersection x.$

22)$8x-4=0$

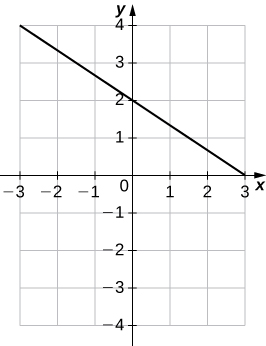
23)$2x+3y=6$

Réponse

un.$m=−\frac{2}{3},\; b=2$

$Image d'un graphique. L'axe x va de -3 à 3 et l'axe y va de -4 à 4. Le graphique montre une fonction linéaire décroissante avec une intersection y à (0, 2) et une intersection x à (3, 0).$

(24)$6x−5y+15=0$

Dans les exercices 25 à 29, pour chaque polynôme,

a. trouver le diplôme ;

b. trouvez les zéros, le cas échéant ;

c. trouvez le ou les$y$ -intercept (s), le cas échéant ;

d. utiliser le coefficient principal pour déterminer le comportement final du graphique ; et

e. déterminer algébriquement si le polynôme est pair, impair ou aucun des deux.

25)$f(x)=2x^2−3x−5$

Réponse: a.$2$
b.$\frac{5}{2},\;−1$ ;
c.$−5$
d. Les deux extrémités s'élèvent
e. Ni l'un ni l'autre

26)$f(x)=−3x^2+6x$

(27)$f(x)=\frac{1}{2}x^2−1$

Réponse: a.$2$
b. ±$\sqrt{2}$
c.$−1$
d. Les deux extrémités s'élèvent
e. Même

28)$f(x)=x^3+3x^2−x−3$

(29)$f(x)=3x−x^3$

Réponse: a.$3$
b.$0,$ ±$\sqrt{3}$
c.$0$
d. L'extrémité gauche s'élève, l'extrémité droite baisse
e. Odd

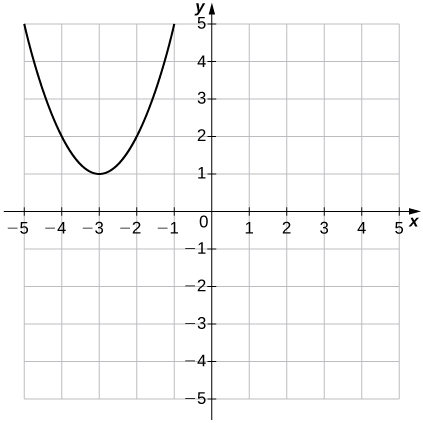
Pour les exercices 30 à 31, utilisez le graphique de$f(x)=x^2$ pour représenter graphiquement chaque fonction transformée$g$.

(30)$g(x)=x^2−1$

31)$g(x)=(x+3)^2+1$

Réponse: $Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique montre une fonction parabolique qui diminue jusqu'au point (-3, 1), puis commence à augmenter. L'intersection y n'est pas affichée et il n'y a pas d'interception x. Il y a deux points non tracés à (-4, 2) et (-2, 2).$

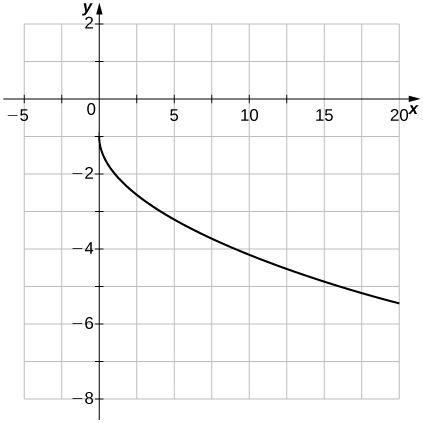
Pour les exercices 32 à 33, utilisez le graphique de$f(x)=\sqrt{x}$ pour représenter graphiquement chaque fonction transformée$g$.

32)$g(x)=\sqrt{x+2}$

33)$g(x)=−\sqrt{x}−1$

Réponse: $Image d'un graphique. L'axe x va de -5 à 20 et l'axe y va de -8 à 2. Le graphique montre une fonction courbe qui commence au point (0, -1), puis commence à décroître. L'intersection y est à (0, -1) et il n'y a pas d'intersection X. Il y a un point non tracé à (9, -4).$

Pour les exercices 34 à 35, utilisez le graphique de$y=f(x)$ pour représenter graphiquement chaque fonction transformée$g$.

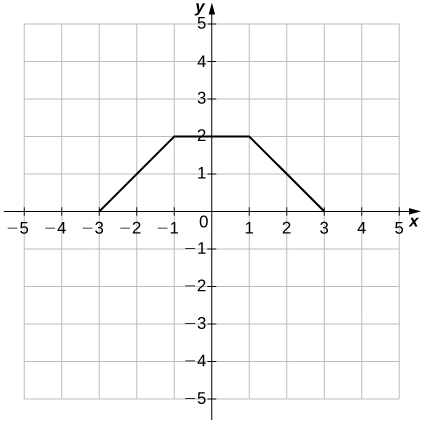
$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique montre une fonction qui commence au point (-3, 0), où elle commence à augmenter jusqu'au point (-1, 2). Après le point (-1, 2), la fonction devient une ligne horizontale et le reste jusqu'au point (1, 2). Après le point (1, 2), la fonction commence à diminuer jusqu'au point (3, 0), où la fonction se termine.$

34)$g(x)=f(x)+1$

35)$g(x)=f(x−1)+2$

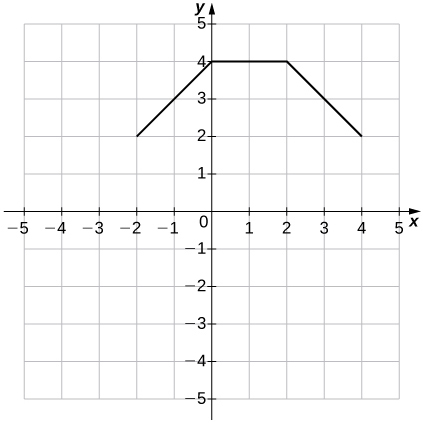
Réponse: $Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique montre une fonction qui commence au point (-2, 2), où elle commence à augmenter jusqu'au point (0, 4). Après le point (0, 4), la fonction devient une ligne horizontale et le reste jusqu'au point (2, 4). Après le point (2, 4), la fonction commence à diminuer jusqu'au point (4, 2), où la fonction se termine.$

Dans les exercices 36 à 39, pour chacune des fonctions définies au coup par coup,

a. évaluer aux valeurs données de la variable indépendante, et

b. esquissez le graphique.

36)$f(x)=\begin{cases}4x+3, & &\text{if } x≤0\\ -x+1, & &\text{if } x>0\end{cases} ;\quad f(−3);\; f(0);\; f(2)$

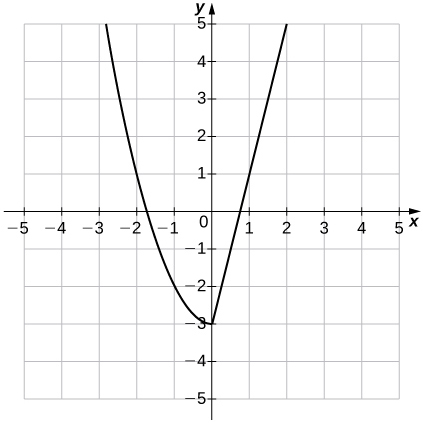
37)$f(x)=\begin{cases}x^2-3, & &\text{if } x≤0\\ 4x-3, & &\text{if } x>0\end{cases} ;\quad f(−4);\; f(0);\; f(2)$

Réponse

un.$f(−4) = 13,\quad f(0)=−3,\quad f(2)=5$

$Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphe représente une fonction composée de deux parties. La première pièce est une courbe décroissante qui se termine au point (0, -3). La deuxième pièce est une ligne croissante qui commence au point (0, -3). La fonction possède une intersection x au point approximatif (1,7, 0) et au point (0,75, 0) et une intersection y à (0, -3).$

38)$h(x)=\begin{cases}x+1, & &\text{if }x≤5\\4, & &\text{if } x>5\end{cases} ;\quad h(0);\; h(π);\; h(5)$

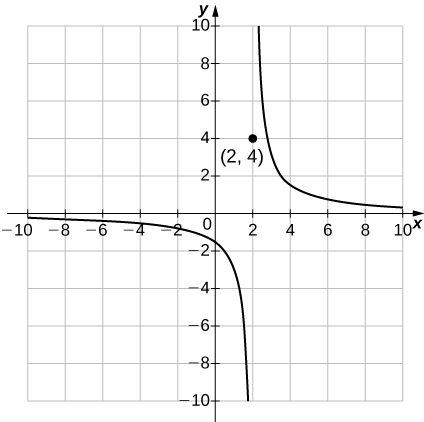
39)$g(x)=\begin{cases}\dfrac{3}{x−2}, & &\text{if }x≠2\\4, & &\text{if } x=2\end{cases} ;\quad g(0);\; g(−4);\; g(2)$

Réponse

un.$g(0) = -\frac{3}{2},\; g(-4)=-\frac{1}{2},\; g(2)=4$

$Image d'un graphique. L'axe x va de -10 à 10 et l'axe y va de -10 à 10. Le graphique représente une fonction qui commence légèrement en dessous de l'axe x et commence à diminuer. Lorsque la fonction s'approche de la ligne verticale non tracée de « x = 2 », elle diminue plus rapidement mais n'atteint jamais la droite « x = 2 ». Sur le côté droit de la ligne non tracée « x = 2 », la fonction commence en haut du graphique et commence à décroître pour se rapprocher de la ligne horizontale non tracée « y = 0 », mais n'atteint jamais « y = 0 ». Cette fonction inclut également un point tracé en (2, 4). Il y a une intersection y à (0, -1,5) et aucune intersection X.$

Dans les exercices 40 à 44, déterminez si l'énoncé est vrai ou faux. Expliquez pourquoi.

40)$f(x)=\dfrac{4x+1}{7x−2}$ est une fonction transcendantale.

41)$g(x)=\sqrt[3]{x}$ est une fonction racine étrange.

Réponse: C'est vrai ;$n=3$

42) Une fonction logarithmique est une fonction algébrique.

43) Une fonction de la forme$f(x)=x^b$, où$b$ est une constante à valeur réelle, est une fonction exponentielle.

Réponse: Faux ;$f(x)=x^b$, où$b$ est une constante à valeur réelle, est une fonction de puissance

44) Le domaine d'une fonction racine paire est constitué de nombres réels.

45) [L] Une entreprise achète du matériel informatique pour 20 500$. Au terme d'une période de 3 ans, la valeur de l'équipement a diminué de façon linéaire pour atteindre 12 301$.

a. Trouvez une fonction$y=V(t)$ qui détermine la valeur$V$ de l'équipement à la fin des$t$ années.

b. Trouvez et interprétez la signification des$x$$y$ - et des interceptions pour cette situation.

c. Quelle est la valeur de l'équipement au bout de 5 ans ?

d. Quand la valeur de l'équipement sera-t-elle de 3 000$ ?

Réponse: a.$V(t)=−2733t+20500$
b.$(0,20,500)$ signifie que le prix d'achat initial du matériel est de 20 500$ ;$(7.5,0)$ signifie que le matériel informatique n'a aucune valeur au$7.5$ fil des années.
c. 6 835 dollars
d. En quelques$6.4$ années

46) [T] Le nombre total d'achats en ligne pendant les vacances de Noël a augmenté de façon spectaculaire au cours des 5 dernières années. En 2012$(t=0)$, les ventes totales de vacances en ligne se sont élevées à 42,3 milliards de dollars, contre 48,1 milliards de dollars en 2013.

a. Trouvez une fonction linéaire$S$ qui estime le total des ventes en ligne pour les fêtes de fin d'année$t.$

b. Interpréter la pente du graphique de$S.$

c. Utilisez la partie a. pour prévoir l'année où les achats en ligne à Noël atteindront 60 milliards de dollars.

47) [T] Une boulangerie familiale fabrique des cupcakes et les vend lors de festivals locaux en plein air. Pour un festival de musique, il y a un coût fixe de 125$ pour installer un stand de cupcakes. Le propriétaire estime que la fabrication de chaque cupcake coûte 0,75$. Le propriétaire souhaite déterminer le coût total$C$ en fonction du nombre de cupcakes fabriqués.

a. Trouvez une fonction linéaire qui relie le coût$C$$x,$ au nombre de cupcakes fabriqués.

b. Déterminez le coût de la cuisson des$160$ cupcakes.

c. Si la propriétaire vend les cupcakes pour 1,50$ chacun, combien de cupcakes doit-elle vendre pour commencer à faire des bénéfices ? (Conseil : utilisez la fonction INTERSECTION d'une calculatrice pour trouver ce nombre.)

Réponse: a.$C=0.75x+125$
b. 245$
c.$167$ cupcakes

48) [L] Une maison achetée pour 250 000$ devrait valoir le double de son prix d'achat en 18 ans.

a. Trouvez une fonction linéaire qui modélise le prix$P$ de la maison par rapport au nombre d'années$t$ écoulées depuis l'achat initial.

b. Interpréter la pente du graphique de$P.$

c. Trouvez le prix de la maison des$15$ années à compter de son achat initial.

49) [L] Une voiture a été achetée pour 26 000$. La valeur de la voiture se déprécie de 1500$ par an.

a. Trouvez une fonction linéaire qui modélise la valeur$V$ de la voiture après des$t$ années.

b. Trouvez et interprétez$V(4)$.

Réponse: a.$V(t)=−1500t+26,000$
b. En$4$ années, la valeur de la voiture est de 20 000$.

50) [T] Un condominium situé dans un quartier chic de la ville a été acheté pour 432 000$. Au$35$ fil des années, il vaut 60 500$. Déterminez le taux d'amortissement.

51) [T] Le coût total$C$ (en milliers de dollars) de production d'un article donné est modélisé par la fonction$C(x)=10.50x+28,500$, où$x$ est le nombre d'articles produits. Déterminez le coût de production des$175$ articles.

Réponse: 30 337 500 dollars

52) [L] Une professeure demande à sa classe d'indiquer le temps$t$ qu'ils ont consacré à la rédaction de deux devoirs. La plupart des étudiants indiquent qu'il leur faut environ$45$ quelques minutes pour taper un devoir de quatre pages et environ des$1.5$ heures pour taper un devoir de neuf pages.

a. Trouvez la fonction linéaire$y=N(t)$ qui modélise cette situation, où$N$ est le nombre de pages saisies et$t$ le temps en minutes.

b. Utilisez la partie a. pour déterminer le nombre de pages que vous pouvez saisir en$2$ heures.

c. Utilisez la partie a. pour déterminer le temps nécessaire à la saisie d'un devoir de 20 pages.

53) [T] La production (en pourcentage de la capacité totale) des centrales nucléaires aux États-Unis peut être modélisée par la fonction$P(t)=1.8576t+68.052$, où$t$ est le temps en années et$t=0$ correspond au début de 2000. Utilisez le modèle pour prévoir le pourcentage de production en 2015.

Réponse: 96 % de la capacité totale

54) [T] Le bureau des admissions d'une université publique estime que 65 % des étudiants admis dans la promotion de 2019 s'inscriront réellement.

a. Trouvez la fonction linéaire$y=N(x)$, où$N$ est le nombre d'étudiants qui s'inscrivent réellement et$x$ le nombre de tous les étudiants admis à la promotion de 2019.

b. Si l'université souhaite que la taille des classes de première année en 2019 soit de 1 350 personnes, déterminez le nombre d'étudiants qui devraient être admis.

Contributeurs

Template:ContribOpenStaxCalc