1.2 : Classes de fonctions de base
- Page ID
- 197943
- Calculez la pente d'une fonction linéaire et interprétez sa signification.
- Reconnaissez le degré d'un polynôme.
- Trouvez les racines d'un polynôme quadratique.
- Décrivez les graphes des fonctions polynomiales paires et impaires de base.
- Identifiez une fonction rationnelle.
- Décrivez les graphes des fonctions de puissance et de racine.
- Expliquez la différence entre les fonctions algébriques et transcendantales.
- Tracez une fonction définie par morceaux.
- Esquissez le graphe d'une fonction qui a été décalée, étirée ou reflétée par rapport à sa position initiale sur le graphique.
Nous avons étudié les caractéristiques générales des fonctions. Examinons maintenant certaines classes de fonctions spécifiques. Nous commençons par passer en revue les propriétés de base des fonctions linéaires et quadratiques, puis nous généralisons pour inclure les polynômes de plus haut degré. En combinant des fonctions racines avec des polynômes, nous pouvons définir des fonctions algébriques générales et les distinguer des fonctions transcendantales que nous examinerons plus loin dans ce chapitre. Nous terminons la section avec des exemples de fonctions définies par morceaux et examinons comment esquisser le graphe d'une fonction qui a été décalée, étirée ou reflétée par rapport à sa forme initiale.
Fonctions linéaires et pente
Le type de fonction le plus simple à prendre en compte est une fonction linéaire. Les fonctions linéaires ont la forme\(f(x)=ax+b\), où\(a\) et\(b\) sont des constantes. Dans la figure\(\PageIndex{1}\), nous voyons des exemples de fonctions linéaires lorsque a est positif, négatif et zéro. Notez que si\(a>0\), le graphique de la droite augmente au fur et à mesure qu'il\(x\) augmente. En d'autres termes,\(f(x)=ax+b\) continue de croître\((−∞, ∞)\). Si\(a<0\), le graphique de la droite diminue à mesure qu'il\(x\) augmente. Dans ce cas,\(f(x)=ax+b\) est décroissant\((−∞, ∞)\). Si\(a=0\), la ligne est horizontale.
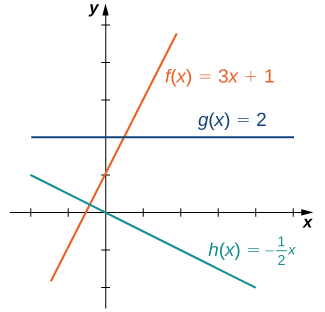
Comme le suggère la figure\(\PageIndex{1}\), le graphique de toute fonction linéaire est une ligne. L'une des caractéristiques distinctives d'une ligne est sa pente. La pente est la variation\(y\) pour chaque changement d'unité\(x\). La pente mesure à la fois la pente et la direction d'une ligne. Si la pente est positive, la ligne pointe vers le haut lorsqu'on se déplace de gauche à droite. Si la pente est négative, la ligne pointe vers le bas lorsqu'elle se déplace de gauche à droite. Si la pente est nulle, la ligne est horizontale. Pour calculer la pente d'une droite, nous devons déterminer le rapport entre la variation\(y\) de et la variation de\(x\). Pour ce faire, nous choisissons deux points quelconques,\((x_1,y_1)\) puis nous calculons\((x_2,y_2)\) sur la ligne\(\dfrac{y_2−y_1}{x_2−x_1}\). Sur la figure\(\PageIndex{2}\), nous voyons que ce ratio est indépendant des points choisis.
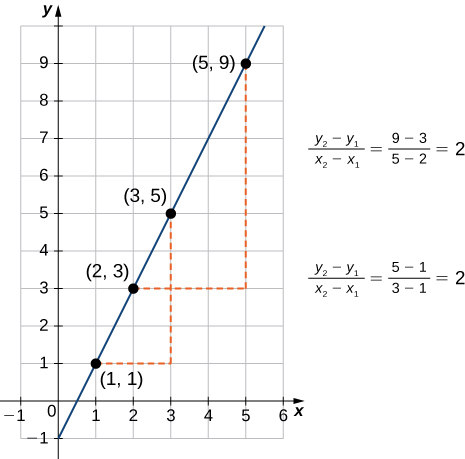
Considérez une ligne\(L\) passant par des points\((x_1,y_1)\) et\((x_2,y_2)\). Supposons\(Δy=y_2−y_1\)\(Δx=x_2−x_1\) et indiquez les changements dans\(y\) et\(x\), respectivement. La pente de la ligne est
\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{Δy}{Δx} \nonumber \]
Nous examinons maintenant la relation entre la pente et la formule d'une fonction linéaire. Considérez la fonction linéaire donnée par la formule\(f(x)=ax+b\). Comme indiqué précédemment, nous savons que le graphe d'une fonction linéaire est donné par une droite. Nous pouvons utiliser notre définition de pente pour calculer la pente de cette droite. Comme indiqué, nous pouvons déterminer la pente en calculant\((y_2−y_1)/(x_2−x_1)\) pour tous les points\((x_1,y_1)\) et\((x_2,y_2)\) sur la ligne. En évaluant la fonction\(f\) à\(x=0\), nous voyons qu'il\((0,b)\) s'agit d'un point sur cette ligne. En évaluant cette fonction à\(x=1\), nous voyons que\((1,a+b)\) c'est également un point sur cette ligne. Par conséquent, la pente de cette ligne est
\[\dfrac{(a+b)−b}{1−0}=a. \nonumber \]
Nous avons montré que le coefficient\(a\) est la pente de la droite. Nous pouvons en conclure que la formule\(f(x)=ax+b\) décrit une ligne avec pente\(a\). De plus, comme cette droite coupe l'\(y\)axe -au point\((0,b)\), nous voyons que l'\(y\)intersection -pour cette fonction linéaire est\((0,b)\). Nous concluons que la formule nous\(f(x)=ax+b\) indique\(a\) la pente et l'\(y\)intersection -pour cette droite.\((0,b)\) Comme nous utilisons souvent le symbole\(m\) pour indiquer la pente d'une ligne, nous pouvons écrire
\[\underbrace{f(x)=mx+b}_{\text{slope-intercept form}} \nonumber \]
pour indiquer la forme d'intersection de pente d'une fonction linéaire.
Parfois, il est pratique d'exprimer une fonction linéaire de différentes manières. Supposons, par exemple, que le graphe d'une fonction linéaire passe par le point\((x_1,y_1)\) et que la pente de la droite soit\(m\). Puisque tout autre point\((x,f(x))\) du graphe de\(f\) doit satisfaire à l'équation
\[m=\dfrac{f(x)−y_1}{x−x_1}, \nonumber \]
cette fonction linéaire peut être exprimée en écrivant
\[\underbrace{f(x)−y_1=m(x−x_1)}_{\text{point-slope equation}}. \nonumber \]
Nous appelons cette équation l'équation de pente ponctuelle pour cette fonction linéaire.
Comme chaque ligne non verticale est le graphe d'une fonction linéaire, les points d'une ligne non verticale peuvent être décrits à l'aide des équations de pente d'intersection ou de pente ponctuelle. Toutefois, une ligne verticale ne représente pas le graphe d'une fonction et ne peut être exprimée sous aucune de ces formes. Au lieu de cela, une ligne verticale est décrite par l'équation\(x=k\) d'une constante\(k\). Comme ni la forme pente-intersection ni la forme pente ponctuelle n'autorisent les lignes verticales, nous utilisons la notation
\[\underbrace{ax+by=c}_{\text{standard form}}, \nonumber \]
où\(a,b\) les deux sont différents de zéro, pour indiquer la forme standard d'une ligne.
Prenons l'exemple d'une ligne passant par le point\((x_1,y_1)\) incliné\(m\). L'équation
\[y−y_1=m(x−x_1) \nonumber \]
est l'équation de pente ponctuelle de cette droite.
Considérez une droite avec pente\(m\) et\(y\) -interceptez\((0,b).\) L'équation
\[y=mx+b \nonumber \]
est une équation de cette droite sous forme d'intersection de pente.
La forme standard d'une droite est donnée par l'équation
\[ax+by=c, \nonumber \]
où\(a\) et ne\(b\) sont pas tous les deux nuls. Ce formulaire est plus général car il permet de tracer une ligne verticale,\(x=k\).
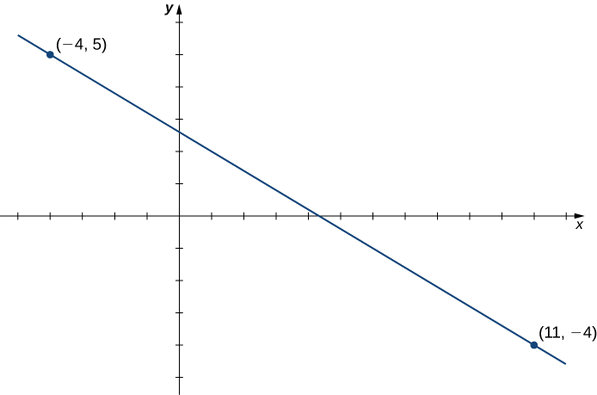
Considérez la ligne passant par les points\((11,−4)\) et\((−4,5)\), comme indiqué sur la figure\(\PageIndex{3}\).
- Détermine la pente de la ligne.
- Trouvez une équation pour cette fonction linéaire sous forme de pente ponctuelle.
- Trouvez une équation pour cette fonction linéaire sous forme d'intersection de pente.
Solution
1. La pente de la ligne est
\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{5−(−4)}{−4−11}=−\dfrac{9}{15}=−\dfrac{3}{5}. \nonumber \]
2. Pour trouver une équation pour la fonction linéaire sous forme de pente ponctuelle, utilisez la pente\(m=−3/5\) et choisissez n'importe quel point de la ligne. Si nous choisissons le point\((11,−4)\), nous obtenons l'équation
\[f(x)+4=−\dfrac{3}{5}(x−11). \nonumber \]
3. Pour trouver une équation pour la fonction linéaire sous forme d'intersection de pente, résolvez l'équation de la partie b. pour\(f(x)\). Lorsque nous faisons cela, nous obtenons l'équation
\[f(x)=−\dfrac{3}{5}x+\dfrac{13}{5}. \nonumber \]
Considérez la ligne passant par des points\((−3,2)\) et\((1,4)\).
- Détermine la pente de la ligne.
- Trouvez une équation de cette droite sous forme de pente ponctuelle.
- Trouvez une équation de cette droite sous forme d'intersection de pente.
- Allusion
-
La pente\(m=Δy/Δx\).
- Répondez à une
-
\(m=1/2\).
- Réponse b
-
La forme en pente ponctuelle est\(y−4=\dfrac{1}{2}(x−1)\).
- Réponse c
-
La forme d'interception de pente est\(y=\dfrac{1}{2}x+\dfrac{7}{2}\).
Jessica quitte sa maison à 5 h 50 et part courir 9 miles. Elle rentre chez elle à 7 h 08. Répondez aux questions suivantes, en supposant que Jessica court à un rythme constant.
- Décrivez la distance\(D\) (en miles) parcourue par Jessica comme une fonction linéaire de son temps de course\(t\) (en minutes).
- Esquissez un graphique de\(D\).
- Interprétez la signification de la pente.
Solution
a. Parfois\(t=0\), Jessica est chez elle, donc\(D(0)=0\). Au bout de\(t=78\) quelques minutes, Jessica a fini de courir\(9\) mi, donc\(D(78)=9\). La pente de la fonction linéaire est
\[m=\dfrac{9−0}{78−0}=\dfrac{3}{26}.\nonumber \]
Le\(y\) -intercept est\((0,0)\), donc l'équation de cette fonction linéaire est
\[D(t)=\dfrac{3}{26}t. \nonumber \]
b. Pour représenter un graphique\(D\), utilisez le fait que le graphe passe par l'origine et présente une pente\(m=3/26.\)
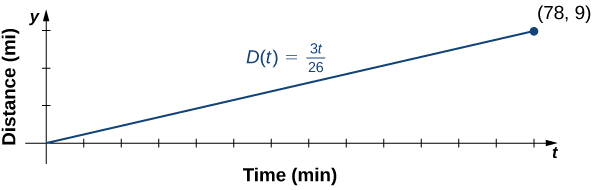
c. La pente\(m=3/26≈0.115\) décrit la distance (en miles) que Jessica parcourt par minute, ou sa vitesse moyenne.
Polynômes
Une fonction linéaire est un type spécial d'une classe plus générale de fonctions : les polynômes. Une fonction polynomiale est toute fonction qui peut être écrite sous la forme
\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0 \nonumber \]
pour certains entiers\(n≥0\) et constantes\(a_n,a_{n−1},…,a_0\), où\(a_n≠0\). Dans le cas où\(n=0\), nous autorisons\(a_0=0\) ; si\(a_0=0\), la fonction\(f(x)=0\) est appelée fonction zéro. La valeur\(n\) est appelée le degré du polynôme ; la constante\(a_n\) est appelée coefficient principal. Une fonction linéaire de la forme\(f(x)=mx+b\) est un polynôme de degré 1 si\(m≠0\) et de degré 0 si\(m=0\). Un polynôme de degré 0 est également appelé fonction constante. Une fonction polynomiale de degré 2 est appelée fonction quadratique. En particulier, une fonction quadratique a la forme
\[f(x)=ax^2+bx+c, \nonumber \]
où\(a≠0\). Une fonction polynomiale de degré\(3\) est appelée fonction cubique.
Fonctions d'alimentation
Certaines fonctions polynomiales sont des fonctions de puissance. Une fonction de puissance est n'importe quelle fonction de la forme\(f(x)=ax^b\), où\(a\) et\(b\) sont des nombres réels. L'exposant d'une fonction de puissance peut être n'importe quel nombre réel, mais nous considérons ici le cas où l'exposant est un entier positif. (Nous examinerons d'autres cas plus tard.) Si l'exposant est un entier positif, il\(f(x)=ax^n\) s'agit d'un polynôme. Si\(n\) est pair, alors\(f(x)=ax^n\) est une fonction paire parce que\(f(−x)=a(−x)^n=ax^n\)\(n\) c'est pair. Si\(n\) est impair, alors\(f(x)=ax^n\) est une fonction étrange car elle\(f(−x)=a(−x)^n=−ax^n\)\(n\) est étrange (Figure\(\PageIndex{4}\)).
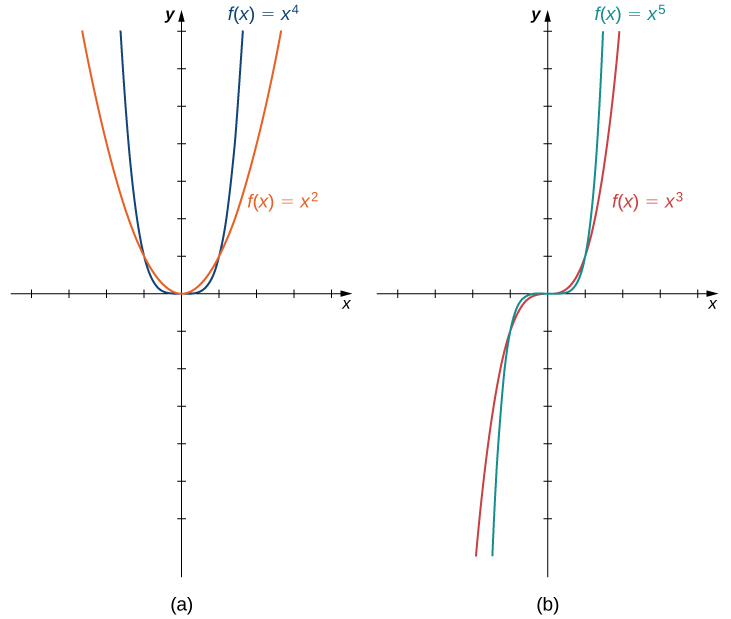
Un comportement à l'infini
Pour déterminer le comportement d'une fonction\(f\) lorsque les entrées approchent de l'infini, nous examinons les valeurs à\(f(x)\) mesure que les entrées augmentent.\(x\) Pour certaines fonctions, les valeurs de\(f(x)\) s'approchent d'un nombre fini. Par exemple, pour la fonction\(f(x)=2+1/x\), les valeurs\(1/x\) se rapprochent de plus en plus de zéro pour toutes les valeurs de à\(x\) mesure qu'elles augmentent. Pour cette fonction, nous disons «\(f(x)\) approche deux comme\(x\) ça va vers l'infini », et nous écrivons\(f(x)→2\) comme\(x→∞\). La droite\(y=2\) est une asymptote horizontale pour la fonction,\(f(x)=2+1/x\) car le graphe de la fonction se rapproche de la droite à mesure qu'il\(x\) s'agrandit.
Pour les autres fonctions, les valeurs\(f(x)\) peuvent ne pas s'approcher d'un nombre fini, mais peuvent augmenter pour toutes les valeurs à\(x\) mesure qu'elles augmentent. Dans ce cas, nous disons «\(f(x)\) s'approche de l'infini comme\(x\) s'approche de l'infini », et nous écrivons\(f(x)→∞\) comme\(x→∞\). Par exemple, pour la fonction\(f(x)=3x^2\), les sorties\(f(x)\) s'agrandissent à mesure que les entrées\(x\) s'agrandissent. Nous pouvons en conclure que la fonction s'\(f(x)=3x^2\)approche de l'infini comme elle\(x\) s'approche de l'infini, et nous écrivons\(3x^2→∞\) comme\(x→∞\). Le comportement en tant que\(x→∞\) ou\(x→−∞\) et la signification de «\(f(x)→−∞\) as »\(x→−∞\) peuvent être définis de la même manière. Nous pouvons décrire ce qu'il advient des valeurs de\(f(x)\) as\(x→∞\) et d'\(x→−∞\)as en tant que comportement final de la fonction.
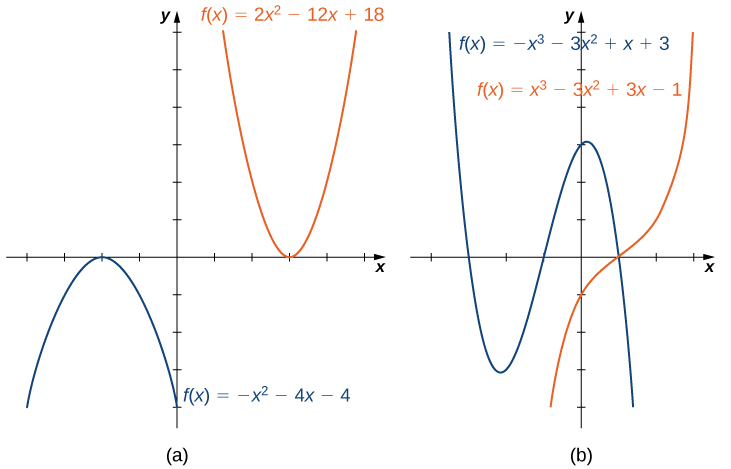
Pour comprendre le comportement final des fonctions polynomiales, nous pouvons nous concentrer sur les fonctions quadratiques et cubiques. Le comportement des polynômes de degré supérieur peut être analysé de la même manière. Prenons l'exemple d'une fonction quadratique\(f(x)=ax^2+bx+c\). Si\(a>0\), les valeurs sont\(f(x)→∞\) comme\(x→±∞\). Si\(a<0\), les valeurs sont\(f(x)→−∞\) comme\(x→±∞\). Puisque le graphe d'une fonction quadratique est une parabole, la parabole s'ouvre vers le haut si\(a>0\). ; la parabole s'ouvre vers le bas si\(a<0\) (Figure\(\PageIndex{5a}\)).
Considérons maintenant une fonction cubique\(f(x)=ax^3+bx^2+cx+d\). Si\(a>0\), alors au\(f(x)→∞\) fur\(x→∞\) et à\(f(x)→−∞\) mesure\(x→−∞\). Si\(a<0\), alors au\(f(x)→−∞\) fur\(x→∞\) et à\(f(x)→∞\) mesure\(x→−∞\). Comme nous pouvons le voir sur ces deux graphes, le terme principal du polynôme détermine le comportement final (Figure\(\PageIndex{5b}\)).
Zéros de fonctions polynomiales
Une autre caractéristique du graphe d'une fonction polynomiale est son intersection\(x\) avec l'axe. Pour déterminer où une fonction\(f\) croise l'\(x\)axe -, nous devons résoudre l'équation\(f(x)=0\) pour\(x\). Dans le cas de la fonction linéaire\(f(x)=mx+b\), le\(x\) -intercept est donné en résolvant l'équation\(mx+b=0\). Dans ce cas, nous voyons que le\(x\) -intercept est donné par\((−b/m,0)\). Dans le cas d'une fonction quadratique, pour trouver le ou les\(x\) -intercept (s), il faut trouver les zéros d'une équation quadratique :\(ax^2+bx+c=0\). Dans certains cas, il est facile de factoriser le polynôme\(ax^2+bx+c\) pour trouver les zéros. Dans le cas contraire, nous utilisons la formule quadratique.
Considérez l'équation quadratique
\[ax^2+bx+c=0, \nonumber \]
où\(a≠0\). Les solutions de cette équation sont données par la formule quadratique
\[x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}. \label{quad} \]
Si le discriminant\(b^2−4ac>0\), l'équation \ ref {quad} nous indique qu'il existe deux nombres réels qui satisfont l'équation quadratique. Si\(b^2−4ac=0\), cette formule nous indique qu'il n'y a qu'une seule solution, et c'est un nombre réel. Si\(b^2−4ac<0\), aucun nombre réel ne satisfait l'équation quadratique.
Dans le cas de polynômes de plus haut degré, il peut être plus compliqué de déterminer où le graphe croise l'\(x\)axe. Dans certains cas, il est possible de trouver les\(x\) -intercepts en factorisant le polynôme pour trouver ses zéros. Dans d'autres cas, il est impossible de calculer les valeurs exactes des\(x\) -intercepts. Cependant, comme nous le verrons plus loin dans le texte, dans de tels cas, nous pouvons utiliser des outils analytiques pour approximer (dans une très large mesure) l'emplacement des\(x\) -intercepts. Nous nous concentrons ici sur les graphes de polynômes pour lesquels nous pouvons calculer leurs zéros de manière explicite.
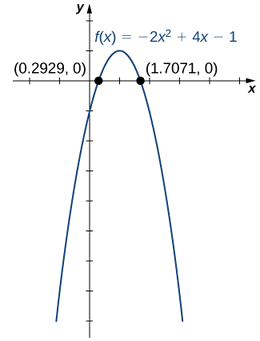
Pour les fonctions suivantes,
- \(f(x)=−2x^2+4x−1\)
- \(f(x)=x^3−3x^2−4x\)
- décrire le comportement d'un\(f(x)\) as\(x→±∞\),
- trouve tous les zéros de\(f\), et
- esquissez un graphique de\(f\).
Solution
1. La fonction\(f(x)=−2x^2+4x−1\) est une fonction quadratique.
1. Parce que\(a=−2<0\), comme\(x→±∞,f(x)→−∞.\)
2. Pour trouver les zéros de\(f\), utilisez la formule quadratique. Les zéros sont
\(x=\dfrac{−4±\sqrt{4^2−4(−2)(−1)}}{2(−2)}=\dfrac{−4±\sqrt{8}}{−4}=\dfrac{−4±2\sqrt{2}}{−4}=\dfrac{2±\sqrt{2}}{2}.\)
3. Pour esquisser le graphique de\(f\), utilisez les informations de vos réponses précédentes et combinez-les avec le fait que le graphique est une parabole s'ouvrant vers le bas.
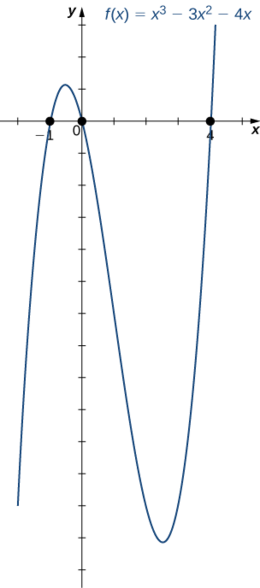
2. La fonction\(f(x)=x^3−3x^2−4x\) est une fonction cubique.
1. Parce que\(a=1>0\), comme\(x→∞\),\(f(x)→∞\). Comme\(x→−∞\),\(f(x)→−∞\).
2. Pour trouver les zéros de\(f\), nous devons factoriser le polynôme. Tout d'abord, lorsque nous\(x\) prenons en compte tous les termes, nous trouvons
\(f(x)=x(x^2−3x−4).\)
Ensuite, lorsque nous factorisons la fonction quadratique\(x^2−3x−4\), nous trouvons
\(f(x)=x(x−4)(x+1).\)
Par conséquent, les zéros de\(f\) sont\(x=0,4,−1\).
3. En combinant les résultats des parties i. et ii., dessinez une esquisse approximative de\(f\).
Considérez la fonction quadratique\(f(x)=3x^2−6x+2.\) Trouvez les zéros de\(f\). La parabole s'ouvre vers le haut ou vers le bas ?
- Allusion
-
Utilisez la formule quadratique.
- Réponse
-
Les zéros sont\(x=1±\sqrt{3}/3\). La parabole s'ouvre vers le haut.
Modèles mathématiques
Une grande variété de situations du monde réel peuvent être décrites à l'aide de modèles mathématiques. Un modèle mathématique est une méthode qui permet de simuler des situations réelles à l'aide d'équations mathématiques. Des physiciens, des ingénieurs, des économistes et d'autres chercheurs développent des modèles en combinant l'observation et des données quantitatives pour développer des équations, des fonctions, des graphes et d'autres outils mathématiques afin de décrire avec précision le comportement de divers systèmes. Les modèles sont utiles car ils permettent de prévoir les résultats futurs. Parmi les exemples de modèles mathématiques, citons l'étude de la dynamique des populations, les études des conditions météorologiques et les prévisions des ventes de produits.
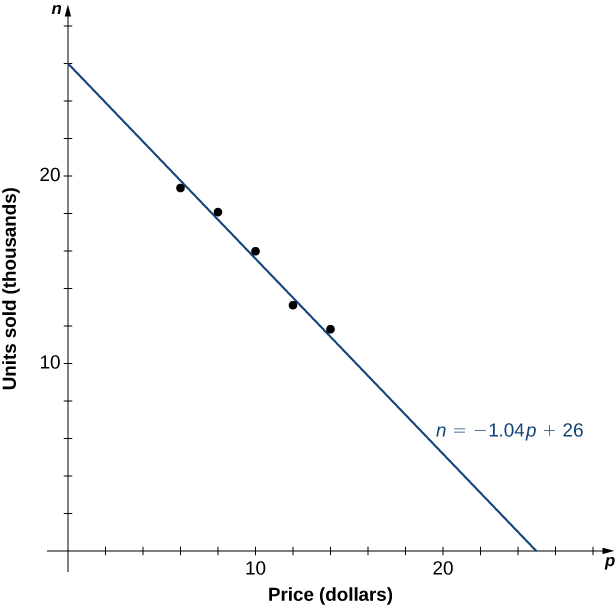
Prenons l'exemple d'un modèle mathématique qu'une entreprise pourrait utiliser pour décrire ses revenus liés à la vente d'un article en particulier. Le montant des revenus\(R\) qu'une entreprise perçoit pour la vente d'\(n\)articles vendus au prix de\(p\) dollars par article est décrit par l'équation\(R=p⋅n\). L'entreprise s'intéresse à l'évolution des ventes en fonction de l'évolution du prix de l'article. Supposons que les données du tableau\(\PageIndex{1}\) indiquent le nombre d'unités vendues par une entreprise en fonction du prix par article.
| \(p\) | 6 | 8 | 10 | 12 | 14 |
|---|---|---|---|---|---|
| \(n\) | 19,4 | 18,5 | 16,2 | 13,8 | 12,2 |
Dans la figure\(\PageIndex{6}\), nous voyons le graphique du nombre d'unités vendues (en milliers) en fonction du prix (en dollars). D'après la forme du graphique, nous remarquons que le nombre d'unités vendues est probablement une fonction linéaire du prix par article, et que les données peuvent être étroitement approximées à l'aide de la fonction linéaire\(n= −1.04p+26\) pour\(0≤p≤25\), où\(n\) prédit le nombre d'unités vendues en milliers. À l'aide de cette fonction linéaire, les recettes (en milliers de dollars) peuvent être estimées par la fonction quadratique
\[R(p)=p⋅ (−1.04p+26)=−1.04p^2+26p \text{ for }0≤p≤25. \nonumber \]
Dans l'exemple\(\PageIndex{4}\), nous utilisons cette fonction quadratique pour prédire le montant des revenus que l'entreprise perçoit en fonction du prix facturé par article. Notez que nous ne pouvons pas conclure de manière définitive le nombre réel d'unités vendues pour des valeurs de\(p\), pour lesquelles aucune donnée n'est collectée. Toutefois, compte tenu des autres valeurs de données et du graphique présenté, il semble raisonnable que le nombre d'unités vendues (en milliers) si le prix facturé est en\(p\) dollars soit proche des valeurs prédites par la fonction linéaire\(n=−1.04p+26.\)
Une entreprise souhaite prévoir le montant des revenus qu'elle percevra en fonction du prix qu'elle facture pour un article en particulier. À l'aide des données du tableau\(\PageIndex{1}\), l'entreprise arrive à la fonction quadratique suivante pour modéliser le chiffre\(R\) d'affaires en fonction du prix par article\(p:\)
\[R(p)=p⋅(−1.04p+26)=−1.04p^2+26p \nonumber \]
pour\(0≤p≤25\).
- Prédisez les revenus si l'entreprise vend l'article à un prix de\(p=$5\) et\(p=$17\).
- Trouvez les zéros de cette fonction et interprétez leur signification.
- Esquissez un graphique de\(R\).
- Utilisez le graphique pour déterminer la valeur de\(p\) ce qui maximise les revenus. Trouvez le maximum de revenus.
Solution
a. En évaluant la fonction des recettes à\(p=5\) et\(p=17\), nous pouvons conclure que
\(R(5)=−1.04(5)^2+26(5)=104,\text{ so revenue}=$104,000;\)
\(R(17)=−1.04(17)^2+26(17)=141.44,\text{ so revenue}=$141,440.\)
b. Les zéros de cette fonction peuvent être trouvés en résolvant l'équation\(−1.04p^2+26p=0\). Lorsque nous factorisons l'expression quadratique, nous obtenons\(p(−1.04p+26)=0\). Les solutions à cette équation sont données par\(p=0,25\). Pour ces valeurs de\(p\), le chiffre d'affaires est nul. Quand\(p=$0\), le chiffre d'affaires est nul parce que l'entreprise offre ses marchandises gratuitement. Quand\(p=$25\), le chiffre d'affaires est nul parce que le prix est trop élevé et que personne n'achètera d'articles.
c. Sachant que la fonction est quadratique, nous savons également que le graphe est une parabole. Le coefficient principal étant négatif, la parabole s'ouvre vers le bas. L'une des propriétés des paraboles est qu'elles sont symétriques par rapport à l'axe de symétrie, donc puisque les zéros se situent à\(p=0\) et\(p=25\), la parabole doit être symétrique par rapport à la ligne à mi-chemin entre eux, ou\(p=12.5\).
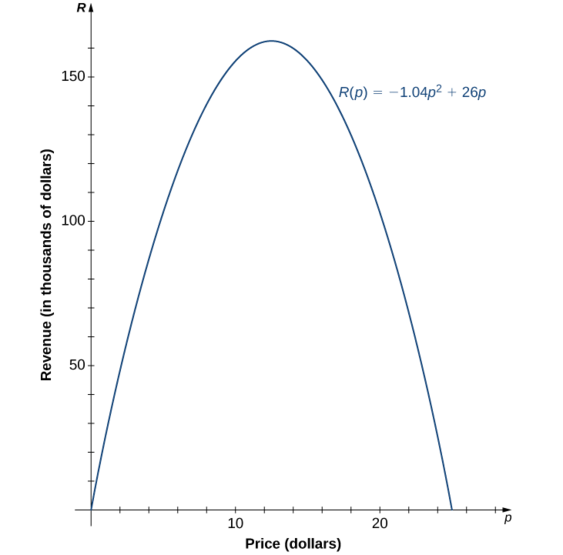
d. La fonction est une parabole avec des zéros à\(p=0\) et\(p=25\), et elle est symétrique par rapport à la ligne\(p=12.5\), de sorte que le revenu maximum est obtenu au prix\(p=$12.50\) par article. À ce prix, les recettes sont\(R(p)=−1.04(12.5)^2+26(12.5)=$162,500.\)
Fonctions algébriques
En tenant compte des quotients et des puissances fractionnaires dans les fonctions polynomiales, nous créons une classe de fonctions plus large. Une fonction algébrique est une fonction qui implique l'addition, la soustraction, la multiplication, la division, les pouvoirs rationnels et les racines. Deux types de fonctions algébriques sont les fonctions rationnelles et les fonctions racines.
Tout comme les nombres rationnels sont des quotients d'entiers, les fonctions rationnelles sont des quotients de polynômes. En particulier, une fonction rationnelle est toute fonction de la forme\(f(x)=p(x)/q(x)\), où\(p(x)\) et\(q(x)\) sont des polynômes. Par exemple,
\(f(x)=\dfrac{3x−1}{5x+2}\)et\(g(x)=\dfrac{4}{x^2+1}\)
sont des fonctions rationnelles. Une fonction racine est une fonction de puissance de la forme\(f(x)=x^{1/n}\), où\(n\) est un entier positif supérieur à un. Par exemple,\(f(x)=x^{1/2}=\sqrt{x}\) est la fonction racine carrée et\(g(x)=x^{1/3}=\sqrt[3]{x}\) la fonction racine cubique. En permettant des compositions de fonctions racines et de fonctions rationnelles, nous pouvons créer d'autres fonctions algébriques. Par exemple,\(f(x)=\sqrt{4−x^2}\) est une fonction algébrique.
Pour chacune des fonctions suivantes, recherchez le domaine et la plage.
- \(f(x)=\dfrac{3x−1}{5x+2}\)
- \(f(x)=\sqrt{4−x^2}\)
Solution
1. Il n'est pas possible de diviser par zéro, donc le domaine est l'ensemble des nombres réels\(x\) tels que\(x≠−2/5\). Pour trouver la plage, nous devons trouver les valeurs\(y\) pour lesquelles il existe un nombre réel\(x\) tel que
\(y=\dfrac{3x−1}{5x+2}\)
Lorsque nous multiplions les deux côtés de cette équation par\(5x+2\), nous voyons que cela\(x\) doit satisfaire à l'équation
\(5xy+2y=3x−1.\)
À partir de cette équation, nous pouvons voir que\(x\) doit satisfaire
\(2y+1=x(3−5y).\)
Si y=\(3/5\), cette équation n'a pas de solution. D'un autre côté, tant que\(y≠3/5\),
\(x=\dfrac{2y+1}{3−5y}\)
satisfait cette équation. Nous pouvons en conclure que la gamme\(f\) est\(\{y\,|\,y≠3/5\}\).
2. Pour trouver le domaine de\(f\), nous avons besoin de\(4−x^2≥0\). Lorsque nous prenons en compte, nous écrivons\(4−x^2=(2−x)(2+x)≥0\). Cette inégalité est valable si et seulement si les deux termes sont positifs ou si les deux termes sont négatifs. Pour que les deux termes soient positifs, nous devons trouver\(x\) que
\(2−x≥0\)et\(2+x≥0.\)
Ces deux inégalités se réduisent à\(2≥x\) et\(x≥−2\). Par conséquent, l'ensemble\(\{x\,|\,−2≤x≤2\}\) doit faire partie du domaine. Pour que les deux termes soient négatifs, il faut
\(2−x≤0\)et\(2+x\le 0.\)
Ces deux inégalités se réduisent également à\(2≤x\) et\(x\le −2\). Aucune valeur ne permet\(x\) de répondre à ces deux inégalités. Ainsi, nous pouvons conclure que le domaine de cette fonction est\(\{x\,|\,−2≤x≤2\}.\)
Si\(−2≤x≤2\), alors\(0≤4−x^2≤4\). Par conséquent\(0≤\sqrt{4−x2}≤2\), et la gamme de\(f\) est\(\{y\,|\,0≤y≤2\}.\)
Trouvez le domaine et la plage de la fonction\(f(x)=(5x+2)/(2x−1).\)
- Allusion
-
Le dénominateur ne peut pas être nul. Résolvez l'équation\(y=(5x+2)/(2x−1)\)\(x\) pour trouver la plage.
- Réponse
-
Le domaine est l'ensemble des nombres réels\(x\) tels que\(x≠1/2\). La gamme est l'ensemble\(\{y\,|\,y≠5/2\}\).
Les fonctions racines\(f(x)=x^{1/n}\) ont des caractéristiques qui les définissent selon qu'elles\(n\) sont paires ou impaires. Pour tous les entiers pairs\(n≥2\), le domaine de\(f(x)=x^{1/n}\) est l'intervalle\([0,∞)\). Pour tous les entiers impairs\(n≥1\), le domaine de\(f(x)=x^{1/n}\) est l'ensemble de tous les nombres réels. Puisque\(x^{1/n}=(−x)^{1/n}\) pour les entiers impairs\(n\),\(f(x)=x^{1/n}\) est une fonction étrange si elle\(n\) est impaire. Consultez les graphes des fonctions racines pour les différentes valeurs de\(n\) la figure\(\PageIndex{7}\).
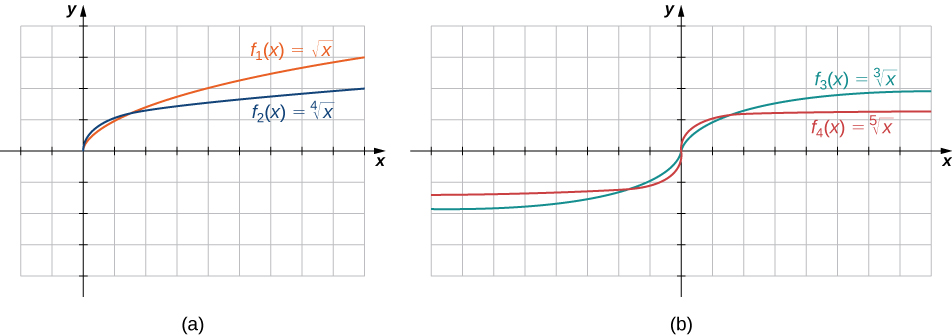
Pour chacune des fonctions suivantes, déterminez le domaine de la fonction.
- \(f(x)=\dfrac{3}{x^2−1}\)
- \(f(x)=\dfrac{2x+5}{3x^2+4}\)
- \(f(x)=\sqrt{4−3x}\)
- \(f(x)=\sqrt[3]{2x−1}\)
Solution
- Vous ne pouvez pas diviser par zéro, le domaine est donc l'ensemble de valeurs\(x\) tel que\(x^2−1≠0\). Par conséquent, le domaine est\(\{x\,|\,x≠±1\}\).
- Vous devez déterminer les valeurs\(x\) pour lesquelles le dénominateur est nul. Puisque\(3x^2+4≥4\) pour tous les nombres réels\(x\), le dénominateur n'est jamais zéro. Par conséquent, le domaine est\((−∞,∞).\)
- Puisque la racine carrée d'un nombre négatif n'est pas un nombre réel, le domaine est l'ensemble des valeurs\(x\) pour lesquelles\(4−3x≥0\). Par conséquent, le domaine est\(\{x\,|\,x≤4/3\}.\)
- La racine cubique est définie pour tous les nombres réels, de sorte que le domaine est l'intervalle\((−∞, ∞).\)
Trouvez le domaine pour chacune des fonctions suivantes :\(f(x)=(5−2x)/(x^2+2)\) et\(g(x)=\sqrt{5x−1}\).
- Allusion
-
Déterminez les valeurs\(x\) lorsque l'expression du dénominateur de\(f\) est différente de zéro et trouvez les valeurs\(x\) lorsque l'expression à l'intérieur du radical de\(g\) n'est pas négative.
- Réponse
-
Le domaine de\(f\) est\((−∞, ∞)\). Le domaine de\(g\) est\(\{x\,|\,x≥1/5\}.\)
Fonctions transcendantales
Jusqu'à présent, nous avons discuté des fonctions algébriques. Certaines fonctions ne peuvent toutefois pas être décrites par des opérations algébriques de base. Ces fonctions sont appelées fonctions transcendantales parce qu'on dit qu'elles « transcendent » ou vont au-delà de l'algèbre. Les fonctions transcendantales les plus courantes sont les fonctions trigonométriques, exponentielles et logarithmiques. Une fonction trigonométrique met en relation les rapports des deux côtés d'un triangle droit. Elles le sont\(\sin x, \cos x, \tan x, \cot x, \sec x,\text{ and }\csc x.\) (Nous aborderons les fonctions trigonométriques plus loin dans le chapitre.) Une fonction exponentielle est une fonction de la forme\(f(x)=b^x\), où se trouve la base\(b>0,\, b≠1\). Une fonction logarithmique est une fonction de la forme\(f(x)=\log_b(x)\) d'une constante\(b>0,\,b≠1,\) où\(\log_b(x)=y\) si et seulement si\(b^y=x\). (Nous aborderons également les fonctions exponentielles et logarithmiques plus loin dans le chapitre.)
Classez chacune des fonctions suivantes, a. à c., comme algébrique ou transcendantale.
- \(f(x)=\dfrac{\sqrt{x^3+1}}{4x+2}\)
- \(f(x)=2^{x^2}\)
- \( f(x)=\sin(2x)\)
Solution
- Comme cette fonction implique uniquement des opérations algébriques de base, il s'agit d'une fonction algébrique.
- Cette fonction ne peut pas être écrite comme une formule impliquant uniquement des opérations algébriques de base, elle est donc transcendantale. (Notez que les fonctions algébriques ne peuvent avoir que des puissances qui sont des nombres rationnels.)
- Comme dans la partie b, cette fonction ne peut pas être écrite à l'aide d'une formule impliquant uniquement des opérations algébriques de base ; par conséquent, cette fonction est transcendantale.
Est-ce\(f(x)=x/2\) une fonction algébrique ou transcendantale ?
- Réponse
-
Algébrique
Fonctions définies par morceaux
Parfois, une fonction est définie par différentes formules sur différentes parties de son domaine. Une fonction dotée de cette propriété est connue sous le nom de fonction définie par morceaux. La fonction de valeur absolue est un exemple de fonction définie par morceaux, car la formule change avec le signe suivant\(x\) :
\[f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}. \nonumber \]
D'autres fonctions définies par morceaux peuvent être représentées par des formules complètement différentes, selon la partie du domaine dans laquelle se situe un point. Pour représenter graphiquement une fonction définie par morceaux, nous tracons chaque partie de la fonction dans son domaine respectif, sur le même système de coordonnées. Si la formule d'une fonction est différente pour\(x<a\) et\(x>a\), nous devons porter une attention particulière à ce qui se passe\(x=a\) lorsque nous graphions la fonction. Parfois, le graphique doit inclure un cercle ouvert ou fermé pour indiquer la valeur de la fonction à\(x=a\). Nous examinerons cela dans l'exemple suivant.
Esquissez un graphique de la fonction suivante définie par pièces :
\[f(x)=\begin{cases}x+3, & \text{if } x<1\\(x−2)^2, & \text{if } x≥1\end{cases} \nonumber \]
Solution
Représentez graphiquement la fonction linéaire\(y=x+3\) sur l'intervalle\((−∞,1)\) et la fonction quadratique\(y=(x−2)^2\) sur l'intervalle\([1,∞)\). Puisque la valeur de la fonction at\(x=1\) est donnée par la formule\(f(x)=(x−2)^2\), nous voyons cela\(f(1)=1\). Pour l'indiquer sur le graphique, nous dessinons un cercle fermé au point\((1,1)\). La valeur de la fonction est donnée par\(f(x)=x+3\) for all\(x<1\), mais pas par at\(x=1\). Pour l'indiquer sur le graphique, nous dessinons un cercle ouvert à\((1,4)\).
2) Esquissez un graphique de la fonction
\(f(x)=\begin{cases}2−x, & \text{if } x≤2\\x+2, & \text{if } x>2\end{cases}.\)
Solution :
2. La fonction a une intersection x à (2, 0) et une intersection y à (0, 2)." src="https://math.libretexts.org/@api/dek...8509006001.png">
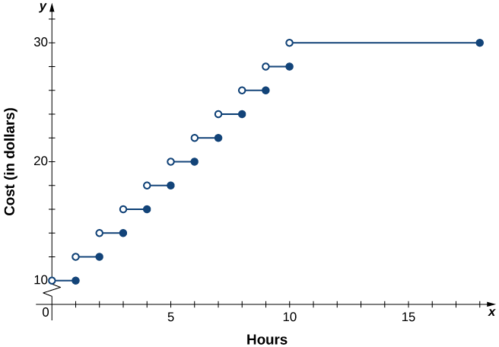
Dans une grande ville, les conducteurs doivent payer des tarifs variables pour se garer dans un garage. Ils sont facturés 10$ pour la première heure ou une partie de la première heure et 2$ supplémentaires pour chaque heure ou partie d'heure, jusqu'à un maximum de 30 dollars pour la journée. Le parking est ouvert de 6 h à minuit.
- Écrivez une fonction définie par morceaux qui décrit le coût\(C\) du stationnement dans le garage en fonction des heures de stationnement\(x\).
- Esquissez un graphique de cette fonction\(C(x).\)
Solution
1. Comme le parking est ouvert 18 heures par jour, le domaine de cette fonction est\(\{x\,|\,0<x≤18\}\). Le coût du stationnement d'une voiture dans ce garage peut être décrit par morceaux par la fonction
\[C(x)=\begin{cases}10, & \text{for } 0<x≤1\\12, & \text{for } 1<x≤2\\14, & \text{for } 2<x≤3\\16, & \text{for } 3<x≤4\\ ⋮\\30, & \text{for } 10<x≤18\end{cases}. \nonumber \]
2. Le graphique de la fonction se compose de plusieurs segments de ligne horizontaux.
Le coût de l'envoi d'une lettre est fonction du poids de la lettre. Supposons que le coût de l'envoi d'une lettre correspond\(49¢\) à la première once et\(21¢\) à chaque once supplémentaire. Écrivez une fonction définie par morceaux décrivant le coût\(C\) en fonction du poids\(x\) pour\(0<x≤3\), où\(C\) est mesuré en cents et\(x\) en onces.
- Allusion
-
La fonction définie par morceaux est constante sur les intervalles\((0,1],\,(1,2],\,….\)
- Réponse
-
\[C(x)=\begin{cases}49, 0<x≤1\\70, 1<x≤2\\91, 2<x≤3\end{cases} \nonumber \]
Transformations de fonctions
Nous avons vu plusieurs cas dans lesquels nous avons ajouté, soustrait ou multiplié des constantes pour former des variations de fonctions simples. Dans l'exemple précédent, par exemple, nous avons soustrait 2 de l'argument de la fonction\(y=x^2\) pour obtenir la fonction\(f(x)=(x−2)^2\). Cette soustraction représente un déplacement de la fonction de\(y=x^2\) deux unités vers la droite. Un décalage, horizontal ou vertical, est un type de transformation d'une fonction. Les autres transformations incluent les mises à l'échelle horizontale et verticale et les réflexions sur les axes.
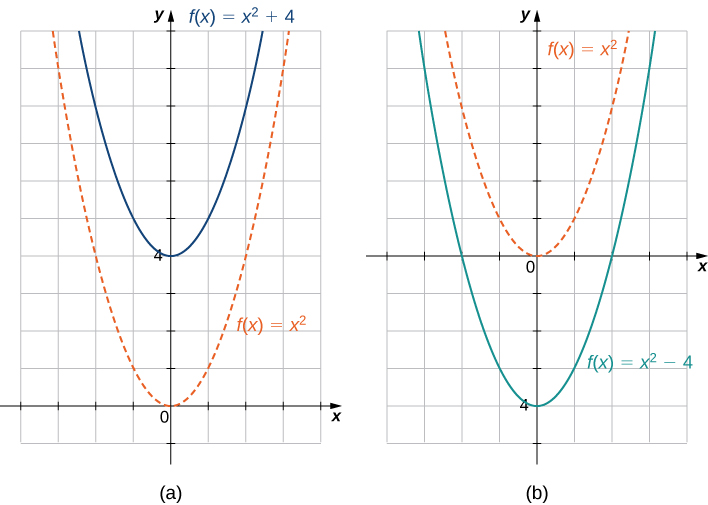
Un décalage vertical d'une fonction se produit si nous ajoutons ou soustrayons la même constante à chaque sortie\(y\). \(c>0\)En effet, le graphe de\(f(x)+c\) est un décalage du graphe des\(f(x)\)\(c\) unités supérieures, tandis que le graphe de\(f(x)−c\) est un décalage du graphe des\(c\) unités\(f(x)\) descendantes. Par exemple, le graphique de la fonction\(f(x)=x^3+4\) est le graphique des\(4\) unités\(y=x^3\) décalées vers le haut ; le graphique de la fonction\(f(x)=x^3−4\) est le graphique des\(4\) unités\(y=x^3\) décalées vers le bas (Figure\(\PageIndex{9}\)).
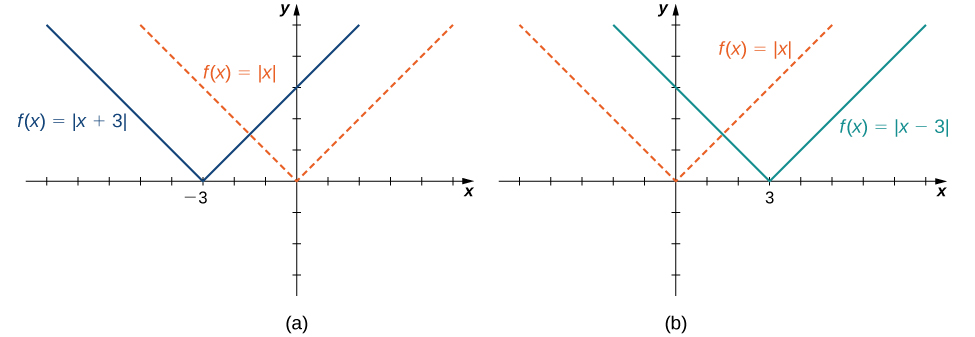
Un décalage horizontal d'une fonction se produit si nous ajoutons ou soustrayons la même constante à chaque entrée\(x\). \(c>0\)En effet, le graphe de\(f(x+c)\) est un décalage du graphe des\(c\) unités\(f(x)\) vers la gauche ; le graphique de\(f(x−c)\) est un décalage du graphe des\(c\) unités\(f(x)\) vers la droite. Pourquoi le graphique se déplace-t-il vers la gauche lors de l'ajout d'une constante et vers la droite lors de la soustraction d'une constante ? Pour répondre à cette question, prenons un exemple.
Examinez la fonction\(f(x)=|x+3|\) et évaluez-la à\(x−3\). Depuis\(f(x−3)=|x|\) et\(x−3<x\), le graphique de\(f(x)=|x+3|\) est le graphique des\(3\) unités\(y=|x|\) gauches décalées. De même, le graphique de\(f(x)=|x−3|\) est le graphique des\(3\) unités droites\(y=|x|\) décalées (Figure\(\PageIndex{10}\)).
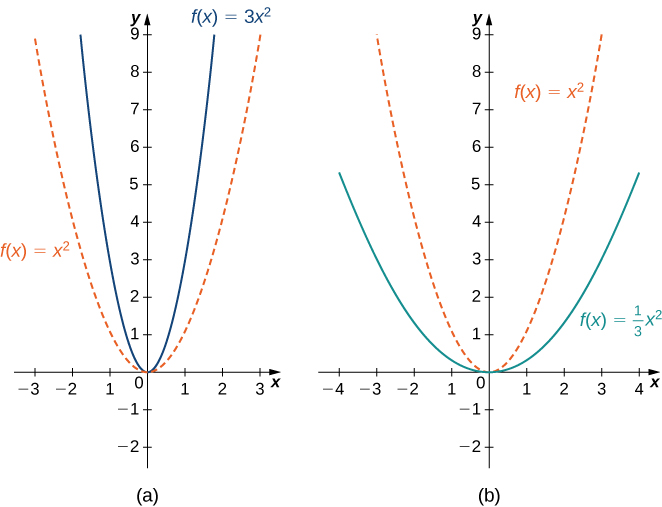
Une mise à l'échelle verticale d'un graphe se produit si nous multiplions toutes les sorties\(y\) d'une fonction par la même constante positive. \(c>0\)En effet, le graphe de la fonction\(cf(x)\) est le graphe de l'\(f(x)\)échelle verticale d'un facteur de\(c\). Si\(c>1\), les valeurs des sorties de la fonction\(cf(x)\) sont supérieures aux valeurs des sorties de la fonction\(f(x)\), le graphique a donc été étiré verticalement. Si\(0<c<1\), alors les sorties de la fonction\(cf(x)\) sont plus petites, le graphe a été compressé. Par exemple, le graphe de la fonction\(f(x)=3x^2\) est le graphique de l'\(y=x^2\)étirement vertical d'un facteur 3, tandis que le graphique de\(f(x)=x^2/3\) est le graphique de la\(y=x^2\) compression verticale d'un facteur de\(3\) (Figure\(\PageIndex{11b}\)).
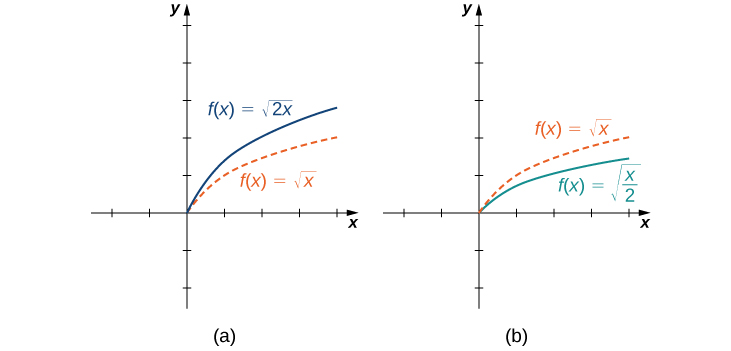
La mise à l'échelle horizontale d'une fonction se produit si nous multiplions les entrées\(x\) par la même constante positive. \(c>0\)En effet, le graphe de la fonction\(f(cx)\) est le graphique de l'\(f(x)\)échelle horizontale par un facteur de\(c\). Si\(c>1\), le graphe de\(f(cx)\) est le graphique de\(f(x)\) compressé horizontalement. Si\(0<c<1\), le graphique de\(f(cx)\) est le graphique de l'\(f(x)\)étirement horizontal. Par exemple, considérez la fonction\(f(x)=\sqrt{2x}\) et évaluez\(f\) à\(x/2\). Depuis\(f(x/2)=\sqrt{x}\), le graphe de\(f(x)=\sqrt{2x}\) est le graphe de\(y=\sqrt{x}\) compressé horizontalement. Le graphique de\(y=\sqrt{x/2}\) est un étirement horizontal du graphique de\(y=\sqrt{x}\) (Figure\(\PageIndex{12}\)).
Nous avons exploré ce qu'il advient du graphe d'une fonction\(f\) lorsque nous multiplions\(f\) par une constante\(c>0\) pour obtenir une nouvelle fonction\(cf(x)\). Nous avons également discuté de ce qu'il advient du graphe d'une fonction\(f\) lorsque nous multiplions la variable indépendante\(x\) par\(c>0\) pour obtenir une nouvelle fonction\(f(cx)\). Cependant, nous n'avons pas abordé ce qu'il advient du graphe de la fonction si la constante\(c\) est négative. Si nous avons une constante\(c<0\), nous pouvons écrire\(c\) comme un nombre positif multiplié par\(−1\) ; mais quel type de transformation obtenons-nous lorsque nous multiplions la fonction ou son argument par\(−1?\) Lorsque nous multiplions toutes les sorties par\(−1\), nous obtenons une réflexion sur l'\(x\)axe. Lorsque nous multiplions toutes les entrées par\(−1\), nous obtenons une réflexion sur l'\(y\)axe. Par exemple, le graphique de\(f(x)=−(x^3+1)\) est le graphique de la\(y=(x^3+1)\) réflexion autour de l'\(x\)axe. Le graphique de\(f(x)=(−x)^3+1\) est le graphique de la\(y=x^3+1\) réflexion autour de l'\(y\)axe (Figure\(\PageIndex{13}\)).
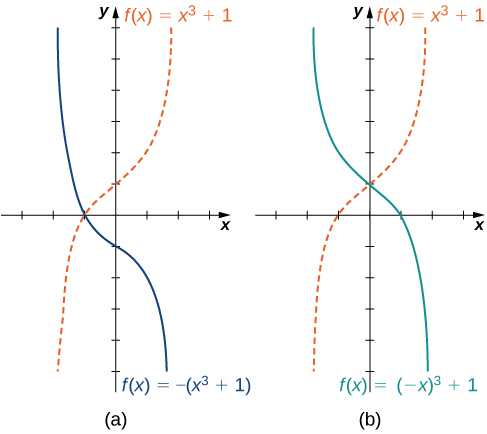
Si le graphe d'une fonction consiste en plusieurs transformations d'un autre graphe, il est important de transformer le graphe dans le bon ordre. Étant donné une fonction\(f(x)\), le graphe de la fonction associée\(y=cf(a(x+b))+d\) peut être obtenu à partir du graphe de en\(y=f(x)\) effectuant les transformations dans l'ordre suivant.
- Déplacement horizontal du graphique de\(y=f(x)\). Si\(b>0\), décalez vers la gauche. Si vous\(b<0\) changez à droite.
- Mise à l'échelle horizontale du graphique\(y=f(x+b)\) d'un facteur de\(|a|\). Si\(a<0\), reflétez le graphique autour de l'\(y\)axe.
- Mise à l'échelle verticale du graphique\(y=f(a(x+b))\) d'un facteur de\(|c|\). Si\(c<0\), reflétez le graphique autour de l'\(x\)axe.
- Déplacement vertical du graphique de\(y=cf(a(x+b))\). Si\(d>0\), passez à la vitesse supérieure. Si\(d<0\), déplacez-vous vers le bas.
Nous pouvons résumer les différentes transformations et leurs effets connexes sur le graphique d'une fonction dans le tableau suivant.
| Transformation de\(f (c>0)\) | Effet du graphe de\(f\) |
|---|---|
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(f(x)+c\) | \ (f \) » style="text-align:center ; vertical-align:middle ; "\(c\)>Unités de décalage vertical |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(f(x)-c\) | \ (f \) » style="text-align:center ; vertical-align:middle ; "\(c\)>Unités de décalage vertical |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(f(x+c)\) | \ (f \) » style="text-align:center ; vertical-align:middle ; ">Déplacer vers la gauche par\(c\) unités |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(f(x-c)\) | \ (f \) » style="text-align:center ; vertical-align:middle ; ">Déplacer vers la droite par\(c\) unités |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(cf(x)\) | \ (f \) » style="vertical-align:middle ; « >
Étirement vertical si\(c>1\) ; compression verticale si\(0<c<1\) |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(f(cx)\) | \ (f \) » style="vertical-align:middle ; « >
Étirement horizontal\(0<c<1\) ; compression horizontale si\(c>1\) |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(-f(x)\) | \ (f \) » style="text-align:center ; vertical-align:middle ; ">Réflexion sur l'\(x\)axe |
| \ (f (c>0) \) » style="text-align:center ; vertical-align:middle ; « >\(f(-x)\) | \ (f \) » style="text-align:center ; vertical-align:middle ; ">Réflexion sur l'\(y\)axe |
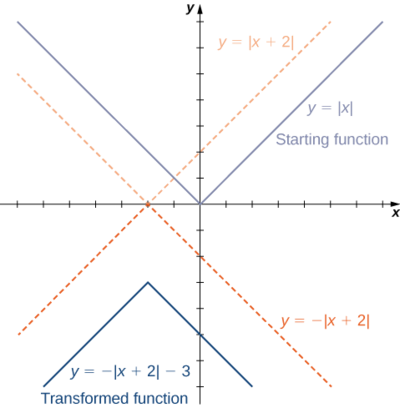
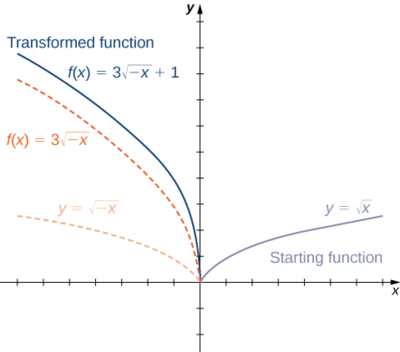
Pour chacune des fonctions suivantes, a. et b., esquissez un graphe à l'aide d'une séquence de transformations d'une fonction connue.
- \(f(x)=−|x+2|−3\)
- \(f(x)=\sqrt[3]{x}+1\)
Solution
1. En commençant par le graphique de\(y=|x|\), déplacez les\(2\) unités vers la gauche, réfléchissez autour de l'\(x\)axe Y, puis déplacez les\(3\) unités vers le bas.
2. En commençant par le graphique de\(y=sqrt{x},\) réflexion autour de\(y\) l'axe Y, étirez le graphique verticalement d'un facteur 3 et augmentez d'une unité.
Décrire comment la fonction\(f(x)=−(x+1)^2−4\) peut être représentée graphiquement à l'aide du graphe\(y=x^2\) et d'une séquence de transformations
- Réponse
-
Déplace le graphique\(y=x^2\) d'une unité vers la gauche, réfléchis autour de l'\(x\)axe des s, puis décale de 4 unités vers le bas.
Concepts clés
- La fonction de puissance\(f(x)=x^n\) est une fonction paire si n est pair et\(n≠0\), et c'est une fonction impaire si elle\(n\) est impair.
- La fonction root\(f(x)=x^{1/n}\) possède le domaine\([0,∞)\) si n est pair et le domaine\((−∞,∞)\) if\(n\) est impair. Si\(n\) est impair, alors\(f(x)=x^{1/n}\) est une fonction étrange.
- Le domaine de la fonction rationnelle\(f(x)=p(x)/q(x)\), où\(p(x)\) et\(q(x)\) sont des fonctions polynomiales, est l'ensemble de\(x\) ces fonctions\(q(x)≠0\).
- Les fonctions qui impliquent les opérations de base d'addition, de soustraction, de multiplication, de division et de puissances sont des fonctions algébriques. Toutes les autres fonctions sont transcendantales. Les fonctions trigonométriques, exponentielles et logarithmiques sont des exemples de fonctions transcendantales.
- Une fonction polynomiale\(f\) avec degré\(n≥1\) satisfait\(f(x)→±∞\) à\(x→±∞\). Le signe de la sortie\(x→∞\) dépend uniquement du signe du coefficient principal et du fait qu'il\(n\) soit pair ou impair.
- Les décalages verticaux et horizontaux, les mises à l'échelle verticale et horizontale et les réflexions sur les\(y\) axes\(x\) - et - sont des exemples de transformations de fonctions.
Équations clés
- Équation de pente ponctuelle d'une droite\[y−y_1=m(x−x_1)\nonumber \]
- Forme d'intersection en pente d'une ligne\[y=mx+b\nonumber \]
- Forme standard d'une ligne\[ax+by=c\nonumber \]
- Fonction polynomiale\[f(x)=a_n{x^n}+a_{n−1}x^{n−1}+⋯+a_1x+a_0\nonumber \]
Lexique
- fonction algébrique
- une fonction impliquant une combinaison des seules opérations de base d'addition, de soustraction, de multiplication, de division, de puissances et de racines appliquées à une variable d'entrée\(x\)
- fonction cubique
- un polynôme de degré 3, c'est-à-dire une fonction de la forme\(f(x)=ax^3+bx^2+cx+d\), où\(a≠0\)
- diplôme
- pour une fonction polynomiale, la valeur du plus grand exposant d'un terme
- fonction linéaire
- une fonction qui peut être écrite dans le formulaire\(f(x)=mx+b\)
- fonction logarithmique
- une fonction de la forme\(f(x)=\log_b(x)\) pour une base\(b>0,\,b≠1\) telle que\(y=\log_b(x)\) si et seulement si\(b^y=x\)
- modèle mathématique
- Une méthode de simulation de situations réelles à l'aide d'équations mathématiques
- fonction définie par morceaux
- une fonction définie différemment selon les différentes parties de son domaine
- équation de pente ponctuelle
- équation d'une fonction linéaire indiquant sa pente et un point sur le graphe de la fonction
- fonction polynomiale
- une fonction du formulaire\(f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0\)
- fonction d'alimentation
- une fonction de la forme\(f(x)=x^n\) pour tout entier positif\(n≥1\)
- fonction quadratique
- un polynôme de degré 2, c'est-à-dire une fonction de la forme\(f(x)=ax^2+bx+c\) où\(a≠0\)
- fonction rationnelle
- une fonction de la forme\(f(x)=p(x)/q(x)\), où\(p(x)\) et\(q(x)\) sont des polynômes
- fonction racine
- une fonction de la forme\(f(x)=x^{1/n}\) pour n'importe quel entier\(n≥2\)
- pente
- la variation\(y\) pour chaque changement d'unité\(x\)
- formulaire d'interception de pente
- équation d'une fonction linéaire indiquant sa pente et son\(y\) intersection
- fonction transcendantale
- une fonction qui ne peut pas être exprimée par une combinaison d'opérations arithmétiques de base
- transformation d'une fonction
- un décalage, une mise à l'échelle ou le reflet d'une fonction


