Skip to main content
Global

1.1E : Exercices pour la section 1.1

  1. Last updated
  2. Save as PDF
  • Page ID
    198003

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Pour les exercices 1 à 6, (a) déterminez le domaine et la plage de chaque relation, et (b) indiquez si la relation est une fonction.

    1)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >9 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >4 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >4
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >9
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >
    Réponse

    a. Domaine = {\(−3,−2,−1,0,1,2,3\)}, plage = {\(0,1,4,9\)}

    b. Oui, une fonction

    2)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >-2 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >-8 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >8
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >-1 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >-2
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >

    3)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >-3 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >-2 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >2
    \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >-1 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >3
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >
    Réponse

    a. Domaine = {\(0,1,2,3\)}, plage = {\(−3,−2,−1,0,1,2,3\)}

    b. Non, ce n'est pas une fonction

    4)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « >5 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « >6 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « >7 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >4 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >

    5)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >3 \ (x \) » style="text-align:center ; « >15 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >5 \ (y \) » style="text-align:center ; « >2 \ (x \) » style="text-align:center ; « >21 \ (y \) » style="text-align:center ; « >2
    \ (x \) » style="text-align:center ; « >8 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « >33 \ (y \) » style="text-align:center ; « >3
    \ (x \) » style="text-align:center ; « >10 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >
    Réponse

    a. Domaine = {\(3,5,8,10,15,21,33\)}, plage = {\(0,1,2,3\)}

    b. Oui, une fonction

    6)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-7 \ (y \) » style="text-align:center ; « >11 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >-2
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >5 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >4
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « >6 \ (y \) » style="text-align:center ; « >11
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >-1 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >

    Pour les exercices 7 à 13, trouvez les valeurs de chaque fonction, si elles existent, puis simplifiez.

    a.\(f(0)\) b.\(f(1)\) c.\(f(3)\) d.\(f(−x)\) e.\(f(a)\) f.\(f(a+h)\)

    7)\(f(x)=5x−2\)

    Réponse
    a.\(−2\) b.\(3\) c.\(13\) d.\(−5x−2\) e.\(5a−2\) f.\(5a+5h−2\)

    8)\(f(x)=4x^2−3x+1\)

    9)\(f(x)=\dfrac{2}{x}\)

    Réponse
    a. Non défini b.\(2\) c.\(\frac{2}{3}\) d.\(−\dfrac{2}{x}\) e.\(\dfrac{2}{a}\) f.\(\dfrac{2}{a+h}\)

    10)\(f(x)=|x−7|+8\)

    11)\(f(x)=\sqrt{6x+5}\)

    Réponse
    a.\(\sqrt{5}\) b.\(\sqrt{11}\) c.\(\sqrt{23}\) d.\(\sqrt{−6x+5}\) e.\(\sqrt{6a+5}\) f.\(\sqrt{6a+6h+5}\)

    (12)\(f(x)=\dfrac{x−2}{3x+7}\)

    13)\(f(x)=9\)

    Réponse
    a. 9 b. 9 c. 9 d. 9 e. 9 f. 9

    Pour les exercices 14 à 21, trouvez le domaine, la plage et tous les zéros/interceptions, le cas échéant, des fonctions.

    (14)\(f(x)=\dfrac{x}{x^2−16}\)

    15)\(g(x)=\sqrt{8x−1}\)

    Réponse
    \(x≥\frac{1}{8};\quad y≥0;\quad x=\frac{1}{8}\); pas d'interception en Y

    16)\(h(x)=\dfrac{3}{x^2+4}\)

    17)\(f(x)=−1+\sqrt{x+2}\)

    Réponse
    \(x≥−2;\quad y≥−1;\quad x=−1;\quad y=−1+\sqrt{2}\)

    18)\(f(x)=1x−\sqrt{9}\)

    19)\(g(x)=\dfrac{3}{x−4}\)

    Réponse
    \(x≠4;\quad y≠0\); aucune interception X ;\(y=−\frac{3}{4}\)

    (20)\(f(x)=4|x+5|\)

    (21)\(g(x)=\sqrt{\dfrac{7}{x−5}}\)

    Réponse
    \(x>5;\quad y>0\); aucune interception

    Pour les exercices 22 à 27, créez un tableau pour esquisser le graphique de chaque fonction à l'aide des valeurs suivantes :\(x=−3,−2,−1,0,1,2,3.\)

    22)\(f(x)=x^2+1\)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >10 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >2
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >5 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >5
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >2 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >10
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >

    23)\(f(x)=3x−6\)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >-15 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >-3
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >-12 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >0
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >-9 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >3
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >-6 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >
    Réponse
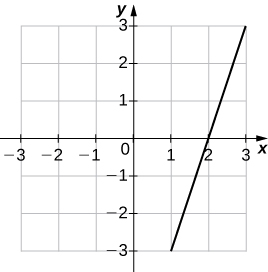
    Image d'un graphique. L'axe x va de -3 à 3 et l'axe y va de -3 à 3. Le graphique représente la fonction « f (x) = 3x - 6 », qui est une ligne droite croissante. La fonction possède une intersection x à (2, 0) et l'intersection y n'est pas affichée.

    (24)\(f(x)=\frac{1}{2}x+1\)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >\(-\frac{1}{2}\) \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >\(\frac{3}{2}\)
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >2
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >\(\frac{1}{2}\) \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >\(\frac{5}{2}\)
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >1 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >

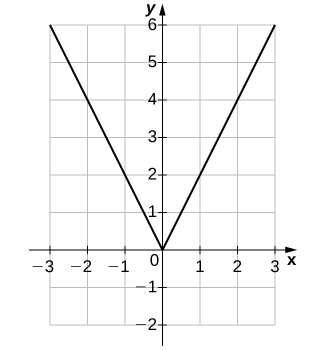
    25)\(f(x)=2|x|\)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >6 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >2
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >4 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >4
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >2 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >6
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >
    Réponse
    Image d'un graphique. L'axe x va de -3 à 3 et l'axe y va de -2 à 6. Le graphique représente la fonction « f (x) = 2 fois la valeur absolue de x ». La fonction diminue en ligne droite jusqu'à atteindre l'origine, puis commence à augmenter en ligne droite. Les fonctions x intercept et y intercept sont à l'origine.

    26)\(f(x)=-x^2\)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >-9 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >-1
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >-4 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >-4
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >-1 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >-9
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >

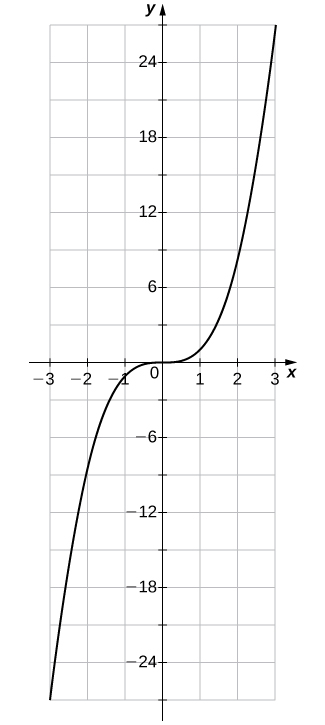
    (27)\(f(x)=x^3\)

    \(x\) \(y\) \(x\) \(y\)
    \ (x \) » style="text-align:center ; « >-3 \ (y \) » style="text-align:center ; « >-27 \ (x \) » style="text-align:center ; « >1 \ (y \) » style="text-align:center ; « >1
    \ (x \) » style="text-align:center ; « >-2 \ (y \) » style="text-align:center ; « >-8 \ (x \) » style="text-align:center ; « >2 \ (y \) » style="text-align:center ; « >8
    \ (x \) » style="text-align:center ; « >-1 \ (y \) » style="text-align:center ; « >-1 \ (x \) » style="text-align:center ; « >3 \ (y \) » style="text-align:center ; « >27
    \ (x \) » style="text-align:center ; « >0 \ (y \) » style="text-align:center ; « >0 \ (x \) » style="text-align:center ; « > \ (y \) » style="text-align:center ; « >
    Réponse
    Image d'un graphique. L'axe x va de -3 à 3 et l'axe y va de -27 à 27. Le graphique représente la fonction « f (x) = x cube ». La fonction incurvée augmente jusqu'à atteindre l'origine, où elle se stabilise puis devient uniforme. Après l'origine, le graphique recommence à augmenter. L'intersection x et l'intersection y sont toutes deux à l'origine.

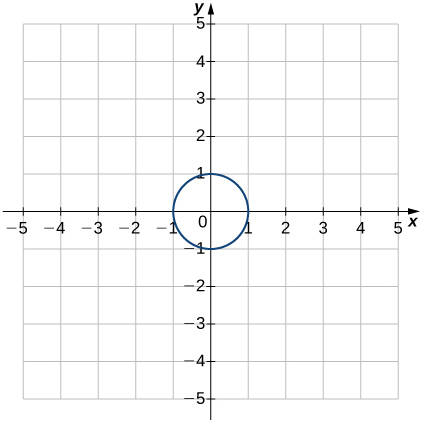
    Pour les exercices 28 à 35, utilisez le test de la ligne verticale pour déterminer si chacun des graphes donnés représente une fonction. Supposons qu'un graphe continue à ses deux extrémités s'il s'étend au-delà de la grille donnée. Si le graphique représente une fonction, déterminez ce qui suit pour chaque graphique :

    a. Domaine et gamme

    b.\(x\) -intercepter, le cas échéant (estimation si nécessaire)

    c.\(y\) -Interception, le cas échéant (estimation si nécessaire)

    d. Les intervalles pour lesquels la fonction augmente

    e. Les intervalles pour lesquels la fonction diminue

    f. Les intervalles pour lesquels la fonction est constante

    g. Symétrie autour de n'importe quel axe et/ou de l'origine

    h. Si la fonction est paire, impaire ou aucune

    28)

    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une relation circulaire, avec x interceptions à (-1, 0) et (1, 0) et y interceptions à (0, 1) et (0, -1).

    (29)

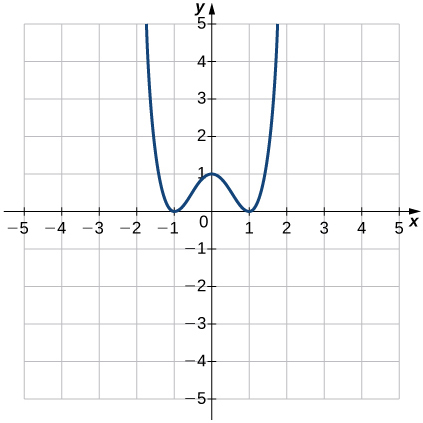
    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphe présente une relation incurvée. La relation diminue jusqu'à atteindre le point (-1, 0), puis augmente jusqu'à ce qu'elle atteigne le point (0, 1), puis diminue jusqu'à atteindre le point (1, 0), puis augmente à nouveau.

    Réponse
    Fonction ;
    a. Domaine : tous les nombres réels, plage :\(y≥0\)
    b.\(x=±1\)
    c.\(y=1\)
    d.\(−1<x<0\) et\(1<x<∞\)
    e.\(−∞<x<−1\) et\(0<x<1\)
    f. Non constant
    g. \(y\)-axe
    h. Even

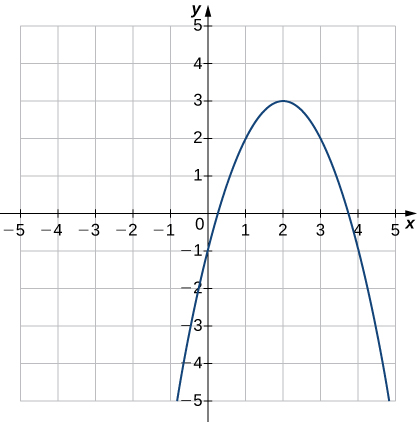
    (30)

    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une relation qui est une parabole. La relation courbe augmente jusqu'à atteindre le point (2, 3), puis commence à diminuer. Les interceptions x approximatives sont à (0,3, 0) et (3,7, 0) et l'intersection y est (-1, 0).

    31)

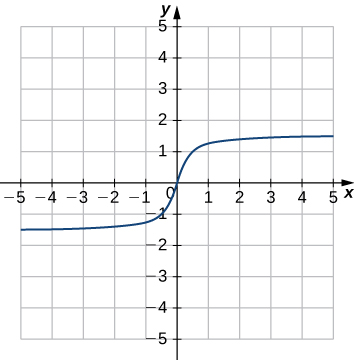
    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphe présente une relation incurvée. La relation courbe augmente tout au long du temps. L'intersection x et l'intersection y sont toutes deux à l'origine.

    Réponse
    Fonction ;
    a. Domaine : tous les nombres réels, plage :\(−1.5≤y≤1.5\)
    b.\(x=0\)
    c.\(y=0\)
    d. tous les nombres réels
    e. Aucun
    f. Non constant
    g. Origine
    h. Impaire

    32)

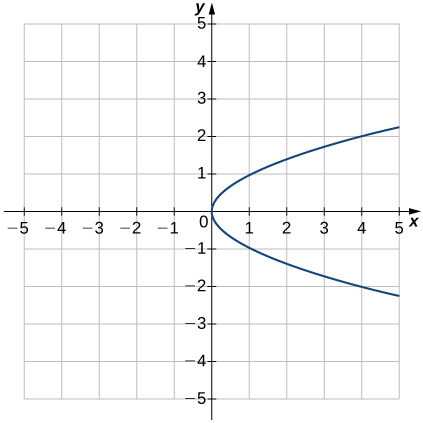
    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une relation qui est une parabole latérale s'ouvrant vers la droite. L'intersection x et l'intersection y se situent toutes deux à l'origine et la relation ne comporte aucun point à gauche de l'axe y. La relation inclut les points (1, -1) et (1, 1)

    33)

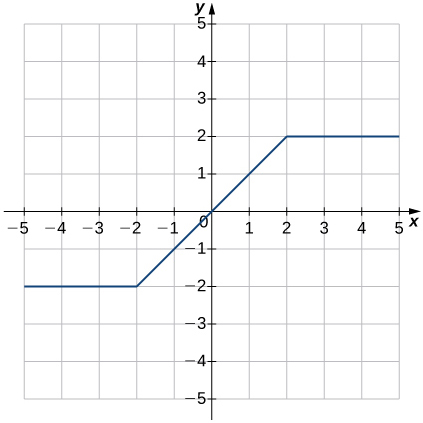
    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une relation qui est une ligne horizontale jusqu'au point (-2, -2), puis elle commence à augmenter en ligne droite jusqu'au point (2, 2). Après ces points, la relation redevient une ligne horizontale. L'intersection x et l'intersection y sont toutes deux à l'origine.

    Réponse
    Fonction ;
    a. Domaine :\(−∞<x<∞\), plage :\(−2≤y≤2\)
    b.\(x=0\)
    c.\(y=0\)
    d.\(−2<x<2\)
    e. Non décroissant
    f.\(−∞<x<−2\) et\(2<x<∞\)
    g. Origine
    h. Odd

    34)

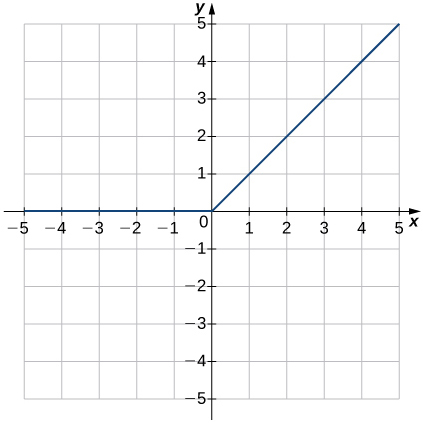
    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique représente une relation qui est une ligne horizontale jusqu'à l'origine, puis il commence à augmenter en ligne droite. L'intersection x et l'intersection y se situent toutes deux à l'origine et il n'y a aucun point en dessous de l'axe X.

    35)

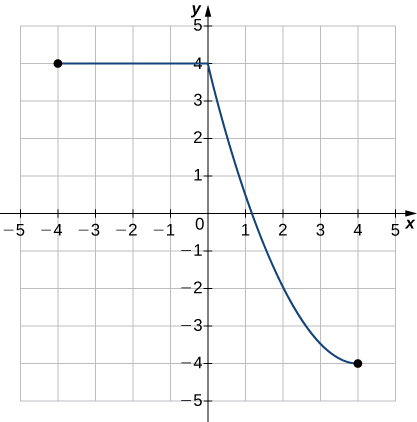
    Image d'un graphique. L'axe x va de -5 à 5 et l'axe y va de -5 à 5. Le graphique est une relation qui commence au point (-4, 4) et est une ligne horizontale jusqu'au point (0, 4), puis elle commence à décroître en ligne courbe jusqu'au point (4, -4), où le graphique se termine. L'intersection x est approximativement au point (1,2, 0) et l'intersection y est au point (0, 4).

    Réponse
    Fonction ;
    a. Domaine :\(−4≤x≤4\), plage :\(−4≤y≤4\)
    b.\(x=1.2\)
    c.\(y=4\)
    d. Sans augmentation
    e.\(0<x<4\)
    f.\(−4<x<0\)
    g. Aucune symétrie
    h. Ni

    Pour les exercices 36 à 41, pour chaque paire de fonctions, trouvez a.\(f+g\) b.\(f−g\) c.\(f⋅g\)\(f/g\) d. Déterminez le domaine de chacune de ces nouvelles fonctions.

    36)\(f(x)=3x+4,\quad g(x)=x−2\)

    (37)\(f(x)=x−8,\quad g(x)=5x^2\)

    Réponse
    a.\(5x^2+x−8\) ; tous les nombres réels
    b.\(−5x^2+x−8\) ; tous les nombres réels
    c.\(5x^3−40x^2\) ; tous les nombres réels
    d.\(\dfrac{x−8}{5x^2};\quad x≠0\)

    38)\(f(x)=3x^2+4x+1,\quad g(x)=x+1\)

    39)\(f(x)=9−x^2,\quad g(x)=x^2−2x−3\)

    Réponse
    a.\(−2x+6\) ; tous les nombres réels
    b.\(−2x^2+2x+12\) ; tous les nombres réels
    c.\(−x^4+2x^3+12x^2−18x−27\) ; tous les nombres réels
    d.\(−\dfrac{x+3}{x+1};\quad x≠−1,3\)

    40)\(f(x)=\sqrt{x},\quad g(x)=x−2\)

    41)\(f(x)=6+\dfrac{1}{x},\quad g(x)=\dfrac{1}{x}\)

    Réponse

    un.\(6+\dfrac{2}{x};\quad x≠0\)

    b.\(6; \quad x≠0\)

    c.\(6x+\dfrac{1}{x^2};\quad x≠0\)

    d.\(6x+1;\quad x≠0\)

    Pour les exercices 42 à 48, pour chaque paire de fonctions, trouvez a.\((f∘g)(x)\) et b.\((g∘f)(x)\) Simplifiez les résultats. Trouvez le domaine de chacun des résultats.

    42)\(f(x)=3x,\quad g(x)=x+5\)

    43)\(f(x)=x+4,\quad g(x)=4x−1\)

    Réponse
    a.\(4x+3\) ; tous les nombres réels
    b.\(4x+15\) ; tous les nombres réels

    44)\(f(x)=2x+4,\quad g(x)=x^2−2\)

    45)\(f(x)=x^2+7,\quad g(x)=x^2−3\)

    Réponse
    a.\(x^4−6x^2+16\) ; tous les nombres réels
    b.\(x^4+14x^2+46\) ; tous les nombres réels

    46)\(f(x)=\sqrt{x}, \quad g(x)=x+9\)

    47)\(f(x)=\dfrac{3}{2x+1},\quad g(x)=\dfrac{2}{x}\)

    Réponse

    un.\(\dfrac{3x}{4+x};\quad x≠0,−4\)

    b.\(\dfrac{4x+2}{3};\quad x≠−\frac{1}{2}\)

    48)\(f(x)=|x+1|,\quad g(x)=x^2+x−4\)

    49) Le tableau ci-dessous répertorie les vainqueurs du championnat NBA pour les années 2001 à 2012.

    Année Gagnant
    2001 Los Angeles Lakers
    2002 Los Angeles Lakers
    2003 San Antonio Spurs
    2004 Detroit Pistons
    2005 San Antonio Spurs
    2006 Heat de Miami
    2007 San Antonio Spurs
    2008 Celtics de Boston
    2009 Los Angeles Lakers
    2010 Los Angeles Lakers
    2011 Dallas Mavericks
    2012 Heat de Miami

    a. Examinez la relation dans laquelle les valeurs de domaine se situent entre 2001 et 2012 et où la plage est le gagnant correspondant. Cette relation est-elle une fonction ? Expliquez pourquoi ou pourquoi pas.

    b. Examinez la relation dans laquelle les valeurs du domaine sont les gagnantes et la plage correspond aux années correspondantes. Cette relation est-elle une fonction ? Expliquez pourquoi ou pourquoi pas.

    Réponse
    a. Oui, car il n'y a qu'un seul gagnant par année.
    b. Non, car trois équipes ont gagné plus d'une fois entre 2001 et 2012.

    50) [T] L'aire\(A\) d'un carré dépend de la longueur du côté s.

    a. Ecrivez une fonction\(A(s)\) pour l'aire d'un carré.

    b. Trouvez et interprétez\(A(6.5)\).

    c. Trouvez l'approximation exacte et l'approximation à deux chiffres significatifs de la longueur des côtés d'un carré d'une surface de 56 unités carrées.

    51) [T] Le volume d'un cube dépend de la longueur des côtés\(s.\)

    a. Ecrivez une fonction\(V(s)\) pour l'aire d'un carré.

    b. Trouvez et interprétez\(V(11.8)\).

    Réponse
    a.\(V(s)=s^3\)
    b.\(V(11.8)≈1643\) ; un cube de 11,8 cm de côté a un volume d'environ 1 643 unités cubes.

    52) [L] Une société de location de voitures loue des voitures pour un montant fixe de 20$ et un tarif horaire de 10,25$. Par conséquent, le coût total\(C\) de la location d'une voiture est fonction du nombre d'heures pendant lesquelles\(t\) la voiture est louée et du forfait.

    a. Écrivez la formule de la fonction qui modélise cette situation.

    b. Trouvez le coût total de location d'une voiture pour 2 jours et 7 heures.

    c. Déterminez combien de temps la voiture a été louée si la facture est de 432,73$.

    53) [T] Un véhicule a un réservoir de 20 gallons et atteint 15 mi/gal. Le nombre de kilomètres\(N\) parcourus dépend de la quantité d'essence contenue\(x\) dans le réservoir.

    a. Rédigez une formule qui modélise cette situation.

    b. Déterminez le nombre de kilomètres que le véhicule peut parcourir (i) sur un réservoir plein et (ii) sur les 3/4 d'un réservoir d'essence.

    c. Déterminez le domaine et l'étendue de la fonction.

    d. Déterminez combien de fois la conductrice a dû s'arrêter pour prendre de l'essence si elle a parcouru un total de 578 miles.

    Réponse
    a.\(N(x)=15x\)
    b. i. Par conséquent\(N(20)=15(20)=300\), le véhicule peut parcourir 300 miles avec un réservoir d'essence plein.
    ii. \(N(15)=225\); par conséquent, le véhicule peut parcourir 225 miles sur les 3/4 d'un réservoir d'essence.
    c. Domaine :\(0≤x≤20\) ; autonomie :\([0,300]\)
    d. Le conducteur a dû s'arrêter au moins une fois, étant donné qu'il faut environ 39 gallons d'essence pour parcourir un total de 578 miles.

    54) [T] Le volume\(V\) d'une sphère dépend de la longueur de son rayon\(V=(4/3)πr^3\). Comme la Terre n'est pas une sphère parfaite, nous pouvons utiliser le rayon moyen pour mesurer du centre à sa surface. Le rayon moyen est la distance moyenne entre le centre physique et la surface, sur la base d'un grand nombre d'échantillons. Détermine le volume de la Terre avec un rayon moyen\(6.371×106\) m.

    55) [T] Une certaine bactérie pousse en culture dans une région circulaire. Le rayon du cercle, mesuré en centimètres, est donné par\(r(t)=6−\dfrac{5}{t^2+1}\), où\(t\) est le temps mesuré en heures depuis qu'un cercle d'un rayon de 1 cm de la bactérie a été introduit dans la culture.

    a. Exprime la surface de la bactérie en fonction du temps.

    b. Trouvez la zone exacte et approximative de la culture bactérienne en 3 heures.

    c. Exprime la circonférence des bactéries en fonction du temps.

    d. Déterminez la circonférence exacte et approximative de la bactérie en 3 heures.

    Réponse
    a.\(A(t)=A(r(t))=π⋅(6−\frac{5}{t^2+1})^2\)
    b. Exact :\(\frac{121π}{4}\) ; environ\(95\text{ cm}^2\)
    c.\(C(t)=C(r(t))=2π(6−\frac{5}{t^2+1})\)
    d. Exact :\(11π\) ; environ\(35\) cm

    56) [T] Un touriste américain visite Paris et doit convertir des dollars américains en euros, ce qui peut être fait à l'aide de la fonction\(E(x)=0.79x\), où\(x\) est le nombre de dollars américains et\(E(x)\) le nombre équivalent d'euros. Comme les taux de conversion fluctuent, lorsque le touriste revient aux États-Unis deux semaines plus tard, la conversion de l'euro en dollar américain se\(D(x)=1.245x\) fait comme suit : où\(x\) est le nombre d'euros et\(D(x)\) est le nombre équivalent de dollars américains.

    a. Trouvez la fonction composite qui convertit directement des dollars américains en dollars américains via l'euro. Ce touriste a-t-il perdu de la valeur lors du processus de conversion ?

    b. Utilisez (a) pour déterminer combien de dollars américains la touriste récupérerait à la fin de son voyage si elle convertissait 200 dollars supplémentaires à son arrivée à Paris.

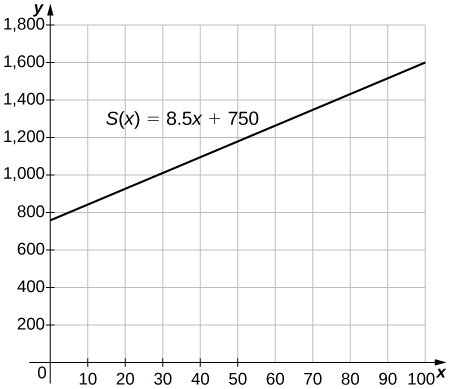
    57) [T] Le gérant d'un magasin de skateboard verse à ses employés un salaire mensuel\(S\) de 750$ plus une commission de 8,50$ pour chaque planche à roulettes qu'ils vendent.

    a. Rédigez une fonction\(y=S(x)\) qui modélise le salaire mensuel d'un travailleur en fonction du nombre de planches à roulettes qu'\(x\)il vend.

    b. Trouvez le salaire mensuel approximatif lorsqu'un travailleur vend 25, 40 ou 55 planches à roulettes.

    c. Utilisez la fonction INTERSECT d'une calculatrice graphique pour déterminer le nombre de planches à roulettes qui doivent être vendues pour qu'un travailleur gagne un revenu mensuel de 1 400$. (Conseil : trouvez l'intersection de la fonction et de la ligne\(y=1400\).)

    Image d'un graphique. L'axe y va de 0 à 1800 et l'axe x va de 0 à 100. Le graphique représente la fonction « S (x) = 8,5 x + 750 », qui est une droite croissante. La fonction a une intersection y à (0, 750) et l'intersection x n'est pas affichée.

    Réponse
    a.\(S(x)=8.5x+750\) b. 962,50$, 1090$, 1217,50$ c. 77 planches à roulettes

    58) [T] Utilisez une calculatrice graphique pour représenter graphiquement le demi-cercle\(y=\sqrt{25−(x−4)^2}\). Utilisez ensuite la fonction INTERCEPT pour trouver la valeur des intercepts\(x\) - et\(y\) -intercepts.

    Image d'un graphique. L'axe y va de -6 à 6 et l'axe x va de -1 à 10. Le graphique représente la fonction qui est un demi-cercle (la moitié supérieure d'un cercle). La fonction commence au point (-1, 0), passe par le point (0, 3), possède un maximum au point (4, 5) et se termine au point (9, 0). Aucun de ces points n'est étiqueté, ils servent uniquement de référence.