1.1 : Révision des fonctions

Objectifs d'apprentissage

• Utilisez la notation fonctionnelle pour évaluer une fonction.
• Déterminez le domaine et la plage d'une fonction.
• Dessine le graphe d'une fonction.
• Trouvez les zéros d'une fonction.
• Reconnaissez une fonction à partir d'une table de valeurs.
• Créez de nouvelles fonctions à partir de deux fonctions données ou plus.
• Décrivez les propriétés de symétrie d'une fonction.

Dans cette section, nous fournissons une définition formelle d'une fonction et examinons plusieurs manières dont les fonctions sont représentées, notamment par le biais de tableaux, de formules et de graphiques. Nous étudions la notation formelle et les termes liés aux fonctions. Nous définissons également la composition des fonctions et les propriétés de symétrie. La plupart de ces documents seront une revue pour vous, mais ils constituent une référence pratique pour vous rappeler certaines des techniques algébriques utiles pour travailler avec des fonctions.

Fonctions

Étant donné deux ensembles\(A\) et\(B\) un ensemble avec des éléments qui sont des paires ordonnées,\((x,y)\) où\(x\) est un élément de\(A\) et\(y\) est un élément de\(B,\) est une relation de\(A\) à\(B\). Une relation de\(A\) à\(B\) définit une relation entre ces deux ensembles. Une fonction est un type de relation spécial dans lequel chaque élément du premier ensemble est lié à exactement un élément du second ensemble. L'élément du premier ensemble est appelé entrée ; l'élément du second ensemble est appelé sortie. Les fonctions sont constamment utilisées en mathématiques pour décrire les relations entre deux ensembles. Pour toute fonction, lorsque nous connaissons l'entrée, la sortie est déterminée, donc nous disons que la sortie est fonction de l'entrée. Par exemple, l'aire d'un carré est déterminée par la longueur de son côté. Nous disons donc que la surface (la sortie) est fonction de la longueur de son côté (l'entrée). La vitesse d'une balle lancée en l'air peut être décrite comme une fonction du temps pendant lequel la balle est en l'air. Le coût de l'envoi d'un colis est fonction du poids du colis. Les fonctions ayant de nombreuses utilisations, il est important de disposer de définitions et d'une terminologie précises pour les étudier.

Figure\(\PageIndex{1}\) : Une fonction peut être visualisée en tant que périphérique d'entrée/sortie

Définition : Fonctions

Une fonction\(f\) se compose d'un ensemble d'entrées, d'un ensemble de sorties et d'une règle pour attribuer chaque entrée à exactement une sortie. L'ensemble des entrées est appelé le domaine de la fonction. L'ensemble des sorties est appelé plage de la fonction.

Figure\(\PageIndex{2}\) : Une fonction fait correspondre chaque élément du domaine à exactement un élément de la plage. Bien que chaque entrée ne puisse être envoyée que vers une seule sortie, deux entrées différentes peuvent être envoyées vers la même sortie.

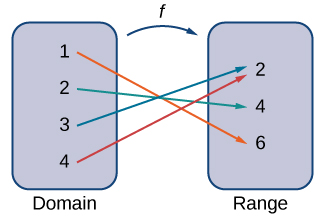
Par exemple, considérez la fonction\(f\), où le domaine est l'ensemble de tous les nombres réels et où la règle est de mettre les entrées au carré. Ensuite, l'entrée\(x=3\) est affectée à la sortie\(3^2=9\).

Comme chaque nombre réel non négatif possède une racine carrée de valeur réelle, chaque nombre non négatif est un élément de la plage de cette fonction. Comme il n'existe aucun nombre réel avec un carré négatif, les nombres réels négatifs ne sont pas des éléments de la plage. Nous concluons que l'intervalle est l'ensemble des nombres réels non négatifs.

Pour une fonction générale\(f\) avec domaine\(D\), nous utilisons souvent\(x\) pour désigner l'entrée et\(y\) la sortie associée à\(x\). Ce faisant, nous appelons la\(x\) variable indépendante et\(y\) la variable dépendante, car elle dépend de\(x\). En utilisant la notation des fonctions, nous écrivons\(y=f(x)\), et nous lisons cette équation comme «\(y\) égale à ».\(x.”\) Pour la fonction\(f\) de quadrature décrite précédemment, nous écrivons\(f(x)=x^2\).

Le concept d'une fonction peut être visualisé à l'aide de Figures\(\PageIndex{1}\) -\(\PageIndex{3}\).

Figure\(\PageIndex{3}\) : Dans ce cas, le graphe d'une fonction\(f\) possède un domaine\(\{1,2,3\}\) et une plage de\(\{1,2\}\). La variable indépendante est\(x\) et la variable dépendante est\(y\).

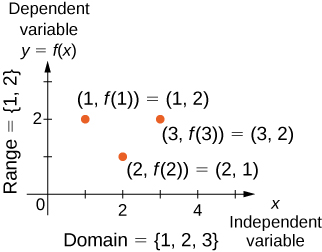
Nous pouvons également visualiser une fonction en traçant des points\((x,y)\) dans le plan de coordonnées où\(y=f(x)\). Le graphe d'une fonction est l'ensemble de tous ces points. Par exemple, considérez la fonction\(f\), où le domaine est l'ensemble\(D=\{1,2,3\}\) et la règle\(f(x)=3−x\). Dans la figure\(\PageIndex{4}\), nous tracons un graphique de cette fonction.

Figure\(\PageIndex{4}\) : Nous voyons ici un graphique de la fonction\(f\) avec domaine\(\{1,2,3\}\) et règle\(f(x)=3−x\). Le graphique comprend les points\((x,f(x))\) pour tous\(x\) les éléments du domaine.

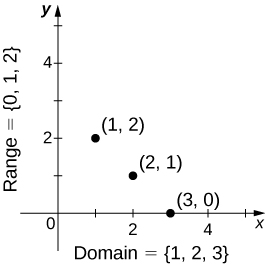
Chaque fonction possède un domaine. Cependant, une fonction est parfois décrite par une équation, comme dans\(f(x)=x^2\), sans domaine spécifique indiqué. Dans ce cas, le domaine est considéré comme l'ensemble de tous les nombres réels\(x\) pour lesquels\(f(x)\) il s'agit d'un nombre réel. Par exemple, comme n'importe quel nombre réel peut être carré, si aucun autre domaine n'est spécifié, nous considérons que le domaine\(f(x)=x^2\) de est l'ensemble de tous les nombres réels. D'autre part, la fonction de racine carrée\(f(x)=\sqrt{x}\) ne donne une sortie réelle que si elle n'\(x\)est pas négative. Par conséquent, le domaine de la fonction\(f(x)=\sqrt{x}\) est l'ensemble des nombres réels non négatifs, parfois appelé domaine naturel.

Pour les fonctions\(f(x)=x^2\) et les domaines\(f(x)=\sqrt{x}\), il s'agit d'ensembles comportant un nombre infini d'éléments. Nous ne pouvons évidemment pas énumérer tous ces éléments. Lorsque vous décrivez un ensemble avec un nombre infini d'éléments, il est souvent utile d'utiliser la notation setbuilder ou la notation par intervalles. Lorsque vous utilisez la notation set-builder pour décrire un sous-ensemble de tous les nombres réels, désignés\(R\), nous écrivons

\[\{x\,|\,\textit{x has some property}\}. \nonumber \]

Nous lisons cela comme l'ensemble de nombres\(x\) réels qui\(x\) possède une certaine propriété. Par exemple, si nous nous intéressons à l'ensemble des nombres réels supérieurs à un mais inférieurs à cinq, nous pourrions désigner cet ensemble en utilisant la notation set-builder en écrivant

\[\{x\,|\,1<x<5\}.\nonumber \]

Un ensemble tel que celui-ci, qui contient tous les nombres supérieurs\(a\) et inférieurs à,\(b,\) peut également être désigné à l'aide de la notation par intervalles\((a,b)\). Par conséquent,

\[(1,5)=\{x\,|\,1<x<5\}.\nonumber \]

Les nombres\(1\) et\(5\) sont appelés points de terminaison de cet ensemble. Si nous voulons considérer l'ensemble qui inclut les points de terminaison, nous désignerons cet ensemble en écrivant

\[[1,5]=\{x\,|\,1 \le x \le 5\}.\nonumber \]

Nous pouvons utiliser une notation similaire si nous voulons inclure l'un des points de terminaison, mais pas l'autre. Pour désigner l'ensemble des nombres réels non négatifs, nous utiliserions la notation set-builder

\[\{x\,|\,x\ge 0\}.\nonumber \]

Le plus petit nombre de cet ensemble est zéro, mais cet ensemble ne possède pas de plus grand nombre. En utilisant la notation par intervalles, nous utiliserions le symbole\(∞,\) qui fait référence à l'infini positif, et nous écririons l'ensemble comme

\[[0,∞)=\{x\,|\,x\ge 0\}.\nonumber \]

Il est important de noter qu'il ne\(∞\) s'agit pas d'un chiffre réel. Il est utilisé ici symboliquement pour indiquer que cet ensemble inclut tous les nombres réels supérieurs ou égaux à zéro. De même, si nous voulions décrire l'ensemble de tous les nombres non positifs, nous pourrions écrire

\[(−∞,0]=\{x\,|\,x≤0\}.\nonumber \]

Ici, la notation\(−∞\) fait référence à l'infini négatif, et elle indique que nous incluons tous les nombres inférieurs ou égaux à zéro, aussi petits soient-ils. L'ensemble

\[(−∞,∞)=\{\textit{x} \,|\, \textit{x is any real number}\}\nonumber \]

fait référence à l'ensemble de tous les nombres réels. Certaines fonctions sont définies à l'aide de différentes équations pour différentes parties de leur domaine. Ces types de fonctions sont appelés fonctions définies par morceaux. Par exemple, supposons que nous souhaitions définir une fonction\(f\) avec un domaine qui est l'ensemble de tous les nombres réels tels que\(f(x)=3x+1\) pour\(x≥2\) et\(f(x)=x^2\) pour\( x<2\). Nous désignons cette fonction en écrivant

\[f(x)=\begin{cases} 3x+1, & \text{if } x≥2 \\ x^2, & \text{if } x<2 \end{cases}\nonumber \]

Lors de l'évaluation de cette fonction pour une entrée\(x\), l'équation à utiliser dépend du fait que\(x≥2\) ou\(x<2\). Par exemple, puisque\(5>2\), nous utilisons le fait que\(f(x)=3x+1\) pour\(x≥2\) et que nous voyons cela\(f(5)=3(5)+1=16\). D'un autre côté, pour\(x=−1\), nous utilisons le fait que\(f(x)=x^2\) pour\(x<2\) et pour voir cela\(f(−1)=1\).

Exemple\(\PageIndex{1}\): Evaluating Functions

Pour la fonction\(f(x)=3x^2+2x−1\), évaluez :

1. \(f(−2)\)
2. \(f(\sqrt{2})\)
3. \(f(a+h)\)

Solution

Remplacez la valeur donnée\(x\) par dans la formule par\(f(x)\).

1. \(f(−2)=3(−2)^2+2(−2)−1=12−4−1=7\)
2. \(f(\sqrt{2})=3(\sqrt{2})^2+2\sqrt{2}−1=6+2\sqrt{2}−1=5+2\sqrt{2}\)
3. \(f(a+h)=3(a+h)^2+2(a+h)−1=3(a^2+2ah+h^2)+2a+2h−1=3a^2+6ah+3h^2+2a+2h−1\)

Exercice\(\PageIndex{1}\)

Pour\(f(x)=x^2−3x+5\), évaluer\(f(1)\) et\(f(a+h)\).

Allusion

Substituer\(1\) et\(a+h\) remplacer\(x\) dans la formule par\(f(x)\).

Réponse

\(f(1)=3 \)et\(f(a+h)=a^2+2ah+h^2−3a−3h+5\)

Exemple\(\PageIndex{2}\): Finding Domain and Range

Pour chacune des fonctions suivantes, déterminez le domaine i. et la plage ii.

1. \(f(x)=(x−4)^2+5\)
2. \(f(x)=\sqrt{3x+2}−1\)
3. \(f(x)=\dfrac{3}{x−2}\)

Solution

a. Considérez\(f(x)=(x−4)^2+5.\)

1. Comme\(f(x)=(x−4)^2+5\) il s'agit d'un nombre réel pour n'importe quel nombre réel\(x\), le domaine de\(f\) est l'intervalle\((−∞,∞)\).

2. Depuis\((x−4)^2≥0\), on le sait\(f(x)=(x−4)^2+5≥5\). Par conséquent, la plage doit être un sous-ensemble de\(\{y\,|\,y≥5\}.\) Pour montrer que chaque élément de cet ensemble se trouve dans la plage, nous devons montrer que pour un élément donné\(y\) dans cet ensemble, il existe un nombre réel\(x\) tel que\(f(x)=(x−4)^2+5=y\). En résolvant cette équation,\(x,\) nous voyons que nous avons besoin\(x\) de

\((x−4)^2=y−5.\)

Cette équation est satisfaite tant qu'il existe un nombre réel\(x\) tel que

\(x−4=±\sqrt{y−5}\)

Depuis\(y≥5\), la racine carrée est bien définie. Nous concluons que pour\(x=4±\sqrt{y−5},\)\(f(x)=y,\) et donc la gamme est\(\{y\,|\,y≥5 \}.\)

b. Considérez\(f(x)=\sqrt{3x+2}−1\).

1. Pour trouver le domaine de\(f\), nous avons besoin de l'expression\(3x+2≥0\). En résolvant cette inégalité, nous concluons que le domaine est\(\{x\,|\,x≥−2/3\}.\)

2. Pour connaître la gamme de\(f\), nous remarquons que depuis\(\sqrt{3x+2}≥0,\)\(f(x)=\sqrt{3x+2}−1≥−1\). Par conséquent, la plage de\(f\) doit être un sous-ensemble de l'ensemble\(\{y\,|\,y≥−1\}\). Pour montrer que chaque élément de cet ensemble se situe dans la plage de\(f\), nous devons montrer que pour tous les\(y\) éléments de cet ensemble, il existe un nombre réel\(x\) dans le domaine tel que\(f(x)=y.\) Let\(y≥−1.\) Then,\(f(x)=y\) si et seulement si

\(\sqrt{3x+2}−1=y.\)

Résoudre cette équation car\(x,\) nous voyons que cela\(x\) doit résoudre l'équation

\(\sqrt{3x+2}=y+1.\)

Depuis\(y≥−1\), un tel homme\(x\) pourrait exister. En mettant au carré les deux côtés de cette équation, nous avons\(3x+2=(y+1)^2.\)

Par conséquent, nous avons besoin

\(3x=(y+1)^2−2,\)

ce qui implique

\(x=\frac{1}{3}(y+1)^2−\frac{2}{3}.\)

Nous avons juste besoin de vérifier que cela\(x\) relève du domaine de\(f\). Puisque le domaine de\(f\) est composé de tous les nombres réels supérieurs ou égaux à\(\frac{−2}{3}\), et

\(\frac{1}{3}(y+1)^2-\frac{2}{3}≥−\frac{2}{3},\)

il existe un\(x\) dans le domaine de\(f\). Nous concluons que la gamme\(f\) est\(\{y\,|\,y≥−1\}.\)

c. Envisagez\(f(x)=\dfrac{3}{x−2}.\)

1. Comme il\(3/(x−2)\) est défini lorsque le dénominateur est différent de zéro, le domaine est\(\{x\,|\,x≠2\}.\)

2. Pour trouver la plage de,\(f,\) nous devons trouver les valeurs de\(y\) telle sorte qu'il existe un nombre réel\(x\) dans le domaine avec la propriété qui

\(\dfrac{3}{x−2}=y.\)

En résolvant cette équation,\(x,\) nous découvrons que

\(x=\dfrac{3}{y}+2.\)

Par conséquent\(y≠0\), tant qu'il existe un nombre réel\(x\) dans le domaine tel que\(f(x)=y\). Ainsi, la gamme est\(\{y\,|\,y≠0\}.\)

Exercice\(\PageIndex{2}\)

Trouvez le domaine et la gamme pour\(f(x)=\sqrt{4−2x}+5.\)

Allusion

Utiliser\(4−2x≥0\).

Réponse

Domaine =\(\{x\,|\,x≤2\}\) et plage =\(\{y\,|\,y≥5\}\)

Représenter des fonctions

Généralement, une fonction est représentée à l'aide d'un ou de plusieurs des outils suivants :

• Une table
• Un graphique
• Une formule

Nous pouvons identifier une fonction dans chaque formulaire, mais nous pouvons également les utiliser ensemble. Par exemple, nous pouvons tracer sur un graphique les valeurs d'un tableau ou créer un tableau à partir d'une formule.

Tables

Les fonctions décrites à l'aide d'un tableau de valeurs apparaissent fréquemment dans des applications réelles. Prenons l'exemple simple suivant. Nous pouvons décrire la température d'une journée donnée en fonction de l'heure de la journée. Supposons que nous enregistrons la température toutes les heures pendant une période de 24 heures à partir de minuit. Notre variable\(x\) d'entrée est le temps passé après minuit, mesuré en heures, et la variable\(y\) de sortie, la température des\(x\) heures après minuit, mesurée en degrés Fahrenheit. Nous enregistrons nos données dans le tableau\(\PageIndex{1}\).

Tableau\(\PageIndex{1}\) : Température en fonction de l'heure de la journée

Une heure après minuit	Température (°F)	Une heure après minuit	Température (°F)
0	58	12	84
1	54	13	85
2	53	14	85
3	52	15	83
4	52	16	82
5	55	17	80
6	60	18	77
7	64	19	74
8	72	20	69
9	75	21	65
10	78	22	60
11	80	23	58

Nous pouvons voir dans le tableau que la température est fonction du temps, et que la température diminue, puis augmente, puis diminue à nouveau. Cependant, nous ne pouvons pas obtenir une image claire du comportement de la fonction sans la représenter graphiquement.

Graphiques

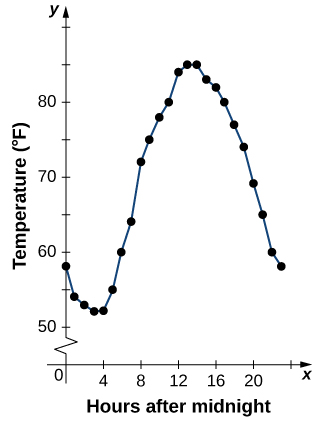
À partir d'une fonction\(f\) décrite par un tableau, nous pouvons fournir une image visuelle de la fonction sous forme de graphique. Le fait de représenter graphiquement les températures répertoriées dans le tableau\(\PageIndex{1}\) peut nous donner une meilleure idée de leur fluctuation au cours de la journée. La figure\(\PageIndex{5}\) montre le diagramme de la fonction de température.

Figure\(\PageIndex{5}\) : Le graphique des données du tableau\(\PageIndex{1}\) montre la température en fonction du temps.

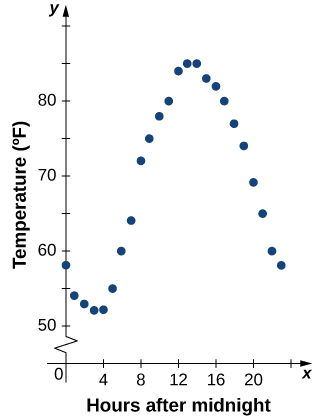
À partir des points tracés sur le graphique de la figure\(\PageIndex{5}\), nous pouvons visualiser la forme générale du graphique. Il est souvent utile de relier les points du graphique, qui représentent les données du tableau. Dans cet exemple, bien que nous ne puissions pas tirer de conclusion définitive concernant la température à tout moment pour lequel la température n'a pas été enregistrée, compte tenu du nombre de points de données collectés et de la tendance de ces points, il est raisonnable de soupçonner que les températures à d'autres moments ont suivi un modèle similaire, comme nous pouvons le voir sur la figure\(\PageIndex{6}\).

Figure\(\PageIndex{6}\) : Le fait de relier les points de la figure\(\PageIndex{5}\) montre le schéma général des données.

Formules algébriques

Parfois, on ne nous donne pas les valeurs d'une fonction sous forme de tableau, mais plutôt les valeurs dans une formule explicite. Les formules apparaissent dans de nombreuses applications. Par exemple, l'aire d'un cercle de rayon\(r\) est donnée par la formule\(A(r)=πr^2\). Lorsqu'un objet est projeté vers le haut depuis le sol avec une vitesse initiale\(v_{0}\) ft/s, sa hauteur au-dessus du sol entre le moment où il est projeté et celui où il touche le sol est donnée par la formule\(s(t)=−16t^2+v_{0}t\). Lorsque des\(P\) dollars sont investis dans un compte à un taux d'intérêt annuel\(r\) composé de façon continue, le montant d'argent après des\(t\) années est donné par la formule\(A(t)=Pe^{rt}\). Les formules algébriques sont des outils importants pour calculer les valeurs des fonctions. Souvent, nous représentons également ces fonctions visuellement sous forme de graphique.

Étant donné une formule algébrique pour une fonction\(f\), le graphe de\(f\) est l'ensemble des points\((x,f(x))\), où se\(x\) trouve dans le domaine de\(f\) et\(f(x)\) se trouve dans la plage. Pour représenter graphiquement une fonction donnée par une formule, il est utile de commencer par utiliser la formule pour créer un tableau des entrées et des sorties. Si le domaine de\(f\) est composé d'un nombre infini de valeurs, nous ne pouvons pas toutes les lister, mais comme la liste de certaines entrées et sorties peut être très utile, c'est souvent une bonne façon de commencer.

Lors de la création d'un tableau des entrées et des sorties, nous vérifions généralement si zéro est une sortie. Ces valeurs de «\(x\)\(f(x)=0\) where » sont appelées zéros d'une fonction. Par exemple, les zéros de\(f(x)=x^2−4\) sont\(x=±2\). Les zéros déterminent où le graphe de\(f\) croise l'\(x\)axe des, ce qui nous donne plus d'informations sur la forme du graphe de la fonction. Le graphe d'une fonction peut ne jamais croiser l'\(x\)axe -ou il peut se croiser plusieurs fois (voire un nombre infini) de fois.

Un autre point d'intérêt est le\(y\) -intercept, s'il existe. Le\(y\) -intercept est donné par\((0,f(0))\).

Comme une fonction possède exactement une sortie pour chaque entrée, le graphe d'une fonction ne peut avoir qu'une seule\(y\) intersection. S'il\(x=0\) est dans le domaine d'une fonction\(f,\), il\(f\) possède exactement un\(y\) -intercept. S'il n'\(x=0\)est pas dans le domaine de\(f,\), il n'\(f\)a pas de\(y\) -intercept. De même, pour tout nombre\(c,\) réel\(c\) compris dans le domaine de\(f\), il existe exactement une sortie\(f(c),\) et la ligne\(x=c\) coupe le graphe d'\(f\)une seule fois. En revanche, si ce n'\(c\)est pas dans le domaine de n'\(f,\)\(f(c)\)est pas défini et la droite\(x=c\) n'intersecte pas le graphe de\(f\). Cette propriété est résumée dans le test de la ligne verticale.

Test de ligne verticale

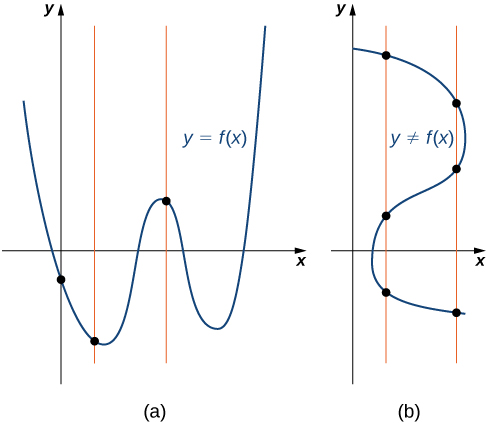
Pour une fonction donnée\(f\), chaque ligne verticale qui peut être tracée ne coupe\(f\) pas plus d'une fois le graphe. Si une ligne verticale coupe plusieurs fois un ensemble de points, l'ensemble de points ne représente pas une fonction.

Nous pouvons utiliser ce test pour déterminer si un ensemble de points tracés représente le graphe d'une fonction (Figure\(\PageIndex{7}\)).

Figure\(\PageIndex{7}\) : (a) L'ensemble des points tracés représente le graphe d'une fonction, car chaque ligne verticale coupe l'ensemble de points, au plus une fois. (b) L'ensemble de points tracés ne représente pas le graphe d'une fonction car certaines lignes verticales croisent l'ensemble de points plusieurs fois.

Exemple\(\PageIndex{3}\): Finding Zeros and \(y\)-Intercepts of a Function

Considérez la fonction\(f(x)=−4x+2.\)

1. Trouvez tous les zéros de\(f\).
2. Trouvez le\(y\) -intercept (le cas échéant).
3. Esquissez un graphique de\(f\).

Solution

1. Pour trouver les zéros, résolvez\(f(x)=−4x+2=0\). Nous découvrons qu'il y\(f\) a un zéro à\(x=1/2\).

2. Le\(y\) -intercept est donné par\((0,f(0))=(0,2).\)

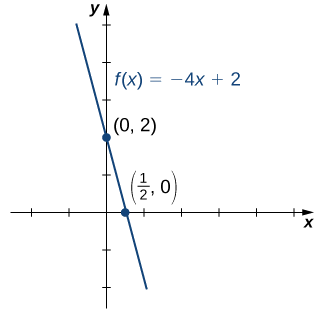
3. Étant donné qu'il\(f\) s'agit d'une fonction linéaire de la forme\(f(x)=mx+b\) qui passe par\((1/2,0)\) les points\((0,2)\), nous pouvons esquisser le graphique de\(f\) (Figure\(\PageIndex{8}\)).

Figure\(\PageIndex{8}\) : La fonction\(f(x)=−4x+2\) est une ligne avec\(x\) -intercept\((1/2,0)\) et\(y\) -intercept\((0,2)\).

Exemple\(\PageIndex{4}\): Using Zeros and \(y\)-Intercepts to Sketch a Graph

Considérez la fonction\(f(x)=\sqrt{x+3}+1\).

1. Trouvez tous les zéros de\(f\).
2. Trouvez le\(y\) -intercept (le cas échéant).
3. Esquissez un graphique de\(f\).

Solution

1. Pour trouver les zéros, résolvez\(\sqrt{x+3}+1=0\). Cette équation implique\(\sqrt{x+3}=−1\). Car\(\sqrt{x+3}≥0\) pour tous\(x\), cette équation n'a pas de solutions et ne\(f\) comporte donc pas de zéros.

2. Le\(y\) -intercept est donné par\((0,f(0))=(0,\sqrt{3}+1)\).

3. Pour représenter graphiquement cette fonction, nous créons un tableau de valeurs. Puisque nous avons besoin\(x+3≥0\), nous devons choisir des valeurs de\(x≥−3\). Nous choisissons des valeurs qui facilitent l'évaluation de la fonction racine carrée.

\(x\)	-3	-2	1
\(f(x)\)	1	2	3

En utilisant le tableau et en sachant que, puisque la fonction est une racine carrée, le graphe de\(f\) doit être similaire au graphe de\(y=\sqrt{x}\), nous esquissons le graphe (Figure\(\PageIndex{9}\)).

Figure\(\PageIndex{9}\) : Le graphique de\(f(x)=\sqrt{x+3}+1\) possède un\(y\) -intercepts mais pas de\(x\) -intercepts.

Exercice\(\PageIndex{4}\)

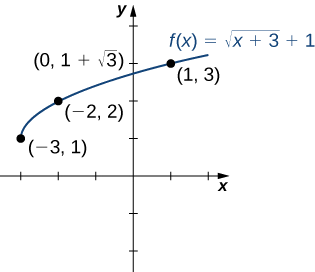
Trouvez les zéros de\(f(x)=x^3−5x^2+6x.\)

Allusion

Facturez le polynôme.

Réponse

\(x=0,2,3\)

Exemple\(\PageIndex{5}\): Finding the Height of a Free-Falling Object

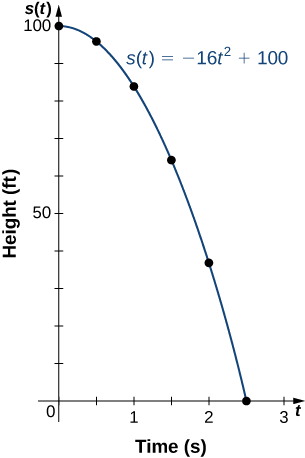
Si une balle est lâchée d'une hauteur de 100 pieds, sa hauteur s à la fois\(t\) est donnée par la fonction\(s(t)=−16t^2+100\), où s est mesuré en pieds et\(t\) en secondes. Le domaine est limité à l'intervalle\([0,c],\) où\(t=0\) est le moment où la balle est lâchée et\(t=c\) le moment où la balle touche le sol.

1. Créez un tableau indiquant la hauteur s (t) quand\(t=0,\, 0.5,\, 1,\, 1.5,\, 2,\) et\(2.5\). À l'aide des données de la table, déterminez le domaine de cette fonction. C'est-à-dire, trouvez l'heure à\(c\) laquelle la balle touche le sol.
2. Esquissez un graphique de\(s\).

Solution

\(t\)	0	0,5	1	1,5	2	2,5
\(s(t)\)	100	96	84	64	36	0

Puisque la balle touche le sol quand\(t=2.5\), le domaine de cette fonction est l'intervalle\([0,2.5]\).

2.

Figure\(\PageIndex{8}\), les valeurs de\(f(x)\) diminuent au fur et à mesure\(x\) qu'elles augmentent. Une fonction possédant cette propriété est dite décroissante. D'autre part, pour la fonction\(f(x)=\sqrt{x+3}+1\) illustrée dans la figure\(\PageIndex{9}\), les valeurs de\(f(x)\) augmentent à mesure que les valeurs de\(x\) augmentent. Une fonction dotée de cette propriété est dite croissante. Il est toutefois important de noter qu'une fonction peut augmenter sur un ou plusieurs intervalles et diminuer sur un ou plusieurs intervalles différents. Par exemple, en utilisant notre fonction de température tracée ci-dessus, nous pouvons voir que la fonction diminue sur l'intervalle\((0,4)\), augmente sur l'intervalle\((4,14)\), puis diminue sur l'intervalle\((14,23)\). Nous précisons l'idée d'une fonction augmentant ou diminuant sur un intervalle donné dans la définition suivante.

Définition : Augmenter et diminuer sur un intervalle

Nous disons qu'une fonction\(f\) augmente sur l'intervalle\(I\) si pour tous\(x_{1},\, x_{2}∈I,\)

\(f(x_{1})≤f(x_{2})\)quand\(x_{1}<x_{2}.\)

Nous disons qu'\(f\)il augmente strictement sur l'intervalle,\(I\) si c'est pour tous\(x_{1},x_{2}∈I,\)

\(f(x_{1})<f(x_{2})\)quand\(x_{1}<x_{2}.\)

Nous disons qu'une fonction\(f\) décroît sur l'intervalle\(I\) si pour tous\(x_{1},x_{2}∈I,\)

\(f(x_{1})≥f(x_{2})\)si\(x_{1}<x_{2}.\)

Nous disons qu'une fonction\(f\) est strictement décroissante sur l'intervalle\(I\) si pour tous\(x_{1},x_{2}∈I\),

\(f(x_{1})>f(x_{2})\)si\(x_{1}<x_{2}.\)

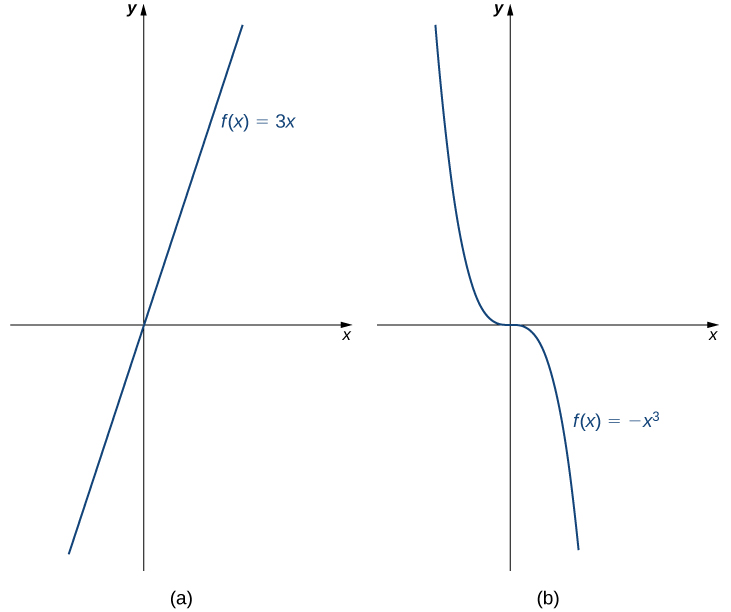
Par exemple, la fonction\(f(x)=3x\) augmente sur l'intervalle\((−∞,∞)\) car à\(3x_{1}<3x_{2}\) chaque fois\(x_{1}<x_{2}\). D'autre part, la fonction\(f(x)=−x^3\) diminue sur l'intervalle\((−∞,∞)\) car à\(−x^3_{1}>−x^3_{2}\) chaque fois\(x_{1}<x_{2}\) (Figure\(\PageIndex{10}\)).

Figure\(\PageIndex{10}\) : (a) La fonction\(f(x)=3x\) augmente sur l'intervalle\((−∞,∞)\). (b) La fonction\(f(x)=−x^3\) décroît sur l'intervalle\((−∞,∞)\).

Combinaison de fonctions

Maintenant que nous avons passé en revue les caractéristiques de base des fonctions, nous pouvons voir ce qu'il advient de ces propriétés lorsque nous combinons des fonctions de différentes manières, en utilisant des opérations mathématiques de base pour créer de nouvelles fonctions. Par exemple, si le coût de fabrication d'\(x\)articles pour une entreprise est décrit par la fonction\(C(x)\) et que les recettes générées par la vente d'\(x\)articles sont décrites par la fonction\(R(x)\), alors le bénéfice sur la fabrication et la vente des\(x\) articles est défini comme\(P(x)=R(x)−C(x)\). En utilisant la différence entre deux fonctions, nous avons créé une nouvelle fonction.

Nous pouvons également créer une nouvelle fonction en composant deux fonctions. Par exemple, étant donné les fonctions\(f(x)=x^2\) et\(g(x)=3x+1\), la fonction composite\(f∘g\) est définie de telle sorte que

\[(f∘g)(x)=f(g(x))=(g(x))^2=(3x+1)^2. \nonumber \]

La fonction composite\(g∘f\) est définie de telle sorte que

\[(g∘f)(x)=g(f(x))=3f(x)+1=3x^2+1. \nonumber \]

Notez que ces deux nouvelles fonctions sont différentes l'une de l'autre.

Combinaison de fonctions avec des opérateurs mathématiques

Pour combiner des fonctions à l'aide d'opérateurs mathématiques, il suffit d'écrire les fonctions avec l'opérateur et de les simplifier. Avec deux fonctions\(f\)\(g\), nous pouvons définir quatre nouvelles fonctions :

\((f+g)(x)=f(x)+g(x)\)	Somme
\((f−g)(x)=f(x)−g(x)\)	Différence
\((f·g)(x)=f(x)g(x)\)	Produit
\((\frac{f}{g})(x)=\frac{f(x)}{g(x)}\)pour\(g(x)≠0\)	Quotient

Exemple\(\PageIndex{6}\): Combining Functions Using Mathematical Operations

À partir des fonctions\(f(x)=2x−3\) et\(g(x)=x^2−1\), recherchez chacune des fonctions suivantes et indiquez son domaine.

1. \((f+g)(x)\)
2. \((f−g)(x)\)
3. \((f·g)(x)\)
4. \(\left(\dfrac{f}{g}\right)(x)\)

Solution

1. \((f+g)(x)=(2x−3)+(x^2−1)=x^2+2x−4.\)

Le domaine de cette fonction est l'intervalle\((−∞,∞)\).

2. \((f−g)(x)=(2x−3)−(x^2−1)=−x^2+2x−2.\)

Le domaine de cette fonction est l'intervalle\((−∞,∞)\).

3. \((f·g)(x)=(2x−3)(x^2−1)=2x^3−3x^2−2x+3.\)

Le domaine de cette fonction est l'intervalle\((−∞,∞)\).

4. \(\left(\dfrac{f}{g}\right)(x)=\dfrac{2x−3}{x^2−1}\).

Le domaine de cette fonction est\(\{x\,|\,x≠±1\}.\)

Exercice\(\PageIndex{6}\)

Pour\(f(x)=x^2+3\) et\(g(x)=2x−5\), trouvez\((f/g)(x)\) et indiquez son domaine.

Allusion

La nouvelle fonction\((f/g)(x)\) est un quotient de deux fonctions. Pour quelles valeurs de\(x\) est le dénominateur zéro ?

Réponse

\(\left(\dfrac{f}{g}\right)(x)=\frac{x^2+3}{2x−5}.\)Le domaine est\(\{x\,|\,x≠\frac{5}{2}\}.\)

Composition de la fonction

Lorsque nous composons des fonctions, nous prenons une fonction d'une fonction. Supposons, par exemple, que\(T\) la température d'un jour donné soit décrite en fonction du temps\(t\) (mesurée en heures après minuit), comme dans le tableau\(\PageIndex{1}\). Supposons que le coût\(C\), pour chauffer ou refroidir un bâtiment pendant 1 heure, puisse être décrit en fonction de la température\(T\). En combinant ces deux fonctions, nous pouvons décrire le coût du chauffage ou de la climatisation d'un bâtiment en fonction du temps en évaluant\(C(T(t))\). Nous avons défini une nouvelle fonction, désignée\(C∘T\), qui est définie de telle sorte que\((C∘T)(t)=C(T(t))\) pour tous\(t\) dans le domaine de\(T\). Cette nouvelle fonction est appelée fonction composite. Nous remarquons que puisque le coût est fonction de la température et que la température est fonction du temps, il est logique de définir cette nouvelle fonction\((C∘T)(t)\). Cela n'a aucun sens à prendre en compte\((T∘C)(t)\), car la température n'est pas fonction du coût.

Définition : Fonctions composites

Considérez la fonction\(f\) avec domaine\(A\) et plage\(B\), et la fonction\(g\) avec domaine\(D\) et plage\(E\). Si\(B\) est un sous-ensemble de\(D\), alors la fonction composite\((g∘f)(x)\) est la fonction dont le domaine est\(A\) tel que

\[(g∘f)(x)=g(f(x)) \nonumber \]

Une fonction composite\(g∘f\) peut être visualisée en deux étapes. Tout d'abord, la fonction\(f\) mappe chaque entrée\(x\) du domaine de\(f\) à sa sortie\(f(x)\) dans la plage de\(f\). Deuxièmement, étant donné que la plage de\(f\) est un sous-ensemble du domaine de\(g\), la sortie\(f(x)\) est un élément du domaine de\(g\), et elle est donc mappée à une sortie située\(g(f(x))\) dans la plage de\(g\). Dans la figure\(\PageIndex{11}\), nous voyons une image visuelle d'une fonction composite.

Figure\(\PageIndex{11}\) : Pour la fonction composite\(g∘f\), nous avons\((g∘f)(1)=4,\)\((g∘f)(2)=5,\) et\((g∘f)(3)=4\).

Exemple\(\PageIndex{7}\): Compositions of Functions Defined by Formulas

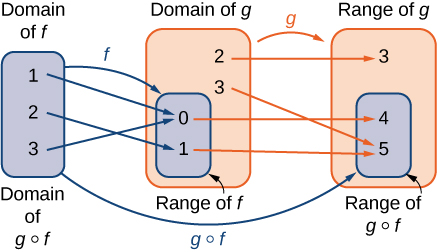
Tenez compte des fonctions\(f(x)=x^2+1\) et\(g(x)=1/x\).

1. Trouvez\((g∘f)(x)\) et indiquez son domaine et sa gamme.
2. Évaluer\((g∘f)(4),\)\((g∘f)(−1/2)\).
3. Trouvez\((f∘g)(x)\) et indiquez son domaine et sa gamme.
4. Évaluer\((f∘g)(4),\)\((f∘g)(−1/2)\).

Solution

1. Nous pouvons trouver la formule de deux\((g∘f)(x)\) manières différentes. Nous pourrions écrire

\((g∘f)(x)=g(f(x))=g(x^2+1)=\dfrac{1}{x^2+1}\).

Sinon, nous pourrions écrire

\((g∘f)(x)=g(f(x))=\dfrac{1}{f(x)}=\dfrac{1}{x^2+1}.\)

Puisque\(x^2+1≠0\) pour tous les nombres réels,\(x,\) le domaine de\((g∘f)(x)\) est l'ensemble de tous les nombres réels. Depuis\(0<1/(x^2+1)≤1\), la plage est, tout au plus, l'intervalle\((0,1]\). Pour montrer que la plage correspond à la totalité de cet intervalle, nous allons\(y=1/(x^2+1)\) résoudre cette équation pour\(x\) montrer que pour tout ce qui se trouve\(y\) dans l'intervalle\((0,1]\), il existe un nombre réel\(x\) tel que\(y=1/(x^2+1)\). En résolvant cette équation,\(x,\) nous voyons que\(x^2+1=1/y\), ce qui implique que

\(x=±\sqrt{\frac{1}{y}−1}\)

Si\(y\) c'est dans l'intervalle\((0,1]\), l'expression sous le radical n'est pas négative, et il existe donc un nombre réel\(x\) tel que\(1/(x^2+1)=y\). Nous concluons que la plage de\(g∘f\) est l'intervalle\((0,1].\)

2. \((g∘f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}\)

\((g∘f)(−\frac{1}{2})=g(f(−\frac{1}{2}))=g((−\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}\)

3. Nous pouvons trouver une formule\((f∘g)(x)\) de deux manières. Tout d'abord, nous pourrions écrire

\((f∘g)(x)=f(g(x))=f(\frac{1}{x})=(\frac{1}{x})^2+1.\)

Sinon, nous pourrions écrire

\((f∘g)(x)=f(g(x))=(g(x))^2+1=(\frac{1}{x})^2+1.\)

Le domaine de\(f∘g\) est l'ensemble de tous les nombres réels\(x\) tels que\(x≠0\). Pour trouver la plage de,\(f,\) nous devons trouver toutes les valeurs\(y\) pour lesquelles il existe un nombre réel\(x≠0\) tel que

\(\left(\dfrac{1}{x}\right)^2+1=y.\)

Résoudre cette équation\(x,\) car nous voyons que nous\(x\) devons satisfaire

\(\left(\dfrac{1}{x}\right)^2=y−1,\)

ce qui simplifie

\(\dfrac{1}{x}=±\sqrt{y−1}\)

Enfin, nous obtenons

\(x=±\dfrac{1}{\sqrt{y−1}}.\)

Puisque\(1/\sqrt{y−1}\) est un nombre réel si et seulement si\(y>1,\) la plage de\(f\) est définie\(\{y\,|\,y≥1\}.\)

4. \((f∘g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}\)

\((f∘g)(−\frac{1}{2})=f(g(−\frac{1}{2}))=f(−2)=(−2)^2+1=5\)

Dans l'exemple\(\PageIndex{7}\), nous pouvons le voir\((f∘g)(x)≠(g∘f)(x)\). Cela nous indique, en termes généraux, que l'ordre dans lequel nous composons les fonctions est important.

Exercice\(\PageIndex{7}\)

Laissez\(f(x)=2−5x\). Laissez\(g(x)=\sqrt{x}.\) trouver\((f∘g)(x)\).

Solution

\((f∘g)(x)=2−5\sqrt{x}.\)

Exemple\(\PageIndex{8}\): Composition of Functions Defined by Tables

Examinez\(f\) les fonctions\(g\) décrites par

\(x\)	-3	-2	-1	0	1	2	3	4
\(f(x)\)	0	4	2	4	-2	0	-2	4

\(x\)	-4	-2	0	2	4
\(g(x)\)	1	0	3	0	5

1. Évaluer\((g∘f)(3)\),\((g∘f)(0)\).
2. Indiquez le domaine et la portée de\((g∘f)(x)\).
3. Évaluer\((f∘f)(3)\),\((f∘f)(1)\).
4. Indiquez le domaine et la portée de\((f∘f)(x)\).

Solution :

1. \((g∘f)(3)=g(f(3))=g(−2)=0\)

\((g∘f)(0)=g(4)=5\)

2. Le domaine de\(g∘f\) est l'ensemble\(\{−3,−2,−1,0,1,2,3,4\}.\) Puisque la plage de\(f\) est l'ensemble,\(\{−2,0,2,4\},\) la plage de\(g∘f\) est l'ensemble\(\{0,3,5\}.\)

3. \((f∘f)(3)=f(f(3))=f(−2)=4\)

\((f∘f)(1)=f(f(1))=f(−2)=4\)

4. Le domaine de\(f∘f\) est l'ensemble\(\{−3,−2,−1,0,1,2,3,4\}.\) Puisque la plage de\(f\) est l'ensemble,\(\{−2,0,2,4\},\) la plage de\(f∘f\) est l'ensemble\(\{0,4\}.\)

Exemple\(\PageIndex{9}\): Application Involving a Composite Function

Un magasin annonce une vente de 20 % sur toutes ses marchandises. Caroline dispose d'un coupon qui lui donne droit à une réduction supplémentaire de 15 % sur tout article, y compris la marchandise en solde. Si Caroline décide d'acheter un article au prix initial de\(x\) dollars, combien finira-t-elle par payer si elle applique son coupon au prix de vente ? Résolvez ce problème à l'aide d'une fonction composite.

Solution

Puisque le prix de vente est inférieur de 20 % au prix initial, si un article est\(x\) en dollars, son prix de vente est indiqué par\(f(x)=0.80x\). Puisque le coupon donne droit à une réduction de 15 % sur le prix de n'importe quel article, s'il s'agit d'un article en\(y\) dollars, le prix, après application du coupon, est donné par g (y) =0,85 an. Par conséquent, si le prix est initialement\(x\) en dollars, son prix de vente le sera,\(f(x)=0.80x\) puis son prix final après le coupon sera\(g(f(x))=0.85(0.80x)=0.68x\).

Exercice\(\PageIndex{9}\)

Si les articles sont en solde avec 10 % de réduction sur leur prix initial et qu'un client dispose d'un coupon de réduction supplémentaire de 30 %, quel sera le prix final d'un article initialement en\(x\) dollars, après avoir appliqué le coupon au prix de vente ?

Allusion

Le prix de vente d'un article dont le prix initial est\(x\) en dollars est de\(f(x)=0.90x\). Le prix du coupon pour un article en\(y\) dollars est de\(g(y)=0.70y\).

Solution

\((g∘f)(x)=0.63x\)

Symétrie des fonctions

Les graphes de certaines fonctions possèdent des propriétés de symétrie qui nous aident à comprendre la fonction et la forme de son graphe. Par exemple, considérez la fonction\(f(x)=x^4−2x^2−3\) illustrée dans la figure\(\PageIndex{12a}\). Si nous prenons la partie de la courbe située à droite de l'\(y\)axe -et que nous la retournons par-dessus l'\(y\)axe, elle se trouve exactement au-dessus de la courbe, à gauche de l'\(y\)axe. Dans ce cas, nous disons que la fonction présente une symétrie par rapport à\(y\) l'axe. D'autre part, considérez la fonction\(f(x)=x^3−4x\) illustrée dans la figure\(\PageIndex{12b}\). Si nous prenons le graphique et que\(180°\) nous le faisons pivoter autour de l'origine, le nouveau graphique aura exactement la même apparence. Dans ce cas, nous disons que la fonction présente une symétrie par rapport à l'origine.

Figure\(\PageIndex{12}\) : (a) Un graphique symétrique par rapport à l'\(y\)axe. (b) Un graphique symétrique par rapport à l'origine.

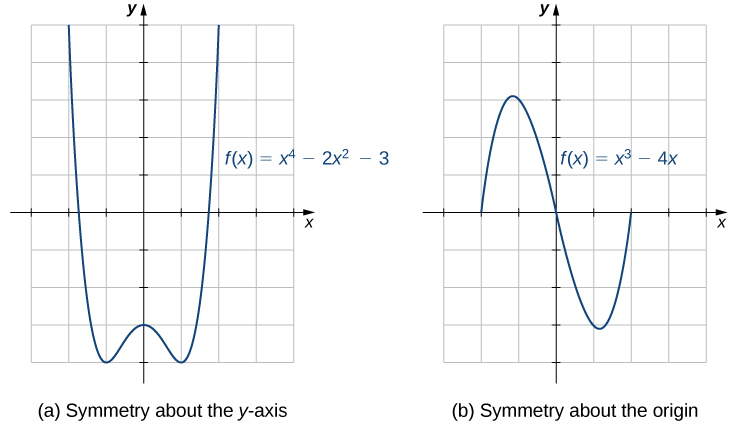
Si l'on nous donne le graphe d'une fonction, il est facile de voir si le graphe possède l'une de ces propriétés de symétrie. Mais sans graphique, comment déterminer algébriquement si une fonction\(f\) possède une symétrie ? En regardant à\(\PageIndex{12a}\) nouveau la figure, nous voyons que puisque\(f\) est symétrique par rapport à l'\(y\)axe Y, si le point\((x,y)\) se trouve sur le graphique,\((−x,y)\) il se trouve sur le graphique. En d'autres termes,\(f(−x)=f(x)\). Si une fonction\(f\) possède cette propriété, on dit qu'\(f\)il s'agit d'une fonction paire, qui présente une symétrie autour de\(y\) l'axe. Par exemple,\(f(x)=x^2\) c'est même parce que

\(f(−x)=(−x)^2=x^2=f(x).\)

En revanche, si vous regardez à\(\PageIndex{12b}\) nouveau la figure, si une fonction\(f\) est symétrique par rapport à l'origine, chaque fois que le point\((x,y)\) se trouve sur le graphique,\((−x,−y)\) il figure également sur le graphique. En d'autres termes,\(f(−x)=−f(x)\). Si\(f\) elle a cette propriété, nous disons que c'\(f\)est une fonction étrange, qui a une symétrie par rapport à l'origine. Par exemple,\(f(x)=x^3\) c'est étrange parce que

\(f(−x)=(−x)^3=−x^3=−f(x).\)

Définition : fonctions paires et impaires

• Si\(f(x)=f(−x)\) pour tout le monde est\(x\) dans le domaine de\(f\), alors\(f\) est une fonction paire. Une fonction paire est symétrique par rapport à l'\(y\)axe.
• Si\(f(−x)=−f(x)\) pour tout est\(x\) dans le domaine de\(f\), alors\(f\) est une fonction étrange. Une fonction étrange est symétrique par rapport à l'origine.

Exemple\(\PageIndex{10}\): Even and Odd Functions

Déterminez si chacune des fonctions suivantes est paire, impaire ou aucune.

1. \(f(x)=−5x^4+7x^2−2\)
2. \(f(x)=2x^5−4x+5\)
3. \(f(x)=\frac{3x}{x^2+1}\)

Solution

Pour déterminer si une fonction est paire ou impaire, nous l'évaluons\(f(−x)\) et la comparons à\(f(x)\) et\(−f(x)\).

1. \(f(−x)=−5(−x)^4+7(−x)^2−2=−5x^4+7x^2−2=f(x).\)Donc,\(f\) c'est égal.

2. \(f(−x)=2(−x)^5−4(−x)+5=−2x^5+4x+5.\)Maintenant, en\(f(−x)≠f(x).\) outre, en notant cela\(−f(x)=−2x^5+4x−5\), nous voyons que\(f(−x)≠−f(x)\). Par conséquent,\(f\) ce n'est ni pair ni étrange.

3. \(f(−x)=3(−x)/((−x)2+1)\)\(=−3x/(x^2+1)=\)\(−[3x/(x^2+1)]=−f(x).\)Par conséquent,\(f\) c'est étrange.

Exercice\(\PageIndex{10}\)

Déterminez s'il\(f(x)=4x^3−5x\) est pair, impair ou aucun des deux.

Allusion

Comparez\(f(−x)\) avec\(f(x)\) et\(−f(x)\).

Réponse

\(f(x)\)C'est étrange.

Une fonction symétrique qui apparaît fréquemment est la fonction de valeur absolue, écrite sous la forme\(|x|\). La fonction de valeur absolue est définie comme

\[f(x)=\begin{cases} -x, & \text{if }x<0 \\ x, & \text{if } x≥0 \end{cases} \nonumber \]

Certains élèves décrivent cette fonction en disant qu'elle « rend tout positif ». Par la définition de la fonction de valeur absolue, nous voyons que si\(x<0\), alors\(|x|=−x>0,\) et si\(x>0\), alors\(|x|=x>0.\) Cependant, pour\(x=0,\)\(|x|=0.\) Donc, il est plus précis de dire que pour toutes les entrées non nulles, la sortie est positive, mais si\(x=0\), la sortie\(|x|=0\). Nous concluons que la plage de la fonction de valeur absolue est\(\{y\,|\,y≥0\}.\) dans la figure\(\PageIndex{13}\), nous voyons que la fonction de valeur absolue est symétrique par rapport à l'\(y\)axe -et est donc une fonction paire.

Figure\(\PageIndex{13}\) : Le graphique de\(f(x)=|x|\) est symétrique par rapport à l'\(y\)axe.

Exemple\(\PageIndex{11}\): Working with the Absolute Value Function

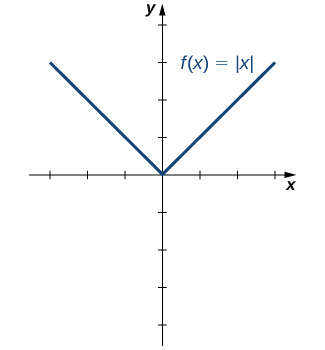
Déterminez le domaine et la plage de la fonction\(f(x)=2|x−3|+4\).

Solution

Puisque la fonction de valeur absolue est définie pour tous les nombres réels, le domaine de cette fonction est\((−∞,∞)\). Car\(|x−3|≥0\) pour tous\(x\), la fonction\(f(x)=2|x−3|+4≥4\). Par conséquent, la gamme est, tout au plus, l'ensemble\(\{y\,|\,y≥4\}.\) Pour voir que la gamme est, en fait, l'ensemble de cet ensemble, nous devons montrer qu'\(y≥4\)il existe un nombre réel\(x\) tel que

\(2|x−3|+4=y\)

Un nombre réel\(x\) satisfait cette équation tant que

\(|x−3|=\frac{1}{2}(y−4)\)

Puisque\(y≥4\), nous le savons\(y−4≥0\), le côté droit de l'équation n'est pas négatif, il est donc possible qu'il y ait une solution. En outre,

\(|x−3|=\begin{cases} −(x−3), & \text{if } x<3\\x−3, & \text{if } x≥3\end{cases}\)

Nous voyons donc qu'il existe deux solutions :

\(x=±\frac{1}{2}(y−4)+3\).

La plage de cette fonction est\(\{y\,|\,y≥4\}.\)

Exercice\(\PageIndex{11}\): Domain and Range

Pour la fonction\(f(x)=|x+2|−4\), recherchez le domaine et la plage.

Allusion

\(|x+2|≥0\)pour tous les nombres réels\(x\).

Réponse

Domaine =\((−∞,∞)\), plage =\(\{y\,|\,y≥−4\}.\)

Concepts clés

• Une fonction est un mappage entre un ensemble d'entrées et un ensemble de sorties avec exactement une sortie pour chaque entrée.
• Si aucun domaine n'est indiqué pour une fonction,\(y=f(x),\) le domaine est considéré comme l'ensemble de tous les nombres réels\(x\) pour lesquels la fonction est définie.
• Lorsque vous esquissez le graphe d'une fonction,\(f,\) chaque ligne verticale peut croiser le graphe, au plus une fois.
• Une fonction peut avoir n'importe quel nombre de zéros, mais elle possède au maximum un\(y\) -intercept.
• Pour définir la composition\(g∘f\), la plage de\(f\) doit être comprise dans le domaine de\(g\).
• Les fonctions paires sont symétriques par rapport à l'\(y\)axe -tandis que les fonctions impaires sont symétriques par rapport à l'origine.

Équations clés

• Composition de deux fonctions

\((g∘f)(x)=g\big(f(x)\big)\)

• Fonction de valeur absolue

\(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)

Lexique

fonction de valeur absolue

\(f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}\)

fonction composite

étant donné deux fonctions\(f\) et\(g\), une nouvelle fonction, désignée\(g∘f\), telle que\((g∘f)(x)=g(f(x))\)

décroissant sur l'intervalle\(I\)

une fonction décroissante sur l'intervalle\(I\) si, pour tout\(x_1,\,x_2∈I,\;f(x_1)≥f(x_2)\) si\(x_1<x_2\)

variable dépendante

la variable de sortie d'une fonction

domaine

l'ensemble des entrées pour une fonction

fonction uniforme

une fonction est paire si\(f(−x)=f(x)\) pour tous est\(x\) dans le domaine de\(f\)

fonction

un ensemble d'entrées, un ensemble de sorties et une règle pour mapper chaque entrée sur exactement une sortie

graphe d'une fonction

l'ensemble de points\((x,y)\) tel qu'il\(x\) se trouve dans le domaine de\(f\) et\(y=f(x)\)

augmentant sur l'intervalle\(I\)

une fonction augmentant sur l'intervalle\(I\) if for all\(x_1,\,x_2∈I,\;f(x_1)≤f(x_2)\) if\(x_1<x_2\)

variable indépendante

la variable d'entrée d'une fonction

fonction étrange

une fonction est étrange si elle est\(f(−x)=−f(x)\) pour toutes\(x\) dans le domaine de\(f\)

gamme

l'ensemble des sorties pour une fonction

symétrie par rapport à l'origine

le graphe d'une fonction\(f\) est symétrique par rapport à l'origine s'il\((−x,−y)\) se trouve sur le graphe ou à\(f\) chaque fois qu'\((x,y)\)il se trouve sur le graphique

symétrie autour de\(y\) l'axe

le graphe d'une fonction\(f\) est symétrique par rapport à l'\(y\)axe -s' il\((−x,y)\) se trouve sur le graphe ou\(f\) chaque fois qu'\((x,y)\)il se trouve sur le graphique

table de valeurs

un tableau contenant la liste des entrées et leurs sorties correspondantes

test de ligne verticale

étant donné le graphe d'une fonction, chaque ligne verticale croise le graphe, au plus une fois

zéros d'une fonction

lorsqu'un nombre réel\(x\) est le zéro d'une fonction\(f,\;f(x)=0\)