Chapitre 9 Exercices de révision
- Page ID
- 194464
Chapitre 9 Exercices de révision
Simplifiez et utilisez Square Roots
Simplifiez les expressions avec des racines
Dans les exercices suivants, simplifiez.
\(\sqrt{64}\)
\(\sqrt{144}\)
- Réponse
-
12
\(−\sqrt{25}\)
\(−\sqrt{81}\)
- Réponse
-
−9
\(\sqrt{−9}\)
\(\sqrt{−36}\)
- Réponse
-
ce n'est pas un vrai chiffre
\(\sqrt{64}+\sqrt{225}\)
\(\sqrt{64+225}\)
- Réponse
-
17
Dans les exercices suivants, estimez chaque racine carrée entre deux nombres entiers consécutifs.
\(\sqrt{28}\)
\(\sqrt{155}\)
- Réponse
-
\(12<\sqrt{155}<13\)
Racines carrés approximatives
Dans les exercices suivants, approximez chaque racine carrée et arrondissez à deux décimales.
\(\sqrt{15}\)
\(\sqrt{57}\)
- Réponse
-
7,55
Simplifier les expressions variables avec des racines car
Dans les exercices suivants, simplifiez.
\(\sqrt{q^2}\)
\(\sqrt{64b^2}\)
- Réponse
-
8b
\(−\sqrt{121a^2}\)
\(\sqrt{225m^{2}n^{2}}\)
- Réponse
-
15 mn
\(−\sqrt{100q^2}\)
\(\sqrt{49y^2}\)
- Réponse
-
7 ans
\(\sqrt{4a^{2}b^{2}}\)
\(\sqrt{121c^{2}d^{2}}\)
- Réponse
-
11 cd
Simplifiez les racines
Utilisez la propriété du produit pour simplifier les racines carrées
Dans les exercices suivants, simplifiez.
\(\sqrt{300}\)
\(\sqrt{98}\)
- Réponse
-
\(7\sqrt{2}\)
\(\sqrt{x^{13}}\)
\(\sqrt{y^{19}}\)
- Réponse
-
\(y^{9}\sqrt{y}\)
\(\sqrt{16m^4}\)
\(\sqrt{36n^{13}}\)
- Réponse
-
\(6n^{6}\sqrt{n}\)
\(\sqrt{288m^{21}}\)
\(\sqrt{150n^7}\)
- Réponse
-
\(5n^3\sqrt{6n}\)
\(\sqrt{48r^{5}s^{4}}\)
\(\sqrt{108r^{5}s^{3}}\)
- Réponse
-
\(6r^{2}s\sqrt{3rs}\)
\(\frac{10−\sqrt{50}}{5}\)
\(\frac{6+\sqrt{72}}{6}\)
- Réponse
-
\(1+\sqrt{2}\)
Dans les exercices suivants, simplifiez.
\(\sqrt{\frac{16}{25}}\)
\(\sqrt{\frac{81}{36}}\)
- Réponse
-
\(\frac{3}{2}\)
\(\sqrt{\frac{x^8}{x^4}}\)
\(\sqrt{\frac{y^6}{y^2}}\)
- Réponse
-
\(y^2\)
\(\sqrt{\frac{98p^6}{2p^2}}\)
\(\sqrt{\frac{72q^8}{2q^4}}\)
- Réponse
-
\(6q^2\)
\(\sqrt{\frac{65}{121}}\)
\(\sqrt{\frac{26}{169}}\)
- Réponse
-
\(\frac{\sqrt{26}}{13}\)
\(\sqrt{\frac{64x^4}{25x^2}}\)
\(\sqrt{\frac{36r^{10}}{16r^5}}\)
- Réponse
-
\(\frac{3r^2\sqrt{r}}{2}\)
\(\sqrt{\frac{48p^{3}q^{5}}{27pq}}\)
\(\sqrt{\frac{12r^{5}s^{7}}{75r^{2}s}}\)
- Réponse
-
\(\frac{2rs^3\sqrt{r}}{5}\)
Ajouter et soustraire des racines carrées
Ajouter et soustraire comme des racines carrées
Dans les exercices suivants, simplifiez.
\(3\sqrt{2}+\sqrt{2}\)
\(5\sqrt{5}+7\sqrt{5}\)
- Réponse
-
\(12\sqrt{5}\)
\(4\sqrt{y}+4\sqrt{y}\)
\(6\sqrt{m}−2\sqrt{m}\)
- Réponse
-
\(4\sqrt{m}\)
\(−3\sqrt{7}+2\sqrt{7}−\sqrt{7}\)
\(8\sqrt{13}+2\sqrt{3}+3\sqrt{13}\)
- Réponse
-
\(11\sqrt{13}+2\sqrt{3}\)
\(3\sqrt{5xy}−\sqrt{5xy}+3\sqrt{5xy}\)
\(2\sqrt{3rs}+\sqrt{3rs}−5\sqrt{rs}\)
- Réponse
-
\(3\sqrt{3rs}−5\sqrt{rs}\)
Ajouter et soustraire des racines carrées qui doivent être simplifiées
Dans les exercices suivants, simplifiez.
\(\sqrt{32}+3\sqrt{2}\)
\(\sqrt{8}+\sqrt{32}\)
- Réponse
-
\(5\sqrt{2}\)
\(\sqrt{72}+\sqrt{50}\)
\(\sqrt{48}+\sqrt{75}\)
- Réponse
-
\(9\sqrt{3}\)
\(3\sqrt{32}+\sqrt{98}\)
\(\frac{1}{3}\sqrt{27}−\frac{1}{8}\sqrt{192}\)
- Réponse
-
0
\(\sqrt{50y^5}−\sqrt{72y^5}\)
Ajoutez le texte des exercices ici.
- Réponse
-
\(17n^2\sqrt{2}\)
Multipliez les racines
Dans les exercices suivants, simplifiez.
\(\sqrt{2}·\sqrt{20}\)
\(2\sqrt{2}·6\sqrt{14}\)
- Réponse
-
\(24\sqrt{7}\)
\(\sqrt{2m^2}·\sqrt{20m^4}\)
\((\sqrt{62y})(\sqrt{350y^3})\)
- Réponse
-
\(180y^2\)
\((6\sqrt{3v^4})(5\sqrt{30v})\)
\((\sqrt{8})^2\)
- Réponse
-
8
\((−\sqrt{10})^2\)
\((2\sqrt{5})(5\sqrt{5})\)
- Réponse
-
50
\((−3\sqrt{3})(5\sqrt{18})\)
Dans les exercices suivants, simplifiez.
\(10(2−\sqrt{7})\)
- Réponse
-
\(20−10\sqrt{7}\)
\(\sqrt{3}(4+\sqrt{12})\)
\((5+\sqrt{2})(3−\sqrt{2})\)
- Réponse
-
\(13−2\sqrt{2}\)
\((5−3\sqrt{7})(1−2\sqrt{7})\)
\((1−3\sqrt{x})(5+2\sqrt{x})\)
- Réponse
-
\(5−13\sqrt{x}−6x\)
\((3+4\sqrt{y})(10−\sqrt{y})\)
\((1+6\sqrt{p})^2\)
- Réponse
-
\(1+12\sqrt{p}+36p\)
\((2−6\sqrt{5})^2\)
\((3+2\sqrt{7})(3−2\sqrt{7})\)
- Réponse
-
−19
\((6−\sqrt{11})(6+\sqrt{11})\)
Divisez les racines
Divisez les racines
Dans les exercices suivants, simplifiez.
\(\frac{\sqrt{75}}{10}\)
- Réponse
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{2−\sqrt{12}}{6}\)
\(\frac{\sqrt{48}}{\sqrt{27}}\)
- Réponse
-
\(\frac{4}{3}\)
\(\frac{\sqrt{75x^7}}{\sqrt{3x^3}}\)
\(\frac{\sqrt{20y^5}}{\sqrt{2y}}\)
- Réponse
-
\(y^2\sqrt{10}\)
\(\frac{\sqrt{98p^{6}q^{4}}}{\sqrt{2p^{4}q^{8}}}\)
Dans les exercices suivants, rationalisez le dénominateur.
\(\frac{10}{\sqrt{15}}\)
- Réponse
-
\(\frac{2\sqrt{15}}{3}\)
\(\frac{6}{\sqrt{6}}\)
\(\frac{5}{3\sqrt{5}}\)
- Réponse
-
\(\frac{\sqrt{5}}{3}\)
\(\frac{10}{2\sqrt{6}}\)
\(\sqrt{\frac{3}{28}}\)
- Réponse
-
\(\frac{\sqrt{21}}{14}\)
\(\sqrt{\frac{9}{75}}\)
Dans les exercices suivants, rationalisez le dénominateur.
\(\frac{4}{4+\sqrt{27}}\)
- Réponse
-
\(\frac{16−12\sqrt{3}}{−11}\)
\(\frac{5}{2−\sqrt{10}}\)
\(\frac{4}{2−\sqrt{5}}\)
- Réponse
-
\(−8−4\sqrt{5}\)
\(\frac{5}{4−\sqrt{8}}\)
\(\frac{\sqrt{2}}{\sqrt{p}+\sqrt{3}}\)
- Réponse
-
\(\frac{\sqrt{2p}−\sqrt{6}}{p−3}\)
\(\frac{\sqrt{x}−\sqrt{2}}{\sqrt{x}+\sqrt{2}}\)
Résoudre des équations avec des racines
Résoudre des équations
Dans les exercices suivants, résolvez l'équation.
\(\sqrt{7z+1}=6\)
- Réponse
-
5
\(\sqrt{4u−2}−4=0\)
\(\sqrt{6m+4}−5=0\)
- Réponse
-
\(\frac{7}{2}\)
\(\sqrt{2u−3}+2=0\)
\(\sqrt{u−4}+4=u\)
- Réponse
-
aucune solution
\(\sqrt{v−9}+9=0\)
\(\sqrt{r−4}−r=−10\)
- Réponse
-
13
\(\sqrt{s−9}−s=−9\)
\(2\sqrt{2x−7}−4=8\)
- Réponse
-
\(\frac{43}{2}\)
\(\sqrt{2−x}=\sqrt{2x−7}\)
\(\sqrt{a}+3=\sqrt{a+9}\)
- Réponse
-
0
\(\sqrt{r}+3=\sqrt{r+4}\)
\(\sqrt{u}+2=\sqrt{u+5}\)
- Réponse
-
\(\frac{11}{6}\)
\(\sqrt{n+11}−1=\sqrt{n+4}\)
\(\sqrt{y+5}+1=\sqrt{2y+3}\)
- Réponse
-
11
Dans les exercices suivants, résolvez. Arrondissez les approximations à une décimale.
Une palette de gazon couvrira une superficie d'environ 600 pieds carrés. Trinh veut commander une palette de gazon pour créer une pelouse carrée dans son jardin. Utilisez la formule\(s=\sqrt{A}\) pour déterminer la longueur de chaque côté de sa pelouse.
Un hélicoptère a largué un colis d'une hauteur de 900 pieds au-dessus d'un randonneur échoué. Utilisez la formule\(t=\frac{\sqrt{h}}{4}\) pour déterminer le nombre de secondes qu'il a fallu pour que le colis parvienne au randonneur.
- Réponse
-
7,5 secondes
L'agent Morales a mesuré les marques de dérapage de l'une des voitures impliquées dans un accident. La longueur des marques de dérapage était de 245 pieds. Utilisez la formule\(s=\sqrt{24d}\) pour déterminer la vitesse de la voiture avant que les freins ne soient serrés.
Racines supérieures
Simplifiez les expressions avec des racines
Dans les exercices suivants, simplifiez.
- \(\sqrt[6]{64}\)
- \(\sqrt[3]{64}\)
- Réponse
-
- 2
- 4
- \(\sqrt[3]{−27}\)
- \(\sqrt[4]{−64}\)
- \(\sqrt[9]{d^9}\)
- \(\sqrt[8]{v^8}\)
- Réponse
-
- d
- |v|
- \(\sqrt[5]{a^{10}}\)
- \(\sqrt[3]{b^{27}}\)
- \(\sqrt[4]{16x^8}\)
- \(\sqrt[6]{64y^{12}}\)
- Réponse
-
- \(2x^2\)
- \(2y^2\)
- \(\sqrt[7]{128r^{14}}\)
- \(\sqrt[4]{81s^{24}}\)
Utilisez la propriété Product pour simplifier les expressions ayant des racines plus élevées
Dans les exercices suivants, simplifiez.
- \(\sqrt[9]{d^9}\)
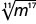
- Réponse
-
- d
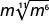
- \(\sqrt[3]{54}\)
- \(\sqrt[4]{128}\)
- \(\sqrt[5]{64c^8}\)
- \(\sqrt[4]{48d^7}\)
- Réponse
-
- \(2c\sqrt[5]{2c^3}\)
- \(2d\sqrt[4]{3d^3}\)
- \(\sqrt[3]{343q^7}\)
- \(\sqrt[6]{192r^9}\)
- \(\sqrt[3]{−500}\)
- \(\sqrt[4]{−16}\)
- Réponse
-
- \(−5\sqrt[3]{4}\)
- ce n'est pas un vrai chiffre
Dans les exercices suivants, simplifiez.
\(\sqrt[5]{\frac{r^{10}}{r^5}}\)
\(\sqrt[3]{\frac{w^{12}}{w^2}}\)
- Réponse
-
\(w^3\sqrt[3]{w}\)
\(\sqrt[4]{\frac{64y^8}{4y^5}}\)
\(\sqrt[3]{\frac{54z^9}{2z^3}}\)
- Réponse
-
\(3z^2\)
\(\sqrt[6]{\frac{64a^7}{b^2}}\)
Dans les exercices suivants, simplifiez.
\(4\sqrt[5]{20}−2\sqrt[5]{20}\)
- Réponse
-
\(2\sqrt[5]{20}\)
\(4\sqrt[3]{18}+3\sqrt[3]{18}\)
\(\sqrt[4]{1250}−\sqrt[4]{162}\)
- Réponse
-
\(2\sqrt[4]{2}\)
\(\sqrt[3]{640c^5}−\sqrt[3]{−80c^3}\)
\(\sqrt[5]{96t^8}+\sqrt[5]{486t^4}\)
- Réponse
-
\(2t^\sqrt[5]{3t^3}+3\sqrt[5]{2t^4}\)
Exposants rationnels
Simplifiez les expressions\(a^{\frac{1}{n}}\)
Dans les exercices suivants, écrivez comme une expression radicale.
\(r^{\frac{1}{8}}\)
\(s^{\frac{1}{10}}\)
- Réponse
-
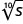
Dans les exercices suivants, écrivez avec un exposant rationnel.
\(\sqrt[5]{u}\)
\(\sqrt[6]{v}\)
- Réponse
-
\(v^{\frac{1}{6}}\)
\(\sqrt[3]{9m}\)
\(\sqrt[6]{10z}\)
- Réponse
-
\((10z)^{\frac{1}{6}}\)
Dans les exercices suivants, simplifiez.
\(16^{\frac{1}{4}}\)
\(32^{\frac{1}{5}}\)
- Réponse
-
2
\((−125)^{\frac{1}{3}}\)
\((125)^{−\frac{1}{3}}\)
- Réponse
-
\(\frac{1}{5}\)
\((−9)^{\frac{1}{2}}\)
\((36)^{−\frac{1}{2}}\)
- Réponse
-
\(\frac{1}{6}\)
Dans les exercices suivants, écrivez avec un exposant rationnel.
\(\sqrt[3]{q^5}\)
\(\sqrt[5]{n^8}\)
- Réponse
-
\(n^{\frac{8}{5}}\)
Dans les exercices suivants, simplifiez.
\(27^{−\frac{2}{3}}\)
\(64^{\frac{5}{2}}\)
- Réponse
-
32 768
\(36^{\frac{3}{2}}\)
\(81^{−\frac{5}{2}}\)
- Réponse
-
\(\frac{1}{59,049}\)
Utilisez les lois des exposants pour simplifier les expressions avec des exposants rationnels
Dans les exercices suivants, simplifiez.
\(3^{\frac{4}{5}}·3^{\frac{6}{5}}\)
\((x^6)^{\frac{4}{3}}\)
- Réponse
-
\(x^8\)
\(\frac{z^{\frac{5}{2}}}{z^{\frac{7}{5}}}\)
\((16s^{\frac{9}{4}})^{\frac{1}{4}}\)
- Réponse
-
\(2s^{\frac{9}{16}}\)
\((m^{8}n^{12})^{\frac{1}{4}}\)
\(\frac{z^{\frac{2}{3}}·z^{−\frac{1}{3}}}{z^{−\frac{5}{3}}}\)
- Réponse
-
\(z^2\)
Test d'entraînement
Dans les exercices suivants, simplifiez.
\(\sqrt{81+144}\)
\(\sqrt{169m^{4}n^{2}}\)
- Réponse
-
\(13m^{2}|n|\)
\(\sqrt{36n^{13}}\)
\(3\sqrt{13}+5\sqrt{2}+\sqrt{13}\)
- Réponse
-
\(4\sqrt{13}+5\sqrt{2}\)
\(5\sqrt{20}+2\sqrt{125}\)
\((3\sqrt{6y})(\sqrt{250y^3})\)
- Réponse
-
\(180y^2\sqrt{3}\)
\((2−5\sqrt{x})(3+\sqrt{x})\)
\((1−2\sqrt{q})^2\)
- Réponse
-
\(1−4\sqrt{q}+4q\)
- \(\sqrt{a^{12}}\)
- \(\sqrt[3]{b^{21}}\)
- \(\sqrt[4]{81x^{12}}\)
- \(\sqrt[6]{64y^{18}}\)
- Réponse
-
- \(3x^3\)
- \(2y^3\)
\(\sqrt[6]{\frac{64r^{12}}{25r^6}}\)
\(\sqrt{\frac{14y^3}{7y}}\)
- Réponse
-
\(y\sqrt{2}\)
\(\frac{\sqrt{256x^7}}{\sqrt{54x^2}}\)
\(\sqrt[4]{512}−2\sqrt[4]{32}\)
- Réponse
-
0
- \(256^{\frac{1}{4}}\)
- \(243^{\frac{1}{5}}\)
\(49^{\frac{3}{2}}\)
- Réponse
-
343
\(25^{−\frac{5}{2}}\)
\(\frac{w^{\frac{3}{4}}}{w^{\frac{7}{4}}}\)
- Réponse
-
\(\frac{1}{w}\)
\((27s^{\frac{3}{5}})^{\frac{1}{3}}\)
Dans les exercices suivants, rationalisez le dénominateur.
\(\frac{3}{2\sqrt{6}}\)
- Réponse
-
\(\frac{\sqrt{6}}{4}\)
\(\frac{\sqrt{3}}{\sqrt{x}+\sqrt{5}}\)
Dans les exercices suivants, résolvez.
\(3\sqrt{2x−3}−20=7\)
- Réponse
-
42
\(\sqrt{3u−2}=\sqrt{5u+1}\)
Dans l'exercice suivant, résolvez.
Un hélicoptère volant à une altitude de 600 pieds a largué un colis sur un canot de sauvetage. Utilisez la formule\(t=\frac{\sqrt{h}}{4}\) pour déterminer le nombre de secondes qu'il a fallu pour que le colis parvienne au randonneur. Arrondissez votre réponse au dixième de seconde le plus proche.
- Réponse
-
6,1 secondes


