Skip to main content
Global

9.8E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194517

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique permet de perfectionner

    Simplifiez les expressions\(a^{\frac{1}{n}}\)

    Dans les exercices suivants, écrivez comme une expression radicale.

    Exemple\(\PageIndex{47}\)
    1. \(x^{\frac{1}{2}}\)
    2. \(y^{\frac{1}{3}}\)
    3. \(z^{\frac{1}{4}}\)
    Exemple\(\PageIndex{48}\)
    1. \(r^{\frac{1}{2}}\)
    2. \(s^{\frac{1}{3}}\)
    3. \(t^{\frac{1}{4}}\)
    Réponse
    1. \(\sqrt{r}\)
    2. \(\sqrt[3]{s}\)
    3. \(\sqrt[4]{t}\)
    Exemple\(\PageIndex{49}\)
    1. \(u^{\frac{1}{5}}\)
    2. \(v^{\frac{1}{9}}\)
    3. \(w^{\frac{1}{20}}\)
    Exemple\(\PageIndex{50}\)
    1. \(g^{\frac{1}{7}}\)
    2. \(h^{\frac{1}{5}}\)
    3. \(j^{\frac{1}{25}}\)
    Réponse
    1. \(\sqrt[7]{g}\)
    2. \(\sqrt[5]{h}\)
    3. \(\sqrt[25]{j}\)
    Dans les exercices suivants, écrivez avec un exposant rationnel.
    Exemple\(\PageIndex{51}\)
    1. \(−\sqrt[7]{x}\)
    2. \(\sqrt[9]{y}\)
    3. \(\sqrt[5]{f}\)
    Exemple\(\PageIndex{52}\)
    1. \(\sqrt[8]{r}\)
    2. \(\sqrt[10]{s}\)
    3. \(\sqrt[4]{t}\)
    Réponse
    1. \(r^{\frac{1}{8}}\)
    2. \(s^{\frac{1}{10}}\)
    3. \(t^{\frac{1}{4}}\)
    Exemple\(\PageIndex{53}\)
    1. \ (\ sqrt [3] {a} \
    2. \(\sqrt[12]{b}\)
    3. \(\sqrt{c}\)
    Exemple\(\PageIndex{54}\)
    1. \(\sqrt[5]{u}\)
    2. \(\sqrt{v}\)

    .

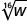
    Réponse
    1. \(u^{\frac{1}{5}}\)
    2. \(v^{\frac{1}{2}}\)
    3. \(w^{\frac{1}{16}}\)
    Exemple\(\PageIndex{55}\)
    1. \(\sqrt[3]{7c}\)
    2. \(\sqrt[7]{12d}\)
    3. \(3\sqrt[4]{5f}\)
    Exemple\(\PageIndex{56}\)
    1. \(\sqrt[4]{5x}\)
    2. \(\sqrt[8]{9y}\)
    3. \(7\sqrt[5]{3z}\)
    Réponse
    1. \((5x)^{\frac{1}{4}}\)
    2. \((9y)^{\frac{1}{8}}\)
    3. \(7(3z)^{\frac{1}{5}}\)
    Exemple\(\PageIndex{57}\)
    1. \(\sqrt{21p}\)
    2. \(\sqrt[4]{8q}\)
    3. \(\sqrt[6]{436r}\)
    Exemple\(\PageIndex{58}\)
    1. \(\sqrt[3]{25a}\)
    2. \(\sqrt{3b}\)

    .

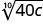
    Réponse
    1. \((25a)^{\frac{1}{3}}\)
    2. \((3b)^{\frac{1}{2}}\)
    3. \((40c)^{\frac{1}{10}}\)

    Dans les exercices suivants, simplifiez.

    Exemple\(\PageIndex{59}\)
    1. \(81^{\frac{1}{2}}\)
    2. \(125^{\frac{1}{3}}\)
    3. \(64^{\frac{1}{2}}\)
    Exemple\(\PageIndex{60}\)
    1. \(625^{\frac{1}{4}}\)
    2. \(243^{\frac{1}{5}}\)
    3. \(32^{\frac{1}{5}}\)
    Réponse
    1. 5
    2. 3
    3. 2
    Exemple\(\PageIndex{61}\)
    1. \(16^{\frac{1}{4}}\)
    2. \(16^{\frac{1}{2}}\)
    3. \(3125^{\frac{1}{5}}\)
    Exemple\(\PageIndex{62}\)
    1. \(216^{\frac{1}{3}}\)
    2. \(32^{\frac{1}{5}}\)
    3. \(81^{\frac{1}{4}}\)
    Réponse
    1. 6
    2. 2
    3. 3
    Exemple\(\PageIndex{63}\)
    1. \((−216)^{\frac{1}{3}}\)
    2. \(−216^{\frac{1}{3}}\)
    3. \((216)^{−\frac{1}{3}}\)
    Exemple\(\PageIndex{64}\)
    1. \((−243)^{\frac{1}{5}}\)
    2. \(−243^{\frac{1}{5}}\)
    3. \((243)^{−\frac{1}{5}}\)
    Réponse
    1. −3
    2. −3
    3. \(\frac{1}{3}\)
    Exemple\(\PageIndex{65}\)
    1. \((−1)^{\frac{1}{3}}\)
    2. \(−1^{\frac{1}{3}}\)
    3. \((1)^{−\frac{1}{3}}\)
    Exemple\(\PageIndex{66}\)
    1. \((−1000)^{\frac{1}{3}}\)
    2. \(−1000^{\frac{1}{3}}\)
    3. \((1000)^{−\frac{1}{3}}\)
    Réponse
    1. −10
    2. −10
    3. \ (\ frac {1} {10}
    Exemple\(\PageIndex{67}\)
    1. \((−81)^{\frac{1}{4}}\)
    2. \(−81^{\frac{1}{4}}\)
    3. \((81)^{−\frac{1}{4}}\)
    Exemple\(\PageIndex{68}\)
    1. \((−49)^{\frac{1}{2}}\)
    2. \(−49^{\frac{1}{2}}\)
    3. \((49)^{−\frac{1}{2}}\)
    Réponse
    1. ce n'est pas un vrai chiffre
    2. −7
    3. \(\frac{1}{7}\)
    Exemple\(\PageIndex{69}\)
    1. \((−36)^{\frac{1}{2}}\)
    2. \(−36^{\frac{1}{2}}\)
    3. \((36)^{−\frac{1}{2}}\)
    Exemple\(\PageIndex{70}\)
    1. \((−1)^{\frac{1}{4}}\)
    2. \((1)^{−\frac{1}{4}}\)
    3. \(−1^{\frac{1}{4}}\)
    Réponse
    1. ce n'est pas un vrai chiffre
    2. 1
    3. −1
    Exemple\(\PageIndex{71}\)
    1. \((−100)^{\frac{1}{2}}\)
    2. \(−100^{\frac{1}{2}}\)
    3. \((100)^{−\frac{1}{2}}\)
    Exemple\(\PageIndex{72}\)
    1. \((−32)^{\frac{1}{5}}\)
    2. \((243)^{−\frac{1}{5}}\)
    3. \(−125^{\frac{1}{3}}\)
    Réponse
    1. −2
    2. \(\frac{1}{3}\)
    3. −5

    Simplifiez les expressions\(a^{\frac{m}{n}}\)

    Dans les exercices suivants, écrivez avec un exposant rationnel.

    Exemple\(\PageIndex{73}\)
    1. \(\sqrt{m^5}\)
    2. \(\sqrt[3]{n^2}\)
    3. \(\sqrt[4]{p^3}\)
    Exemple\(\PageIndex{74}\)
    1. \(\sqrt[4]{r^7}\)
    2. \(\sqrt[5]{s^3}\)
    3. \(\sqrt[3]{t^7}\)
    Réponse
    1. \(r^{\frac{7}{4}}\)
    2. \(s^{\frac{3}{5}}\)
    3. \(t^{\frac{7}{3}}\)
    Exercice\(\PageIndex{75}\)
    1. \(\sqrt[5]{u^2}\)
    2. \(\sqrt[5]{v^8}\)
    3. \(\sqrt[9]{w^4}\)
    Exemple\(\PageIndex{76}\)
    1. \(\sqrt[3]{a}\)
    2. \(\sqrt[5]{b}\)
    3. \(\sqrt[3]{c^5}\)
    Réponse
    1. \(a^{\frac{1}{3}}\)
    2. \(b^{\frac{1}{5}}\)
    3. \(c^{\frac{5}{3}}\)
    Dans les exercices suivants, simplifiez.
    Exemple\(\PageIndex{77}\)
    1. \(16^{\frac{3}{2}}\)
    2. \(8^{\frac{2}{3}}\)
    3. \(10,000^{\frac{3}{4}}\)
    Exemple\(\PageIndex{78}\)
    1. \(1000^{\frac{2}{3}}\)
    2. \(25^{\frac{3}{2}}\)
    3. \(32^{\frac{3}{5}}\)
    Réponse
    1. 100
    2. 125
    3. 8
    Exemple\(\PageIndex{79}\)
    1. \(275^{\frac{3}{2}}\)
    2. \(16^{\frac{5}{4}}\)
    3. \(32^{\frac{2}{5}}\)
    Exemple\(\PageIndex{80}\)
    1. \(16^{\frac{3}{2}}\)
    2. \(125^{\frac{5}{3}}\)
    3. \(64^{\frac{4}{3}}\)
    Réponse
    1. 64
    2. 3125
    3. 256
    Exemple\(\PageIndex{81}\)
    1. \(32^{\frac{2}{5}}\)
    2. \(27^{−\frac{2}{3}}\)
    3. \(25^{−\frac{3}{2}}\)
    Exemple\(\PageIndex{82}\)
    1. \(64^{\frac{5}{2}}\)
    2. \(81^{−\frac{3}{2}}\)
    3. \(27^{−\frac{4}{3}}\)
    Réponse
    1. 32 768
    2. \(\frac{1}{729}\)
    3. \(\frac{1}{81}\)
    Exemple\(\PageIndex{83}\)
    1. \(25^{\frac{3}{2}}\)
    2. \(9^{−\frac{3}{2}}\)
    3. \((−64)^{\frac{2}{3}}\)
    Exemple\(\PageIndex{84}\)
    1. \(100^{\frac{3}{2}}\)
    2. \(49^{−\frac{5}{2}}\)
    3. \((−100)^{\frac{3}{2}}\)
    Réponse
    1. 1000
    2. \(\frac{1}{16,807}\)
    3. ce n'est pas un vrai numéro
    Exemple\(\PageIndex{85}\)
    1. \(−9^{\frac{3}{2}}\)
    2. \(−9^{−\frac{3}{2}}\)
    3. \((−9)^{\frac{3}{2}}\)
    Exemple\(\PageIndex{86}\)
    1. \(−64^{\frac{3}{2}}\)
    2. \(−64^{−\frac{3}{2}}\)
    3. \((−64)^{\frac{3}{2}}\)
    Réponse
    1. −512
    2. \(−\frac{1}{512}\)
    3. ce n'est pas un vrai chiffre
    Exemple\(\PageIndex{87}\)
    1. \(−100^{\frac{3}{2}}\)
    2. \(−100^{−\frac{3}{2}}\)
    3. \((−100)^{\frac{3}{2}}\)
    Exemple\(\PageIndex{88}\)
    1. \(−49^{\frac{3}{2}}\)
    2. \(−49^{−\frac{3}{2}}\)
    3. \((−49)^{\frac{3}{2}}\)
    Réponse
    1. −343
    2. \(−\frac{1}{343}\)
    3. ce n'est pas un vrai chiffre

    Utilisez les lois des exposants pour simplifier les expressions avec des exposants rationnels

    Dans les exercices suivants, simplifiez.

    Exemple\(\PageIndex{89}\)
    1. \(4^{\frac{5}{8}}·4^{\frac{11}{8}}\)
    2. \(m^{\frac{7}{12}}·m^{\frac{17}{12}}\)
    3. \(p^{\frac{3}{7}}·p^{\frac{18}{7}}\)
    Exemple\(\PageIndex{90}\)
    1. \(6^{\frac{5}{2}}·6^{\frac{12}{6}}\)
    2. \(n^{\frac{2}{10}}·n^{\frac{8}{10}}\)
    3. \(q^{\frac{2}{5}}·q^{\frac{13}{5}}\)
    Réponse
    1. 216
    2. n
    3. \(q^3\)
    Exemple\(\PageIndex{91}\)
    1. \(5^{\frac{1}{2}}·5^{\frac{7}{2}}\)
    2. \(c^{\frac{3}{4}}·c^{\frac{9}{4}}\)
    3. \(d^{\frac{3}{5}}·d^{\frac{2}{5}}\)
    Exemple\(\PageIndex{92}\)
    1. \(10^{\frac{1}{3}}·10^{\frac{5}{3}}\)
    2. \(x^{\frac{5}{6}}·x^{\frac{7}{6}}\)
    3. \(y^{\frac{11}{8}}·y^{\frac{21}{8}}\)
    Réponse
    1. 100
    2. \(x^2\)
    3. \(y^4\)
    Exemple\(\PageIndex{93}\)
    1. \((m^6)^{\frac{5}{2}}\)
    2. \((n^9)^{\frac{4}{3}}\)
    3. \((p^{12})^{\frac{3}{4}}\)
    Exemple\(\PageIndex{94}\)
    1. \((a^{12})^{\frac{1}{6}}\)
    2. \((b^{15})^{\frac{3}{5}}\)
    3. \((c^{11})^{\frac{1}{11}}\)
    Réponse
    1. \(a^2\)
    2. \(b^9\)
    3. c
    Exemple\(\PageIndex{95}\)
    1. \((x^{12})^{\frac{2}{3}}\)
    2. \((y^{20})^{\frac{2}{5}}\)
    3. \((z^{16})^{\frac{1}{16}}\)
    Exemple\(\PageIndex{96}\)
    1. \((h^6)^{\frac{4}{3}}\)
    2. \((k^{12})^{\frac{3}{4}}\)
    3. \((j^{10})^{\frac{7}{5}}\)
    Réponse
    1. \(h^8\)
    2. \(k^9\)
    3. \(j^{14}\)
    Exemple\(\PageIndex{97}\)
    1. \(\frac{x^{\frac{7}{2}}}{x^{\frac{5}{2}}}\)
    2. \(\frac{y^{\frac{5}{2}}}{y^{\frac{1}{2}}}\)
    3. \(\frac{r^{\frac{4}{5}}}{r^{\frac{9}{5}}}\)
    Exemple\(\PageIndex{98}\)
    1. \(\frac{s^{\frac{11}{5}}}{s^{\frac{6}{5}}}\)
    2. \(\frac{z^{\frac{7}{3}}}{z^{\frac{1}{3}}}\)
    3. \(\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}\)
    Réponse
    1. s
    2. \(z^2\)
    3. \(\frac{1}{w}\)
    Exemple\(\PageIndex{99}\)
    1. \(\frac{t^{\frac{12}{5}}}{t^{\frac{7}{5}}}\)
    2. \(\frac{x^{\frac{3}{2}}}{x^{\frac{1}{2}}}\)
    3. \(\frac{m^{\frac{13}{8}}}{m^{\frac{5}{8}}}\)
    Exemple\(\PageIndex{100}\)
    1. \(\frac{u^{\frac{13}{9}}}{u^{\frac{4}{9}}}\)
    2. \(\frac{r^{\frac{15}{7}}}{r^{\frac{8}{7}}}\)
    3. \(\frac{n^{\frac{3}{5}}}{n^{\frac{8}{5}}}\)
    Réponse
    1. u
    2. r
    3. \(\frac{1}{n}\)
    Exemple\(\PageIndex{101}\)
    1. \((9p^{\frac{2}{3}})^{\frac{5}{2}}\)
    2. \((27q^{\frac{3}{2}})^{\frac{4}{3}}\)
    Exemple\(\PageIndex{102}\)
    1. \((81r^{\frac{4}{5}})^{\frac{1}{4}}\)
    2. \((64s^{\frac{3}{7}})^{\frac{1}{6}}\)
    Réponse
    1. \(3r^{\frac{1}{5}}\)
    2. \(2s^{\frac{1}{14}}\)
    Exemple\(\PageIndex{103}\)
    1. \((16u^{\frac{1}{3}})^{\frac{3}{4}}\)
    2. \((100v^{\frac{2}{5}})^{\frac{3}{2}}\)
    Exemple\(\PageIndex{104}\)
    1. \((27m^{\frac{3}{4}})^{\frac{2}{3}}\)
    2. \((625n^{\frac{8}{3}})^{\frac{3}{4}}\)
    Réponse
    1. \(9m^{\frac{1}{2}}\)
    2. \(125n^2\)
    Exemple\(\PageIndex{105}\)
    1. \((x^{8}y^{10})^{\frac{1}{2}}\)
    2. \((a^{9}by ^{12})^{\frac{1}{3}}\)
    Exemple\(\PageIndex{106}\)
    1. \((r^{8}s^{4})^{\frac{1}{4}}\)
    2. \((u^{15}v^{20})^{\frac{1}{5}}\)
    Réponse
    1. \(r^{2}s\)
    2. \(u^{3}v^{4}\)
    Exemple\(\PageIndex{107}\)
    1. \((a^{6}b^{16})^{\frac{1}{2}}\)
    2. \((j^{9}k^{6})^{\frac{2}{3}}\)
    Exemple\(\PageIndex{108}\)
    1. \((r^{16}s^{10})^{\frac{1}{2}}\)
    2. \((u^{10}v^5)^{\frac{4}{5}}\)
    Réponse
    1. \(r^{8}s^{5}\)
    2. \(u^{8}v^{4}\)
    Exemple\(\PageIndex{109}\)
    1. \(\frac{r^{\frac{5}{2}}·r^{−\frac{1}{2}}}{r^{−\frac{3}{2}}}\)
    2. \(\frac{s^{\frac{1}{5}}·s}{s^{−\frac{9}{5}}}\)
    Exemple\(\PageIndex{110}\)
    1. \(\frac{a^{\frac{3}{4}}·a^{−\frac{1}{4}}}{a^{−\frac{10}{4}}}\)
    2. \(\frac{b^{\frac{2}{3}}·b}{b^{−\frac{7}{3}}}\)
    Réponse
    1. \(a^3\)
    2. \(b^4\)
    Exemple\(\PageIndex{111}\)
    1. \(\frac{c^{\frac{5}{3}}·c^{−\frac{1}{3}}}{c^{−\frac{2}{3}}}\)
    2. \(\frac{d^{\frac{3}{5}}·d}{d^{−\frac{2}{5}}}\)
    Exemple\(\PageIndex{112}\)
    1. \(\frac{m^{\frac{7}{4}}·m^{−\frac{5}{4}}}{m^{−\frac{2}{4}}}\)
    2. \(\frac{n^{\frac{3}{7}}·n}{n^{−\frac{4}{7}}}\)
    Réponse
    1. m
    2. \(n^2\)
    Exemple\(\PageIndex{113}\)

    \(4^{\frac{5}{2}}·4^{\frac{1}{2}}\)

    Exemple\(\PageIndex{114}\)

    \(n^{\frac{2}{6}}·n^{\frac{4}{6}}\)

    Réponse

    n

    Exemple\(\PageIndex{115}\)

    \((a^24)^ {\frac{1}{6}}\)

    Exemple\(\PageIndex{116}\)

    \((b^{10})^{\frac{3}{5}}\)

    Réponse

    \(b^6\)

    Exemple\(\PageIndex{117}\)

    \(\frac{w^{\frac{2}{5}}}{w^{\frac{7}{5}}}\)

    Exemple\(\PageIndex{118}\)

    \(\frac{z^{\frac{2}{3}}}{z^{\frac{8}{3}}}\)

    Réponse

    \(\frac{1}{z^2}\)

    Exemple\(\PageIndex{119}\)

    \((27r^{\frac{3}{5}})^{\frac{1}{3}}\)

    Exemple\(\PageIndex{120}\)

    \((64s^{\frac{3}{5}})^{\frac{1}{6}}\)

    Réponse

    \(2s^{\frac{1}{10}}\)

    Exemple\(\PageIndex{121}\)

    \((r^{9}s^{12})^{\frac{1}{3}}\)

    Exemple\(\PageIndex{122}\)

    \((u^{12}v^{18})^{\frac{1}{6}}\)

    Réponse

    \(u^{2}v^{3}\)

    Mathématiques quotidiennes

    Exemple\(\PageIndex{123}\)

    Aménagement paysager Joe veut avoir un terrain de jardin carré dans son jardin. Il dispose de suffisamment de compost pour couvrir une superficie de 144 pieds carrés. Simplifiez\(144^{\frac{1}{2}}\) pour trouver la longueur de chaque côté de son jardin.

    Exemple\(\PageIndex{124}\)

    Aménagement paysager Elliott veut créer un patio carré dans sa cour. Il dispose de suffisamment de béton pour paver une superficie de 242 pieds carrés. Simplifiez\(242^{\frac{1}{2}}\) pour trouver la longueur de chaque côté de son patio. Arrondissez au dixième de pied le plus proche.

    Réponse

    15,6 pieds

    Exemple\(\PageIndex{125}\)

    Gravité En installant des décorations de Noël, Bob a fait tomber une décoration du sommet d'un arbre de 12 pieds de haut. Simplifiez\(\frac{12^{\frac{1}{2}}}{16^{\frac{1}{2}}}\) pour savoir combien de secondes il a fallu pour que la décoration atteigne le sol. Arrondir au dixième de seconde le plus proche.

    Exemple\(\PageIndex{126}\)

    Gravité Un avion a largué une fusée éclairante d'une hauteur de 1 024 pieds au-dessus d'un lac. Simplifiez\(\frac{1024^{\frac{1}{2}}}{16^{\frac{1}{2}}}\) pour savoir combien de secondes il a fallu à la torche pour atteindre l'eau.

    Réponse

    8 secondes

    Exercices d'écriture

    Exemple\(\PageIndex{127}\)

    Montrez deux méthodes algébriques différentes pour simplifier\(4^{\frac{3}{2}}\). Expliquez toutes vos étapes.

    Exemple\(\PageIndex{128}\)

    Expliquez pourquoi l'expression\((−16)^{\frac{3}{2}}\) ne peut pas être évaluée.