9.5E : Exercices
- Page ID
- 194492
La pratique permet de perfectionner
Divisez les racines
Dans les exercices suivants, simplifiez.
\(\frac{\sqrt{27}}{6}\)
- Réponse
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{\sqrt{50}}{10}\)
\(\frac{\sqrt{72}}{9}\)
- Réponse
-
\(\frac{2\sqrt{2}}{3}\)
\(\frac{\sqrt{243}}{6}\)
\(\frac{2−\sqrt{32}}{8}\)
- Réponse
-
\(\frac{1−2\sqrt{2}}{4}\)
\(\frac{3+\sqrt{27}}{9}\)
\(\frac{6+\sqrt{45}}{6}\)
- Réponse
-
\(\frac{2+\sqrt{5}}{2}\)
\(\frac{10−\sqrt{200}}{20}\)
\(\frac{\sqrt{80}}{\sqrt{125}}\)
- Réponse
-
\(\frac{4}{5}\)
\(\frac{\sqrt{72}}{\sqrt{200}}\)
\(\frac{\sqrt{128}}{\sqrt{72}}\)
- Réponse
-
\(\frac{4}{3}\)
\(\frac{\sqrt{48}}{\sqrt{75}}\)
- \(\frac{\sqrt{8x^6}}{2x^2}\)
- \(\frac{\sqrt{200m^5}}{98m}\)
- Réponse
-
- \(2x^2\)
- \(\frac{10m^2}{7}\)
- \(\frac{\sqrt{10y^3}}{5y}\)
- \(\frac{\sqrt{108n^7}}{243n^3}\)
\(\frac{\sqrt{75r^3}}{108r}\)
- Réponse
-
\(\frac{5r}{6}\)
\(\frac{\sqrt{196q^5}}{484q}\)
\(\frac{\sqrt{108p^{5}q^{2}}}{\sqrt{34p^{3}q^{6}}}\)
- Réponse
-
\(\frac{3p\sqrt{102}}{17q^2}\)
\(\frac{\sqrt{98rs^{10}}}{\sqrt{2r^{3}s^{4}}}\)
\(\frac{\sqrt{320mn^{5}}}{\sqrt{45m^{7}n^{3}}}\)
- Réponse
-
\(\frac{8n}{3m^3}\)
\(\frac{\sqrt{810c^{3}d^{7}}}{\sqrt{1000c^{5}d}}\)
\(\frac{\sqrt{98}}{14}\)
- Réponse
-
\(\frac{\sqrt{2}}{2}\)
\(\frac{\sqrt{72}}{18}\)
\(\frac{5+\sqrt{125}}{15}\)
- Réponse
-
\(\frac{1+\sqrt{3}}{3}\)
\(\frac{6−\sqrt{45}}{12}\)
\(\frac{\sqrt{96}}{\sqrt{150}}\)
- Réponse
-
\(\frac{4}{5}\)
\(\frac{\sqrt{28}}{\sqrt{63}}\)
\(\frac{\sqrt{26y^7}}{2y}\)
- Réponse
-
\(y^3\sqrt{13}\)
\(\frac{\sqrt{15x^3}}{\sqrt{3x}}\)
Rationaliser un dénominateur à un terme
Dans les exercices suivants, simplifiez et rationalisez le dénominateur.
\(\frac{10}{\sqrt{6}}\)
- Réponse
-
\(\frac{5\sqrt{6}}{3}\)
\(\frac{8}{\sqrt{3}}\)
\(\frac{6}{\sqrt{7}}\)
- Réponse
-
\(\frac{6\sqrt{7}}{7}\)
\(\frac{4}{\sqrt{5}}\)
\(\frac{3}{\sqrt{13}}\)
- Réponse
-
\(\frac{3\sqrt{13}}{13}\)
\(\frac{10}{\sqrt{11}}\)
\(\frac{10}{3\sqrt{10}}\)
- Réponse
-
\(\frac{\sqrt{10}}{3}\)
\(\frac{2}{5\sqrt{2}}\)
\(\frac{4}{9\sqrt{5}}\)
- Réponse
-
\(\frac{4\sqrt{5}}{45}\)
\(\frac{9}{2\sqrt{7}}\)
\(−\frac{9}{2\sqrt{3}}\)
- Réponse
-
\(−\frac{3\sqrt{3}}{2}\)
\(−\frac{8}{3\sqrt{6}}\)
\(\sqrt{\frac{3}{20}}\)
- Réponse
-
\(\frac{\sqrt{15}}{10}\)
\(\sqrt{\frac{4}{27}}\)
\(\sqrt{\frac{7}{40}}\)
- Réponse
-
\(\frac{\sqrt{70}}{20}\)
\(\sqrt{\frac{8}{45}}\)
\(\sqrt{\frac{19}{175}}\)
- Réponse
-
\(\frac{\sqrt{133}}{35}\)
\(\sqrt{\frac{17}{192}}\)
Rationaliser un dénominateur à deux termes
Dans les exercices suivants, simplifiez en rationalisant le dénominateur.
- \(\frac{3}{3+\sqrt{11}}\)
- \(\frac{8}{1−\sqrt{5}}\)
- Réponse
-
- \(\frac{3(3−\sqrt{11})}{−2}\)
- \(−2(1+\sqrt{5})\)
- \(\frac{4}{4+\sqrt{7}}\)
- \(\frac{7}{2−\sqrt{6}}\)
- \(\frac{5}{5+\sqrt{6}}\)
- \(\frac{6}{3−\sqrt{7}}\)
- Réponse
-
- \(\frac{5(5−\sqrt{6})}{19}\)
- \(3(3+\sqrt{7})\)
- \(\frac{6}{6+\sqrt{5}}\)
- \(\frac{5}{4−\sqrt{11}}\)
\(\frac{\sqrt{3}}{\sqrt{m}−\sqrt{5}}\)
- Réponse
-
\(\frac{\sqrt{3}(\sqrt{m}+\sqrt{5})}{m−5}\)
\(\frac{\sqrt{5}}{\sqrt{n}−\sqrt{7}}\)
\(\frac{\sqrt{2}}{\sqrt{x}−\sqrt{6}}\)
- Réponse
-
\(\frac{\sqrt{2}(\sqrt{x}+\sqrt{3})}{x−6}\)
\(\frac{\sqrt{7}}{\sqrt{y}+\sqrt{3}}\)
\(\frac{\sqrt{r}+\sqrt{5}}{\sqrt{r}−\sqrt{5}}\)
- Réponse
-
\(\frac{(\sqrt{r}+\sqrt{5})^2}{r−5}\)
\(\frac{\sqrt{s}−\sqrt{6}}{\sqrt{s}+\sqrt{6}}\)
\(\frac{\sqrt{150x^{2}y^{6}}}{\sqrt{6x^{4}y^{2}}}\)
- Réponse
-
\(\frac{5y^2}{x}\)
\(\frac{\sqrt{80p^{3}q}}{\sqrt{5pq^{5}}}\)
\(\frac{15}{\sqrt{5}}\)
- Réponse
-
\(3\sqrt{5}\)
\(\frac{3}{5\sqrt{8}}\)
\(\sqrt{\frac{8}{54}}\)
- Réponse
-
\(\frac{2\sqrt{3}}{9}\)
\(\sqrt{\frac{12}{20}}\)
\(\frac{3}{5+\sqrt{5}}\)
- Réponse
-
\(\frac{3(5−\sqrt{5})}{20}\)
\(\frac{20}{4−\sqrt{3}}\)
\(\frac{\sqrt{2}}{\sqrt{x}−\sqrt{3}}\)
- Réponse
-
\(\frac{\sqrt{2}(\sqrt{x}+\sqrt{3})}{x−3}\)
\(\frac{\sqrt{5}}{\sqrt{y}−\sqrt{7}}\)
\(\frac{\sqrt{x}+\sqrt{8}}{\sqrt{x}−\sqrt{8}}\)
- Réponse
-
\(\frac{(\sqrt{x}+2\sqrt{2})^2}{x−8}\)
\(\frac{\sqrt{m}−\sqrt{3}}{\sqrt{m}+\sqrt{3}}\)
Mathématiques quotidiennes
Un kit de ravitaillement est largué d'un avion volant à une altitude de 250 pieds. Simplifiez\(\sqrt{\frac{250}{16}}\) pour déterminer le nombre de secondes nécessaires pour que le kit d'alimentation atteigne le sol.
- Réponse
-
\(\frac{5\sqrt{10}}{4}\)secondes
Une fusée éclairante est larguée dans l'océan par un avion volant à une altitude de 1 200 pieds. Simplifiez\(\sqrt{\frac{1200}{16}}\) pour déterminer le nombre de secondes nécessaires pour que la fusée éclairante atteigne l'océan.
Exercices d'écriture
- Simplifiez\(\sqrt{\frac{27}{3}}\) et expliquez toutes vos étapes.
- Simplifiez\(\sqrt{\frac{27}{5}}\) et expliquez toutes vos étapes.
- Pourquoi les deux méthodes de simplification des racines carrées sont-elles différentes ?
- Réponse
-
Les réponses peuvent varier.
- \(\frac{1}{\sqrt{2}}\)Approximation en divisant\(\frac{1}{1.414}\) en utilisant une division longue sans calculatrice.
- Rationaliser le dénominateur des\(\frac{1}{\sqrt{2}}\) dons\(\frac{\sqrt{2}}{2}\). \(\frac{\sqrt{2}}{2}\)Approximation en divisant\(\frac{1.414}{2}\) en utilisant une division longue sans calculatrice.
- Êtes-vous d'accord pour dire que la rationalisation du dénominateur facilite les calculs ? Pourquoi ou pourquoi pas ?
Auto-vérification
ⓐ Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.
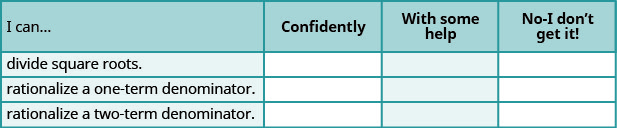
ⓑ Après avoir examiné la liste de contrôle, pensez-vous être bien préparé pour la section suivante ? Pourquoi ou pourquoi pas ?


