Skip to main content
Global

9.5 : Diviser les racines carrées

  1. Last updated
  2. Save as PDF
  • Page ID
    194478

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Divisez les racines
    • Rationaliser un dénominateur à un terme
    • Rationaliser un dénominateur à deux termes
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Trouvez une fraction équivalente à\(\frac{5}{8}\) avec le dénominateur 48.
      Si vous avez oublié ce problème, passez en revue l'exercice 1.6.1.
    2. Simplifiez :\((\sqrt{5})^2\).
      Si vous avez oublié ce problème, consultez l'exemple 9.4.13.
    3. Multipliez : (7+3x) (7−3x).
      Si vous avez oublié ce problème, passez en revue l'exercice 6.4.22.

    Divisez les racines

    Nous savons que l'on simplifie les fractions en supprimant les facteurs communs au numérateur et au dénominateur. Lorsque nous avons une fraction avec une racine carrée dans le numérateur, nous simplifions d'abord la racine carrée. Ensuite, nous pouvons rechercher des facteurs communs.

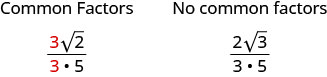
    Cette figure montre deux colonnes. Le premier est appelé « Facteurs communs » et a 3 fois la racine carrée de 2 sur 3 fois 5 en dessous. Les deux numéros trois sont rouges. La deuxième colonne est intitulée « Aucun facteur commun » et possède 2 fois la racine carrée de 3 sur 3 fois 5.

    Exemple\(\PageIndex{1}\)

    Simplifiez :\(\frac{\sqrt{54}}{6}\)

    Réponse
      \(\frac{\sqrt{54}}{6}\)
    Simplifiez le radical. \(\frac{\sqrt{9}·\sqrt{6}}{6}\)
    Simplifiez. \(\frac{3\sqrt{6}}{6}\)
    Supprimez les facteurs communs. \(\frac{3\sqrt{6}}{3·2}\)
    Simplifiez. \(\frac{\sqrt{6}}{2}\)
    Exemple\(\PageIndex{2}\)

    Simplifiez :\(\frac{\sqrt{32}}{8}\).

    Réponse

    \(\frac{\sqrt{2}}{2}\)

    Exemple\(\PageIndex{3}\)

    Simplifiez :\(\frac{\sqrt{75}}{15}\).

    Réponse

    \(\frac{\sqrt{3}}{3}\)

    Exemple\(\PageIndex{4}\)

    Simplifiez :\(\frac{6−\sqrt{24}}{12}\).

    Réponse
      \(\frac{6−\sqrt{24}}{12}\)
    Simplifiez le radical. \(\frac{6−\sqrt{4}·\sqrt{6}}{12}\)
    Simplifiez. \(\frac{6−2\sqrt{6}}{12}\)
    Facturez le facteur commun à partir du numérateur. \(\frac{2(3−\sqrt{6})}{12}\)
    Supprimez les facteurs communs. \(\frac{2(3−\sqrt{6})}{2·6}\)
    Simplifiez. \(\frac{3−\sqrt{6}}{6}\)
    Exemple\(\PageIndex{5}\)

    Simplifiez :\(\frac{8−\sqrt{40}}{10}\).

    Réponse

    \(\frac{4−\sqrt{10}}{5}\)

    Exemple\(\PageIndex{6}\)

    Simplifiez :\(\frac{10−\sqrt{75}}{20}\).

    Réponse

    \(\frac{5−\sqrt{3}}{4}\)

    Nous avons utilisé la propriété quotient des racines carrées pour simplifier les racines carrées des fractions. La propriété du quotient de Square Roots dit

    \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\),\(b \ne 0\).

    Parfois, nous aurons besoin d'utiliser la propriété quotient des racines carrées « à l'envers » pour simplifier une fraction avec des racines carrées.

    \(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\),\(b \ne 0\).

    Nous allons réécrire la propriété quotient de Square Roots afin de voir les deux côtés ensemble. N'oubliez pas : nous supposons que toutes les variables sont supérieures ou égales à zéro, de sorte que leurs racines carrées soient des nombres réels.

    Définition : PROPRIÉTÉ DU QUOTIENT DES RACINES CARRÉES

    Si a, b sont des nombres réels non négatifs et\(b \ne 0\), alors

    \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)et\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)

    Nous utiliserons la propriété quotient des racines carrées « à l'envers » lorsque la fraction par laquelle nous commençons est le quotient de deux racines carrées et qu'aucun des radicaux n'est un carré parfait. Lorsque nous écrivons la fraction dans une seule racine carrée, nous pouvons trouver des facteurs communs dans le numérateur et le dénominateur.

    Exemple\(\PageIndex{7}\)

    Simplifiez :\(\frac{\sqrt{27}}{\sqrt{75}}\)

    Réponse
      \(\frac{\sqrt{27}}{\sqrt{75}}\)
    Aucun des radicaux n'est un carré parfait, donc réécrivez en utilisant la propriété quotient de la racine carrée. \(\sqrt{\frac{27}{75}}\)
    Supprimez les facteurs communs du numérateur et du dénominateur. \(\sqrt{\frac{9}{25}}\)
    Simplifiez. \(\frac{3}{5}\)
    Exemple\(\PageIndex{8}\)

    Simplifiez :\(\frac{\sqrt{48}}{\sqrt{108}}\)

    Réponse

    \(\frac{2}{3}\)

    Exemple\(\PageIndex{9}\)

    Simplifiez :\(\frac{\sqrt{96}}{\sqrt{54}}\)

    Réponse

    \(\frac{4}{3}\)

    Nous utiliserons la propriété du quotient pour les exposants\(\frac{a^m}{a^n}=a^{m−n}\), lorsque nous avons des variables avec des exposants dans les radicandes.

    Exemple\(\PageIndex{10}\)

    Simplifiez :\(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)

    Réponse
      \(\frac{\sqrt{6y^5}}{\sqrt{2y}}\)
    Aucun des radicaux n'est un carré parfait, donc réécrivez en utilisant la propriété quotient de la racine carrée. \(\sqrt{\frac{6y^5}{2y}}\)
    Supprimez les facteurs communs du numérateur et du dénominateur. \(\sqrt{3y^4}\)
    Simplifiez. \(y^2\sqrt{3}\)
    Exemple\(\PageIndex{11}\)

    Simplifiez :\(\frac{\sqrt{12r^3}}{\sqrt{6r}}\).

    Réponse

    \(r\sqrt{2}\)

    Exemple\(\PageIndex{12}\)

    Simplifiez :\(\frac{\sqrt{14p^9}}{\sqrt{2p^5}}\)

    Réponse

    \(p^2\sqrt{7}\)

    Exemple\(\PageIndex{13}\)

    Simplifiez :\(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)

    Réponse
      \(\frac{\sqrt{72x^3}}{\sqrt{162x}}\)
    Réécrivez en utilisant la propriété quotient des racines carrées. \(\sqrt{\frac{72x^3}{162x}}\)
    Supprimez les facteurs courants. \(\sqrt{\frac{18·4·x^2·x}{18·9·x}}\)
    Simplifiez. \(\sqrt{\frac{4x^2}{9}}\)
    Simplifiez le radical. \(\frac{2x}{3}\)
    Exemple\(\PageIndex{14}\)

    Simplifiez :\(\frac{\sqrt{50s^3}}{\sqrt{128s}}\).

    Réponse

    \(\frac{5s}{8}\)

    Exemple\(\PageIndex{15}\)

    Simplifiez :\(\frac{\sqrt{75q^5}}{\sqrt{108q}}\).

    Réponse

    \(\frac{5q^2}{6}\)

    Exemple\(\PageIndex{16}\)

    Simplifiez :\(\frac{\sqrt{147ab^8}}{\sqrt{3a^3b^4}}\).

    Réponse
      \(\frac{\sqrt{147ab^8}}{\sqrt{3a^{3}b^{4}}}\)
    Réécrivez en utilisant la propriété quotient des racines carrées. \(\sqrt{\frac{147ab^8}{3a^{3}b^{4}}}\)
    Supprimez les facteurs courants. \ (\ sqrt {\ frac {49b^4} {a^2}} \
    Simplifiez le radical. \(\frac{7b^2}{a}\)
    Exemple\(\PageIndex{17}\)

    Simplifiez :\(\frac{\sqrt{162x^{10}y^{2}}}{\sqrt{2x^6y^6}}\).

    Réponse

    \(\frac{9x^2}{y^2}\)

    Exemple\(\PageIndex{18}\)

    Simplifiez :\(\frac{\sqrt{300m^{3}n^{7}}}{\sqrt{3m^{5}n}}\).

    Réponse

    \(\frac{10n^3}{m}\)

    Rationaliser un dénominateur à un terme

    Avant que le calculateur ne devienne un outil de la vie quotidienne, les tableaux de racines carrées étaient utilisés pour trouver des valeurs approximatives des racines carrées. La figure montre une partie d'un tableau de carrés et de racines carrées. Les racines carrées sont estimées à cinq décimales environ dans ce tableau.

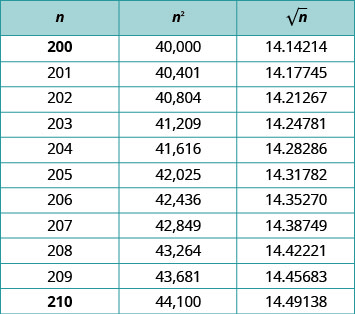
    Ce tableau comporte trois colonnes et onze rangées. Les colonnes sont étiquetées « n », « n au carré » et « racine carrée de n ». Sous la colonne intitulée « n » se trouvent les numéros suivants : 200 ; 201 ; 202 ; 203 ; 204 ; 205 ; 206 ; 207 ; 208 ; 209 ; et 210. Sous la colonne intitulée « n au carré » se trouvent les nombres suivants : 40 000 ; 40 401 ; 40 804 ; 41 209 ; 41 209 ; 41 616 ; 42 025 ; 42 436 ; 42 436 ; 42 849 ; 43 264 ; 43 681 ; 44 100. Sous la colonne intitulée « racine carrée de n » se trouvent les nombres suivants : 14,14214 ; 14,17745 ; 14,21267 ; 14,24781 ; 14,28286 ; 14,31782 ; 14,35270 ; 14,38749 ; 14,42221 ; 14,45683 ; 14,49138.
    Un tableau de racines carrées a été utilisé pour trouver les valeurs approximatives des racines carrées avant l'utilisation de calculateurs.

    Si quelqu'un avait besoin d'approximer une fraction avec une racine carrée dans le dénominateur, cela signifiait faire une division longue avec un diviseur à cinq décimales. Il s'agissait d'un processus très fastidieux.

    C'est pour cette raison qu'un processus appelé rationalisation du dénominateur a été développé. Une fraction dont le dénominateur est un radical est convertie en une fraction équivalente dont le dénominateur est un entier. Ce processus est toujours utilisé aujourd'hui et est également utile dans d'autres domaines des mathématiques.

    Définition : RATIONALISATION DU DÉNOMINATEUR

    Le processus de conversion d'une fraction ayant un radical au dénominateur en une fraction équivalente dont le dénominateur est un entier est appelé rationalisation du dénominateur.

    Les racines carrées des nombres qui ne sont pas des carrés parfaits sont des nombres irrationnels. Lorsque nous rationalisons le dénominateur, nous écrivons une fraction équivalente avec un nombre rationnel dans le dénominateur.

    Regardons un exemple numérique.

    \[\begin{array}{ll} {\text{Suppose we need an approximate value for the fraction.}}&{\frac{1}{\sqrt{2}}}\\ {\text{A five decimal place approximation to} \sqrt{2} \text{is} 1.41421}&{\frac{1}{1.41421}}\\ {\text{Without a calculator, would you want to do this division?}}&{1.41421) \overline{1.0}}\\ \nonumber \end{array}\]

    Mais nous pouvons trouver une fraction équivalente à\(\frac{1}{\sqrt{2}}\) en multipliant le numérateur et le dénominateur par\(\sqrt{2}\).

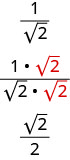
    Cette figure montre trois fractions. La première fraction est égale à 1 au-dessus de la racine carrée de 2. La seconde est 1 fois la racine carrée de 2 sur la racine carrée de 2 fois la racine carrée de 2. La troisième montre la racine carrée de 2 sur 2.

    Maintenant, si nous avons besoin d'une valeur approximative, nous divisons\(2) \overline{1.41421}\). C'est beaucoup plus facile.

    Même si des calculateurs sont disponibles presque partout, une fraction dont le dénominateur comporte un radical doit encore être rationalisée. Il n'est pas considéré comme simplifié si le dénominateur contient une racine carrée.

    De même, une racine carrée n'est pas considérée comme simplifiée si le radical et contient une fraction.

    Définition : RACINES CARRÉES SIMPLIFIÉES

    Une racine carrée est considérée comme simplifiée s'il y a

    • aucun facteur carré parfait dans le radicand
    • aucune fraction dans le radicand
    • aucune racine carrée dans le dénominateur d'une fraction

    Pour rationaliser un dénominateur, nous utilisons la propriété qui\((\sqrt{a})^2=a\). If we square an irrational square root, we get a rational number.

    Nous utiliserons cette propriété pour rationaliser le dénominateur dans l'exemple suivant.

    Exemple\(\PageIndex{19}\)

    Simplifiez :\(\frac{4}{\sqrt{3}}\).

    Réponse

    Pour supprimer la racine carrée du dénominateur, nous la multiplions elle-même. Pour maintenir l'équivalence des fractions, nous multiplions le numérateur et le dénominateur par le même facteur.

      \(\frac{4}{\sqrt{3}}\)

    Multipliez à la fois le numérateur et le dénominateur par\(\sqrt{3}\)    		 \(\frac{4·\sqrt{3}}{\sqrt{3}·\sqrt{3}}\)
    Simplifiez. \(\frac{4\sqrt{3}}{3}\)
    Exemple\(\PageIndex{20}\)

    Simplifiez :\(\frac{5}{\sqrt{3}}\).

    Réponse

    \(\frac{5\sqrt{3}}{3}\)

    Exemple\(\PageIndex{21}\)

    Simplifiez :\(\frac{6}{\sqrt{5}}\).

    Réponse

    \(\frac{6\sqrt{5}}{5}\)

    Exemple\(\PageIndex{22}\)

    Simplifiez :\(−\frac{8}{3\sqrt{6}}\)

    Réponse

    Pour supprimer la racine carrée du dénominateur, nous la multiplions elle-même. Pour maintenir l'équivalence des fractions, nous multiplions le numérateur et le dénominateur par\(\sqrt{6}\).

      .
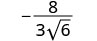
    Multipliez le numérateur et le dénominateur par\(\sqrt{6}\). .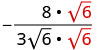
    Simplifiez. .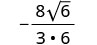
    Supprimez les facteurs courants. .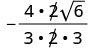
    Simplifiez. .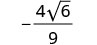
    Exemple\(\PageIndex{23}\)

    Simplifiez :\(\frac{5}{2\sqrt{5}}\).

    Réponse

    \(\frac{\sqrt{5}}{2}\)

    Exemple\(\PageIndex{24}\)

    Simplifiez :\(−\frac{9}{4\sqrt{3}}\).

    Réponse

    \(−\frac{3\sqrt{3}}{4}\)

    Simplifiez toujours d'abord le radical du dénominateur, avant de le rationaliser. De cette façon, les chiffres restent plus petits et plus faciles à utiliser.

    Exemple\(\PageIndex{25}\)

    Simplifiez :\(\sqrt{\frac{5}{12}}\).

    Réponse
      .
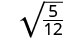
    La fraction n'étant pas un carré parfait, réécrivez-la à l'aide de la propriété
    Quotient.    		 .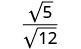
    Simplifiez le dénominateur. .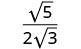
    Rationalisez le dénominateur. .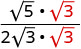
    Simplifiez. .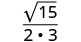
    Simplifiez. .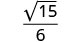
    Exemple\(\PageIndex{26}\)

    Simplifiez :\(\sqrt{\frac{7}{18}}\).

    Réponse

    \(\frac{\sqrt{14}}{6}\)

    Exemple\(\PageIndex{27}\)

    Simplifiez :\(\sqrt{\frac{3}{32}}\).

    Réponse

    \(\frac{\sqrt{6}}{8}\)

    Exemple\(\PageIndex{28}\)

    Simplifiez :\(\sqrt{\frac{11}{28}}\)

    Réponse
      .
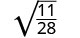
    Réécrivez à l'aide de la propriété Quotient. .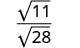
    Simplifiez le dénominateur. .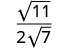
    Rationalisez le dénominateur. .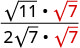
    Simplifiez. .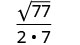
    Simplifiez. .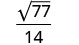
    Exemple\(\PageIndex{29}\)

    Simplifiez :\(\sqrt{\frac{3}{27}}\).

    Réponse

    \(\frac{1}{3}\)

    Exemple\(\PageIndex{30}\)

    Simplifiez :\(\sqrt{\frac{10}{50}}\)

    Réponse

    \(\frac{\sqrt{5}}{5}\)

    Rationaliser un dénominateur à deux termes

    Lorsque le dénominateur d'une fraction est une somme ou une différence avec des racines carrées, nous utilisons le modèle Product of Conjugués pour rationaliser le dénominateur.

    \[\begin{array}{ll} {(a−b)(a+b)}&{(2−\sqrt{5})(2+\sqrt{5})}\\ {a^2−b^2}&{2^2−(\sqrt{5})^2}\\ {}&{4−5}\\ {}&{−1}\\ \nonumber \end{array}\]

    Lorsque nous multiplions un binôme qui inclut une racine carrée par son conjugué, le produit n'a pas de racines carrées.

    Exemple\(\PageIndex{31}\)

    Simplifiez :\(\frac{4}{4+\sqrt{2}}\).

    Réponse
      .
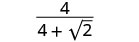
    Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. .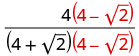
    Multipliez les conjugués dans le dénominateur. .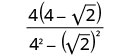
    Simplifiez le dénominateur. .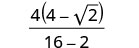
    Simplifiez le dénominateur. .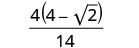
    Supprimez les facteurs communs du numérateur et du dénominateur. .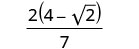
    Nous laissons le numérateur sous forme factorielle afin de faciliter la recherche de facteurs communs après avoir simplifié le dénominateur.  
    Exemple\(\PageIndex{32}\)

    Simplifiez :\(\frac{2}{2+\sqrt{3}}\).

    Réponse

    \(\frac{2(2−\sqrt{3})}{1}\)

    Exemple\(\PageIndex{33}\)

    Simplifiez :\(\frac{5}{5+\sqrt{3}}\).

    Réponse

    \(\frac{5(5−\sqrt{3})}{22}\)

    Exemple\(\PageIndex{34}\)

    Simplifiez :\(\frac{5}{2−\sqrt{3}}\).

    Réponse
      .
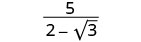
    Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. .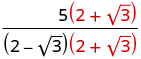
    Multipliez les conjugués dans le dénominateur. .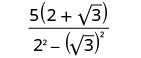
    Simplifiez le dénominateur. .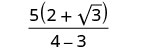
    Simplifiez le dénominateur. .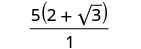
    Simplifiez. .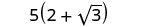
    Exemple\(\PageIndex{35}\)

    Simplifiez :\(\frac{3}{1−\sqrt{5}}\).

    Réponse

    \(−\frac{3(1+\sqrt{5})}{4}\)

    Exemple\(\PageIndex{36}\)

    Simplifiez :\(\frac{2}{4−\sqrt{6}}\).

    Réponse

    \(\frac{4+\sqrt{6}}{5}\)

    Exemple\(\PageIndex{37}\)

    Simplifiez :\(\frac{\sqrt{3}}{\sqrt{u}−\sqrt{6}}\).

    Réponse
      .
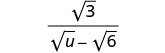
    Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. .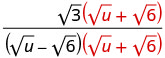
    Multipliez les conjugués dans le dénominateur. .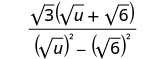
    Simplifiez le dénominateur. .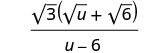
    Exemple\(\PageIndex{38}\)

    Simplifiez :\(\frac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).

    Réponse

    \(\frac{\sqrt{5}(\sqrt{x}−\sqrt{2})}{x−2}\)

    Exemple\(\PageIndex{39}\)

    Simplifiez :\(\frac{\sqrt{10}}{\sqrt{y}−\sqrt{3}}\).

    Réponse

    \(\frac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y−3}\)

    Exemple\(\PageIndex{40}\)

    Simplifiez :\(\frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}−\sqrt{7}}\).

    Réponse
      .
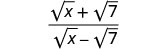
    Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. .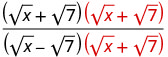
    Multipliez les conjugués dans le dénominateur. .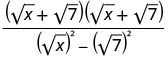
    Simplifiez le dénominateur. .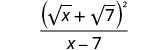
    Nous ne mettons pas le numérateur au carré. Sous forme factorielle, nous pouvons constater qu'il n'y a aucun facteur commun à supprimer du numérateur et du dénominateur.  
    Exemple\(\PageIndex{41}\)

    Simplifiez :\(\frac{\sqrt{p}+\sqrt{2}}{\sqrt{p}−\sqrt{2}}\).

    Réponse

    \(\frac{(\sqrt{p}+\sqrt{2})^2}{p−2}\)

    Exemple\(\PageIndex{42}\)

    Simplifiez :\(\frac{\sqrt{q}−\sqrt{10}}{\sqrt{q}+\sqrt{10}}\).

    Réponse

    \(\frac{(\sqrt{q}−\sqrt{10})^2}{q−10}\)

    Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à diviser et à rationaliser.

    • Diviser et rationaliser

    Concepts clés

    • Propriété du quotient des racines carrées
      • Si a, b sont des nombres réels non négatifs et\(b \ne 0\), alors

        \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)et\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)

    • Racines carrées simplifiées
      Une racine carrée est considérée comme simplifiée s'il y a
      • pas de facteurs carrés parfaits dans le radicand
      • aucune fraction dans le radicand
      • aucune racine carrée dans le dénominateur d'une fraction

    Lexique

    rationaliser le dénominateur
    Le processus de conversion d'une fraction ayant un radical au dénominateur en une fraction équivalente dont le dénominateur est un entier est appelé rationalisation du dénominateur.