Skip to main content
Global

8.9 : Utiliser la variation directe et inverse

  1. Last updated
  2. Save as PDF
  • Page ID
    194796

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Résoudre les problèmes de variation directe
    • Résoudre les problèmes de variation inverse
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    Si vous manquez un problème, revenez à la section répertoriée et passez en revue les informations.

    1. Trouvez l'inverse multiplicatif de −8
      Si vous avez oublié ce problème, passez en revue l'exercice 1.10.13.
    2. Résolvez pour n : 45=20n
      Si vous avez oublié ce problème, passez en revue l'exercice 2.2.1.
    3. Évaluez\(5x^2\) quand x=10
      Si vous avez oublié ce problème, passez en revue l'exercice 1.3.25.

    Lorsque deux quantités sont liées par une proportion, nous disons qu'elles sont proportionnelles l'une à l'autre. Une autre façon d'exprimer cette relation est de parler de la variation des deux quantités. Nous aborderons la variation directe et la variation inverse dans cette section.

    Résoudre les problèmes de variation directe

    Lindsay est payée 15$ de l'heure à son travail. Si nous sommes son salaire et h le nombre d'heures qu'elle a travaillées, nous pourrions modéliser cette situation à l'aide de l'équation

    s = 15 h

    Le salaire de Lindsay est le produit d'une constante, 15, et du nombre d'heures qu'elle travaille. Nous disons que le salaire de Lindsay varie directement en fonction du nombre d'heures qu'elle travaille. Deux variables varient directement si l'une est le produit d'une constante et l'autre.

    Définition : VARIATION DIRECTE

    Pour deux variables x et y quelconques, y varie directement avec x si

    y=kx, où\(n \ne 0\)

    Dans les applications utilisant la variation directe, nous connaîtrons généralement les valeurs d'une paire de variables et nous serons invités à trouver l'équation qui relie x et y. Ensuite, nous pouvons utiliser cette équation pour trouver des valeurs de y pour d'autres valeurs de x.

    Comment résoudre les problèmes de variation directe

    Exemple\(\PageIndex{1}\)

    Si y varie directement avec x et y=20 lorsque x=8, trouvez l'équation qui relie x et y.

    Réponse

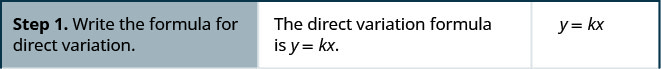
    L'image ci-dessus comporte 3 colonnes. Le tableau indique les étapes à suivre pour résoudre les problèmes de variation directe. La première étape consiste à écrire la formule de la variation directe. La formule de variation directe est y égal à k x. Ensuite, y est égal à k fois x.La deuxième étape consiste à remplacer les valeurs données par les variables. On nous donne y égal 20 et x est égal à 8. Ensuite, nous avons 20 égaux k fois 8.La troisième étape consiste à résoudre la variation constante. Divisez les deux côtés de l'équation par 8, puis multipliez. On obtient maintenant 20 divisé par 8 égal à k. K est égal à 2,5.La quatrième étape consiste à écrire l'équation qui relie x et y. Réécrivez l'équation générale avec la valeur que nous avons trouvée k pour obtenir y égal 2 et cinq dixièmes fois x.

    Exemple\(\PageIndex{2}\)

    Si y varie directement sous la forme x et y=3, lorsque x=10, trouvez l'équation qui relie x et y=3.

    Réponse

    \(y=\frac{3}{10}x\)

    Exemple\(\PageIndex{3}\)

    Si y varie directement comme x et y = 12 lorsque x = 4, trouvez l'équation qui relie x et y.

    Réponse

    y = 3

    Nous allons énumérer les étapes ci-dessous.

    Définition : RÉSOUDRE LES PROBLÈMES DE VARIATION DIRECTE
    1. Écrivez la formule de variation directe.
    2. Remplacez les variables par les valeurs données.
    3. Résolvez la constante de variation.
    4. Écrivez l'équation qui relie x et y.

    Nous allons maintenant résoudre quelques applications de variation directe.

    Exemple\(\PageIndex{4}\)

    Lorsque Raoul court sur le tapis roulant au gymnase, le nombre de calories, c, qu'il brûle varie directement avec le nombre de minutes, m, il utilise le tapis roulant. Il a brûlé 315 calories en utilisant le tapis roulant pendant 18 minutes.

    1. Écrivez l'équation qui relie c et m.
    2. Combien de calories brûlerait-il s'il courait sur le tapis roulant pendant 25 minutes ?
    Réponse

    1.

      Le nombre de calories, c varie directement avec le nombre de minutes, m, sur le tapis roulant, et c = 315 lorsque m = 18
    Écrivez la formule de variation directe. .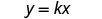
    Nous utiliserons c à la place de y et mm à la place de x. .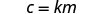
    Remplacez les variables par les valeurs données. .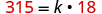
    Résolvez la constante de variation. .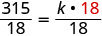
      .
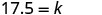
    Écrivez l'équation qui relie c et m. .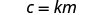
    Remplacez par la constante de variation. .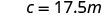

    2.

     

    Trouve c lorsque m=25.
    Écrivez l'équation qui relie c et m. .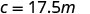
    Remplacez la valeur donnée par m. .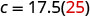
    Simplifiez. .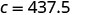
      Raoul brûlerait 437,5 calories s'il utilisait le tapis roulant pendant 25 minutes.
    Exemple\(\PageIndex{5}\)

    Le nombre de calories, c, brûlées varie directement en fonction du temps, t, passé à faire de l'exercice. Arnold a brûlé 312 calories en 65 minutes d'exercice.

    1. Écrivez l'équation qui relie c et t.
    2. Combien de calories brûlerait-il s'il faisait de l'exercice pendant 90 minutes ?
    Réponse
    1. c=4,8 t
    2. 432 calories
    Exemple\(\PageIndex{6}\)

    La distance parcourue par un corps en mouvement, d, varie directement avec le temps, t, il se déplace. Un train parcourt 160 km en 2 heures

    1. Écrivez l'équation qui relie d et t.
    2. Combien de kilomètres parcourrait-il en 5 heures ?
    Réponse
    1. d = 50 t
    2. 250 milles

    Dans l'exemple précédent, les variables c et m étaient nommées dans le problème. Ce n'est généralement pas le cas. Nous devrons nommer les variables dans l'exemple suivant dans le cadre de la solution, comme nous le faisons pour la plupart des problèmes appliqués.

    Exemple\(\PageIndex{7}\)

    Le nombre de gallons d'essence que consomme la voiture d'Eunice varie directement avec le nombre de kilomètres parcourus. La semaine dernière, elle a parcouru 469,8 milles et consommé 14,5 gallons d'essence.

    1. Écrivez l'équation qui relie le nombre de gallons d'essence utilisés au nombre de kilomètres parcourus.
    2. Combien de gallons d'essence consommerait la voiture d'Eunice si elle parcourait 1000 miles ?
    Réponse

    1.

      Le nombre de gallons d'essence varie directement en fonction du nombre de kilomètres parcourus.
    Nous allons d'abord nommer les variables. Soit g = nombre de gallons de gaz.
    m = nombre de miles parcourus.
    Écrivez la formule de variation directe. .
    Nous utiliserons g à la place de y et m à la place de x. .
    Remplacez les variables par les valeurs données .
      .
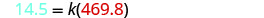
    Résolvez la constante de variation. .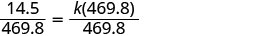
    Nous allons arrondir au millième le plus proche. .
    Écrivez l'équation qui relie g et m. .
    Remplacez par la constante de variation. .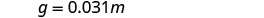

    2.

      Trouve g lorsque m = 1000.
    Écrivez l'équation qui relie g et m. g = 0,031 m
    Remplacez la valeur donnée par m. g=0,031 (1000)
    Simplifiez. g=31
      La voiture d'Eunice consommerait 31 gallons d'essence si elle la parcourait 1 000 miles.

    Notez que dans cet exemple, les unités de la constante de variation sont les gallons/mille. Dans la vie de tous les jours, on parle généralement de miles par gallon.

    Exemple\(\PageIndex{8}\)

    La distance parcourue par Brad varie directement en fonction du temps passé à voyager. Brad a parcouru 660 miles en 12 heures,

    1. Écrivez l'équation qui relie le nombre de miles parcourus au temps.
    2. Combien de kilomètres Brad pourrait-il parcourir en 4 heures ?
    Réponse
    1. m = 55 h
    2. 220 milles
    Exemple\(\PageIndex{9}\)

    Le poids d'un liquide varie directement en fonction de son volume. Un liquide qui pèse 24 livres a un volume de 4 gallons.

    1. Écrivez l'équation qui relie le poids au volume.
    2. Si un liquide a un volume de 13 gallons, quel est son poids ?
    Réponse
    1. p = 6 v
    2. 78 livres

    Dans certains cas, une variable varie directement avec le carré de l'autre variable. Lorsque cela se produit, l'équation de la variation directe est\(y=kx^2\).

    Exemple\(\PageIndex{10}\)

    La charge maximale supportée par une poutre varie directement avec le carré de la diagonale de la section transversale de la poutre. Une poutre d'une diagonale de 4 pouces peut supporter une charge maximale de 75 livres.

    1. Écrivez l'équation qui relie la charge maximale à la section transversale.
    2. Quelle est la charge maximale que peut supporter une poutre d'une diagonale de 8 pouces ?
    Réponse

    1.

      La charge maximale varie directement avec le carré de la diagonale de la section transversale.
    Nommez les variables. Soit L = charge maximale.
    c= la diagonale de la section transversale
    Écrivez la formule de variation directe, où y varie directement avec le carré de x. .
    Nous utiliserons L à la place de y et c à la place de x. .
    Remplacez les variables par les valeurs données. .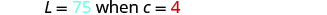
      .
    Résolvez la constante de variation. .
      .
    Écrivez l'équation qui relie L et c. .
    Remplacez par la constante de variation. .

    2.

      Trouve L lorsque c=8.
    Écrivez l'équation qui relie L et c. \(L=4.6875c^2\)
    Remplacez la valeur donnée par c. \(L=4.6875(8)^2\)
    Simplifiez. L=300
      Une poutre d'une diagonale de 8 pouces peut supporter une charge maximale de 300 livres.
    Exemple\(\PageIndex{11}\)

    La distance parcourue par un objet est directement proportionnelle au carré du temps pendant lequel il tombe. Une balle tombe de 144 pieds en 3 secondes.

    1. Écrivez l'équation qui relie la distance au temps.
    2. À quelle distance tombera un objet en 4 secondes ?
    Réponse
    1. \(d=16t^2\)
    2. 256 pieds
    Exemple\(\PageIndex{12}\)

    L'aire d'un cercle varie directement comme le carré du rayon. Une pizza circulaire d'un rayon de 6 pouces a une superficie de 113,04 pouces carrés.

    1. Écrivez l'équation qui relie l'aire au rayon.
    2. Quelle est la surface d'une pizza d'un rayon de 9 pouces ?
    Réponse
    1. \(A=3.14r^2\)
    2. 254,34 pouces carrés

    Résoudre les problèmes de variation inverse

    De nombreuses applications impliquent deux variables qui varient inversement. À mesure qu'une variable augmente, l'autre diminue. L'équation qui les relie est\(y=\frac{k}{x}\).

    Définition : VARIATION INVERSE

    Pour deux variables x et y quelconques, y varie inversement avec x si

    y=\(\frac{k}{x}\), où\(k \ne 0\)

    Le mot « inverse » dans la variation inverse fait référence à l'inverse multiplicatif. L'inverse multiplicatif de x est\(\frac{1}{x}\).

    Nous résolvons les problèmes de variation inverse de la même manière que nous avons résolu les problèmes de variation directe. Seule la forme générale de l'équation a changé. Nous copierons la boîte de procédure ici et remplacerons simplement « direct » par « inverse ».

    Définition : RÉSOUDRE LES PROBLÈMES DE VARIATION INVERSE
    1. Écrivez la formule de la variation inverse.
    2. Remplacez les variables par les valeurs données.
    3. Résolvez la constante de variation.
    4. Écrivez l'équation qui relie x et y.
    Exemple\(\PageIndex{13}\)

    Si y varie inversement avec x et y = 20 lorsque x = 8 x et y.

    Réponse
    Écrivez la formule de la variation inverse. .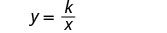
    Remplacez les variables par les valeurs données. .
      .
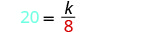
    Résolvez la constante de variation. .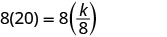
      .
    Écrivez l'équation qui relie x et y. .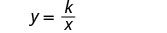
    Remplacez par la constante de variation. .
    Exemple\(\PageIndex{14}\)

    Si p varie inversement avec q et p=30 lorsque q=12, trouvez l'équation qui relie p et q.

    Réponse

    \(p=\frac{360}{q}\)

    Exemple\(\PageIndex{15}\)

    Si y varie inversement avec x et y=8 lorsque x=2, trouvez l'équation qui relie x et y.

    Réponse

    \(y=\frac{16}{x}\)

    Exemple\(\PageIndex{16}\)

    La consommation de carburant (mpg) d'une voiture varie inversement avec son poids. Une voiture qui pèse 3 100 livres atteint 26 mi/gal sur l'autoroute.

    1. Écrivez l'équation de variation.
    2. Quelle serait la consommation de carburant d'une voiture qui pèse 4 030 livres ?
    Réponse

    1.

      La consommation de carburant varie inversement avec le poids.
    Nous allons d'abord nommer les variables. Soit f = consommation de carburant.
    w = poids.
    Écrivez la formule de la variation inverse. .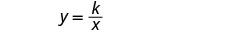
    Nous utiliserons f à la place de y et w à la place de x. .
    Remplacez les variables par les valeurs données. .
      .
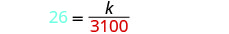
    Résolvez la constante de variation. .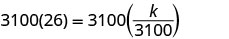
      .
    Écrivez l'équation qui relie f et w. .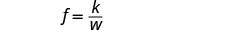
    Remplacez par la constante de variation. .

    2.

      Détermine f lorsque w=4030.
    Écrivez l'équation qui relie f et w. .
    Remplacez la valeur donnée par w. \(f=\frac{80,600}{4030}\)
    Simplifiez. f=20
      Une voiture qui pèse 4 030 livres aurait une consommation de carburant de 20 mi/gal.
    Exemple\(\PageIndex{17}\)

    La valeur d'une voiture varie inversement en fonction de son âge. Elena a acheté une voiture de deux ans pour 20 000$.

    1. Écrivez l'équation de variation.
    2. Quelle sera la valeur de la voiture d'Elena lorsqu'elle aura 5 ans ?
    Réponse
    1. \(v=\frac{40,000}{a}\)
    2. 8 000$
    Exemple\(\PageIndex{18}\)

    Le temps nécessaire pour vider une piscine varie inversement en fonction du débit de pompage. Lucy a mis 2,5 heures à vider sa piscine à l'aide d'une pompe nominale à 400 gal/min (gallons par minute).

    1. Écrivez l'équation de variation.
    2. Combien de temps lui faudra-t-il pour vider la piscine à l'aide d'une pompe nominale à 500 gal/min ?
    Réponse
    1. \(t=\frac{1000}{r}\)
    2. 2 heures
    Exemple\(\PageIndex{19}\)

    La fréquence d'une corde de guitare varie inversement avec sa longueur. Une corde de 26 pouces de long a une fréquence de 440 vibrations par seconde.

    1. Écrivez l'équation de variation.
    2. Combien de vibrations par seconde y aura-t-il si la longueur de la corde est réduite à 20 pouces en plaçant un doigt sur une frette ?
    Réponse

    1.

      La fréquence varie inversement avec la longueur.
    Nommez les variables. Soit f = fréquence.
    L = longueur.
    Écrivez la formule de la variation inverse. .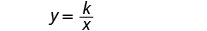
    Nous utiliserons f à la place de y et L à la place de x .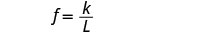
    Remplacez les variables par les valeurs données. .
      .
    Résolvez la constante de variation. .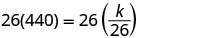
      .
    Écrivez l'équation qui relie f et L. .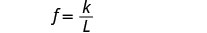
    Remplacez par la constante de variation. .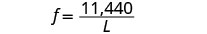

    2.

      Trouve f lorsque L = 20.
    Écrivez l'équation qui relie f et L. \(f=\frac{11,440}{L}\)
    Remplacez la valeur donnée par L. \(f=\frac{11,440}{20}\)
    Simplifiez. f=572
      Une corde de guitare de 20 pouces a une fréquence de 572 vibrations par seconde.
    Exemple\(\PageIndex{20}\)

    Le nombre d'heures nécessaires à la fonte de la glace varie inversement avec la température de l'air. Supposons qu'un bloc de glace fond en 2 heures lorsque la température est de 65 degrés.

    1. Écrivez l'équation de variation.
    2. Combien d'heures faudrait-il pour qu'un même bloc de glace fonde si la température était de 78 degrés ?
    Réponse
    1. \(h=\frac{130}{t}\)
    2. \(1\frac{2}{3}\)heures
    Exemple\(\PageIndex{21}\)

    La force nécessaire pour casser une planche varie inversement en fonction de sa longueur. Richard utilise 24 livres de pression pour casser une planche de 2 pieds de long.

    1. Écrivez l'équation de variation.
    2. Combien de kilos de pression sont nécessaires pour casser une planche de 5 pieds de long ?
    Réponse
    1. \(F=\frac{48}{L}\)
    2. 9,6 livres