8.8 : Résolvez les applications de mouvement et de travail uniformes

Last updated
Save as PDF

Page ID: 194827

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Résolvez des applications de mouvement
Résoudre les applications professionnelles

Avant de commencer, répondez à ce questionnaire de préparation.

Si vous manquez un problème, revenez à la section répertoriée et passez en revue les informations.

Un train express et un bus local partent de Chicago pour se rendre à Champaign. Le bus express peut faire le trajet en 2 heures et le bus local en 5 heures. La vitesse du bus express est de 62 miles par heure plus rapide que la vitesse du bus local. Déterminez la vitesse du bus local.
Si vous avez oublié ce problème, consultez [lien].
Résoudre$\frac{1}{3}x+\frac{1}{4}x=\frac{5}{6}$.
Si vous avez oublié ce problème, consultez [lien].
Résoudre :$18t^2−30=−33t$.
Si vous avez oublié ce problème, consultez [lien].

Résolvez des applications de mouvements

Nous avons résolu des problèmes de mouvement uniforme en utilisant la formule d=RT dans les chapitres précédents. Nous avons utilisé un tableau comme celui ci-dessous pour organiser les informations et nous amener à l'équation.

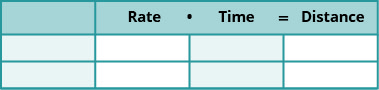
$L'image ci-dessus est un tableau composé de 4 colonnes et de trois rangées. La première ligne est la ligne d'en-tête. La deuxième colonne de la ligne d'en-tête contient le mot « taux ». La troisième colonne contient le mot « Heure ». La quatrième colonne indique « Distance ». Les autres espaces sont vides.$

La formule D=RT suppose que nous connaissons r et t et que nous les utilisons pour trouver D. Si nous connaissons D et r et que nous avons besoin de trouver t, nous résoudrons l'équation de t et obtiendrons la formule$t=\frac{D}{r}$

Nous avons également expliqué comment le fait de voler avec ou contre un courant affecte la vitesse d'un véhicule. Nous reviendrons sur cette idée dans l'exemple suivant.

Exemple$\PageIndex{1}$

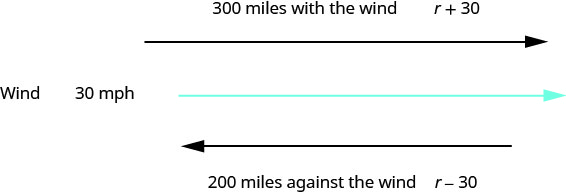
Un avion peut parcourir 200 miles dans un vent de face de 30 mi/h dans le même laps de temps qu'il faut pour parcourir 300 miles avec un vent arrière de 30 mi/h. Quelle est la vitesse de l'avion ?

Solution

Il s'agit d'une situation de mouvement uniforme. Un diagramme nous aidera à visualiser la situation.

$L'image ci-dessus comporte deux flèches parallèles. La pointe de la première flèche pointe vers la droite. Les mots « 300 miles avec le vent », r plus 30 pouces au-dessus de la pointe de la flèche. En dessous se trouve une ligne ondulée. À gauche de la ligne ondulée, il est écrit : « Vent de 30 milles à l'heure ». En dessous se trouve une flèche dont l'extrémité pointe vers la gauche. En dessous se trouvent les mots « 200 milles contre le vent ou moins 30 ».$

Nous remplissons le tableau pour organiser les informations.

Nous cherchons la vitesse de l'avion.	Soit r = la vitesse de l'avion.
Lorsque l'avion vole avec le vent, le vent augmente sa vitesse et la vitesse est de r+30.
Lorsque l'avion vole contre le vent, le vent diminue sa vitesse et la vitesse est de r−30.
Inscrivez les tarifs. Inscrivez les distances. Puisque d=R∙t, nous résolvons pour t et obtenons$\frac{D}{r}$. Nous divisons la distance par le taux de chaque ligne et plaçons l'expression dans la colonne temporelle.	$.$
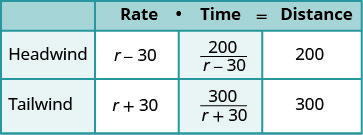Nous savons que les temps sont égaux et nous écrivons donc notre équation.	$\frac{200}{r−30}=\frac{300}{r+30}$
Nous multiplions les deux côtés par l'écran LCD. 200 (r+30) =300 (r−30)
Simplifiez.	(r+30) (200) = (r−30) (300)
	200 r+6000 = 300 r−9 000
Résoudre.	15000 = 100 r 150 = r
Vérifiez.
Est-ce que 150 mi/h est une vitesse raisonnable pour un avion ? Oui. Si l'avion roule à 150 mi/h et que le vent souffle à 30 mi/h :
Vent arrière 150+30 = 180$\frac{300}{180}=\frac{5}{3}$ mi/h
Vent de face 150 à 30 = 120$\frac{200}{120}=\frac{5}{3}$ mi/h
Les temps sont égaux, donc ça vérifie.	L'avion roulait à 150 mi/h.

Essayez-le$\PageIndex{2}$

Link peut faire du vélo sur 20 miles dans un vent de face de 3 mi/h en même temps qu'il peut parcourir 30 miles avec un vent arrière de 3 mi/h. Quelle est la vitesse à vélo de Link ?

Réponse: 15 mi/h

Essayez-le$\PageIndex{3}$

Judy peut naviguer sur son bateau à 5 miles dans un vent de face de 7 mi/h en même temps qu'elle peut parcourir 12 miles avec un vent arrière de 7 mi/h. Quelle est la vitesse du bateau de Judy sans vent ?

Réponse: 17 mi/h

Dans l'exemple suivant, nous connaîtrons le temps total résultant du fait de parcourir différentes distances à différentes vitesses.

Exemple$\PageIndex{4}$

Jazmine s'est entraînée pendant 3 heures samedi. Elle a couru 8 miles puis parcouru 24 miles à vélo. Sa vitesse de vélo est 4 mi/h plus rapide que sa vitesse de course. Quelle est sa vitesse de course ?

Solution

Il s'agit d'une situation de mouvement uniforme. Un diagramme nous aidera à visualiser la situation.

$L'image ci-dessus est une ligne droite avec deux flèches pointant vers la droite. À l'extrême gauche, au-dessus de la ligne, on peut lire « courir » et plus bas, légèrement après la première flèche, on peut lire « vélo ». Légèrement en dessous de la ligne, à l'extrême gauche, avant la première flèche, on peut lire « 8 miles » et à l'extrême droite, après la première flèche, on peut lire « 12 miles ». La région de l'extrême gauche à l'extrême droite de la flèche est groupée pour indiquer que la longueur totale de la ligne est de 3 heures.$

Nous remplissons le tableau pour organiser les informations.

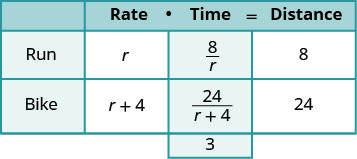
Nous recherchons la vitesse de course de Jazmine.	Soit r = le sp de Jazmine est en cours d'exécution
Sa vitesse à vélo est plus rapide de 4 miles que sa vitesse de course.	r+4 = sa vitesse de vélo
Les distances sont données, saisissez-les dans le graphique.
Puisque d=R∙t, nous résolvons pour t et obtenons$t=\frac{D}{r}$ Nous divisons la distance par le taux dans chaque ligne et plaçons l'expression dans la colonne temporelle.	$.$
Écrivez une phrase verbale.	Son temps et le temps passé à faire du vélo
Traduisez la phrase pour obtenir l'équation.	$\frac{8}{r}+\frac{24}{r+4}=3$
Résoudre.	$r(r+4)(\frac{8}{r}+\frac{24}{r+4})=3r(r+4)$ $8(r+4)+24r=3r^2+12r$ $8r+32+24r=3r^2+12r$ $32+32r=3r^2+12r$ $0=3r^2−20r−32$ $0=(3r+4)(r−8)$
	(3r+4) =0, (r−8) =0
	$r=−\frac{4}{3}$, r=8
Vérifiez. r=8
Une vitesse négative n'a pas de sens dans ce problème, donc r=8 est la solution.
Est-ce que 8 mi/h est une vitesse de course raisonnable ? Oui.
Courez 8 mph,$\frac{8 miles}{8 mph}=1 hour$ Vélo 12 mph,$\frac{24 miles}{12 mph}=2 hours$ 3 heures au total. La vitesse de course de Jazmine est de 8 mph.

Essayez-le$\PageIndex{5}$

Dennis a fait du ski de fond pendant 6 heures samedi. Il a skié 20 milles en montée puis 20 milles en descente, pour revenir à son point de départ. Sa vitesse en montée était inférieure de 5 mi/h à sa vitesse en descente. Quelle était la vitesse de Dennis en montée et sa vitesse en descente ?

Réponse: 10 mi/h

Essayez-le$\PageIndex{6}$

Tony a conduit 4 heures jusqu'à son domicile, parcourant 208 miles sur l'autoroute et 40 miles sur les routes de campagne. S'il roulait 15 mi/h plus vite sur l'autoroute que sur les routes de campagne, quel était son taux sur les routes de campagne ?

Réponse: 50 mi/h

Encore une fois, nous utiliserons la formule de mouvement uniforme résolue pour la variable t.

Exemple$\PageIndex{7}$

Hamilton a descendu à vélo 12 miles sur le sentier fluvial entre sa maison et l'océan, puis a gravi la colline pour rentrer chez lui. Sa vitesse en montée était de 8 milles à l'heure plus lente que sa vitesse en descente. Il lui a fallu 2 heures de plus pour rentrer chez lui que pour rejoindre l'océan. Trouvez la vitesse de descente de Hamilton.

Solution

Il s'agit d'une situation de mouvement uniforme. Un diagramme nous aidera à visualiser la situation.

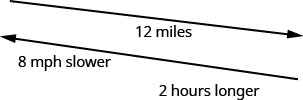
$La figure ci-dessus montre 2 lignes diagonales parallèles pointant dans des directions opposées. La ligne supérieure pointe vers la droite et vers le bas et porte l'inscription « 12 miles » en dessous. La ligne du bas pointe vers la gauche et vers le haut, et est écrit « 8 miles par heure plus lentement, 2 heures de plus » en dessous.$

Nous remplissons le tableau pour organiser les informations.

Nous recherchons la vitesse de descente de Hamilton.	Soit r = la vitesse de descente de Hamilton.
Sa vitesse de montée est plus lente de 8 miles par heure. Entrez les taux dans le graphique.	h−8 = vitesse de montée de Hamilton
La distance est la même dans les deux sens, soit 12 miles. Puisque d=R∙t, nous résolvons pour t et obtenons$t=\frac{D}{r}$ Nous divisons la distance par le taux dans chaque ligne et plaçons l'expression dans la colonne temporelle.	$.$
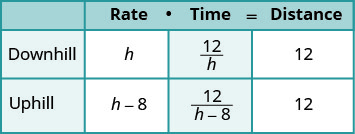Écrivez une phrase verbale sur l'heure.	Il a mis 2 heures de plus en montée qu'en descente. Le temps de montée est 2 de plus que le temps de descente.
Traduisez la phrase pour obtenir l'équation. Résoudre.	$\frac{12}{h−8}=\frac{12}{h}+2$ $h(h−8)(\frac{12}{h−8})=h(h−8)(\frac{12}{h}+2)$ 12 h = 12 (h−8) +2 h (h−8) $12h=12h−96+2h^2−16h$ $0=2h^2−16h−96$ $0=2(h^2−8h−48)$ 0=2 (h−12) (h+4) h−12=0, h+4=0 h=12, h=−4
Vérifiez. Est-ce que 12 km/h sont une vitesse raisonnable pour faire du vélo en descente ? Oui.
Descente 12 mi/h, $\frac{12 miles}{12 mph}=1 hour$
En montée 12−8 = 4 mi/h $\frac{12 miles}{4 mph}=3 hours$
	Le temps de montée est de 2 heures de plus que le temps de descente. La vitesse de descente de Hamilton est de 12 mi/h.

Essayez-le$\PageIndex{8}$

Kayla a fait du vélo à 75 miles pour rentrer de l'université un week-end, puis a pris le bus pour rentrer à l'université. Il lui a fallu 2 heures de moins pour retourner à l'université en bus que pour rentrer chez elle à vélo, et la vitesse moyenne du bus était 10 miles par heure plus rapide que la vitesse de Kayla à vélo. Trouvez la vitesse de vélo de Kayla.

Réponse: 15 mi/h

Essayez-le$\PageIndex{9}$

Victoria fait du jogging sur 20 miles jusqu'au parc le long d'un sentier plat, puis revient en faisant du jogging sur un sentier vallonné de 18 miles. Elle fait du jogging 1 mile à l'heure plus lentement sur le sentier vallonné que sur le sentier plat, et son voyage aller-retour lui prend deux heures de plus. Découvrez son rythme de jogging sur les sentiers plats.

Réponse: 6 mi/h

Résoudre les applications professionnelles

Supposons que Pete puisse peindre une pièce en 10 heures. S'il travaille à un rythme soutenu, il peindra$\frac{1}{10}$ la pièce en 1 heure. Si Alicia prenait 8 heures pour peindre la même pièce, alors en 1 heure elle peindrait$\frac{1}{8}$ la pièce. Combien de temps faudrait-il à Pete et Alicia pour peindre la pièce s'ils travaillaient ensemble (et n'interféraient pas avec la progression de chacun) ?

Il s'agit d'une application « professionnelle » typique. Trois facteurs entrent en jeu : le temps qu'il faudrait à chacune des deux personnes pour faire le travail seule et le temps qu'il leur faudrait pour faire le travail ensemble.

Revenons à Pete et Alicia qui peignent la pièce. Nous indiquerons le nombre d'heures qu'il leur faudrait pour peindre la pièce ensemble. Ainsi, en 1 heure de travail ensemble, ils ont terminé$\frac{1}{t}$ le travail.

En une heure, Pete a fait$\frac{1}{10}$ son travail. Alicia a fait$\frac{1}{8}$ le travail. Et ensemble, ils ont fait$\frac{1}{t}$ leur travail.

Nous pouvons modéliser cela avec le mot équation, puis le traduire en une équation rationnelle. Pour trouver le temps qu'il leur faudrait s'ils travaillaient ensemble, nous résolvons le problème.

	$.$
	$.$
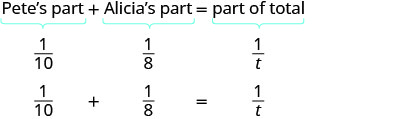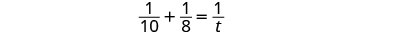Multipliez par l'écran LCD, 40t	$.$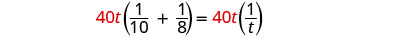
Distribuez.	$.$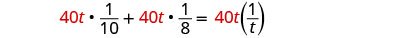
Simplifiez et résolvez.	$.$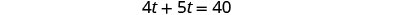
	$.$
	$.$
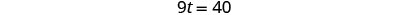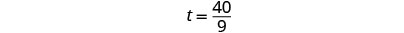Nous allons écrire sous forme de nombre mixte afin de pouvoir le convertir en heures et en minutes.	$.$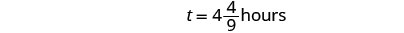
N'oubliez pas que 1 heure = 60 minutes.	$.$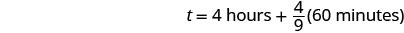
Multipliez, puis arrondissez à la minute la plus proche.	$.$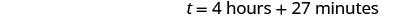
	Pete et Alica mettraient environ 4 heures et 27 minutes pour peindre la pièce.

N'oubliez pas qu'il faut moins de temps à deux personnes pour terminer un travail en travaillant ensemble qu'à l'une ou l'autre personne pour le faire seule.

Exemple$\PageIndex{10}$

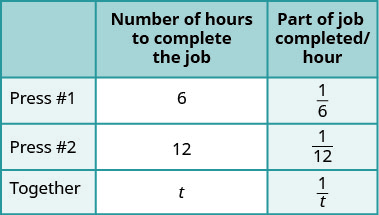
Le magazine hebdomadaire à potins raconte une grande histoire sur le bébé de la princesse et l'éditeur souhaite que le magazine soit imprimé le plus rapidement possible. Elle a demandé à l'imprimeur de faire fonctionner une presse supplémentaire pour accélérer l'impression. Appuyez sur #1 pour faire le travail et appuyez sur #2 prend 12 heures pour faire le travail. Combien de temps faudra-t-il à l'imprimante pour imprimer le magazine avec les deux presses fonctionnant simultanément ?

Solution

C'est un problème de travail. Un tableau nous aidera à organiser l'information.

Soit t le nombre d'heures nécessaires pour effectuer le travail ensemble.
Entrez les heures par travail pour Appuyez sur #1, Appuyez sur #2 et quand ils travaillent ensemble. Si une tâche sur Press #1 prend 6 heures, elle est terminée au bout$\frac{1}{6}$ d'une heure. De même, trouvez la partie du travail terminée/les heures pour Appuyez sur #2 et quand ils travaillent tous les deux ensemble.	$.$
Écrivez une phrase verbale.
La partie terminée en appuyant sur #1 plus la partie terminée en appuyant sur #2 est égale à la quantité terminée ensemble.
Traduisez en une équation.	$.$
Résoudre.	$.$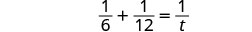
Multipliez par l'écran LCD, 12t.	$.$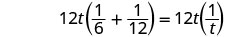
Simplifiez.	$.$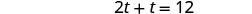
	$.$
	$.$
	Lorsque les deux presses fonctionnent, il faut 4 heures pour faire le travail.

Essayez-le$\PageIndex{11}$

Un jardinier peut tondre un terrain de golf en 4 heures, tandis qu'un autre peut tondre le même terrain de golf en 6 heures. Combien de temps faudrait-il aux deux jardiniers pour tondre le terrain de golf ?

Réponse: 2 heures et 24 minutes

Essayez-le$\PageIndex{12}$

Carrie peut désherber le jardin en 7 heures, tandis que sa mère peut le faire en 3 heures. Combien de temps leur faudra-t-il pour travailler ensemble ?

Réponse: 2 heures et 6 minutes

Exemple$\PageIndex{13}$

Corey peut déblayer toute la neige du trottoir et de l'allée en 4 heures. Si lui et son jumeau Casey travaillent ensemble, ils peuvent finir de pelleter la neige en 2 heures. Combien d'heures faudrait-il à Casey pour faire le travail tout seul ?

Solution

Il s'agit d'une application professionnelle. Un tableau nous aidera à organiser l'information.
Nous cherchons le nombre d'heures qu'il faudrait à Casey pour terminer le travail tout seul.
Soit t le nombre d'heures nécessaires à Casey pour terminer.
Entrez le nombre d'heures par travail pour Corey, Casey et le temps qu'ils travaillent ensemble. Si Corey prend 4 heures, le travail est terminé en 1 heure$\frac{1}{4}$. De même, trouvez la partie du travail accomplie/les heures pour Casey et le moment où ils travaillent tous les deux ensemble.	$.$
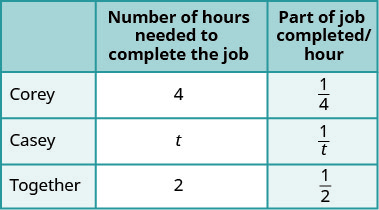Écrivez une phrase verbale.
La partie complétée par Corey plus la partie complétée par Casey est égale au montant complété ensemble.
Traduisez en une équation :	$.$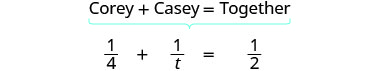
Résoudre.	$.$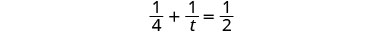
Multipliez par l'écran LCD, 4t.	$.$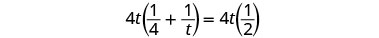
Simplifiez.	$.$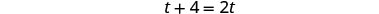
	$.$
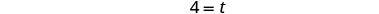	Il faudrait 4 heures à Casey pour faire le travail seul.

Essayez-le$\PageIndex{14}$

Deux tuyaux peuvent remplir une piscine en 10 heures. Il faudrait 26 heures à un tuyau pour remplir la piscine tout seul. Combien de temps faudrait-il à l'autre tuyau, travaillant seul, pour remplir la piscine ?

Réponse: 16,25 heures

Essayez-le$\PageIndex{15}$

Cara et Cindy, travaillant ensemble, peuvent ratisser la cour en 4 heures. Travaillant seule, Cindy met 6 heures à ratisser la cour. Combien de temps faudrait-il à Cara pour ratisser la cour seule ?

Réponse: 12 heures

La pratique rend parfait

Résolvez des applications de mouvements

Dans les exercices suivants, résolvez des applications de mouvement uniforme

Essayez-le$\PageIndex{16}$

Mary fait une visite guidée à bord d'un hélicoptère capable de parcourir 450 miles contre un vent de face de 35 mi/h en même temps qu'elle peut parcourir 702 miles avec un vent arrière de 35 mi/h. Détermine la vitesse de l'hélicoptère.

Solution

160 mi/h

Exercice$\PageIndex{17}$

Un jet privé peut parcourir 1 210 miles contre un vent de face de 25 mi/h en même temps qu'il peut parcourir 1 694 miles avec un vent arrière de 25 mi/h. Trouve la vitesse du jet.

Essayez-le$\PageIndex{18}$

Un bateau parcourt 140 miles en aval en même temps qu'il parcourt 92 miles en amont. La vitesse du courant est de 10 km/h. Quelle est la vitesse du bateau ?

Réponse: 29 mi/h

Exercice$\PageIndex{19}$

Darrin peut faire du skateboard de 2 miles contre un vent de 4 mph en même temps qu'il fait du skateboard 10 miles avec un vent de 4 mph. Trouvez les planches à roulettes Speed Darrin sans vent.

Essayez-le$\PageIndex{20}$

Jane a passé 2 heures à explorer une montagne avec un vélo tout-terrain. Lorsqu'elle a parcouru les 40 milles de montée, elle a roulé 5 mi/h plus lentement que lorsqu'elle a atteint le sommet et a parcouru 12 milles le long du sommet. Quel était son taux le long du sommet ?

Réponse: 30 mi/h

Exercice$\PageIndex{21}$

Jill voulait perdre du poids alors elle a prévu une journée d'exercice. Elle a passé au total 2 heures à faire du vélo et à faire du jogging. Elle a parcouru 12 miles à vélo et fait du jogging sur 6 miles. Son rythme pour le jogging était inférieur de 10 mi/h à celui du vélo. Quel était son rythme lorsqu'elle faisait du jogging ?

Essayez-le$\PageIndex{22}$

Bill voulait essayer différentes embarcations. Il a parcouru 62 milles en aval à bord d'un bateau à moteur et 27 milles en aval à bord d'un jet ski. Sa vitesse sur le jet ski était 10 mi/h plus rapide que sur le bateau à moteur. Bill a passé un total de 4 heures sur l'eau. Quel était son taux de vitesse sur le bateau à moteur ?

Réponse: 20 mi/h

Exercice$\PageIndex{23}$

Nancy a fait 3 heures de route. Elle a parcouru 80 km avant d'être prise dans une tempête. Elle a ensuite parcouru 68 milles à 9 mi/h de moins que lorsqu'il faisait beau. Quelle était sa vitesse pendant la tempête ?

Essayez-le$\PageIndex{24}$

Chester a fait une montée de 24 miles à vélo, puis est redescendu à 2 mi/h plus vite que sa montée. S'il lui a fallu 2 heures de plus pour monter que pour descendre, quel était son rythme de montée ?

Réponse: 4 mi/h

Exercice$\PageIndex{25}$

Matthew a fait du jogging jusqu'à la maison de son ami à 20 miles de là, puis a été raccompagné chez lui. Il lui a fallu 2 heures de plus pour y faire du jogging que pour le retour. Sa vitesse de jogging était inférieure de 25 mi/h à celle qu'il faisait lorsqu'il roulait. Quel était son rythme de jogging ?

Essayez-le$\PageIndex{26}$

Hudson parcourt 1080 miles en jet, puis 240 miles en voiture pour se rendre à une réunion d'affaires. Le jet roule 300 mi/h plus vite que la voiture, et le trajet en voiture dure 1 heure de plus que le jet. Quelle est la vitesse de la voiture ?

Réponse: 60 mi/h

Exercice$\PageIndex{27}$

Nathan a marché sur un sentier asphalté pendant 12 miles. Il a parcouru les 12 miles qui l'ont conduit à sa voiture sur une route de gravier à travers la forêt. Sur l'asphalte, il marchait 2 milles à l'heure plus vite que sur le gravier. La marche sur le gravier a duré une heure de plus que la marche sur l'asphalte. À quelle vitesse a-t-il marché sur le gravier ?

Essayez-le$\PageIndex{28}$

John peut piloter son avion à 2800 miles avec une vitesse de vent de 50 mi/h tout en parcourant 2400 miles contre le vent. Si la vitesse du vent est de 50 mi/h, trouvez la vitesse de son avion.

Réponse: 650 mi/h

Exercice$\PageIndex{29}$

Le hors-bord de Jim peut parcourir 20 miles en amont contre un courant de 3 mi/h en même temps qu'il parcourt 22 miles en aval avec une vitesse actuelle de 3 mi/h. Trouve la vitesse du bateau de Jim.

Essayez-le$\PageIndex{30}$

Hazel doit se rendre chez sa petite-fille en avion et en louant une voiture. Elle parcourt 900 miles en avion et 250 miles en voiture. L'avion se déplace 250 mi/h plus vite que la voiture. Si elle conduit la voiture de location pendant 2 heures de plus que dans l'avion, trouvez la vitesse de la voiture.

Réponse: 50 mi/h

Exercice$\PageIndex{31}$

Stu s'est entraîné pendant 3 heures hier. Il a couru 14 miles puis parcouru 40 miles à vélo. Sa vitesse de vélo est 6 mi/h plus rapide que sa vitesse de course. Quelle est sa vitesse de course ?

Essayez-le$\PageIndex{32}$

Pendant le trajet de 9 heures pour rentrer chez elle, Sharon a parcouru 390 miles sur l'autoroute et 240 miles sur les routes de campagne. Sa vitesse sur l'autoroute était 15 de plus que sur les routes de campagne. Quelle était sa vitesse sur les routes de campagne ?

Réponse: 50 mi/h

Exercice$\PageIndex{33}$

Deux sœurs aiment s'affronter lors de leurs balades à vélo. Tamara peut aller 4 km/h plus vite que sa sœur, Samantha. S'il faut 1 heure de plus à Samantha qu'à Tamara pour parcourir 130 miles, à quelle vitesse Samantha peut-elle faire du vélo ?

Résoudre les applications professionnelles

Dans les exercices suivants, résolvez des applications professionnelles.

Essayez-le$\PageIndex{34}$

Mike, maçon expérimenté, peut construire un mur en 3 heures, tandis que son fils, qui apprend, peut faire le travail en 6 heures. Combien de temps leur faut-il pour construire un mur ensemble ?

Réponse: 2 heures

Exercice$\PageIndex{35}$

Sam met 4 heures à ratisser la pelouse avant tandis que son frère, Dave, peut ratisser la pelouse en 2 heures. Combien de temps leur faudra-t-il pour ratisser la pelouse en travaillant ensemble ?

Essayez-le$\PageIndex{36}$

Mary peut nettoyer son appartement en 6 heures tandis que sa colocataire peut nettoyer l'appartement en 5 heures. S'ils travaillent ensemble, combien de temps leur faudrait-il pour nettoyer l'appartement ?

Réponse: 2 heures et 44 minutes

Exercice$\PageIndex{37}$

Brian peut poser une dalle de béton en 6 heures, tandis que Greg peut le faire en 4 heures. Si Brian et Greg travaillent ensemble, combien de temps cela prendra-t-il ?

Essayez-le$\PageIndex{38}$

Leeson peut relire une copie de journal en 4 heures. Si Ryan les aide, ils peuvent faire le travail en 3 heures. Combien de temps faudrait-il à Ryan pour faire son travail seul ?

Réponse: 12 heures

Exercice$\PageIndex{39}$

Paul peut nettoyer le sol d'une classe en 3 heures. Lorsque son assistant l'aide, le travail dure 2 heures. Combien de temps faudrait-il à l'assistant pour le faire seul ?

Essayez-le$\PageIndex{40}$

Joséphine peut corriger les épreuves de ses élèves en 5 heures, mais si l'assistante de son professeur l'aide, cela leur prendra 3 heures. Combien de temps faudrait-il à l'assistant pour le faire seul ?

Réponse: 7 heures et 30 minutes

Exercice$\PageIndex{41}$

Laver seul la voiture de son père, Levi, huit ans, prend deux heures et demie. Si son père l'aide, cela prend 1 heure. Combien de temps faut-il au père de Levi's pour laver la voiture tout seul ?

Essayez-le$\PageIndex{42}$

Jackson peut enlever les bardeaux d'une maison en 7 heures, tandis que Martin peut enlever les bardeaux en 5 heures. Combien de temps leur faudra-t-il pour enlever le zona s'ils travaillent ensemble ?

Réponse: 2 heures et 55 minutes

Exercice$\PageIndex{43}$

À la fin de la journée, Dodie peut nettoyer son salon de coiffure en 15 minutes. Ann, qui travaille avec elle, peut nettoyer le salon en 30 minutes. Combien de temps leur faudrait-il pour nettoyer l'atelier s'ils travaillaient ensemble ?

Essayez-le$\PageIndex{44}$

Ronald peut déblayer l'allée en 4 heures, mais si son frère Donald l'aide, cela prendra 2 heures. Combien de temps faudrait-il à Donald pour déblayer l'allée tout seul ?

Réponse: 4 heures

Exercice$\PageIndex{45}$

Tina met 3 heures à congeler ses biscuits des Fêtes, mais si Candy l'aide, cela prend 2 heures. Combien de temps faudrait-il à Candy pour congeler elle-même les biscuits des Fêtes ?

Mathématiques quotidiennes

Essayez-le$\PageIndex{46}$

Dana aime promener son chien, mais parfois son chien s'enfuit et elle doit courir après lui. Dana a promené son chien sur 11 miles, mais a ensuite dû courir sur 1 mile, passant un total de 2,5 heures avec son chien. Sa vitesse de course était de 3 mi/h plus rapide que sa vitesse de marche. Trouve sa vitesse de marche.

Réponse: 3 mi/h

Exercice$\PageIndex{47}$

Ken et Joe quittent leur appartement pour aller voir un match de football à 72 km. Ken conduit sa voiture 30 mph plus vite que Joe peut faire du vélo. S'il faut 2 heures de plus à Joe que Ken pour accéder au jeu, quelle est la vitesse de Joe ?

Exercices d'écriture

Exercice$\PageIndex{48}$

Dans l'exemple, la solution h=-4 est barrée. Expliquez pourquoi.

Exercice$\PageIndex{49}$

Paula et Yuki sont colocataires. Paula met 3 heures pour nettoyer leur appartement. Yuki met 4 heures pour nettoyer l'appartement. L'équation$\frac{1}{3}+\frac{1}{4}=\frac{1}{t}$ peut être utilisée pour trouver t, le nombre d'heures qu'il leur faudrait à tous les deux, travaillant ensemble, pour nettoyer leur appartement. Expliquez comment cette équation modélise la situation.

Auto-vérification

ⓐ Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

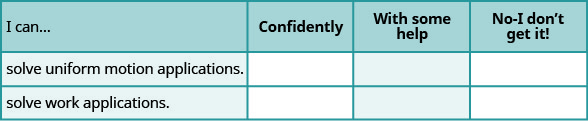
$Ce tableau comporte trois lignes et quatre colonnes. La première ligne est une ligne d'en-tête et elle étiquette chaque colonne. La première colonne est intitulée « Je peux... », la deuxième « En toute confiance », la troisième « Avec de l'aide » et la dernière « Non, je ne comprends pas ». Dans la colonne « Je peux... », la ligne suivante indique « Résoudre des applications à mouvement uniforme ». La rangée suivante se lit comme suit : « Résoudre les demandes de travail ». Les colonnes restantes sont vides.$

ⓑ Sur une échelle de 1 à 10, comment évalueriez-vous votre maîtrise de cette section à la lumière de vos réponses à la liste de contrôle ? Comment pouvez-vous améliorer cela ?