8.2 : Multiplier et diviser des expressions rationnelles
- Page ID
- 194922
À la fin de cette section, vous serez en mesure de :
- Multipliez les expressions
- Divisez les expressions
Avant de commencer, répondez à ce questionnaire de préparation.
Si vous manquez un problème, revenez à la section répertoriée et passez en revue les informations.
- Multipliez :\(\frac{14}{15}·\frac{6}{35}\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.6.13. - Diviser :\(\frac{14}{15}÷\frac{6}{35}\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.6.22. - Facteur complètement :\(2x^2−98\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.5.10. - Facteur complètement :\(10n^3+10\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.5.19. - Facteur complètement :\(10p^2−25pq−15q^2\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.5.28.
Multipliez les expressions
Pour multiplier les expressions rationnelles, nous faisons exactement ce que nous avons fait avec des fractions numériques. Nous multiplions les numérateurs et multiplions les dénominateurs. Ensuite, s'il existe des facteurs communs, nous les supprimons pour simplifier le résultat.
Si p, q, r, s sont des polynômes où\(q \ne 0\) et\(s \ne 0\)
\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)Pour multiplier les expressions rationnelles, multipliez les numérateurs et multipliez les dénominateurs.
Nous allons faire le premier exemple avec des fractions numériques pour nous rappeler comment nous avons multiplié des fractions sans variables.
Multipliez :\(\frac{10}{28}·\frac{8}{15}\).
- Réponse
-
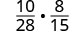
Multipliez les numérateurs et les dénominateurs. 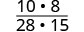
Recherchez les facteurs communs, puis supprimez-les. 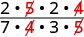
Simplifiez. 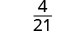
Multipliez :\(\frac{6}{10}·\frac{15}{12}\).
- Réponse
-
\(\frac{3}{4}\)
Multipliez :\(\frac{20}{15}·\frac{6}{8}\).
- Réponse
-
1
N'oubliez pas que tout au long de ce chapitre, nous supposerons que toutes les valeurs numériques qui donneraient au dénominateur zéro sont exclues. Nous n'écrirons pas les restrictions pour chaque expression rationnelle, mais gardez à l'esprit que le dénominateur ne peut jamais être zéro. Donc, dans l'exemple suivant,\(x \ne 0\) and \(y \ne 0\).
Multipliez :\(\frac{2x}{3y^2}·\frac{6xy^3}{x^{2}y}\).
- Réponse
-
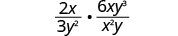
Multipliez. 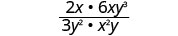
Factoriez complètement le numérateur et le dénominateur, puis supprimez les facteurs communs. 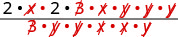
Simplifiez. 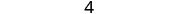
Multipliez :\(\frac{3pq}{q^2}·\frac{5p^{2}q}{6pq}\).
- Réponse
-
\(\frac{5p^2}{2q}\)
Multipliez :\(\frac{6x^{3}y}{7x^2}·\frac{2xy}{3x^{2}y}\).
- Réponse
-
\(\frac{12y^3}{7}\)
Comment multiplier les expressions rationnelles
Multipliez :\(\frac{2x}{x^2-7x+12}·\frac{x^2−9}{6x^2}\).
- Réponse
-
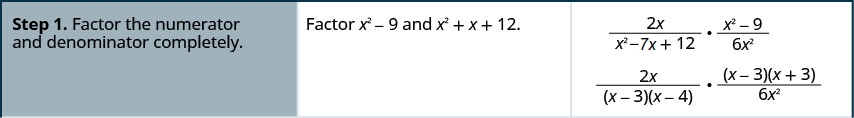


Multipliez :\(\frac{5x}{x^2+5x+6}·\frac{x^2−4}{10x}\).
- Réponse
-
\(\frac{x−2}{2(x+3)}\)
Multipliez :\(\frac{9x^2}{x^2+11x+30}·\frac{x^2−36}{3x^2}\).
- Réponse
-
\(\frac{3(x−6)}{x+5}\)
- Facturez complètement chaque numérateur et dénominateur.
- Multipliez les numérateurs et les dénominateurs.
- Simplifiez en divisant les facteurs communs.
Multipliez :\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\).
- Réponse
-
\(\frac{n^2−7n}{n^2+2n+1}·\frac{n+1}{2n}\) Facturez chaque numérateur et dénominateur. \(\frac{n(n−7)}{(n+1)(n+1)}·\frac{n+1}{2n}\) Multipliez les numérateurs et les dénominateurs. \(\frac{n(n−7)(n+1)}{(n+1)(n+1)2n}\) Simplifiez. \(\frac{n−7}{2(n+1)}\)
Multipliez :\(\frac{x^2−25}{x^2−3x−10}·\frac{x+2}{x}\).
- Réponse
-
\(\frac{x+5}{x}\)
Multipliez :\(\frac{x^2−4x}{x^2+5x+6}·\frac{x+2}{x}\).
- Réponse
-
\(\frac{x−4}{x+3}\)
Multipliez :\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\).
- Réponse
-
\(\frac{16−4x}{2x−12}·\frac{x^2−5x−6}{x^2−16}\) Facturez chaque numérateur et dénominateur. \(\frac{4(4−x)}{2(x−6)}·\frac{(x−6)(x+1)}{(x−4)(x+4)}\) Multipliez les numérateurs et les dénominateurs. \(\frac{4(4−x)(x−6)(x+1)}{2(x−6)(x−4)(x+4)}\) Simplifiez. \(−\frac{2(x+1)}{(x+4)}\)
Multipliez :\(\frac{12x−6x^2}{x^2+8x}·\frac{x^2+11x+24}{x^2−4}\).
- Réponse
-
\(−\frac{6(x+3)}{x+2}\)
Multipliez :\(\frac{9v−3v^2}{9v+36}·\frac{v^2+7v+12}{v^2−9}\).
- Réponse
-
\(−\frac{v}{3}\)
Multipliez :\(\frac{2x−6}{x^2−8x+15}·\frac{x^2−25}{2x+10}\).
- Réponse
-
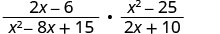
Facturez chaque numérateur et dénominateur. 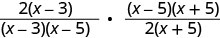
Multipliez les numérateurs et les dénominateurs. 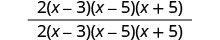
Supprimez les facteurs courants. 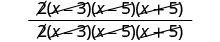
Simplifiez. 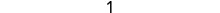
Multipliez :\(\frac{3a−21}{a^2−9a+14}·\frac{a^2−4}{3a+6}\).
- Réponse
-
1
Multipliez :\(\frac{b^2−b}{b^2+9b−10}·\frac{b^2−100}{b^2−10b}\).
- Réponse
-
1
Divisez les expressions
Pour diviser les expressions rationnelles, nous multiplions la première fraction par l'inverse de la seconde, comme nous l'avons fait pour les fractions numériques.
Souvenez-vous, la réciproque\(\frac{a}{b}\) de nous\(\frac{b}{a}\). Pour trouver l'inverse, il suffit de placer le numérateur dans le dénominateur et le dénominateur dans le numérateur. Nous « inversons » la fraction.
Si p, q, r, s sont des polynômes où\(q \ne 0\),\(r \ne 0\),\( s \ne 0\)
\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
Pour diviser des expressions rationnelles, multipliez la première fraction par l'inverse de la seconde.
Comment diviser les expressions rationnelles
Diviser :\(\frac{x+9}{6−x}÷\frac{x^2−81}{x−6}\).
- Réponse
-




Diviser :\(\frac{c+3}{5−c}÷\frac{c^2−9}{c−5}\).
- Réponse
-
\(−\frac{1}{c−3}\)
Diviser :\(\frac{2−d}{d−4}÷\frac{4−d^2}{4−d}\).
- Réponse
-
\(−\frac{1}{2+d}\)
- Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde.
- Facturez complètement les numérateurs et les dénominateurs.
- Multipliez les numérateurs et les dénominateurs ensemble.
- Simplifiez en divisant les facteurs communs.
Diviser :\(\frac{3n^2}{n^2−4n}÷\frac{9n^2−45n}{n^2−7n+10}\).
- Réponse
-
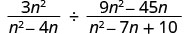
Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde. 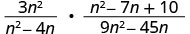
Factoriez les numérateurs et les dénominateurs, puis multipliez. 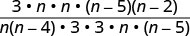
Simplifiez en divisant les facteurs communs. 
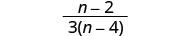
Diviser :\(\frac{2m^2}{m^2−8m}÷\frac{8m^2+24m}{m^2+m−6}\).
- Réponse
-
\(\frac{(m−2)}{4(m−8)}\)
Diviser :\(\frac{15n^2}{3n^2+33n}÷\frac{5n−5}{n^2+9n−22}\).
- Réponse
-
\(\frac{n(n−2)}{n−1}\)
N'oubliez pas de réécrire d'abord la division en multipliant la première expression par l'inverse de la seconde. Ensuite, considérez tout et recherchez les facteurs communs.
Diviser :\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\).
- Réponse
-
\(\frac{2x^2+5x−12}{x^2−16}÷\frac{2x^2−13x+15}{x^2−8x+16}\) Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde. \(\frac{2x^2+5x−12}{x^2−16}·\frac{x^2−8x+16}{2x^2−13x+15}\) Factoriez les numérateurs et les dénominateurs, puis multipliez. \(\frac{(2x−3)(x+4)(x−4)(x−4)}{(x−4)(x+4)(2x−3)(x−5)}\) Simplifiez. \(\frac{(x−4)}{(x−5)}\)
Diviser :\(\frac{3a^2−8a−3}{a^2−25}÷\frac{3a^2−14a−5}{a^2+10a+25}\).
- Réponse
-
\(\frac{(a−3)(a+5)}{(a−5)(a−5)}\)
Diviser :\(\frac{4b^2+7b−2}{1−b^2}÷\frac{4b^2+15b−4}{b^2−2b+1}\).
- Réponse
-
\(−\frac{(b+2)(b−1)}{(1+b)(b+4)}\)
Diviser :\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\).
- Réponse
-
\(\frac{p^3+q^3}{2p^2+2pq+2q^2}÷\frac{p^2−q^2}{6}\) Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde. \(\frac{p^3+q^3}{2p^2+2pq+2q^2}·\frac{6}{p^2−q^2}\) Factoriez les numérateurs et les dénominateurs, puis multipliez. \(\frac{(p+q)(p^2−pq+q^2)6}{2(p^2+pq+q^2)(p−q)(p+q)}\) Simplifiez. \(\frac{3(p^2−pq+q^2)}{(p−q)(p^2+pq+q^2)}\)
Diviser :\(\frac{x^3−8}{3x^2−6x+12}÷\frac{x^2−4}{6}\).
- Réponse
-
\(\frac{2(x^2+2x+4)}{(x+2)(x^2−2x+4)}\)
Diviser :\(\frac{2z^2}{z^2−1}÷\frac{z^3−z^2+z}{z^3−1}\).
- Réponse
-
\(\frac{2z(z^2+z+1)}{(z+1)(z^2−z+1)}\)
Avant de passer à l'exemple suivant, voyons comment diviser une fraction par un nombre entier. Quand on divise\(\frac{3}{5}÷4\)
\[\begin{array}{c} {\frac{3}{5}÷4}\\ {\frac{3}{5}÷\frac{4}{1}}\\ {\frac{3}{5}·\frac{1}{4}}\\ \nonumber \end{array}\]
Nous faisons de même lorsque nous divisons des expressions rationnelles.
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\).
- Réponse
-
\(\frac{a^2−b^2}{3ab}÷(a^2+2ab+b^2)\) Écrivez la deuxième expression sous forme de fraction. \(\frac{a^2−b^2}{3ab}÷\frac{a^2+2ab+b^2}{1}\) Réécrivez la division comme si la première expression était multipliée par l'inverse de la seconde expression. \(\frac{a^2−b^2}{3ab}·\frac{1}{a^2+2ab+b^2}\) Factoriez les numérateurs et les dénominateurs, puis multipliez. \(\frac{(a−b)(a+b)1}{3ab·(a+b)(a+b)}\) Simplifiez. \(\frac{a−b}{3ab(a+b)}\)
\(\frac{2x^2−14x−16}{4}÷(x2+2x+1)\).
- Réponse
-
\(\frac{x−8}{2(x+1)}\)
\(\frac{y^2−6y+8}{y^2−4y}÷(3y2−12y)\).
- Réponse
-
\(\frac{y−2}{3y(y−4)}\)
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\).
- Réponse
-
\(\frac{\frac{6x^2−7x+2}{4x−8}}{\frac{2x^2−7x+3}{x^2−5x+6}}\) Réécrivez avec un signe de division. \(\frac{6x^2−7x+2}{4x−8}÷\frac{2x^2−7x+3}{x^2−5x+6}\) Réécrivez comme le produit de la première fois l'inverse de la seconde. \(\frac{6x^2−7x+2}{4x−8}·\frac{x^2−5x+6}{2x^2−7x+3}\) Factoriez les numérateurs et les dénominateurs, puis multipliez \(\frac{(2x−1)(3x−2)(x−2)(x−3)}{4(x−2)(2x−1)(x−3)}\) Simplifiez. \(\frac{3x−2}{4}\)
\(\frac{\frac{3x^2+7x+2}{4x+24}}{\frac{3x^2−14x−5}{x^2+x−30}}\).
- Réponse
-
\(\frac{x+2}{4}\)
\(\frac{\frac{y^2−36}{2y^2+11y−6}}{\frac{2y^2−2y−60}{8y−4}}\).
- Réponse
-
\(\frac{2}{y+5}\)
Si nous avons plus de deux expressions rationnelles avec lesquelles travailler, nous suivons toujours la même procédure. La première étape sera de réécrire toute division sous forme de multiplication par l'inverse. Ensuite, nous factorisons et multiplions.
\(\frac{3x−6}{4x−4}·\frac{x^2+2x−3}{x^2−3x−10}÷\frac{2x+12}{8x+16}\).
- Réponse
-
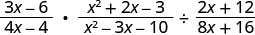
Réécrivez la division sous forme de multiplication par l'inverse. 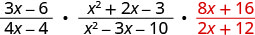
Factoriez les numérateurs et les dénominateurs, puis multipliez. 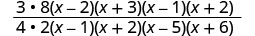
Simplifiez en divisant les facteurs communs. 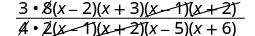
Simplifiez. 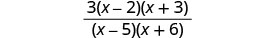
\(\frac{4m+4}{3m−15}·\frac{m^2−3m−10}{m^2−4m−32}÷\frac{12m−36}{6m−48}\).
- Réponse
-
\(\frac{2(m+1)(m+2)}{3(m+4)(m−3)}\)
\(\frac{2n^2+10n}{n−1}÷\frac{n^2+10n+24}{n^2+8n−9}·\frac{n+4}{8n^2+12n}\).
- Réponse
-
\(\frac{(n+5)(n+9)}{2(n+6)(2n+3)}\)
Concepts clés
- Multiplication des expressions rationnelles
- Si p, q, r, s sont des polynômes où\(q \ne 0\) et\(s \ne 0\), alors\(\frac{p}{q}·\frac{r}{s}=\frac{pr}{qs}\)
- Pour multiplier les expressions rationnelles, multipliez les numérateurs et multipliez les dénominateurs
- Multipliez une expression rationnelle
- Facturez complètement chaque numérateur et dénominateur.
- Multipliez les numérateurs et les dénominateurs.
- Simplifiez en divisant les facteurs communs.
- Division des expressions rationnelles
- Si p, q, r, s sont des polynômes où\(q \ne 0\),\(r \ne 0\),\( s \ne 0\), alors\(\frac{p}{q}÷\frac{r}{s}=\frac{p}{q}·\frac{s}{r}\)
- Pour diviser des expressions rationnelles, multipliez la première fraction par l'inverse de la seconde.
- Divisez les expressions
- Réécrivez la division comme le produit de la première expression rationnelle et de l'inverse de la seconde.
- Facturez complètement les numérateurs et les dénominateurs.
- Multipliez les numérateurs et les dénominateurs ensemble.
- Simplifiez en divisant les facteurs communs.


