7.6E : Exercices
- Page ID
- 194619
La pratique rend la perfection
Utiliser la propriété Zero Product
Dans les exercices suivants, résolvez.
\((x−3)(x+7)=0\)
- Réponse
-
\(x=3\), l'ensemble de solutions est\(x=−7\) donc le suivant :\(\{3, -7\}\)
\((y−11)(y+1)=0\)
\((3a−10)(2a−7)=0\)
- Réponse
-
\(a=\frac{10}{3}\), l'ensemble de solutions est\(a=\frac{7}{2}\) donc le suivant :\(\Big\{\tfrac{10}{3}, \tfrac{7}{2}\Big\}\)
\((5b+1)(6b+1)=0\)
\(6m(12m−5)=0\)
- Réponse
-
\(m=0\), l'ensemble de solutions est\(m=\frac{5}{12}\) donc le suivant :\(\Big\{0, \tfrac{5}{12}\Big\}\)
\(2x(6x−3)=0\)
\((y−3)^2=0\)
- Réponse
-
\(y=3\)l'ensemble de solutions est donc :\(\{3\}\)
\((b+10)^2=0\)
\((2x−1)^2=0\)
- Réponse
-
\(x=\frac{1}{2}\)l'ensemble de solutions est donc :\(\Big\{\tfrac{1}{2}\Big\}\)
\((3y+5)^2=0\)
Résoudre des équations quadratiques par factorisation
Dans les exercices suivants, résolvez.
\(x^2+7x+12=0\)
- Réponse
-
\(x=−3\), l'ensemble de solutions est\(x=−4\) donc le suivant :\(\{-3, -4\}\)
\(y^2−8y+15=0\)
\(5a^2−26a=24\)
- Réponse
-
\(a=−\tfrac{4}{5}\), l'ensemble de solutions est\(a=6\) donc le suivant :\(\Big\{−\tfrac{4}{5}, 6\Big\}\)
\(4b^2+7b=−3\)
\(4m^2=17m−15\)
- Réponse
-
\(m=\frac{5}{4}\), l'ensemble de solutions est\(m=3\) donc le suivant :\(\Big\{\tfrac{5}{4}, 3\Big\}\)
\(n^2=5−6n\)
\(7a^2+14a=7a\)
- Réponse
-
\(a=−1\), l'ensemble de solutions est\(a=0\) donc le suivant :\(\{-1, 0\}\)
\(12b^2−15b=−9b\)
\(49m^2=144\)
- Réponse
-
\(m=\frac{12}{7}\), l'ensemble de solutions est\(m=−\frac{12}{7}\) donc le suivant :\(\Big\{−\tfrac{12}{7}, \tfrac{12}{7}\Big\}\)
\(625=x^2\)
\((y−3)(y+2)=4y\)
- Réponse
-
\(y=−1\), l'ensemble de solutions est\(y=6\) donc le suivant :\(\{-1, 6\}\)
\((p−5)(p+3)=−7\)
\((2x+1)(x−3)=−4x\)
- Réponse
-
\(x=\frac{3}{2}\), l'ensemble de solutions est\(x=−1\) donc le suivant :\(\Big\{-1,\tfrac{3}{2}\Big\}\)
\((x+6)(x−3)=−8\)
\(16p^3=24p^2−9p\)
- Réponse
-
\(p=0\), l'ensemble de solutions est\(p=\frac{3}{4}\) donc le suivant :\(\Big\{0,\tfrac{3}{4}\Big\}\)
\(m^3−2m^2=−m\)
\(20x^2−60x=−45\)
- Réponse
-
\(x=\frac{3}{2}\)l'ensemble de solutions est donc :\(\Big\{\tfrac{3}{2}\Big\}\)
\(3y^2−18y=−27\)
Résolvez des applications modélisées par des équations quadratiques
Dans les exercices suivants, résolvez.
Le produit de deux nombres entiers consécutifs est 56. Trouve les nombres entiers.
- Réponse
-
7 et 8 ; −8 et −7
Le produit de deux entiers consécutifs est 42. Trouve les nombres entiers.
La superficie d'un tapis rectangulaire est de 28 pieds carrés. La longueur est supérieure de trois pieds à la largeur. Déterminez la longueur et la largeur du tapis.
- Réponse
-
4 pieds et 7 pieds
Un mur de soutènement rectangulaire a une superficie de 15 pieds carrés. La hauteur du mur est inférieure de deux pieds à sa longueur. Détermine la hauteur et la longueur du mur.
Un fanion a la forme d'un triangle droit, avec une hypoténuse de 10 pieds. La longueur d'un côté du fanion est plus longue de deux pieds que celle de l'autre côté. Détermine la longueur des deux côtés du fanion.
- Réponse
-
6 pieds et 8 pieds
Un bassin réfléchissant a la forme d'un triangle droit, avec un pied le long du mur d'un bâtiment. L'hypoténuse mesure 9 pieds de plus que le côté le long du bâtiment. Le troisième côté mesure 7 pieds de plus que le côté le long du bâtiment. Déterminez la longueur des trois côtés du bassin réfléchissant.
Pratique mixte
Dans les exercices suivants, résolvez.
(x+8) (x−3) =0
- Réponse
-
\(x=−8, \; x=3\)l'ensemble de solutions est donc :\(\{-8, 3\}\)
(3y−5) (y+7) =0
\(p^2+12p+11=0\)
- Réponse
-
\(p=−1, \;p=−11\)l'ensemble de solutions est donc :\(\{-11, -1\}\)
\(q^2−12q−13=0\)
\(m^2=6m+16\)
- Réponse
-
\(m=−2, \; m=8\)l'ensemble de solutions est donc :\(\{-2, 8\}\)
\(4n^2+19n=5\)
\(a^3−a^2−42a=0\)
- Réponse
-
\(a=0, \;a=−6, \;a=7\)l'ensemble de solutions est donc :\(\{-6, 0, 7\}\)
\(4b^2−60b+224=0\)
Le produit de deux nombres entiers consécutifs est 110. Trouve les nombres entiers.
- Réponse
-
10 et 11 ; −11 et −10
La longueur d'une jambe d'un triangle droit est supérieure de trois à celle de l'autre jambe. Si l'hypoténuse est de 15, déterminez la longueur des deux jambes.
Mathématiques quotidiennes
Surface d'un patio Si chaque côté d'un patio carré est augmenté de 4 pieds, la superficie du patio serait de 196 pieds carrés. Résolvez l'équation (s+4) 2=196 (s+4) 2=196 pour s afin de déterminer la longueur d'un côté du patio.
- Réponse
-
10 pieds
Goutte de pastèque Une pastèque est larguée du dixième étage d'un bâtiment. Résolvez l'équation −16t2+144=0−16t2+144=0 pour tt afin de déterminer le nombre de secondes nécessaires à la pastèque pour atteindre le sol.
Exercices d'écriture
Expliquez comment résoudre une équation quadratique. Combien de réponses espérez-vous obtenir pour une équation quadratique ?
- Réponse
-
Les réponses peuvent varier pour l'explication. Vous ne devez pas vous attendre à plus de 2 solutions pour une équation quadratique. Il a souvent deux solutions, mais parfois, il peut y avoir une solution répétée ou même aucune solution.
Donnez un exemple d'équation quadratique qui a un GCF et dont aucune des solutions n'est nulle.
Auto-vérification
a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.
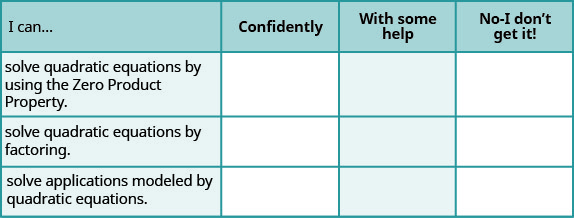
b. Dans l'ensemble, après avoir examiné la liste de contrôle, pensez-vous être bien préparé pour la section suivante ? Pourquoi ou pourquoi pas ?


