7.6 : Équations quadratiques
- Page ID
- 194606
À la fin de cette section, vous serez en mesure de :
- Résolvez des équations quadratiques en utilisant la propriété Zero Product
- Résoudre des équations quadratiques : factorisation
- Résolvez des applications modélisées par des équations quadratiques
Avant de commencer, répondez à ce questionnaire de préparation.
- Résoudre :\(5y−3=0\).
Si vous avez oublié ce problème, passez en revue l'exercice 2.3.1. - Résoudre :\(10a=0\).
Si vous avez oublié ce problème, passez en revue l'exercice 2.2.1. - Combinez des termes similaires :\(12 x^{2}-6 x+4 x\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.3.37. - Facteur\(n^{3}-9 n^{2}-22 n\) complètement.
Si vous avez oublié ce problème, passez en revue l'exercice 7.3.10.
Nous avons déjà résolu des équations linéaires, des équations de forme\(a x+b y=c\). Dans les équations linéaires, les variables n'ont aucun exposant. Les équations quadratiques sont des équations dans lesquelles la variable est au carré. Voici quelques exemples d'équations quadratiques :
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
La variable ne semble pas être au carré dans la dernière équation, mais lorsque nous simplifierons l'expression de gauche, nous obtiendrons\(n^{2}+n\).
La forme générale d'une équation quadratique est\(a x^{2}+b x+c=0\), avec\(a \neq 0\).
Une équation de la forme\(a x^{2}+b x+c=0\) est appelée équation quadratique.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
Pour résoudre des équations quadratiques, nous avons besoin de méthodes différentes de celles que nous avons utilisées pour résoudre des équations linéaires. Nous examinerons une méthode ici, puis plusieurs autres dans un chapitre ultérieur.
Résoudre des équations quadratiques en utilisant la propriété de produit zéro
Nous allons d'abord résoudre certaines équations quadratiques en utilisant la propriété Zero Product. La propriété Zero Product indique que si le produit de deux quantités est nul, au moins l'une des quantités doit être nulle. La seule façon d'obtenir un produit égal à zéro est de le multiplier par zéro lui-même.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
Nous allons maintenant utiliser la propriété Zero Product pour résoudre une équation quadratique.
Résoudre :\((x+1)(x-4)=0\)
- Réponse
-



Résoudre :\((x-3)(x+5)=0\)
- Réponse
-
\(x=3, x=-5\)
Résoudre :\((y-6)(y+9)=0\)
- Réponse
-
\(y=6, y=-9\)
Nous allons généralement travailler un peu plus que dans ce dernier exemple pour résoudre les équations linéaires résultant de l'utilisation de la propriété Zero Product.
Résoudre :\((5 n-2)(6 n-1)=0\)
- Réponse
-
\((5 n-2)(6 n-1)=0\) Utilisez la propriété Zero Product pour définir
chaque facteur sur 0.\(5 n-2=0 \)
\(6 n-1=0\) Résolvez les équations. \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) Vérifiez vos réponses. 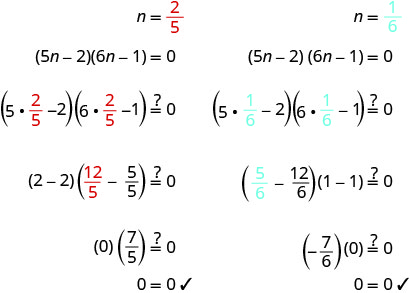
Résoudre :\((3 m-2)(2 m+1)=0\)
- Réponse
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
Résoudre :\((4 p+3)(4 p-3)=0\)
- Réponse
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
Remarquez que lorsque nous avons vérifié les solutions, chacune d'elles a créé un seul facteur égal à zéro. Mais le produit était nul pour les deux solutions.
Résoudre :\(3 p(10 p+7)=0\)
- Réponse
-
\(3p(10p+7)=0\) Utilisez la propriété Zero Product pour définir
chaque facteur sur 0.3 p = 0 10 p+7 = 0 Résolvez les équations. p=0 10 p = −7 \(p=-\frac{7}{10}\) Vérifiez vos réponses. 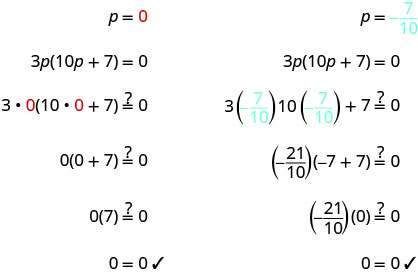
Résoudre :\(2 u(5 u-1)=0\)
- Réponse
-
\(u=0, u=\frac{1}{5}\)
Résoudre :\(w(2 w+3)=0\)
- Réponse
-
\(w=0, w=-\frac{3}{2}\)
Il peut sembler qu'il n'y ait qu'un seul facteur dans l'exemple suivant. N'oubliez pas, cependant, que\((y-8)^{2}\) cela signifie\((y-8)(y-8)\).
Résoudre :\((y-8)^{2}=0\)
- Réponse
-
\((y−8)^{2}=0\) Réécrivez le côté gauche en tant que produit. (y−8) (y−8) =0 Utilisez la propriété Zero Product et
définissez chaque facteur sur 0.y−8=0 y−8=0 Résolvez les équations. y=8 y=8 Lorsqu'une solution se répète, nous l'appelons
racine double.Vérifiez votre réponse. 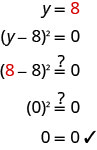
Résoudre :\((x+1)^{2}=0\)
- Réponse
-
\(x=1\)
Résoudre :\((v-2)^{2}=0\)
- Réponse
-
\(v=2\)
Résoudre des équations quadratiques par factorisation
Chacune des équations que nous avons résolues dans cette section jusqu'à présent avait un côté sous forme factorielle. Pour utiliser la propriété Zero Product, l'équation quadratique doit être factorisée, avec zéro sur un côté. Nous sommes donc sûrs de commencer par l'équation quadratique sous forme standard,\(a x^{2}+b x+c=0\). Ensuite, nous prenons en compte l'expression de gauche.
Résoudre :\(x^{2}+2 x-8=0\)
- Réponse
-

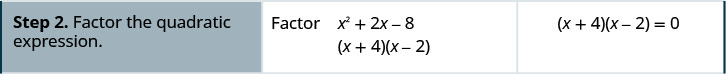



Résoudre :\(x^{2}-x-12=0\)
- Réponse
-
\(x=4, x=-3\)
Résoudre :\(b^{2}+9 b+14=0\)
- Réponse
-
\(b=-2, b=-7\)
- Écrivez l'équation quadratique sous forme standard,\(a x^{2}+b x+c=0\).
- Facturez l'expression quadratique.
- Utilisez la propriété Zero Product.
- Résolvez les équations linéaires.
- Vérifiez.
Avant de procéder à la factorisation, nous devons nous assurer que l'équation quadratique est sous forme standard.
Résoudre :\(2 y^{2}=13 y+45\)
- Réponse
-
\(2 y^{2}=13 y+45\) Écrivez l'équation quadratique sous forme standard. \(2 y^{2}-13 y-45=0\) Facturez l'expression quadratique. \((2 y+5)(y-9)=0\) Utilisez la propriété Zero Product
pour définir chaque facteur sur 0.\(2 y+5=0\) \(y-9=0\) Résolvez chaque équation. \(y=-\frac{5}{2}\) \(y=9\) Vérifiez vos réponses. 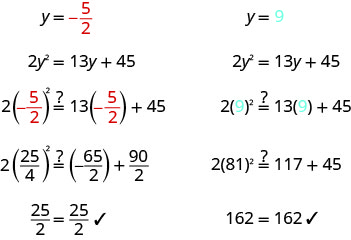
Résoudre :\(3 c^{2}=10 c-8\)
- Réponse
-
\(c=0, c=\frac{4}{3}\)
Résoudre :\(2 d^{2}-5 d=3\)
- Réponse
-
\(d=3, d=-\frac{1}{2}\)
Résoudre :\(5 x^{2}-13 x=7 x\)
- Réponse
-
\(5 x^{2}-13 x=7 x\) Écrivez l'équation quadratique sous forme standard. \(5 x^{2}-20 x=0\) Facturez le côté gauche de l'équation. \(5 x(x-4)=0\) Utilisez la propriété Zero Product
pour définir chaque facteur sur 0.\(5x=0\) \(x−4=0\) Résolvez chaque équation. \(x=0\) \(x=4\) Vérifiez vos réponses. 
Résoudre :\(6 a^{2}+9 a=3 a\)
- Réponse
-
\(a=0, a=-1\)
Résoudre :\(45 b^{2}-2 b=-17 b\)
- Réponse
-
\(b=0, b=-\frac{1}{3}\)
Pour résoudre des équations quadratiques par factorisation, vous utiliserez toutes les techniques de factorisation que vous avez apprises dans ce chapitre ! Reconnaissez-vous le modèle spécial du produit dans l'exemple suivant ?
Résoudre :\(144 q^{2}=25\)
- Réponse
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
Résoudre :\(25 p^{2}=49\)
- Réponse
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
Résoudre :\(36 x^{2}=121\)
- Réponse
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
Dans l'exemple suivant, le côté gauche est pris en compte, mais le côté droit n'est pas zéro. Pour utiliser la propriété Zero Product, un côté de l'équation doit être zéro. Nous allons multiplier les facteurs, puis écrire l'équation sous forme standard.
Résoudre :\((3 x-8)(x-1)=3 x\)
- Réponse
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
Résoudre :\((2 m+1)(m+3)=12 m\)
- Réponse
-
\(m=1, m=\frac{3}{2}\)
Résoudre :\((k+1)(k-1)=8\)
- Réponse
-
\(k=3, k=-3\)
La propriété Zéro produit s'applique également au produit de trois facteurs ou plus. Si le produit est égal à zéro, au moins l'un des facteurs doit être nul. Nous pouvons résoudre certaines équations de degrés supérieurs à deux en utilisant la propriété Zero Product, tout comme nous avons résolu des équations quadratiques.
Résoudre :\(9 m^{3}+100 m=60 m^{2}\)
- Réponse
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Résoudre :\(8 x^{3}=24 x^{2}-18 x\)
- Réponse
-
\(x=0, x=\frac{3}{2}\)
Résoudre :\(16 y^{2}=32 y^{3}+2 y\)
- Réponse
-
\(y=0, y=\frac{1}{4}\)
Lorsque nous factorisons l'équation quadratique dans l'exemple suivant, nous obtenons trois facteurs. Cependant, le premier facteur est une constante. Nous savons que ce facteur ne peut pas être égal à 0.
Résoudre :\(4 x^{2}=16 x+84\)
- Réponse
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Résoudre :\(18 a^{2}-30=-33 a\)
- Réponse
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
Résoudre :\(123 b=-6-60 b^{2}\)
- Réponse
-
\(b=2, b=\frac{1}{20}\)
Résolvez des applications modélisées par des équations quadratiques
La stratégie de résolution de problèmes que nous avons utilisée précédemment pour les applications qui se traduisent en équations linéaires fonctionnera tout aussi bien pour les applications qui se traduisent en équations quadratiques. Nous allons copier la stratégie de résolution des problèmes ici afin de pouvoir l'utiliser à titre de référence.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
- Traduisez en une équation. Il peut être utile de reformuler le problème en une phrase avec toutes les informations importantes. Traduisez ensuite la phrase anglaise en une équation d'algèbre.
- Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
Nous allons commencer par un problème numérique pour nous entraîner à traduire des mots en une équation quadratique.
Le produit de deux entiers consécutifs est\(132 .\) Find the Integers.
- Réponse
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
Le produit de deux entiers consécutifs est\(240 .\) Find the Integers.
- Réponse
-
\(-15,-16\)et\(15,16\)
Le produit de deux entiers consécutifs est\(420 .\) Find the Integers.
- Réponse
-
\(-21,-20\)et\(20,21\)
Avez-vous été surpris par la paire d'entiers négatifs qui constitue l'une des solutions à l'exemple précédent ? Le produit des deux nombres entiers positifs et le produit des deux nombres entiers négatifs donnent tous deux 132.
Dans certaines applications, des solutions négatives résulteront de l'algèbre, mais ne seront pas réalistes compte tenu de la situation.
Un jardin rectangulaire a une superficie de 15 pieds carrés. La longueur du jardin est supérieure de deux pieds à la largeur. Déterminez la longueur et la largeur du jardin.
- Réponse
-
Étape 1 Lisez le problème. En cas de problèmes impliquant des figures géométriques, un croquis peut vous aider à visualiser la situation. 
Étape 2 Identifiez ce que vous recherchez. Nous recherchons la longueur et la largeur. Étape 3 Nommez ce que vous recherchez.
La longueur est supérieure de deux pieds à la largeur.Soit W = la largeur du jardin.
W + 2 = la longueur du jardinÉtape 4. Traduisez en une équation.
Réaffirmez les informations importantes dans une phrase.
La superficie du jardin rectangulaire est de 15 pieds carrés.Utilisez la formule pour l'aire d'un rectangle. \(A=L \cdot W\) Substituez les variables. \(15=(W+2) W\) Étape 5. Résolvez l'équation. Distribuez d'abord. \(15=W^{2}+2 W\) Mets zéro sur un côté. \(0=W^{2}+2 W-15\) Tenez compte du trinôme. \(0=(W+5)(W-3)\) Utilisez la propriété Zero Product. \(0=W+5\) \(0=W−3\) Résolvez chaque équation. \(−5=W\) \(3=W\) Puisque W est la largeur du jardin,
cela n'a aucun sens qu'il soit
négatif. Nous éliminons cette valeur pour W.\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
La largeur est de 3 pieds.Détermine la valeur de la longueur. \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) La longueur est de 5 pieds. Étape 6. Vérifiez la réponse.
La réponse a-t-elle du sens ?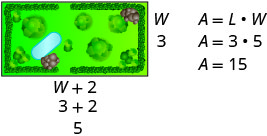
Oui, c'est logique. Étape 7. Réponds à la question. La largeur du jardin est de 3 pieds
et la longueur de 5 pieds.
Un panneau rectangulaire a une superficie de 30 pieds carrés. La longueur du panneau est supérieure d'un pied à la largeur. Déterminez la longueur et la largeur du panneau.
- Réponse
-
55 pieds et 66 pieds
Un patio rectangulaire a une superficie de 180 pieds carrés. La largeur du patio est inférieure de trois pieds à la longueur. Trouvez la longueur et la largeur du patio.
- Réponse
-
12 pieds et 15 pieds
Dans un chapitre précédent, nous avons utilisé le théorème de Pythagore\(\left(a^{2}+b^{2}=c^{2}\right)\). Il a donné la relation entre les jambes et l'hypoténuse d'un triangle droit.
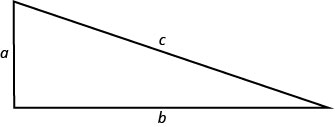
Nous utiliserons cette formule dans l'exemple suivant.
Justine souhaite aménager une terrasse dans le coin de son jardin en forme de triangle droit, comme indiqué ci-dessous. L'hypoténuse mesurera 17 pieds de long. La longueur d'un côté sera inférieure de 7 pieds à la longueur de l'autre côté. Déterminez la longueur des côtés du pont.
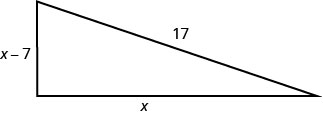
- Réponse
-
Étape 1 Lisez le problème. Étape 2 Identifiez ce que vous recherchez. Nous cherchons la longueur des côtés
du tablier.Étape 3 Nommez ce que vous recherchez.
Un côté est 7 de moins que l'autre.Soit x = longueur d'un côté du pont
x − 7 = longueur de l'autre côtéÉtape 4. Traduisez en une équation.
Comme il s'agit d'un triangle droit, nous pouvons utiliser le théorème de
Pythagore.\(a^{2}+b^{2}=c^{2}\) Substituez les variables. \(x^{2}+(x-7)^{2}=17^{2}\) Étape 5. Résolvez l'équation. \(x^{2}+x^{2}-14 x+49=289\) Simplifiez. \(2 x^{2}-14 x+49=289\) C'est une équation quadratique, alors mettez zéro sur un côté. \(2 x^{2}-14 x-240=0\) Facteur : le plus grand facteur commun. \(2\left(x^{2}-7 x-120\right)=0\) Tenez compte du trinôme. \(2(x-15)(x+8)=0\) Utilisez la propriété Zero Product. \(2\neq 0\) \(x−15=0\) \(x+8=0\) Résoudre. \(2\neq 0\) \(x=15\) \(x=-8\) Puisque\(x\) c'est un côté du triangle,\(x=−8\) cela n'a aucun
sens.\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) Trouve la longueur de l'autre côté. Si la longueur d'un côté est \(x=15\) alors la longueur de l'autre côté est \(x-7\) \(15 - 7 = 8\) 8 est la longueur de l'autre côté. Étape 6. Vérifiez la réponse.
Ces chiffres ont-ils du sens ?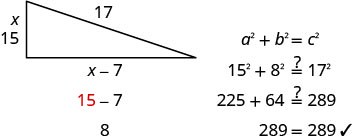
Étape 7. Réponds à la question. Les côtés du pont mesurent 8, 15 et 17 pieds.
La voile d'un bateau est un triangle droit. La longueur d'un côté de la voile est supérieure de 7 pieds à celle de l'autre côté. L'hypoténuse est de 13. Déterminez la longueur des deux côtés de la voile.
- Réponse
-
5 pieds et 12 pieds
Un jardin de méditation a la forme d'un triangle droit, avec une jambe de 7 pieds. La longueur de l'hypoténuse est supérieure d'un à la longueur de l'une des autres jambes. Déterminez la longueur de l'hypoténuse et de l'autre jambe.
- Réponse
-
24 pieds et 25 pieds
Concepts clés
- Propriété de produit nulle Si\(a \cdot b=0\), alors a=0 ou b=0 ou les deux. Voir l'exemple.
- Résoudre une équation quadratique par factorisation Pour résoudre une équation quadratique par factorisation : voir Exemple.
- Écrivez l'équation quadratique sous forme standard,\(a x^{2}+b x+c=0\).
- Facturez l'expression quadratique.
- Utilisez la propriété Zero Product.
- Résolvez les équations linéaires.
- Vérifiez.
- Utilisez une stratégie de résolution de problèmes pour résoudre les problèmes de mots Voir l'exemple.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
- Traduisez en une équation. Il peut être utile de reformuler le problème en une phrase avec toutes les informations importantes. Traduisez ensuite la phrase anglaise en une équation d'algèbre.
- Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
Lexique
- équations quadratiques
- sont des équations dans lesquelles la variable est au carré.
- Propriété de produit nulle
- La propriété Zero Product indique que, si le produit de deux quantités est nul, au moins l'une des quantités est nulle.


