7.5 : Stratégie générale de factorisation des polynômes
- Page ID
- 194631
À la fin de cette section, vous serez en mesure de :
- Reconnaître et utiliser la méthode appropriée pour factoriser complètement un polynôme
Avant de commencer, répondez à ce questionnaire de préparation.
- Facteur\(y^{2}-2 y-24\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.2.19. - Facteur\(3 t^{2}+17 t+10\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.3.28. - Facteur\(36 p^{2}-60 p+25\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.4.1. - Facteur\(5 x^{2}-80\).
Si vous avez oublié ce problème, passez en revue l'exercice 7.4.31.
Reconnaître et utiliser la méthode appropriée pour factoriser complètement un polynôme
Vous avez maintenant pris connaissance de toutes les méthodes d'affacturage dont vous aurez besoin dans ce cours. (Dans votre prochain cours d'algèbre, d'autres méthodes seront ajoutées à votre répertoire.) La figure ci-dessous résume toutes les méthodes d'affacturage que nous avons abordées. La figure\(\PageIndex{1}\) décrit une stratégie que vous devez utiliser lors de la factorisation de polynômes.

- Y a-t-il un plus grand facteur commun ?
- Tenez-le en compte.
- Le polynôme est-il binomial, trinomial ou existe-t-il plus de trois termes ?
- S'il s'agit d'un binôme :
est-ce une somme ?- Des carrés ? Les sommes des carrés ne sont pas prises en compte.
- Des cubes ? Utilisez le modèle de somme des cubes.
- Des carrés ? Facteur comme produit des conjugués.
- Des cubes ? Utilisez la différence de motif de cubes.
- S'il s'agit d'un trinôme :
est-ce de la forme\(x^{2}+b x+c ?\) ? Annuler FOIL.
Est-ce de la forme\(a x^{2}+b x+c\) ?- Si aa et cc sont des carrés, vérifiez s'ils correspondent au motif carré trinomial.
- Utilisez la méthode des essais et des erreurs ou « ac ».
- S'il contient plus de trois termes :
utilisez la méthode de regroupement.
- S'il s'agit d'un binôme :
- Vérifiez.
- Est-ce complètement pris en compte ?
- Les facteurs se multiplient-ils jusqu'au polynôme d'origine ?
N'oubliez pas qu'un polynôme est complètement factorisé si, à l'exception des monômes, ses facteurs sont premiers !
Facteur complet :\(4 x^{5}+12 x^{4}\)
- Réponse
-
\ (\ begin {array} {lll} \ text {Y a-t-il un GCF ? } & \ text {Oui,} 4 x^ {4} & 4 x^ {5} +12 x^ {4} \ \ \ text {Facturez le GCF.} & &4 x^ {4} (x+3) \ \ \ text {Entre parenthèses, est-ce un binôme, un} & & \ \ \ text {trinomial, ou existe-t-il plus de trois termes ? } & \ text {Binomial.} & \ \ \ quad \ text {Est-ce une somme ? } & & \ text {Oui.} \ \ \ quad \ text {De carrés ? Des cubes ? } & & \ text {Non.} \ \ \ text {Vérification.}
\ \ \ \ \ \ quad \ text {L'expression est-elle complètement prise en compte ? } & & \ text {Oui.} \ \ \ quad \ text {Multipliez.} \ \ \ begin {array} {l} {4 x^ {4} (x+3)} \ \ {4 x^ {4} \ cdot x+4 x^ {4} \ cdot 3} \ \ {4 x^ {5} +12 x^ {4}} \ coche \ end {tableau} \ {end tableau} \)
Facteur complet :\(3 a^{4}+18 a^{3}\)
- Réponse
-
3\(a^{3}(a+6)\)
Facteur complet :\(45 b^{6}+27 b^{5}\)
- Réponse
-
9\(b^{5}(5 b+3)\)
Facteur complet :\(12 x^{2}-11 x+2\)
- Réponse
-
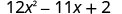
Y a-t-il un GCF ? Non S'agit-il d'un binôme, d'un trinôme ou
existe-t-il plus de trois termes ?Trinomial. Les carrés a et c sont-ils parfaits ? Non, a = 12, ce
n'est pas un carré parfait.Utilisez des essais et des erreurs ou la méthode « ac ».
Nous utiliserons ici des essais et des erreurs.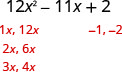
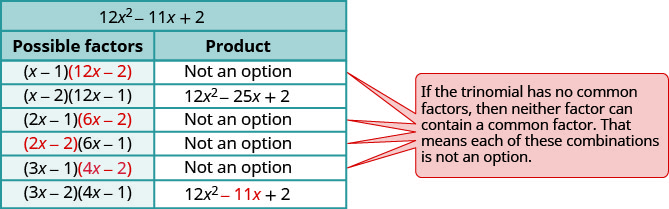
- Vérifiez. \(\begin{array}{l}{(3 x-2)(4 x-1)} \\ {12 x^{2}-3 x-8 x+2} \\ {12 x^{2}-11 x+2 }\checkmark \end{array}\)
Facteur complet :\(10 a^{2}-17 a+6\)
- Réponse
-
\((5 a-6)(2 a-1)\)
Facteur complet :\(8 x^{2}-18 x+9\)
- Réponse
-
\((2 x-3)(4 x-3)\)
Facteur complet :\(g^{3}+25 g\)
- Réponse
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, g.} &g^{3}+25 g \\\text { Factor out the GCF. } & &g\left(g^{2}+25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \quad \text { Is it a sum? Of squares? } & \text { Yes. } & \text { Sums of squares are prime. } \\\text { Check. } \\ \\ \quad \text { Is the expression factored completely? } &\text { Yes. } \\ \quad \text { Multiply. } \\ \qquad \begin{array}{l}{g\left(g^{2}+25\right)} \\ {g^{3}+25 g }\checkmark \end{array} \end{array}\)
Facteur complet :\(x^{3}+36 x\)
- Réponse
-
\(x\left(x^{2}+36\right)\)
Facteur complet :\(27 y^{2}+48\)
- Réponse
-
3\(\left(9 y^{2}+16\right)\)
Facteur complet :\(12 y^{2}-75\)
- Réponse
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 3.} &12 y^{2}-75 \\\text { Factor out the GCF. } & &3\left(4 y^{2}-25\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } &\text { Binomial. } & \\ \text { Is it a sum?} & \text { No. } & \\ \text { Is it a difference? Of squares or cubes? } &\text { Yes, squares. } & 3\left((2 y)^{2}-(5)^{2}\right) \\ \text { Write as a product of conjugates. } & &3(2 y-5)(2 y+5)\\\text { Check. } \\ \\ \text { Is the expression factored completely? } & \text{ Yes.}& \\ \text { Neither binomial is a difference of } \\ \text { squares. } \\ \text{ Multiply.} \\ \quad \begin{array}{l}{3(2 y-5)(2 y+5)} \\ {3\left(4 y^{2}-25\right)} \\ {12 y^{2}-75}\checkmark \end{array} \end{array}\)
Facteur complet :\(16 x^{3}-36 x\)
- Réponse
-
4\(x(2 x-3)(2 x+3)\)
Facteur complet :\(27 y^{2}-48\)
- Réponse
-
3\((3 y-4)(3 y+4)\)
Facteur complet :\(4 a^{2}-12 a b+9 b^{2}\)
- Réponse
-
Y a-t-il un GCF ? Non 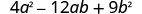
S'agit-il d'un binôme, d'un trinôme ou existe-t-il
d'autres termes ?Trinomial avec\(a\neq 1\). Mais le premier terme est un carré
parfait.Le dernier terme est-il un carré parfait ? Oui 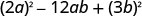
Est-ce que ça correspond au motif,\(a^{2}-2 a b+b^{2}\) ? Oui 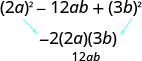
Écrivez-le sous forme de carré. 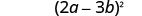
Vérifiez votre réponse. L'expression est-elle complètement prise en compte ? Oui Le binôme n'est pas une différence de carrés. Multipliez. \((2 a-3 b)^{2}\) \((2 a)^{2}-2 \cdot 2 a \cdot 3 b+(3 b)^{2}\) \(4 a^{2}-12 a b+9 b^{2} \checkmark\)
Facteur complet :\(4 x^{2}+20 x y+25 y^{2}\)
- Réponse
-
\((2 x+5 y)^{2}\)
Facteur complet :\(9 m^{2}+42 m n+49 n^{2}\)
- Réponse
-
\((3 m+7 n)^{2}\)
Facteur complet :\(6 y^{2}-18 y-60\)
- Réponse
-
\(\begin{array}{lll} \text { Is there a GCF? } & \text{Yes, 6.} &6 y^{2}-18 y-60 \\\text { Factor out the GCF. } & \text { Trinomial with leading coefficient } 1&6\left(y^{2}-3 y-10\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more terms? } & & \\ \text { "Undo' FOIL. } & 6(y\qquad )(y\qquad ) &6(y+2)(y-5) \\ \text { Check your answer. } \\ \text { Is the expression factored completely? } & & \text{ Yes.} \\ \text { Neither binomial is a difference of squares. } \\ \text { Multiply. } \\ \\\qquad \begin{array}{l}{6(y+2)(y-5)} \\ {6\left(y^{2}-5 y+2 y-10\right)} \\ {6\left(y^{2}-3 y-10\right)} \\ {6 y^{2}-18 y-60} \checkmark \end{array} \end{array}\)
Facteur complet :\(8 y^{2}+16 y-24\)
- Réponse
-
8\((y-1)(y+3)\)
Facteur complet :\(5 u^{2}-15 u-270\)
- Réponse
-
5\((u-9)(u+6)\)
Facteur complet :\(24 x^{3}+81\)
- Réponse
-
Y a-t-il un GCF ? Oui, 3. \(24 x^{3}+81\) Tenez-le en compte. 3\(\left(8 x^{3}+27\right)\) Entre parenthèses, s'agit-il d'un binôme, d'un trinôme
ou existe-t-il plus de trois termes ?Binomiale. Est-ce une somme ou une différence ? Somme. De carrés ou de cubes ? Somme de cubes. 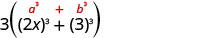
Écrivez-le en utilisant le motif de la somme des cubes. 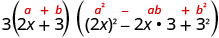
L'expression est-elle complètement prise en compte ? Oui 3\((2 x+3)\left(4 x^{2}-6 x+9\right)\) Vérifiez en multipliant. Nous vous laissons le chèque.
Facteur complet :\(250 m^{3}+432\)
- Réponse
-
2\((5 m+6)\left(25 m^{2}-30 m+36\right)\)
Facteur complet :\(81 q^{3}+192\)
- Réponse
-
\(3(3q+4)\left(9q^{2}-12 q+16\right)\)
Facteur complet :\(2 x^{4}-32\)
- Réponse
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &2 x^{4}-32 \\\text { Factor out the GCF. } & &2\left(x^{4}-16\right) \\ \text { In the parentheses, is it a binomial, trinomial, } & & \\ \text { or are there more than three terms? } & \text { Binomial. }& \\ \text { Is it a sum or difference? } &\text { Yes. }& \\\text { Of squares or cubes? } & \text { Difference of squares. } & 2\left(\left(x^{2}\right)^{2}-(4)^{2}\right) \\ \text { Write it as a product of conjugates. } & & 2\left(x^{2}-4\right)\left(x^{2}+4\right) \\ \text { The first binomial is again a difference of squares. } & & 2\left((x)^{2}-(2)^{2}\right)\left(x^{2}+4\right) \\ \text { Write it as a product of conjugates. } & & 2(x-2)(x+2)\left(x^{2}+4\right) \\ \text { Is the expression factored completely? } &\text { Yes. } & \\ \\ \text { None of these binomials is a difference of squares. } \\ \text { Check your answer. } \\ \text{ Multiply. }\\ \\ \qquad \qquad \begin{array}{l}{2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-2)(x+2)\left(x^{2}+4\right)} \\ {2(x-10)} \\ {2 x^{4}-32} \checkmark \end{array} \end{array}\)
Facteur complet :\(4 a^{4}-64\)
- Réponse
-
4\(\left(a^{2}+4\right)(a-2)(a+2)\)
Facteur complet :\(7 y^{4}-7\)
- Réponse
-
7\(\left(y^{2}+1\right)(y-1)(y+1)\)
Facteur complet :\(3 x^{2}+6 b x-3 a x-6 a b\)
- Réponse
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 3.} &3 x^{2}+6 b x-3 a x-6 a b\\\text { Factor out the GCF. } & &3\left(x^{2}+2 b x-a x-2 a b\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { More than } 3 & \\ \text { or are there more terms? } &\text { terms. } & \\ \text { Use grouping. } & & \begin{array}{c}{3[x(x+2 b)-a(x+2 b)]} \\ {3(x+2 b)(x-a)}\end{array} \\ \text { Check your answer. } \\ \\ \text { Is the expression factored completely? Yes. } \\ \text { Multiply. } \\\qquad \qquad \begin{array}{l}{3(x+2 b)(x-a)} \\ {3\left(x^{2}-a x+2 b x-2 a b\right)} \\ {3 x^{2}-3 a x+6 b x-6 a b} \checkmark \end{array}\end{array}\)
Facteur complet :\(6 x^{2}-12 x c+6 b x-12 b c\)
- Réponse
-
6\((x+b)(x-2 c)\)
Facteur complet :\(16 x^{2}+24 x y-4 x-6 y\)
- Réponse
-
2\((4 x-1)(x+3 y)\)
Facteur complet :\(10 x^{2}-34 x-24\)
- Réponse
-
\(\begin{array}{llc} \text { Is there a GCF? } & \text{Yes, 2.} &10 x^{2}-34 x-24\\\text { Factor out the GCF. } & &2\left(5 x^{2}-17 x-12\right)\\ \text { In the parentheses, is it a binomial, trinomial, } &\text { Trinomial with } & \\ \text { or are there more than three terms? } &\space a \neq 1 & \\ \text { Use trial and error or the "ac" method. } & & 2\left(5 x^{2}-17 x-12\right) \\ & & 2(5 x+3)(x-4) \\ \text { Check your answer. Is the expression factored } \\\text { completely? Yes. }\\ \\ \text { Multiply. } \\ \qquad \begin{array}{l}{2(5 x+3)(x-4)} \\ {2\left(5 x^{2}-20 x+3 x-12\right)} \\ {2\left(5 x^{2}-17 x-12\right)} \\ {10 x^{2}-34 x-24}\checkmark \end{array}\end{array}\)
Facteur complet :\(4 p^{2}-16 p+12\)
- Réponse
-
4\((p-1)(p-3)\)
Facteur complet :\(6 q^{2}-9 q-6\)
- Réponse
-
3\((q-2)(2 q+1)\)
Concepts clés
- Stratégie générale pour la factorisation des polynômes Voir la figure\(\PageIndex{1}\).
- Comment factoriser les polynômes
- Y a-t-il un plus grand facteur commun ? Tenez-le en compte.
- Le polynôme est-il binomial, trinomial ou existe-t-il plus de trois termes ?
- S'il s'agit d'un binôme :
est-ce une somme ?- Des carrés ? Les sommes des carrés ne sont pas prises en compte.
- Des cubes ? Utilisez le modèle de somme des cubes.
- Des carrés ? Facteur comme produit des conjugués.
- Des cubes ? Utilisez la différence de motif de cubes.
- S'il s'agit d'un trinôme :
est-ce de la forme\(x^{2}+b x+c\) ? Annuler FOIL.
Est-ce de la forme\(a x^{2}+b x+c\) ?- Si « a » et « c » sont des carrés, vérifiez s'ils correspondent au motif carré trinomial.
- Utilisez la méthode d'essais et d'erreurs ou la méthode « ac ».
- S'il contient plus de trois termes :
utilisez la méthode de regroupement.
- S'il s'agit d'un binôme :
- Vérifiez. Est-ce complètement pris en compte ? Les facteurs se multiplient-ils jusqu'au polynôme d'origine ?


