Skip to main content
Global

7.3 : Trinômes quadratiques factoriels avec un coefficient principal autre que 1

  1. Last updated
  2. Save as PDF
  • Page ID
    194593

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Reconnaître une stratégie préliminaire pour factoriser complètement les polynômes
    • Facteur : trinômes de la forme\(ax^{2}+bx+c\) avec un GCF
    • Trinômes factoriels par essais et erreurs
    • Trinômes factoriels utilisant la méthode « ac »
    Remarque

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Trouvez le GCF de 45\(p^{2}\) et 30\(p^{6}\)
      Si vous avez oublié ce problème, passez en revue l'exercice 7.1.4.
    2. Multipliez\((3 y+4)(2 y+5)\)
      Si vous avez oublié ce problème, passez en revue l'exercice 6.3.37.
    3. Combinez des termes similaires\(12 x^{2}+3 x+5 x+9\)
      Si vous avez oublié ce problème, passez en revue l'exercice 1.3.37.

    Reconnaître une stratégie préliminaire d'affacturage

    Résumons où nous en sommes jusqu'à présent en ce qui concerne la factorisation des polynômes. Dans les deux premières sections de ce chapitre, nous avons utilisé trois méthodes de factorisation : factoriser le GCF, factoriser par regroupement et factoriser un trinôme en « annulant » le FOIL. D'autres méthodes suivront au fur et à mesure que vous poursuivrez ce chapitre, ainsi que plus tard dans vos études d'algèbre.

    Comment saurez-vous quand utiliser chaque méthode d'affacturage ? Au fur et à mesure que vous découvrirez d'autres méthodes d'affacturage, comment saurez-vous quand appliquer chaque méthode pour ne pas les confondre ? Cela vous aidera à organiser les méthodes d'affacturage dans une stratégie qui peut vous aider à utiliser la bonne méthode.

    Lorsque vous commencez à factoriser un polynôme, demandez toujours d'abord : « Y a-t-il un facteur commun le plus important ? » Si c'est le cas, prenez-en d'abord en compte.

    La prochaine chose à considérer est le type de polynôme. Combien de termes y a-t-il ? Est-ce un binôme ? Un trinôme ? Ou comporte-t-il plus de trois mandats ?

    • S'il s'agit d'un trinôme dont le coefficient principal est un\(x^{2}+b x+c\), utilisez la méthode « undo FOIL ».
    • S'il contient plus de trois termes, essayez la méthode de regroupement. C'est la seule méthode à utiliser pour les polynômes de plus de trois termes.

    Certains polynômes ne peuvent pas être pris en compte. Ils sont appelés « premiers ». Ci-dessous, nous résumons les méthodes que nous avons utilisées jusqu'à présent.

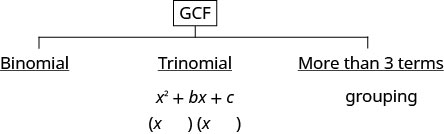
    Cette figure répertorie les stratégies de factorisation des polynômes. En haut de la figure se trouve G C F, où l'affacturage commence toujours. À partir de là, la figure comporte trois branches. Le premier est binomial, le second est trinomial de la forme x ^ 2 + b x +c, et le troisième est « plus de trois termes », étiqueté avec regroupement.

    CHOISISSEZ UNE STRATÉGIE POUR FACTORISER COMPLÈTEMENT LES POLYNÔMES.
    1. Y a-t-il un plus grand facteur commun ?
      • Tenez-le en compte.
    2. Le polynôme est-il binomial, trinomial ou existe-t-il plus de trois termes ?
      • S'il s'agit d'un binôme, nous n'avons actuellement aucune méthode pour le factoriser.
      • S'il s'agit d'un trinôme de la forme\(x^{2}+b x+c\) : Annuler le FOIL\((x\qquad)(x\qquad)\)
      • S'il contient plus de trois termes : utilisez la méthode de regroupement.
    3. Vérifiez en multipliant les facteurs.

    Utilisez la stratégie préliminaire pour factoriser complètement un polynôme. Un polynôme est complètement factorisé si, à l'exception des monômes, tous ses facteurs sont premiers.

    Exercice\(\PageIndex{1}\)

    Identifiez la meilleure méthode à utiliser pour factoriser chaque polynôme.

    1. \(6 y^{2}-72\)
    2. \(r^{2}-10 r-24\)
    3. \(p^{2}+5 p+p q+5 q\)
    Répondez à une

    \[\begin{array}{ll} &6 y^{2}-72\\ \text { Is there a greatest common factor? } & \text {Yes, 6. } \\ \text { Factor out the } 6 &6\left(y^{2}-12\right) \\ \text { Is it a binomial, trinomial, or are there } & \text {Binomial, we have no method to factor } \\ \text { more than } 3 \text { terms? } & \text {binomials yet. } \end{array} \nonumber\]

    Réponse b

    \[\begin{array}{ll} &r^{2}-10 r-24\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {Trinomial, with leading coefficient } 1, \text { so } \\ \text { more than three terms? }& \text {"undo" FOIL. }\end{array} \nonumber\]

    Réponse c

    \[\begin{array}{ll} &p^{2}+5 p+p q+5 q\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {More than three terms, so factor using }\\ \text { more than three terms? }& \text {grouping. }\end{array} \nonumber\]

    Exercice\(\PageIndex{2}\)

    Identifiez la meilleure méthode à utiliser pour factoriser chaque polynôme :

    1. \(4 y^{2}+32\)
    2. \(y^{2}+10 y+21\)
    3. \(y z+2 y+3 z+6\)
    Répondez à une

    aucune méthode

    Réponse b

    annuler avec FOIL

    Réponse c

    facteur avec regroupement

    Exercice\(\PageIndex{3}\)

    Identifiez la meilleure méthode à utiliser pour factoriser chaque polynôme :

    1. \(a b+a+4 b+4\)
    2. \(3 k^{2}+15\)
    3. \(p^{2}+9 p+8\)
    Répondez à une

    facteur utilisant le regroupement

    Réponse b

    aucune méthode

    Réponse c

    annuler avec FOIL

    Facteurs : trinômes de la forme ax 2 + bx + c avec un GCF

    Maintenant que nous avons organisé ce que nous avons couvert jusqu'à présent, nous sommes prêts à factoriser les trinômes dont le coefficient principal n'est pas 1, les trinômes de la forme\(a x^{2}+b x+c\). N'oubliez pas de toujours vérifier d'abord s'il y a un GCF ! Parfois, après avoir factorisé le GCF, le coefficient principal du trinôme devient 1 et vous pouvez le factoriser selon les méthodes décrites dans la dernière section. Faisons quelques exemples pour voir comment cela fonctionne. Faites attention aux signes des deux exemples suivants.

    Exercice\(\PageIndex{4}\)

    Facteur complètement :\(2 n^{2}-8 n-42\).

    Réponse

    Utilisez la stratégie préliminaire.

    \(\begin{array}{ll} \text { Is there a greatest common factor? }&2 n^{2}-8 n-42\\ \text { Yes, GCF }=2 . \text { Factor it out. }& 2\left(n^{2}-4 n-21\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 2(n\qquad )(n\qquad) \\ \text { Use } 3 \text { and }-7 \text { as the last terms of the binomials. } & 2(n+3)(n-7) \end{array}\)

    Facteurs de −21 Somme des facteurs
    1, −21 1+ (−21) =−20
    3, −7 3+ (−7) =−4*

    \(\begin{array}{l}{\text {Check. }} \\ {2(n+3)(n-7)} \\ {2\left(n^{2}-7 n+3 n-21\right)} \\ {2\left(n^{2}-4 n-21\right)} \\ {2 n^{2}-8 n-42 }\checkmark \end{array}\)

    Exercice\(\PageIndex{5}\)

    Facteur complet :\(4 m^{2}-4 m-8\)

    Réponse

    4\((m+1)(m-2)\)

    Exercice\(\PageIndex{6}\)

    Facteur complet :\(5 k^{2}-15 k-50\)

    Réponse

    5\((k+2)(k-5)\)

    Exercice\(\PageIndex{7}\)

    Facteur complet :\(4 y^{2}-36 y+56\)

    Réponse

    Utilisez la stratégie préliminaire.
    \(\begin{array}{ll} \text { Is there a greatest common factor? }&4 y^{2}-36 y+56\\ \text { Yes, GCF }=4 . \text { Factor it out. }&4\left(y^{2}-9 y+14\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 4(y\qquad )(y\qquad) \\\text { Use a table like the one below to find two numbers that multiply to }&\\ 14 \text { and add to }-9\\ \text { Both factors of } 14 \text { must be negative. } & 4(y-2)(y-7) \end{array}\)

    Facteurs de 14 Somme des facteurs
    −1, −14 −1+ (−14) =−15
    −2, −7 −2+ (−7) =−9*

    \(\begin{array}{l}{\text { Check. }} \\ {4(y-2)(y-7)} \\ {4\left(y^{2}-7 y-2 y+14\right)} \\ {4\left(y^{2}-9 y+14\right)} \\ {4 y^{2}-36 y+42 } \checkmark \end{array}\)

    Exercice\(\PageIndex{8}\)

    Facteur complet :\(3 r^{2}-9 r+6\)

    Réponse

    3\((r-1)(r-2)\)

    Exercice\(\PageIndex{9}\)

    Facteur complet :\(2 t^{2}-10 t+12\)

    Réponse

    2\((t-2)(t-3)\)

    Dans l'exemple suivant, le GCF inclura une variable.

    Exercice\(\PageIndex{10}\)

    Facteur complet :\(4 u^{3}+16 u^{2}-20 u\)

    Réponse

    Utilisez la stratégie préliminaire.
    \(\begin{array}{ll} \text { Is there a greatest common factor? }&4 u^{3}+16 u^{2}-20 u\\ \text { Yes, GCF }=4 u . \text { Factor it. }&4 u\left(u^{2}+4 u-5\right) \\\text { Binomial, trinomial, or more than three terms? }&\\ \text { more than three terms? }& \\ \text { It is a trinomial. So "undo FOIL." } & 4u(u\qquad )(u\qquad) \\\text { Use a table like the table below to find two numbers that }&4 u(u-1)(u+5)\\ \text { multiply to }-5 \text { and add to } 4\end{array}\)

    Facteurs de −5 Somme des facteurs
    −1,5 −1+5 = 4*
    1, −5 1+ (−5) =−4

    Vérifiez.

    \(\begin{array}{l}{4 u(u-1)(u+5)} \\ {4 u\left(u^{2}+5 u-u-5\right)} \\ {4 u\left(u^{2}+4 u-5\right)} \\ {4 u^{3}+16 u^{2}-20 u }\checkmark \end{array}\)

    Exercice\(\PageIndex{11}\)

    Facteur complet :\(5 x^{3}+15 x^{2}-20 x\)

    Réponse

    5\(x(x-1)(x+4)\)

    Exercice\(\PageIndex{12}\)

    Facteur complet :\(6 y^{3}+18 y^{2}-60 y\)

    Réponse

    6\(y(y-2)(y+5)\)

    Factor Trinomials utilisant des essais et des erreurs

    Que se passe-t-il lorsque le coefficient principal n'est pas 1 et qu'il n'y a pas de GCF ? Plusieurs méthodes peuvent être utilisées pour factoriser ces trinômes. Nous allons d'abord utiliser la méthode des essais et des erreurs.

    Prenons en compte le trinôme\(3 x^{2}+5 x+2\)

    D'après nos travaux antérieurs, nous nous attendons à ce que cela soit pris en compte dans deux binômes.

    \[\begin{array}{c}{3 x^{2}+5 x+2} \\ {( \qquad)( \qquad)}\end{array}\]

    Nous savons que les premiers termes des facteurs binomiaux se multiplieront pour nous donner 3\(x^{2}\). Les seuls facteurs de 3\(x^{2}\) sont\(1 x, 3 x\). Nous pouvons les placer dans les binômes.

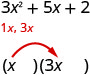
    Cette figure a pour polynôme 3 x^ 2 +5 x +2. En dessous se trouvent deux termes, 1 x et 3 x. En dessous se trouvent les deux facteurs x et (3 x) affichés multipliés.

    Vérifiez. Est-ce que\(1 x \cdot 3 x=3 x^{2}\) ?

    Nous savons que les derniers termes des binômes seront multipliés par 2. Comme ce trinôme contient tous des termes positifs, il suffit de prendre en compte les facteurs positifs. Les seuls facteurs de 2 sont 1 et 2. Mais nous avons maintenant deux cas à considérer car cela fera une différence si nous écrivons 1, 2 ou 2, 1.

    Cette figure montre les facteurs possibles du polynôme 3x^2 +5x +2. Le polynôme est écrit deux fois. Sous les deux, il y a les termes 1x, 3x sous le 3x^2. Il y a également les facteurs 1, 2 sous le terme 2. Au bas de la figure, il existe deux factorisations possibles du polynôme. Le premier est (x + 1) (3x + 2) et le suivant est (x + 2) (3x + 1).

    Quels sont les facteurs corrects ? Pour en décider, nous multiplions les termes intérieurs et extérieurs.

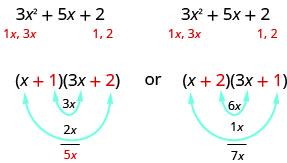
    Cette figure montre les facteurs possibles du polynôme 3 x^ 2 + 5 x +2. Le polynôme est écrit deux fois. Sous les deux, il y a les termes 1 x, 3 x sous le 3 x ^ 2. Il y a également les facteurs 1, 2 sous le terme 2. Au bas de la figure, il existe deux factorisations possibles du polynôme. Le premier est (x + 1) (3 x + 2). Sous cette factorisation se trouvent les produits 3 x résultant de la multiplication des termes intermédiaires 1 et 3 x. Il y a également le produit de 2 x résultant de la multiplication des termes extérieurs x et 2. Ces produits de 3 x et 2 x s'additionnent à 5 x. Sous la deuxième factorisation se trouvent les produits 6 x résultant de la multiplication des termes intermédiaires 2 et 3 x. Il y a également le produit de 1 x obtenu en multipliant les termes extérieurs x et 1. Ces deux produits de 6 x et 1 x s'ajoutent à 7 x.

    Puisque le terme moyen du trinôme est de 5 x, les facteurs du premier cas fonctionneront. FOIL va vérifier.

    \[\begin{array}{l}{(x+1)(3 x+2)} \\ {3 x^{2}+2 x+3 x+2} \\ {3 x^{2}+5 x+2}\checkmark \end{array}\]

    Notre résultat de l'affacturage est le suivant :

    \[\begin{array}{l}{3 x^{2}+5 x+2} \\ {(x+1)(3 x+2)}\end{array}\]

    Exercice\(\PageIndex{13}\): How to Factor Trinomials of the Form \(ax^2+bx+c\) Using Trial and Error

    Facteur complet :\(3 y^{2}+22 y+7\)

    Réponse

    Ce tableau résume les étapes de factorisation de 3 y ^ 2 + 22 y + 7. Les états de la première ligne écrivent le trinôme par ordre décroissant. Le polynôme s'écrit 3 y ^ 2 +22 y + 7.Les états de la deuxième ligne trouvent toutes les paires de facteurs du premier terme. Les seules paires répertoriées sont 1 y, 3 y. Comme il n'y a qu'une seule paire, elles se trouvent entre parenthèses écrites (1 y) et (3 y).La troisième ligne indique « Trouvez toutes les paires factoriées du troisième terme ». Il indique également que les seuls facteurs de 7 sont 1 et 7.Les états de la quatrième ligne testent toutes les combinaisons possibles de facteurs jusqu'à ce que le bon produit soit trouvé. Les facteurs possibles sont indiqués (y + 1) (3 y + 7) et (y + 7) (3y + 1). Sous chaque facteur se trouvent les produits des termes extérieurs et des termes intérieurs. Pour le premier, c'est 7 ans et 3 ans. Pour le second, c'est 21 y et y. La combinaison (y + 7) (3 y + 1) est la factorisation correcte.

    La dernière ligne indique qu'il faut vérifier en multipliant. Le produit de (y + 7) (3 y + 1) est représenté par 3 y ^ 2 + 22 y + 7.
    Exercice\(\PageIndex{14}\)

    Facteur complet :\(2 a^{2}+5 a+3\)

    Réponse

    \((a+1)(2 a+3)\)

    Exercice\(\PageIndex{15}\)

    Facteur complet :\(4 b^{2}+5 b+1\)

    Réponse

    \((b+1)(4 b+1)\)

    TRINÔMES FACTORIELS DE LA FORME\(ax^2+bx+c\) USING TRIAL AND ERROR.
    1. Écrivez le trinôme par ordre décroissant de degrés.
    2. Trouvez toutes les paires de facteurs du premier terme.
    3. Trouvez toutes les paires de facteurs du troisième terme.
    4. Testez toutes les combinaisons possibles de facteurs jusqu'à ce que le bon produit soit trouvé.
    5. Vérifiez en multipliant.

    Lorsque le terme moyen est négatif et que le dernier terme est positif, les signes des binômes doivent tous deux être négatifs.

    Exercice\(\PageIndex{16}\)

    Facteur complet :\(6 b^{2}-13 b+5\)

    Réponse
    Le trinôme est déjà dans l'ordre décroissant. .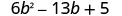
    Déterminez les facteurs du premier mandat. .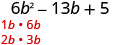
    Déterminez les facteurs du dernier trimestre. Tenez compte des signes. Depuis le dernier terme, 5 est positif, ses facteurs doivent tous deux être positifs ou négatifs. Le coefficient du moyen terme étant négatif, nous utilisons les facteurs négatifs. .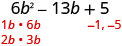
    Tenez compte de toutes les combinaisons de facteurs.
    \(6 b^{2}-13 b+5\)
    Facteurs possibles Produit
    \ (6 b^ {2} -13 b+5 \) Facteurs possibles » data-valign="top » class="lt-math-15168"> (b−1) (6b−5) \ (6 b^ {2} -13 b+5 \) Produit » data-valign="top » class="lt-math-15168">\(6 b^{2}-11 b+5\)
    \ (6 b^ {2} -13 b+5 \) Facteurs possibles » data-valign="top » class="lt-math-15168"> (b−5) (6b−1) \ (6 b^ {2} -13 b+5 \) Produit » data-valign="top » class="lt-math-15168">\(6 b^{2}-31 b+5\)
    \ (6 b^ {2} -13 b+5 \) Facteurs possibles » data-valign="top » class="lt-math-15168"> (2b−1) (3b−5) \ (6 b^ {2} -13 b+5 \) Produit » data-valign="top » class="lt-math-15168">\(6 b^{2}-13 b+5\) *
    \ (6 b^ {2} -13 b+5 \) Facteurs possibles » data-valign="top » class="lt-math-15168"> (2b−5) (3b−1) \ (6 b^ {2} -13 b+5 \) Produit » data-valign="top » class="lt-math-15168">\(6 b^{2}-17 b+5\)
    \(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 b-1)(3 b-5)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 v}\checkmark \end{array}\end{array}\)
    Exercice\(\PageIndex{17}\)

    Facteur complet :\(8 x^{2}-14 x+3\)

    Réponse

    \((2 x-3)(4 x-1)\)

    Exercice\(\PageIndex{18}\)

    Facteur complet :\(10 y^{2}-37 y+7\)

    Réponse

    \((2 y-7)(5 y-1)\)

    Lorsque nous factorisons une expression, nous cherchons toujours d'abord le plus grand facteur commun. Si l'expression n'a pas de plus grand facteur commun, il ne peut pas non plus y en avoir un dans ses facteurs. Cela peut nous aider à éliminer certaines des combinaisons de facteurs possibles.

    Exercice\(\PageIndex{19}\)

    Facteur complet :\(14 x^{2}-47 x-7\)

    Réponse
    Le trinôme est déjà dans l'ordre décroissant. .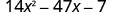
    Déterminez les facteurs du premier mandat. .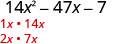
    Déterminez les facteurs du dernier trimestre. Tenez compte des signes. Comme il est négatif, un facteur doit être positif et un facteur négatif. .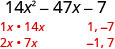
    Tenez compte de toutes les combinaisons de facteurs. Nous utilisons chaque paire de facteurs de 14\(x^{2}\) avec chaque paire de facteurs de −7.
    Facteurs de\(14x^2\) Associez avec Facteurs de −7
    \ (14x^2 \) » validation des données = « top » class="lt-math-15168">\(x, 14 x\)   11, −7
    −7, 11
    (ordre inverse)
    \ (14x^2 \) » validation des données = « top » class="lt-math-15168">\(x, 14 x\)   −1, 77
    77, −1
    (ordre inverse)
    \ (14x^2 \) » validation des données = « top » class="lt-math-15168">\(2x,7x\)   11, −7
    −7, 11
    (ordre inverse)
    \ (14x^2 \) » validation des données = « top » class="lt-math-15168">\(2x,7x\)   −1, 77
    77, −1
    (ordre inverse)

    Ces appariements mènent aux huit combinaisons suivantes.

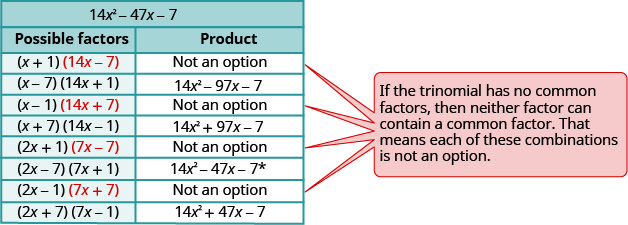
    Le titre de ce tableau est 14 x ^ 2 — 47 x moins 7. Ce tableau comporte deux colonnes. La première colonne est intitulée « Facteurs possibles » et la deuxième colonne est intitulée « produit ». La première colonne répertorie toutes les combinaisons de facteurs possibles et la deuxième colonne contient les produits. Dans la première rangée, sous « Facteurs possibles », on peut lire (x+1) et (14 x moins 7). Sous produit, dans la colonne suivante, il est indiqué « pas une option ». Dans la rangée suivante, il apparaît (x moins 7) et (14 x plus 1). Dans la rangée suivante, il apparaît (x moins 1) et (14 x plus 7). À côté de cela, dans la colonne des produits, il est indiqué « pas une option ». La rangée suivante, sous « facteurs possibles », contient l'équation (x plus 7 et 14 x moins 1). À côté de cela, dans la colonne des produits, il y a 14 x ^2 plus 97 x moins 7. La rangée suivante, sous la rubrique des facteurs possibles, contient 2 x plus 1 et 7 x moins 7. À côté de cela, dans la colonne des produits, il est écrit « pas une option ». La ligne suivante indique 2 x moins 7 et 7x plus 1. À côté de cela, dans la colonne des produits, il y a 14 x ^2 moins 47 x moins 7 avec un astérisque après le 7. La ligne suivante indique 2 x moins 1 et 7 x plus 7. À côté de cela, dans la colonne du produit, il est écrit « pas une option ». La dernière rangée indique 2 x plus 7 et 7 x moins 1. À côté de cela, dans la colonne des produits, il est indiqué 14, x, ^ 2 plus 47 x moins 7. À côté du tableau se trouve une boîte contenant quatre flèches pointant vers chaque ligne « pas une option ». La raison donnée dans la zone de texte est « si le trinôme n'a pas de facteurs communs, aucun des deux facteurs ne peut contenir de facteur commun. Cela signifie que chacune de ces combinaisons n'est pas une option. »
    \(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 x-7)(7 x+1)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 }\checkmark \end{array}\end{array}\)
    Exercice\(\PageIndex{20}\)

    Facteur complet :\(8 a^{2}-3 a-5\)

    Réponse

    \((a-1)(8 a+5)\)

    Exercice\(\PageIndex{21}\)

    Facteur complet :\(6 b^{2}-b-15\)

    Réponse

    \((2 b+3)(3 b-5)\)

    Exercice\(\PageIndex{22}\)

    Facteur complet :\(18 n^{2}-37 n+15\)

    Réponse
    Le trinôme est déjà dans l'ordre décroissant. \(18 n^{2}-37 n+15\)
    Déterminez les facteurs du premier mandat. .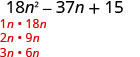
    Déterminez les facteurs du dernier trimestre. Tenez compte des signes. Comme 15 est positif et que le coefficient du moyen terme est négatif, nous utilisons les facteurs négatifs. .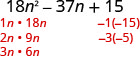

    Tenez compte de toutes les combinaisons de facteurs.

    Ce tableau a pour titre 18 n ^ 2 — 37n + 15. Ce tableau comporte deux colonnes. La première colonne est intitulée Facteurs possibles et la deuxième colonne est étiquetée produit. La première colonne répertorie toutes les combinaisons de facteurs possibles et la deuxième colonne contient les produits. Huit lignes indiquent que le produit n'est pas une option. Une zone de texte indique la raison pour laquelle aucune option n'est disponible. La raison indiquée dans la zone de texte est « si le trinôme n'a pas de facteurs communs, aucun des deux facteurs ne peut contenir de facteur commun ». La ligne contenant les facteurs (2n — 3) (9n — 5) avec le produit 18n^2 moins 37 n + 15 est précédée d'un astérisque.
    \(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 n-3)(9 n-5)\\\\\text {Check by multiplying. } \\\\ \begin{array}{l}{(2 n-3)(9 n-5)} \\ {18 n^{2}-10 n-27 n+15} \\ {18 n^{2}-37 n+15 } \checkmark\end{array} \end{array}\)
    Exercice\(\PageIndex{23}\)

    Facteur complet :\(18 x^{2}-3 x-10\)

    Réponse

    \((3 x+2)(6 x-5)\)

    Exercice\(\PageIndex{24}\)

    Facteur complet :\(30 y^{2}-53 y-21\)

    Réponse

    \((3 y+1)(10 y-21)\)

    N'oubliez pas de rechercher d'abord un GCF.

    Exercice\(\PageIndex{25}\)

    Facteur complet :\(10 y^{4}+55 y^{3}+60 y^{2}\)

    Réponse
      \(10 y^{4}+55 y^{3}+60 y^{2}\)
    Remarquez le plus grand facteur commun et considérez-le d'abord. 5\(y^{2}\left(2 y^{2}+11 y+12\right)\)
    Tenez compte du trinôme. .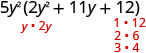

    Tenez compte de toutes les combinaisons.

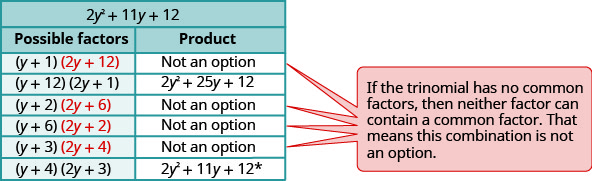
    Ce tableau a pour titre 2 y au carré + 11 y + 12. Ce tableau comporte deux colonnes. La première colonne est intitulée « Facteurs possibles » et la deuxième colonne est intitulée « produit ». La première colonne répertorie toutes les combinaisons de facteurs possibles et la deuxième colonne contient les produits. Quatre lignes indiquent que le produit n'est pas une option. Une zone de texte indique la raison pour laquelle aucune option n'est disponible. La raison indiquée dans la zone de texte est « si le trinôme n'a pas de facteurs communs, aucun des deux facteurs ne peut contenir de facteur commun ». La ligne contenant les facteurs (y + 4) (2y + 3) avec le produit 2 y au carré + 11 y + 12 est marquée d'un astérisque.
    \(\begin{array}{ll}\text{The correct factors are those whose product} &5 y^{2}(y+4)(2 y+3) \\ \text{is the original trinomial. Remember to include} & \\\text {the factor } 5 y^{2}\\\text {Check by multiplying. } \\\\ \begin{array}{l}{5 y^{2}(y+4)(2 y+3)} \\ {5 y^{2}\left(2 y^{2}+8 y+3 y+12\right)} \\ {10 y^{4}+55 y^{3}+60 y^{2}}\checkmark\end{array} \end{array}\)
    Exercice\(\PageIndex{26}\)

    Facteur complet :\(15 n^{3}-85 n^{2}+100 n\)

    Réponse

    5\(n(n-4)(3 n-5)\)

    Exercice\(\PageIndex{27}\)

    Facteur complet :\(56 q^{3}+320 q^{2}-96 q\)

    Réponse

    8\(q(q+6)(7 q-2)\)

    Trinômes factoriels utilisant la méthode « ac »

    Une autre façon de factoriser les trinômes de la forme\(ax^2+bx+c\) est la méthode « ac ». (La méthode « ac » est parfois appelée méthode de regroupement.) La méthode « ac » est en fait une extension des méthodes que vous avez utilisées dans la dernière section pour factoriser les trinômes dont le coefficient principal est un. Cette méthode est très structurée (c'est-à-dire étape par étape), et elle fonctionne toujours !

    Exercice\(\PageIndex{28}\): How to Factor Trinomials Using the “ac” Method

    Facteur :\(6 x^{2}+7 x+2\)

    Réponse

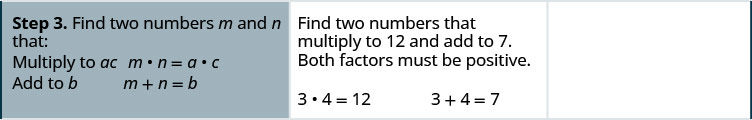
    Ce tableau répertorie les étapes à suivre pour factoriser 6 x ^ 2 + 7 x + 2. La première étape consiste à factoriser le GCF. Ce polynôme n'en possède aucun.La deuxième ligne indique de trouver le produit a c. Ensuite, elle indique a c comme suit : 6 fois 2 = 12.La troisième étape consiste à trouver deux nombres m et n dans lesquels m fois n = a c et m + n = b. La colonne du milieu se lit comme suit : « Trouvez deux nombres qui s'additionnent à 7. Les deux facteurs doivent être positifs ». Les nombres sont 3 et 4. 3 fois 4 vaut 12 et 3 + 4 vaut 7.L'étape suivante consiste à diviser le terme moyen en utilisant m et n. C'est-à-dire à écrire 7 x sous la forme 3 x + 4 x. Par conséquent, 6 x ^ 2 + 7 x + 2 est réécrit en 6 x ^ 2 +3 x + 4 x + 2.L'étape suivante consiste à factoriser par regroupement. 3 x (2 x + 1) + 2 (2 x + 1) puis factoriser à nouveau (2 x + 1) (3 x + 2).La dernière étape consiste à vérifier en multipliant. Multipliez les facteurs (2 x + 1) (3 x + 2) pour obtenir 6 x ^ 2 + 7 x + 2.

    Exercice\(\PageIndex{29}\)

    Facteur :\(6 x^{2}+13 x+2\)

    Réponse

    \((x+2)(6 x+1)\)

    Exercice\(\PageIndex{30}\)

    Facteur :\(4 y^{2}+8 y+3\)

    Réponse

    \((2 y+1)(2 y+3)\)

    FACTORISEZ LES TRINÔMES DE LA FORME EN UTILISANT LA MÉTHODE « AC ».
    1. Tenez compte de tout GCF.
    2. Trouvez le produit ac.
    3. Trouvez deux nombres m et n qui :
      \(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
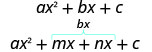
    4. Divisez le terme moyen en utilisant m et n :Cette figure montre deux équations. L'équation du haut se lit a fois x au carré plus b fois x plus c. En dessous, se trouve l'équation a fois x au carré plus m fois x plus n fois x plus c. Au-dessus des m fois x plus n fois x se trouve une parenthèse avec b fois x au-dessus.
    5. Facteur par regroupement.
    6. Vérifiez en multipliant les facteurs.

    Lorsque le troisième terme du trinôme est négatif, les facteurs du troisième terme auront des signes opposés.

    Exercice\(\PageIndex{31}\)

    Facteur :\(8 u^{2}-17 u-21\)

    Réponse
    Y a-t-il un plus grand facteur commun ? Non.   .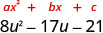
    Trouvez\(a\cdot c\) \(a\cdot c\)  
      8 (−21)  
      −168

    Trouvez deux nombres qui se multiplient par −168 et qui s'ajoutent à −17. Le facteur le plus important doit être négatif.

    Facteurs de −168 Somme des facteurs
    1, −168 1+ (−168) =−167
    2, −84 2+ (−84) =−82
    3, −56 3+ (−56) =−53
    4, −42 4+ (−42) =−38
    6, −28 6+ (−28) =−22
    7, −24 7+ (−24) =−17*
    8, −21 8+ (−21) =−13

    \(\begin{array}{lc}\text { Split the middle term using } 7 u \text { and }-24 u &8 u^{2}-17 u-21 \\ & \qquad\space \swarrow\searrow \\ & \underbrace{8 u^{2}+7 u} \underbrace{-24 u-21} \\ \text { Factor by grouping. } & u(8 u+7)-3(8 u+7) \\ & (8 u+7)(u-3) \\ \text { Check by multiplying. } & \begin{array}{l}{(8 u+7)(u-3)} \\ {8 u^{2}-24 u+7 u-21} \\ {8 u^{2}-17 u-21} \checkmark \end{array} \end{array}\)

    Exercice\(\PageIndex{32}\)

    Facteur :\(20 h^{2}+13 h-15\)

    Réponse

    \((4 h-5)(5 h+3)\)

    Exercice\(\PageIndex{33}\)

    Facteur :\(6 g^{2}+19 g-20\)

    Réponse

    \((q+4)(6 q-5)\)

    Exercice\(\PageIndex{34}\)

    Facteur :\(2 x^{2}+6 x+5\)

    Réponse
    Y a-t-il un plus grand facteur commun ? Non. .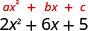
    Trouvez a⋅c a⋅c
      (25)
      10

    Trouvez deux nombres qui se multiplient par 10 et additionnent jusqu'à 6.

    Facteurs de 10 Somme des facteurs
    1,10 1+10 = 11
    2, 5 2+5 = 7

    Aucun facteur ne se multiplie par 10 et s'additionne à 6. Le polynôme est premier.

    Exercice\(\PageIndex{35}\)

    Facteur :\(10 t^{2}+19 t-15\)

    Réponse

    \((2 t+5)(5 t-3)\)

    Exercice\(\PageIndex{36}\)

    Facteur :\(3 u^{2}+8 u+5\)

    Réponse

    \((u+1)(3 u+5)\)

    N'oubliez pas de rechercher un facteur commun !

    Exercice\(\PageIndex{37}\)

    Facteur :\(10 y^{2}-55 y+70\)

    Réponse
    Y a-t-il un plus grand facteur commun ? Oui. Le GCF est de 5. .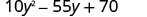
    Tenez-le en compte. Veillez à maintenir le facteur 5 tout au long de la solution ! .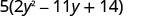
    Le trinôme entre parenthèses a un coefficient principal qui n'est pas 1. .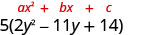
    Tenez compte du trinôme. .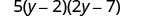
    Vérifiez en multipliant les trois facteurs.  
    5\(\left(2 y^{2}-2 y-4 y+14\right)\)  
    5\(\left(2 y^{2}-11 y+14\right)\)  
    \(10 y^{2}-55 y+70\)✓
    Exercice\(\PageIndex{38}\)

    Facteur :\(16 x^{2}-32 x+12\)

    Réponse

    4\((2 x-3)(2 x-1)\)

    Exercice\(\PageIndex{39}\)

    Facteur :\(18 w^{2}-39 w+18\)

    Réponse

    3\((3 w-2)(2 w-3)\)

    Nous pouvons maintenant mettre à jour la stratégie de factorisation préliminaire, comme indiqué dans la figure\(\PageIndex{1}\) et détaillée dans Choisir une stratégie pour factoriser complètement les polynômes (mise à jour), afin d'inclure les trinômes de la forme\(a x^{2}+b x+c\). N'oubliez pas que certains polynômes sont premiers et ne peuvent donc pas être pris en compte.

    Cette figure présente la stratégie de factorisation des polynômes. En haut de la figure se trouve le GCF. En dessous, il y a trois options. Le premier est binomial. Le second est trinomial. Sous trinomial, il y a x au carré + b x + c et a x au carré + b x +c. Les deux méthodes utilisées ici sont les essais et les erreurs et la méthode « a c ». La troisième option concerne plus de trois mandats. C'est un regroupement.
    Figurine\(\PageIndex{1}\)
    CHOISISSEZ UNE STRATÉGIE POUR FACTORISER COMPLÈTEMENT LES POLYNÔMES (MISE À JOUR).
    1. Y a-t-il un plus grand facteur commun ?
      • Tenez-le en compte.
    2. Le polynôme est-il binomial, trinomial ou existe-t-il plus de trois termes ?
      • S'il s'agit d'un binôme, nous n'avons actuellement aucune méthode pour le factoriser.
      • S'il s'agit d'un trinôme de la forme\(x^{2}+b x+c\)
        Undo FOIL \\((x\qquad)(x\qquad)\).
      • S'il s'agit d'un trinôme de la forme\(a x^{2}+b x+c\)
        Utiliser des essais et des erreurs ou la méthode « ac ».
      • S'il contient plus de trois termes,
        utilisez la méthode de regroupement.
    3. Vérifiez en multipliant les facteurs.
    Remarque

    Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur la factorisation des trinômes du formulaire\(a x^{2}+b x+c\)

    Concepts clés

    • Facteur des trinômes du\(a x^{2}+b x+c\) formulaire par essais et erreurs : voir exemple.
      1. Écrivez le trinôme par ordre décroissant de degrés.
      2. Trouvez toutes les paires de facteurs du premier terme.
      3. Trouvez toutes les paires de facteurs du troisième terme.
      4. Testez toutes les combinaisons possibles de facteurs jusqu'à ce que le bon produit soit trouvé.
      5. Vérifiez en multipliant.
    • Facteur des trinômes du formulaire\(a x^{2}+b x+c\) à l'aide de la méthode « ac » : voir exemple.
      1. Tenez compte de tout GCF.
      2. Trouvez le produit ac.
      3. Trouvez deux nombres m et n qui :\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
      4. Divisez le terme moyen en utilisant m et n :
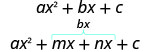
        Cette figure montre deux équations. L'équation du haut se lit a fois x au carré plus b fois x plus c. En dessous, se trouve l'équation a fois x au carré plus m fois x plus n fois x plus c. Au-dessus des m fois x plus n fois x se trouve une parenthèse avec b fois x au-dessus.
      5. Facteur par regroupement.
      6. Vérifiez en multipliant les facteurs.
    • Choisissez une stratégie pour factoriser complètement les polynômes (mise à jour) :
      1. Y a-t-il un plus grand facteur commun ? Tenez-le en compte.
      2. Le polynôme est-il binomial, trinomial ou existe-t-il plus de trois termes ?
        S'il s'agit d'un binôme, nous n'avons actuellement aucune méthode pour le factoriser.
        S'il s'agit d'un trinôme de la forme\(x^2+bx+c\)
        Undo FOIL\((x\qquad)(x\qquad)\).
        S'il s'agit d'un trinôme de la forme\(ax^2+bx+c\)
        Utiliser des essais et des erreurs ou la méthode « ac ».
        S'il contient plus de trois termes,
        utilisez la méthode de regroupement.
      3. Vérifiez en multipliant les facteurs.

    Lexique

    polynômes premiers
    Les polynômes qui ne peuvent pas être factorisés sont des polynômes premiers.