6.1 : Ajouter et soustraire des polynômes
- Page ID
- 195124
À la fin de cette section, vous serez en mesure de :
- Identifier les polynômes, les monômes, les binômes et les trinômes
- Déterminer le degré de polynômes
- Ajouter et soustraire des monômes
- Ajouter et soustraire des polynômes
- Evaluer un polynôme pour une valeur donnée
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(8x+3x\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.3.37. - Soustraire :\((5n+8)−(2n−1)\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.52. - Écrivez sous forme développée :\(a^{5}\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.3.7.
Identifier les polynômes, les monômes, les binômes et les trinômes
Vous avez appris qu'un terme est une constante ou le produit d'une constante et d'une ou plusieurs variables. Quand il est de la forme\(ax^{m}\), où\(a\) est une constante et\(m\) un nombre entier, on l'appelle un monôme. Quelques exemples de monomial sont\(8,−2x^{2},4y^{3}\), et\(11z^{7}\).
Un monomial est un terme de la forme\(ax^{m}\), où\(a\) est une constante et\(m\) un nombre entier positif.
Un monomial, ou deux ou plusieurs monômes combinés par addition ou soustraction, est un polynôme. Certains polynômes ont des noms spéciaux, basés sur le nombre de termes. Un monomial est un polynôme comportant exactement un terme. Un binôme a exactement deux termes, et un trinôme a exactement trois termes. Il n'existe aucun nom spécial pour les polynômes comportant plus de trois termes.
- polynôme —Un monôme, ou deux ou plusieurs monômes combinés par addition ou soustraction, est un polynôme.
- monomial —Un polynôme comportant exactement un terme est appelé monôme.
- binomial —Un polynôme contenant exactement deux termes est appelé binôme.
- trinôme —Un polynôme comportant exactement trois termes est appelé trinôme.
Voici quelques exemples de polynômes.
\[\begin{array}{lllll}{\text { Polynomial }} & {b+1} &{4 y^{2}-7 y+2} & {4 x^{4}+x^{3}+8 x^{2}-9 x+1} \\ {\text { Monomial }} & {14} & {8 y^{2}} & {-9 x^{3} y^{5}} & {-13}\\ {\text { Binomial }} & {a+7}&{4 b-5} & {y^{2}-16}& {3 x^{3}-9 x^{2}} \\ {\text { Trinomial }} & {x^{2}-7 x+12} & {9 y^{2}+2 y-8} & {6 m^{4}-m^{3}+8 m}&{z^{4}+3 z^{2}-1} \end{array} \nonumber\]
Notez que chaque monôme, binôme et trinôme est également un polynôme. Ce ne sont que des membres spéciaux de la « famille » des polynômes et ont donc des noms spéciaux. Nous utilisons les mots monomial, binôme et trinôme pour désigner ces polynômes spéciaux et nous appelons simplement tous les autres polynômes.
Déterminez si chaque polynôme est un polynôme, un binôme, un trinôme ou un autre polynôme.
- \(4y^{2}−8y−6\)
- \(−5a^{4}b^{2}\)
- \(2x^{5}−5x^{3}−3x + 4\)
- \(13−5m^{3}\)
- q
- Réponse
-
\(\begin{array}{lll}&{\text { Polynomial }} & {\text { Number of terms }} & {\text { Type }} \\ {\text { (a) }} & {4 y^{2}-8 y-6} & {3} & {\text { Trinomial }} \\ {\text { (b) }} & {-5 a^{4} b^{2}} & {1} & {\text { Monomial }} \\ {\text { (c) }} & {2 x^{5}-5 x^{3}-9 x^{2}+3 x+4} & {5} & {\text { Ponomial }} \\ {\text { (d) }} & {13-5 m^{3}} & {2} & {\text { Binomial }} \\ {\text { (e) }} & {q} & {1} & {\text { Monomial }}\end{array}\)
Déterminez si chaque polynôme est un polynôme, un binôme, un trinôme ou un autre polynôme :
- 5b
- \(8 y^{3}-7 y^{2}-y-3\)
- \(-3 x^{2}-5 x+9\)
- \(81-4 a^{2}\)
- \(-5 x^{6}\)
- Réponse
-
- monomial
- polynomial
- trinomial
- binomiale
- monomial
Déterminez si chaque polynôme est un polynôme, un binôme, un trinôme ou un autre polynôme :
- \(27 z^{3}-8\)
- \(12 m^{3}-5 m^{2}-2 m\)
- \(\frac{5}{6}\)
- \(8 x^{4}-7 x^{2}-6 x-5\)
- \(-n^{4}\)
- Réponse
-
- binomiale
- trinomial
- monomial
- polynomial
- monomial
Déterminer le degré de polynômes
Le degré d'un polynôme et le degré de ses termes sont déterminés par les exposants de la variable. Un monôme qui n'a pas de variable, juste une constante, est un cas particulier. Le degré d'une constante est 0, c'est-à-dire qu'elle ne comporte aucune variable.
- Le degré d'un terme est la somme des exposants de ses variables.
- Le degré d'une constante est 0.
- Le degré d'un polynôme est le degré le plus élevé de tous ses termes.
Voyons comment cela fonctionne en examinant plusieurs polynômes. Nous allons procéder étape par étape, en commençant par les monômes, puis en passant aux polynômes avec plus de termes.

Un polynôme prend la forme standard lorsque les termes d'un polynôme sont écrits par ordre décroissant de degrés. Prenez l'habitude d'écrire d'abord le terme avec le diplôme le plus élevé.
Déterminez le degré des polynômes suivants.
- 10 ans
- \(4 x^{3}-7 x+5\)
- −15
- \(-8 b^{2}+9 b-2\)
- \(8 x y^{2}+2 y\)
- Réponse
-
- \(\begin{array}{ll} & 10y\\ \text{The exponent of y is one. } y=y^1 & \text{The degree is 1.}\end{array}\)
- \(\begin{array}{ll} & 4 x^{3}-7 x+5\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
- \(\begin{array}{ll} & -15\\ \text{The degree of a constant is 0.} & \text{The degree is 0.}\end{array}\)
- \(\begin{array}{ll} & -8 b^{2}+9 b-2\\ \text{The highest degree of all the terms is 2.} & \text{The degree is 2.}\end{array}\)
- \(\begin{array}{ll} & 8 x y^{2}+2 y\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
Déterminez le degré des polynômes suivants :
- −15 b
- \(10 z^{4}+4 z^{2}-5\)
- \(12 c^{5} d^{4}+9 c^{3} d^{9}-7\)
- \(3 x^{2} y-4 x\)
- −9
- Réponse
-
- 1
- 4
- 12
- 3
- 0
Déterminez le degré des polynômes suivants :
- 52
- \(a^{4} b-17 a^{4}\)
- \(5 x+6 y+2 z\)
- \(3 x^{2}-5 x+7\)
- \(-a^{3}\)
- Réponse
-
- 0
- 5
- 1
- 2
- 3
Ajouter et soustraire des monômes
Vous avez appris à simplifier des expressions en combinant des termes similaires. N'oubliez pas que les termes similaires doivent avoir les mêmes variables avec le même exposant. Puisque les monômes sont des termes, ajouter et soustraire des monômes revient à combiner des termes similaires. Si les monômes sont similaires à des termes, il suffit de les combiner en ajoutant ou en soustrayant le coefficient.
Ajoutez :\(25 y^{2}+15 y^{2}\)
- Réponse
-
\(\begin{array}{ll} & 25 y^{2}+15 y^{2}\\ \text{Combine like terms.} & 40y^{2}\end{array}\)
Ajoutez :\(12 q^{2}+9 q^{2}\)
- Réponse
-
21\(q^{2}\)
Ajoutez :\(-15 c^{2}+8 c^{2}\)
- Réponse
-
\(-7 c^{2}\)
Soustraire : 16p− (−7p)
- Réponse
-
\(\begin{array}{ll} & 16p−(−7p) \\ \text{Combine like terms.} & 23p\end{array}\)
Soustraire : 8 m− (−5 m).
- Réponse
-
13 m
Soustraire :\(-15 z^{3}-\left(-5 z^{3}\right)\)
- Réponse
-
\(-10 z^{3}\)
N'oubliez pas que les termes similaires doivent avoir les mêmes variables avec les mêmes exposants.
Simplifiez :\(c^{2}+7 d^{2}-6 c^{2}\)
- Réponse
-
\(\begin{array}{ll} & c^{2}+7 d^{2}-6 c^{2} \\ \text{Combine like terms.} & -5 c^{2}+7 d^{2} \end{array}\)
Ajoutez :\(8 y^{2}+3 z^{2}-3 y^{2}\)
- Réponse
-
\(5 y^{2}+3 z^{2}\)
Ajoutez :\(3 m^{2}+n^{2}-7 m^{2}\)
- Réponse
-
\(-4 m^{2}+n^{2}\)
Simplifiez :\(u^{2} v+5 u^{2}-3 v^{2}\)
- Réponse
-
\ (\ begin {array} {ll} &u^ {2} v+5 u^ {2} -3 v^ {2}
\ \ text {Il n'existe aucun terme similaire à combiner.} & u^ {2} v+5 u^ {2} -3 v^ {2} \ end {tableau} \)
Simplifiez :\(m^{2} n^{2}-8 m^{2}+4 n^{2}\)
- Réponse
-
Il n'y a pas de termes similaires à combiner.
Simplifiez :\(p q^{2}-6 p-5 q^{2}\)
- Réponse
-
Il n'y a pas de termes similaires à combiner.
Ajouter et soustraire des polynômes
On peut penser que l'addition et la soustraction de polynômes se résument à l'addition et à la soustraction d'une série de monômes. Recherchez les termes similaires, c'est-à-dire ceux qui contiennent les mêmes variables et le même exposant. La propriété commutative nous permet de réorganiser les termes pour réunir des termes similaires.
Trouvez la somme :\(\left(5 y^{2}-3 y+15\right)+\left(3 y^{2}-4 y-11\right)\)
- Réponse
-
Identifiez les termes similaires. 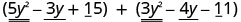
Réorganisez pour réunir les termes similaires. 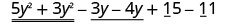
Combinez les mêmes termes. 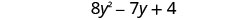
Trouvez la somme :\(\left(7 x^{2}-4 x+5\right)+\left(x^{2}-7 x+3\right)\)
- Réponse
-
\(8 x^{2}-11 x+1\)
Trouvez la somme :\(\left(14 y^{2}+6 y-4\right)+\left(3 y^{2}+8 y+5\right)\)
- Réponse
-
\(17 y^{2}+14 y+1\)
Trouvez la différence :\(\left(9 w^{2}-7 w+5\right)-\left(2 w^{2}-4\right)\)
- Réponse
-
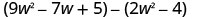
Distribuez et identifiez les termes similaires. 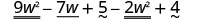
Réorganisez les termes. 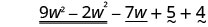
Combinez les mêmes termes. 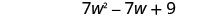
Trouvez la différence :\(\left(8 x^{2}+3 x-19\right)-\left(7 x^{2}-14\right)\)
- Réponse
-
\(15 x^{2}+3 x-5\)
Trouvez la différence :\(\left(9 b^{2}-5 b-4\right)-\left(3 b^{2}-5 b-7\right)\)
- Réponse
-
\(6 b^{2}+3\)
Soustraire :\(\left(c^{2}-4 c+7\right)\) de\(\left(7 c^{2}-5 c+3\right)\)
- Réponse
-
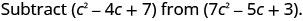
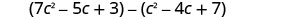
Distribuez et identifiez les termes similaires. 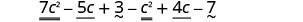
Réorganisez les termes. 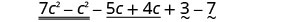
Combinez les mêmes termes. 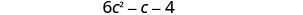
Soustraire :\(\left(5 z^{2}-6 z-2\right)\) de\(\left(7 z^{2}+6 z-4\right)\)
- Réponse
-
\(2 z^{2}+12 z-2\)
Soustraire :\(\left(x^{2}-5 x-8\right)\) de\(\left(6 x^{2}+9 x-1\right)\)
- Réponse
-
\(5 x^{2}+14 x+7\)
Trouvez la somme :\(\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)\)
- Réponse
-
\(\begin{array} {ll} & {\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)} \\\text{Distribute.} & {u^{2}-6 u v+5 v^{2}+3 u^{2}+2 u v} \\ \text{Rearrange the terms, to put like terms together} & {u^{2}+3 u^{2}-6 u v+2 u v+5 v^{2}} \\ \text{Combine like terms.} & {4 u^{2}-4 u v+5 v^{2}}\end{array}\)
Trouvez la somme :\(\left(3 x^{2}-4 x y+5 y^{2}\right)+\left(2 x^{2}-x y\right)\)
- Réponse
-
\(5 x^{2}-5 x y+5 y^{2}\)
Trouvez la somme :\(\left(2 x^{2}-3 x y-2 y^{2}\right)+\left(5 x^{2}-3 x y\right)\)
- Réponse
-
\(7 x^{2}-6 x y-2 y^{2}\)
Trouvez la différence :\(\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)\)
- Réponse
-
\(\begin{array}{ll} & {\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)} \\ \text{Distribute.} &{p^{2}+q^{2}-p^{2}-10 p q+2 q^{2}} \\\text{Rearrange the terms, to put like terms together} & {p^{2}-p^{2}-10 p q+q^{2}+2 q^{2}} \\\text{Combine like terms.} & {-10 p q+3 q^{2}}\end{array}\)
Trouvez la différence :\(\left(a^{2}+b^{2}\right)-\left(a^{2}+5 a b-6 b^{2}\right)\)
- Réponse
-
\(-5 a b-5 b^{2}\)
Trouvez la différence :\(\left(m^{2}+n^{2}\right)-\left(m^{2}-7 m n-3 n^{2}\right)\)
- Réponse
-
\(4 n^{2}+7 m n\)
Simplifiez :\(\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)\)
- Réponse
-
\(\begin{array}{ll } & {\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)} \\ \text{Distribute.} &{a^{3}-a^{2} b-a b^{2}-b^{3}+a^{2} b+a b^{2}} \\ \text{Rearrange the terms, to put like terms together} & {a^{3}-a^{2} b+a^{2} b-a b^{2}+a b^{2}-b^{3}} \\ \text{Combine like terms.} &{a^{3}-b^{3}}\end{array}\)
Simplifiez :\(\left(x^{3}-x^{2} y\right)-\left(x y^{2}+y^{3}\right)+\left(x^{2} y+x y^{2}\right)\)
- Réponse
-
\(x^{3}-y^{3}\)
Simplifiez :\(\left(p^{3}-p^{2} q\right)+\left(p q^{2}+q^{3}\right)-\left(p^{2} q+p q^{2}\right)\)
- Réponse
-
\(p^{3}-2 p^{2} q+q^{3}\)
Evaluer un polynôme pour une valeur donnée
Nous avons déjà appris à évaluer les expressions. Les polynômes étant des expressions, nous allons suivre les mêmes procédures pour évaluer un polynôme. Nous allons remplacer la valeur donnée par la variable, puis simplifier en utilisant l'ordre des opérations.
Évaluez\(5x^{2}−8x+4\) quand
- x=4
- x=−2
- x=0
- Réponse
-
1. x=4 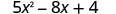

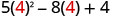
Simplifiez les exposants. 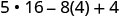
Multipliez. 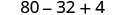
Simplifiez. 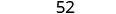
2. x=−2 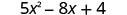

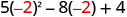
Simplifiez les exposants. 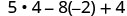
Multipliez. 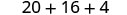
Simplifiez. 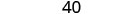
3. x=0 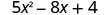

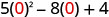
Simplifiez les exposants. 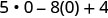
Multipliez. 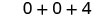
Simplifiez. 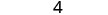
Évaluer :\(3x^{2}+2x−15\) quand
- x=3
- x=−5
- x=0
- Réponse
-
- 18
- 50
- −15
Évaluer :\(5z^{2}−z−4\) quand
- z=−2
- z=0
- z=2
- Réponse
-
- 18
- −4
- 14
Le polynôme\(−16t^{2}+250\) donne la hauteur d'une balle tt secondes après qu'elle soit tombée d'un bâtiment de 250 pieds de haut. Détermine la hauteur après t=2 secondes.
- Réponse
-
\(\begin{array}{ll } & −16t^{2}+250 \\ \text{Substitute t = 2.} & -16(2)^{2} + 250 \\ \text{Simplify }& −16\cdot 4+250 \\ \text{Simplify }& -64 + 250\\ \text{Simplify }& 186 \\& \text{After 2 seconds the height of the ball is 186 feet. } \end{array}\)
Le polynôme\(−16t^{2}+250\) donne la hauteur d'une balle tt secondes après qu'elle soit tombée d'un bâtiment de 250 pieds de haut. Détermine la hauteur après t=0 secondes.
- Réponse
-
250
Le polynôme\(−16t^{2}+250\) donne la hauteur d'une balle tt secondes après qu'elle soit tombée d'un bâtiment de 250 pieds de haut. Détermine la hauteur après t=3 secondes.
- Réponse
-
106
Le polynôme\(6x^{2}+15xy\) donne le coût, en dollars, de la production d'un conteneur rectangulaire dont le haut et le bas sont des carrés de côté x pieds et de côtés de hauteur y pieds. Déterminez le coût de production d'une boîte avec x=4 pieds et y=6y=6 pieds.
- Réponse
-
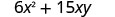
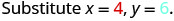
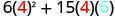
Simplifiez. 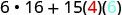
Simplifiez. 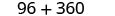
Simplifiez. 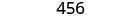
Le coût de production de la boîte est de 456$.
Le polynôme\(6x^{2}+15xy\) donne le coût, en dollars, de la production d'un conteneur rectangulaire dont le haut et le bas sont des carrés de côté x pieds et de côtés de hauteur y pieds. Déterminez le coût de production d'une boîte avec x = 6 pieds et y = 4 pieds.
- Réponse
-
576$
Le polynôme\(6x^{2}+15xy\) donne le coût, en dollars, de la production d'un conteneur rectangulaire dont le haut et le bas sont des carrés de côté x pieds et de côtés de hauteur y pieds. Déterminez le coût de production d'une boîte avec x = 5 pieds et y = 8 pieds.
- Réponse
-
750$
Concepts clés
- Monomiaux
- Un monomial est un terme de la forme\(ax^{m}\), où aa est une constante et mm est un nombre entier
- Un monomial est un terme de la forme\(ax^{m}\), où aa est une constante et mm est un nombre entier
- Polynômes
- polynôme —Un monomial, ou deux ou plusieurs monômes combinés par addition ou soustraction, est un polynôme.
- monomial —Un polynôme comportant exactement un terme est appelé monôme.
- binomial —Un polynôme contenant exactement deux termes est appelé binôme.
- trinôme —Un polynôme comportant exactement trois termes est appelé trinôme.
- Degré d'un polynôme
- Le degré d'un terme est la somme des exposants de ses variables.
- Le degré d'une constante est 0.
- Le degré d'un polynôme est le degré le plus élevé de tous ses termes.
Lexique
- binomiale
- Un binôme est un polynôme comportant exactement deux termes.
- degré d'une constante
- Le degré de n'importe quelle constante est 0.
- degré d'un polynôme
- Le degré d'un polynôme est le degré le plus élevé de tous ses termes.
- degré d'un terme
- Le degré d'un terme est l'exposant de sa variable.
- monomial
- Un monomial est un terme de la forme\(ax^m\), où a est une constante et m est un nombre entier ; un monôme possède exactement un terme.
- polynomial
- Un polynôme est un monomial, ou deux ou plusieurs monômes combinés par addition ou soustraction.
- formulaire standard
- Un polynôme prend la forme standard lorsque les termes d'un polynôme sont écrits par ordre décroissant de degrés.
- trinomial
- Un trinôme est un polynôme comportant exactement trois termes.


