4.4 : Comprendre la pente d'une droite

Last updated
Save as PDF

Page ID: 194725

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :
Utiliser des géoboards pour modéliser la pente
$m = \frac{\text{rise}}{\text{run}}$Sert à déterminer la pente d'une droite à partir de son graphique
Trouvez la pente des lignes horizontales et verticales
Utilisez la formule de pente pour déterminer la pente d'une droite entre deux points
Tracez une droite en fonction d'un point et de la pente
Résolvez les applications

Remarque

Avant de commencer, répondez à ce questionnaire de préparation.

Simplifiez :$\frac{1 - 4}{8 - 2}$.
Si vous avez oublié ce problème, passez en revue l'exercice 1.6.31
Diviser :$\frac{0}{4}, \frac{4}{0}$.
Si vous avez oublié ce problème, passez en revue l'exercice 1.10.16.
Simplifiez :$\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}$.
Si vous avez oublié ce problème, passez en revue l'exercice 1.6.4.

Lorsque vous tracez des équations linéaires, vous remarquerez peut-être que certaines lignes s'inclinent vers le haut lorsqu'elles vont de gauche à droite et que d'autres s'inclinent vers le bas. Certaines lignes sont très raides et d'autres plus plates. Qu'est-ce qui détermine si une ligne est inclinée vers le haut ou vers le bas ou si elle est raide ou plate ?

En mathématiques, « l'inclinaison » d'une ligne s'appelle la pente de la ligne. Le concept de pente a de nombreuses applications dans le monde réel. L'inclinaison d'un toit, la pente d'une autoroute et une rampe pour fauteuil roulant sont des exemples d'endroits où l'on voit littéralement des pentes. Et lorsque vous faites du vélo, vous sentez la pente lorsque vous montez ou descendez la côte.

Dans cette section, nous allons explorer le concept de pente.

Utiliser des géoboards pour modéliser la pente

Un géoboard est un tableau sur lequel se trouve une grille de piquets. L'utilisation d'élastiques sur un géoboard nous permet de modéliser des lignes sur une grille de coordonnées de manière concrète. En étirant un élastique entre deux piquets sur un géoboard, nous pouvons découvrir comment déterminer la pente d'une ligne.

L'activité de mathématiques manipulatrices « Exploration de la pente » vous aidera à mieux comprendre la pente d'une ligne. (Du papier millimétré peut être utilisé à la place d'un géoboard, si nécessaire.)

Nous allons commencer par étirer un élastique entre deux piquets, comme indiqué sur la figure$\PageIndex{1}$.

La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 4 et la cheville de la colonne 4, rangée 2, formant une ligne. — Figurine$\PageIndex{1}$

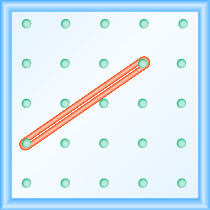
Ça ne ressemble pas à une ligne ?

Nous étendons maintenant une partie de l'élastique directement vers le haut à partir de la cheville gauche et autour d'une troisième cheville pour former les côtés d'un triangle droit, comme indiqué sur la figure$\PageIndex{2}$

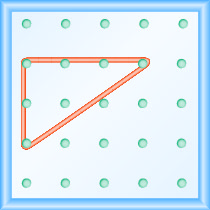
Nous faisons soigneusement un angle de 90° autour de la troisième cheville, de sorte que l'une des lignes nouvellement formées soit verticale et l'autre horizontale.

Pour déterminer la pente de la ligne, nous mesurons la distance le long des côtés verticaux et horizontaux du triangle. La distance verticale est appelée montée et la distance horizontale est appelée course, comme le montre la figure$\PageIndex{3}$.

Dans cette illustration, il y a deux lignes perpendiculaires avec des flèches. La première ligne s'étend tout droit vers le haut et est étiquetée « montée ». La deuxième flèche s'étend tout droit vers la droite et s'intitule « Exécuter ». — Figurine$\PageIndex{3}$

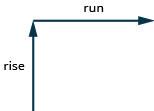
Si notre géoboard et notre élastique ressemblent à ceux de la figure$\PageIndex{4}$, la hausse est de 2. L'élastique monte de 2 unités. (Chaque espace est une unité.)

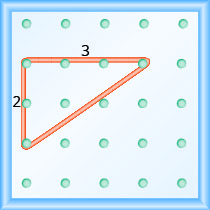
La hausse sur ce géoboard est de 2, car l'élastique augmente de deux unités.

Qu'est-ce que la course ?

L'élastique est réparti sur 3 unités. La course est de 3 (voir Figure$\PageIndex{4}$).

La pente d'une ligne est le rapport entre la montée et la course. En mathématiques, il est toujours désigné par la lettre m.

PENTE D'UNE LIGNE

La pente d'une ligne d'une ligne est$m = \frac{\text{rise}}{\text{run}}$.

La hausse mesure la variation verticale et la course mesure la variation horizontale entre deux points de la ligne.

Quelle est la pente de la ligne sur le géoboard de la figure$\PageIndex{4}$ ?

\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]

La ligne est inclinée$\frac{2}{3}$. Cela signifie que la ligne augmente de 2 unités pour 3 unités de course.

Lorsque nous travaillons avec des géoboards, il est conseillé de prendre l'habitude de commencer par un point d'ancrage situé à gauche et de le connecter à un point d'ancrage situé à droite. Si la hausse augmente, elle est positive et si elle diminue, elle est négative. La course se déroulera de gauche à droite et sera positive.

Exercice$\PageIndex{1}$

Quelle est la pente de la ligne sur le géoboard affiché ?

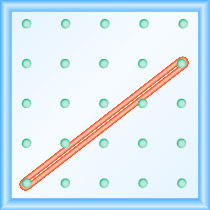
$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 5 et la cheville de la colonne 5, rangée 2, formant une ligne.$

Réponse

Utilisez la définition de pente :$m = \frac{\text{rise}}{\text{run}}$.

Commencez par le piquet gauche et comptez les espaces vers le haut et vers la droite pour atteindre le deuxième piquet.

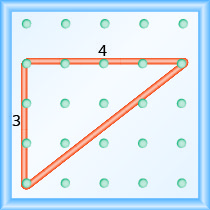
$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 2, la cheville de la colonne 1, rangée 5 et la cheville de la colonne 5, rangée 2, formant un triangle droit. La cheville 1, 2 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 1, 5 à la cheville 5, 2 forme l'hypoténuse du triangle. La ligne allant de la cheville 1, 2 à la broche 1, 5 est étiquetée « 3 ». La ligne allant de la broche 1, 2 à la broche 5, 2 est étiquetée « 4 ».$

\[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]

Cela signifie que la ligne augmente de 3 unités pour 4 unités de course.

Exercice$\PageIndex{2}$

Quelle est la pente de la ligne sur le géoboard affiché ?

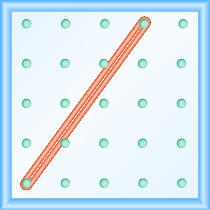
Réponse: $\frac{4}{3}$

Exercice$\PageIndex{3}$

Quelle est la pente de la ligne sur le géoboard affiché ?

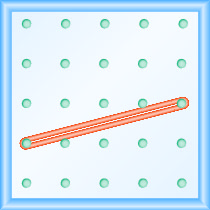
$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 4 et la cheville de la colonne 5, rangée 3, formant une ligne.$

Réponse: $\frac{1}{4}$

Exercice$\PageIndex{4}$

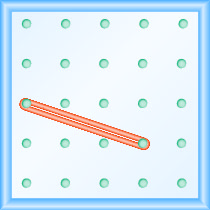
Quelle est la pente de la ligne sur le géoboard affiché ?

$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 3 et la cheville de la colonne 4, rangée 4, formant une ligne.$

Réponse

Utilisez la définition de pente :$m = \frac{\text{rise}}{\text{run}}$.

Commencez par le piquet de gauche et comptez les unités vers le bas et vers la droite pour atteindre le second pion.

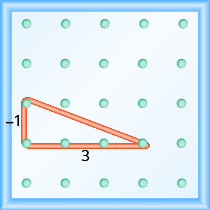
$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 3, la cheville de la colonne 1, rangée 4 et la cheville de la colonne 4, rangée 4, formant un triangle droit. La cheville 1, 3 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 1, 4 à la cheville 4, 4 forme l'hypoténuse du triangle. La ligne allant de la cheville 1, 3 à la borne 1, 4 est étiquetée « négatif 1 ». La ligne allant de la cheville 1, 4 à la broche 4, 4 est étiquetée « 3 ».$

\[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]

Cela signifie que la ligne baisse d'une unité pour 3 unités de course.

Exercice$\PageIndex{5}$

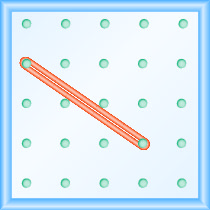
Quelle est la pente de la ligne sur le géoboard ?

$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 2 et la cheville de la colonne 4, rangée 4, formant une ligne.$

Réponse: $-\frac{2}{3}$

Exercice$\PageIndex{6}$

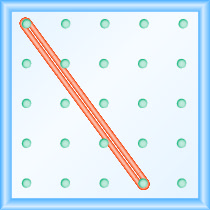
Quelle est la pente de la ligne sur le géoboard ?

$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 1 et la cheville de la colonne 4, rangée 5, pour former une ligne.$

Réponse: $-\frac{4}{3}$

Notez que dans l'exercice,$\PageIndex{1}$ la pente est positive et que dans l'exercice,$\PageIndex{4}$ la pente est négative. Avez-vous remarqué une différence entre les deux lignes de la Figure (a) et de la Figure (b) ?

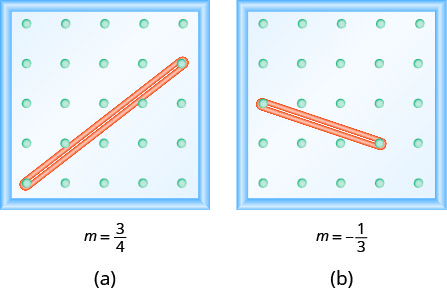
La figure montre deux grilles de piquets régulièrement espacés, l'un étiqueté (a) et l'autre étiqueté (b). Il y a 5 colonnes et 5 rangées de piquets dans chaque grille. Dans la grille (a), un élastique est tendu entre la cheville de la colonne 1, rangée 5 et la cheville de la colonne 5, rangée 2, formant une ligne. En dessous de cette grille se trouve la pente d'une droite définie comme m égale aux 3 quarts. Dans la grille (b), un élastique est tendu entre la cheville de la colonne 1, rangée 3 et la cheville de la colonne 4, rangée 4, formant une ligne. En dessous de cette grille se trouve la pente d'une droite définie comme m égale moins un tiers. — Figurine$\PageIndex{5}$

Nous « lisons » une ligne de gauche à droite comme nous lisons des mots en anglais. Comme vous pouvez le lire de gauche à droite, la ligne de la figure (a) monte ; elle a une pente positive. La ligne de la figure (b) descend ; elle présente une pente négative.

PENTES POSITIVES ET NÉGATIVES

La figure montre deux lignes côte à côte. La ligne de gauche est une ligne diagonale qui s'élève de gauche à droite. Il est étiqueté « Pente positive ». La ligne de droite est une ligne diagonale qui descend de gauche à droite. Il est étiqueté « Pente négative ». — Figurine$\PageIndex{6}$

Exercice$\PageIndex{7}$

Utilisez un géoboard pour modéliser une ligne avec une pente$\frac{1}{2}$.

Réponse

Pour modéliser une ligne sur un géoboard, nous avons besoin de la montée et de la course.

$\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}$

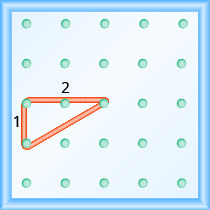
$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 3, la cheville de la colonne 1, rangée 4 et la cheville de la colonne 3, rangée 3, formant un triangle droit. La cheville 1, 3 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 1, 4 à la cheville 3, 3 forme l'hypoténuse du triangle. La ligne allant de la cheville 1, 3 à la broche 1, 4 est étiquetée « 1 ». La ligne allant de la cheville 1, 3 à la broche 3, 3 est étiquetée « 2 ».$

L'hypoténuse du triangle droit formé par l'élastique représente une ligne dont la pente est$\frac{1}{2}$.

Exercice$\PageIndex{8}$

Modélisez la pente$m = \frac{1}{3}$. Dessinez une image pour montrer vos résultats.

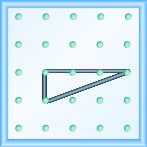
Réponse: $La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 2, rangée 3, la cheville de la colonne 2, rangée 4 et la cheville de la colonne 5, rangée 3, formant un triangle droit. La cheville 2, 3 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 2, 4 à la cheville 5, 3 constitue l'hypoténuse du triangle.$

Exercice$\PageIndex{9}$

Modélisez la pente$m = \frac{3}{2}$. Dessinez une image pour montrer vos résultats.

Réponse: $La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 1, la cheville de la colonne 1, rangée 4 et la cheville de la colonne 3, rangée 1, formant un triangle droit. La cheville 1, 1 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 1, 4 à la cheville 3, 1 forme l'hypoténuse du triangle.$

Exercice$\PageIndex{10}$

Utilisez un géoboard pour modéliser une ligne avec une pente$\frac{-1}{4}$.

Réponse

$\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}$

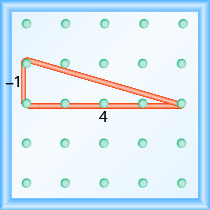
$La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 2, la cheville de la colonne 1, rangée 3 et la cheville de la colonne 5, rangée 3, formant un triangle droit. La cheville 1, 3 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 1, 2 à la cheville 5, 3 forme l'hypoténuse du triangle. La ligne allant de la cheville 1, 2 à la borne 1, 3 est étiquetée « négatif 1 ». La ligne allant de la broche 1, 3 à la broche 5, 3 est étiquetée « 4 ».$

L'hypoténuse du triangle droit formé par l'élastique représente une ligne dont la pente est$\frac{-1}{4}$.

Exercice$\PageIndex{11}$

Modélisez la pente$m = \frac{-2}{3}$. Dessinez une image pour montrer vos résultats.

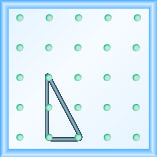
Réponse: $La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 2, rangée 3, la cheville de la colonne 2, rangée 5 et la cheville de la colonne 3, rangée 5, formant un triangle droit. La cheville 2, 5 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 2, 3 à la cheville 3, 5 forme l'hypoténuse du triangle.$

Exercice$\PageIndex{12}$

Modélisez la pente$m = \frac{-1}{3}$. Dessinez une image pour montrer vos résultats.

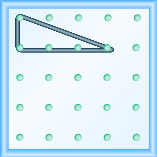
Réponse: $La figure montre une grille de piquets régulièrement espacés. Il y a 5 colonnes et 5 rangées de piquets. Un élastique est tendu entre la cheville de la colonne 1, rangée 1, la cheville de la colonne 1, rangée 2 et la cheville de la colonne 4, rangée 2, formant un triangle droit. La cheville 1, 2 forme le sommet de l'angle de 90 degrés et la ligne allant de la cheville 1, 1 à la cheville 4, 2 forme l'hypoténuse du triangle.$

$m = \frac{\text{rise}}{\text{run}}$À utiliser pour déterminer la pente d'une droite à partir de son graphe

Nous allons maintenant examiner certains graphiques sur le plan de coordonnées xy et voir comment déterminer leurs pentes. La méthode sera très similaire à celle que nous venons de modéliser sur nos géoboards.

Pour trouver la pente, il faut compter la montée et la course. Mais par où commencer ?

Nous localisons deux points sur la ligne dont les coordonnées sont des nombres entiers. Nous commençons ensuite par le point situé à gauche et dessinons un triangle droit, afin de pouvoir compter les montées et les descentes.

Exercice$\PageIndex{13}$:

Détermine la pente de la ligne affichée.

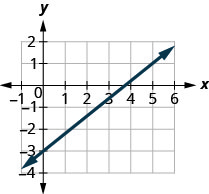
$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 6 et l'axe y va de moins 4 à 2. Une ligne passe par les points (0, moins 3) et (5, 1).$

Réponse: $Ce tableau comporte trois colonnes et quatre lignes. La première rangée indique : « Étape 1. Localisez deux points sur le graphique dont les coordonnées sont des nombres entiers. Note (0, moins 3) et (5, 1). » À droite se trouve une ligne tracée sur le plan de coordonnées x. L'axe X du plan va de moins 1 à 6. L'axe Y du plan va de moins 4 à 2. Les points (0, moins 3) et (5, 1) sont tracés.$ $La deuxième rangée indique : « Étape 2. En commençant par le point de gauche, esquissez un triangle droit en allant du premier point au deuxième point. À partir de (0, moins 3), esquissez un triangle droit jusqu'à (5, 1). » Dans le graphique de droite, un point supplémentaire est tracé en (0, 1). Les trois points forment un triangle droit, la droite allant de (0, moins 3) à (5, 1) formant l'hypoténuse et les droites allant de (0, moins 3) à (0, 1) et (0, 1) à (5, 1) formant les jambes.$ $La troisième rangée indique alors : « Étape 3. Comptez la montée et la course sur les jambes du triangle. » La hausse est de 4 et la course de 5.$ $La quatrième rangée indique : « Étape 4. Prenez le rapport entre la montée et la course pour trouver la pente. Utilisez la formule de pente. Remplacez les valeurs de la hausse et de la course. » À droite se trouve la formule de pente, m est égal à la hausse divisée par la course. La pente de la ligne est de 4 divisée par 5, soit quatre cinquièmes. Cela signifie que y augmente de 4 unités alors que x augmente de 5 unités.$

Exercice$\PageIndex{14}$

Détermine la pente de la ligne affichée.

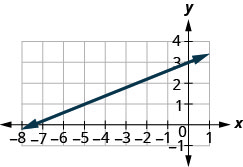
$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 8 à 1 et l'axe y va de moins 1 à 4. Une ligne passe par les points (moins 5, 1) et (0, 3).$

Réponse: $\frac{2}{5}$

Exercice$\PageIndex{15}$

Détermine la pente de la ligne affichée.

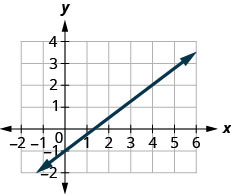
$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 5 et l'axe y va de moins 2 à 4. Une ligne passe par les points (0, moins 1) et (4, 2).$

Réponse: $\frac{3}{4}$

TROUVEZ LA PENTE D'UNE LIGNE À PARTIR DE SON GRAPHIQUE

Localisez deux points sur la ligne dont les coordonnées sont des nombres entiers.
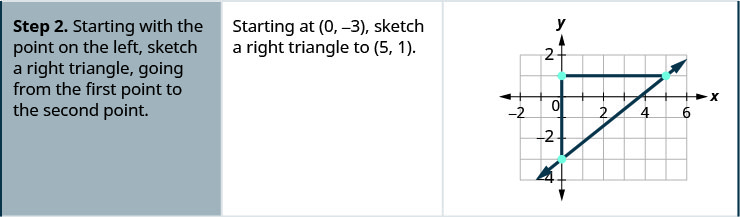
En commençant par le point de gauche, esquissez un triangle droit en allant du premier point au deuxième point.
Comptez la montée et la course sur les jambes du triangle.
Prenez le rapport entre la montée et la course pour trouver la pente,$m = \frac{\text{rise}}{\text{run}}$.

Exercice$\PageIndex{16}$

Détermine la pente de la ligne affichée.

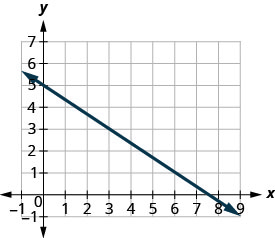
$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 9 et l'axe y va de moins 1 à 7. Une ligne passe par les points (0, 5), (3, 3) et (6, 1).$

Réponse

Localisez deux points sur le graphique dont les coordonnées sont des nombres entiers.	(0,5) et (3,3)
Quel point se trouve sur la gauche ?	(0,5)
À partir de (0,5), esquissez un triangle droit jusqu'à (3,3).	$.$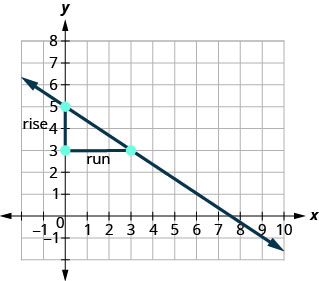
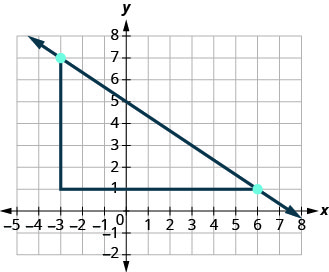
Comptez la hausse, elle est négative.	La hausse est de −2.
Comptez le nombre de courses.	La course est de 3.
Utilisez la formule de pente.	$m = \frac{\text{rise}}{\text{run}}$
Remplacez les valeurs de la hausse et de la course.	$m = \frac{-2}{3}$
Simplifiez.	$m = -\frac{2}{3}$
	La pente de la ligne est$-\frac{2}{3}$.

Donc y augmente de 3 unités lorsque xx diminue de 2 unités.

Et si nous utilisions les points (−3,7) et (6,1) pour déterminer la pente de la droite ?

$Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 7 à 7. Une ligne passe par les points (moins 3, 7) et (6, 1). Un point supplémentaire est tracé à (négatif 3, 1). Les trois points forment un triangle droit, la ligne allant de (négatif 3, 7) à (6, 1) formant l'hypoténuse et les lignes allant de (négatif 3, 7) à moins 1, 7) et de (négatif 1, 7) à (6, 1) formant les jambes.$

La hausse serait de −6 et la course serait de 9. Ensuite$m = \frac{-6}{9}$, et cela simplifie$m = -\frac{2}{3}$. N'oubliez pas que peu importe les points que vous utilisez, la pente de la ligne est toujours la même.

Exercice$\PageIndex{17}$

Détermine la pente de la ligne affichée.

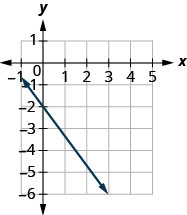
$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 5 et l'axe y va de moins 6 à 1. Une ligne passe par les points (0, moins 2) et (3, moins 6).$

Réponse: $-\frac{4}{3}$

Exercice$\PageIndex{18}$

Détermine la pente de la ligne affichée.

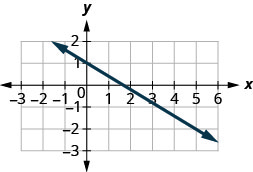
$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 3 à 6 et l'axe y va de moins 3 à 2. Une ligne passe par les points (0, 1) et (5, moins 2).$

Réponse: $-\frac{3}{5}$

Dans les deux derniers exemples, les lignes comportaient des interceptions y avec des valeurs entières. Il était donc pratique d'utiliser l'intersection y comme l'un des points pour trouver la pente. Dans l'exemple suivant, l'intersection y est une fraction. Au lieu d'utiliser ce point, nous allons rechercher deux autres points dont les coordonnées sont des nombres entiers. Cela facilitera les calculs de pente.

Exercice$\PageIndex{19}$

Détermine la pente de la ligne affichée.

$Le graphique montre le plan de coordonnées x y. L'axe X va de 0 à 8 et l'axe y va de 0 à 7. Une ligne passe par les points (2, 3) et (7, 6).$

Réponse

Localisez deux points sur le graphique dont les coordonnées sont des nombres entiers.	(2,3) et (7,6)
Quel point se trouve sur la gauche ?	(2,3)
À partir de (2,3), esquissez un triangle droit jusqu'à (7,6).	$.$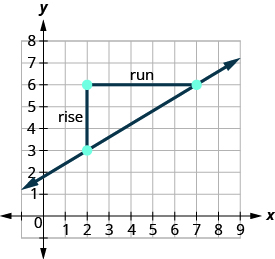
Comptez la hausse.	La hausse est de 3.
Comptez le nombre de courses.	La course est de 5.
Utilisez la formule de pente.	$m = \frac{\text{rise}}{\text{run}}$
Remplacez les valeurs de la hausse et de la course.	$m = \frac{3}{5}$
	La pente de la ligne est$\frac{3}{5}$.

Cela signifie que y augmente de 5 unités alors que x augmente de 3 unités.

Lorsque nous avons utilisé des géoboards pour introduire le concept de pente, nous avons dit que nous allions toujours commencer par le point situé à gauche et compter la montée et la course pour arriver au point situé à droite. Ainsi, la course était toujours positive et la montée déterminait si la pente était positive ou négative.

Que se passerait-il si nous commencions par le point sur la droite ?

Utilisons à nouveau les points (2,3) et (7,6), mais nous allons maintenant commencer à (7,6).

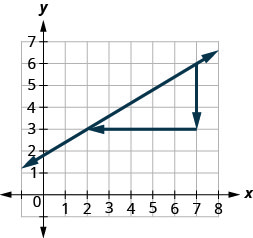
$Le graphique montre le plan de coordonnées x y. L'axe X s'étend de 0 à 8. L'axe y va de 0 à 7. Une ligne passe par les points (2, 3) et (7, 6). Un point supplémentaire est tracé en (7, 3). Les trois points forment un triangle droit, la ligne de (2, 3) à (7, 6) formant l'hypoténuse et les lignes de (2, 3) à (7, 3) et de (7, 3) à (7, 6) formant les jambes.$

$\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}$

Peu importe où vous commencez, la pente de la ligne est toujours la même.

Exercice$\PageIndex{20}$

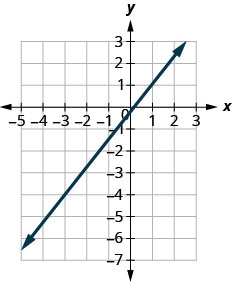
Détermine la pente de la ligne affichée.

$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 4 à 2 et l'axe y va de moins 6 à 2. Une ligne passe par les points (moins 3, 4) et (1, 1).$

Réponse: $\frac{5}{4}$

Exercice$\PageIndex{21}$

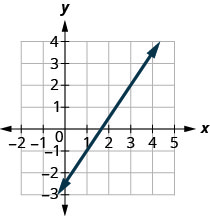
Détermine la pente de la ligne affichée.

$Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 4 et l'axe y va de moins 2 à 3. Une ligne passe par les points (1, moins 1) et (3, 2).$

Réponse: $\frac{3}{2}$

Déterminer la pente des lignes horizontales et verticales

Vous souvenez-vous de la particularité des lignes horizontales et verticales ? Leurs équations ne comportaient qu'une seule variable.

\[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]

Alors, comment trouver la pente de la ligne horizontale y=4y=4 ? Une approche consisterait à tracer la ligne horizontale, à y trouver deux points et à compter la hausse et la course. Voyons ce qui se passe lorsque nous faisons cela.

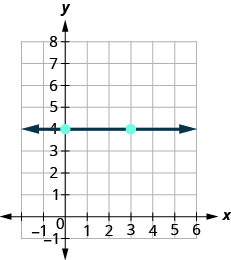
Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 5 et l'axe y va de moins 1 à 7. Une ligne passe par les points (0, 4) et (3, 4). — Figurine$\PageIndex{7}$

$\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}$

Toutes les lignes horizontales ont une pente 0. Lorsque les coordonnées y sont identiques, la hausse est de 0.

PENTE D'UNE LIGNE HORIZONTALE

La pente d'une ligne horizontale, y=b, est de 0.

Le sol de votre pièce est horizontal. Sa pente est de 0. Si vous placez soigneusement une balle sur le sol, elle ne roulera pas.

Maintenant, nous allons considérer une ligne verticale, la ligne.

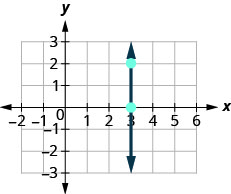
Le graphique montre le plan de coordonnées x y. L'axe X va de moins 1 à 5 et l'axe y va de moins 2 à 2. Une ligne passe par les points (3, 0) et (3, 2). — Figurine$\PageIndex{8}$

$\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}$

Mais on ne peut pas diviser par 0. La division par 0 n'est pas définie. Nous disons donc que la pente de la ligne verticale x=3x=3 n'est pas définie.

La pente d'une ligne verticale n'est pas définie. Lorsque les coordonnées x d'une ligne sont toutes identiques, l'intervalle est égal à 0.

PENTE D'UNE LIGNE VERTICALE

La pente d'une ligne verticale, x=a, n'est pas définie.

Exercice$\PageIndex{22}$

Déterminez la pente de chaque ligne :

ⓐ x=8 ⓑ y=−5.

Réponse: ⓐ x=8
Il s'agit d'une ligne verticale.
Sa pente n'est pas définie.

ⓑ y=−5
Il s'agit d'une ligne horizontale.
Il a une pente 0.

Exercice$\PageIndex{23}$

Détermine la pente de la droite : x=−4.

Réponse: indéfini

Exercice$\PageIndex{24}$

Détermine la pente de la droite : y=7.

Réponse: 0

GUIDE RAPIDE DES PENTES DES LIGNES

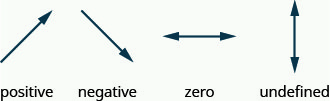
Cette figure montre quatre lignes avec des flèches. La première ligne s'élève et se dirige vers la droite. Il a une pente positive. La deuxième ligne tombe et se dirige vers la droite. Il a une pente négative. La troisième ligne n'est ni ascendante ni descendante, s'étendant horizontalement dans les deux sens. Sa pente est nulle. La quatrième ligne est complètement verticale, une extrémité s'élevant vers le haut et l'autre vers le bas, ne pointant ni vers la gauche ni vers la droite. Sa pente n'est pas définie. — Figurine$\PageIndex{9}$

N'oubliez pas que nous « lisons » une ligne de gauche à droite, tout comme nous lisons des mots écrits en anglais.

Utilisez la formule de pente pour déterminer la pente d'une droite entre deux points

L'activité de mathématiques manipulatrices « Pente des lignes entre deux points » vous aidera à mieux comprendre comment déterminer la pente d'une droite entre deux points.

Parfois, nous aurons besoin de déterminer la pente d'une droite entre deux points alors que nous n'avons pas de graphique pour compter la hausse et la course. Nous pourrions tracer les points sur du papier quadrillé, puis compter la montée et la course, mais comme nous le verrons, il existe un moyen de trouver la pente sans représenter graphiquement. Avant d'y aller, nous devons introduire une notation algébrique.

Nous avons vu qu'une paire ordonnée (x, y) donne les coordonnées d'un point. Mais lorsque nous travaillons avec des pentes, nous utilisons deux points. Comment utiliser le même symbole (x, y) pour représenter deux points différents ? Les mathématiciens utilisent des indices pour distinguer les points.

\[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]

L'utilisation d'indices en mathématiques ressemble beaucoup à l'utilisation des initiales du nom de famille à l'école primaire. Peut-être vous souvenez-vous de Laura C. et Laura M. dans votre classe de troisième année ?

Nous utiliserons$\left(x_{1}, y_{1}\right)$ pour identifier le premier point et$\left(x_{2}, y_{2}\right)$ pour identifier le second point.

Si nous avions plus de deux points, nous pourrions utiliser$\left(x_{3}, y_{3}\right)$$\left(x_{4}, y_{4}\right)$, et ainsi de suite.

Voyons comment la montée et la course sont liées aux coordonnées des deux points en examinant à nouveau la pente de la ligne entre les points (2,3) et (7,6).

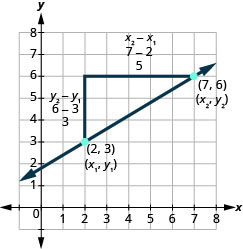
Le graphique montre le plan de coordonnées x y. Les axes x et y vont de 0 à 7. Une ligne passe par les points (2, 3) et (7, 6), qui sont tracés et étiquetés. La paire ordonnée (2, 3) est étiquetée (indice x 1, indice y 1). La paire ordonnée (7, 6) est étiquetée (indice x 2, indice y 2). Un point supplémentaire est tracé en (2, 6). Les trois points forment un triangle droit, la ligne de (2, 3) à (7, 6) formant l'hypoténuse et les lignes de (2, 3) à (2, 6) et de (2, 6) à (7, 6) formant les jambes. La première étape, de (2, 3) à (2, 6) est étiquetée par l'indice 2 moins y indice 1, 6 moins 3 et 3. La deuxième étape, de (2, 3) à (7, 6), est étiquetée x indice 2 moins x indice 1, y moins 2 et 5. — Figurine$\PageIndex{10}$

Comme nous avons deux points, nous utiliserons la notation en indice,$\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)$.

Sur le graphique, nous avons compté la hausse de 3 et la course de 5.

Notez que la hausse de 3 peut être trouvée en soustrayant les coordonnées y 6 et 3.

\[3=6-3\]

Et l'intervalle de 5 peut être trouvé en soustrayant les coordonnées x 7 et 2.

\[5 = 7 - 2\]

Nous le savons$m = \frac{\text{rise}}{\text{run}}$. Donc$m = \frac{3}{5}$.

Nous réécrivons la montée et la course en saisissant les coordonnées$m = \frac{6-3}{7-2}$

Mais 6 est y2, la coordonnée y du deuxième point et 3 est y1, la coordonnée y du premier point.

Nous pouvons donc réécrire la pente en utilisant la notation en indice. $m = \frac{y2-y1}{7-2}$

De même, 7 est x2, la coordonnée x du deuxième point et 2 est x1, la coordonnée x du premier point.

Donc, encore une fois, nous réécrivons la pente en utilisant la notation en indice. $m = \frac{y2-y1}{x2-x1}$

Nous avons montré qu'il$m = \frac{y2-y1}{x2-x1}$ s'agit vraiment d'une autre version de$m = \frac{\text{rise}}{\text{run}}$. Nous pouvons utiliser cette formule pour déterminer la pente d'une droite lorsque nous avons deux points sur la ligne.

FORMULE SLOPE

La pente de la ligne entre deux points$\left(x_{1}, y_{1}\right)$ et$\left(x_{2}, y_{2}\right)$ est

\[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]

Il s'agit de la formule de pente.

La pente est la suivante :

\[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]

Exercice$\PageIndex{25}$

Utilisez la formule de pente pour déterminer la pente de la droite entre les points (1,2) et (4,5).

Réponse

$\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}$

Confirmons cela en comptant la pente sur un graphique en utilisant$m = \frac{\text{rise}}{\text{run}}$.

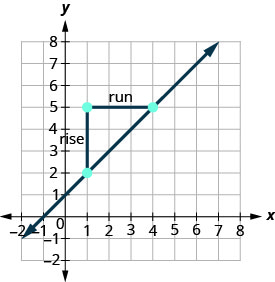
$Le graphique montre le plan de coordonnées x y. Les axes x et y du plan vont de 0 à 7. Une ligne passe par les points (1, 2) et (4, 5) qui sont tracés. Un point supplémentaire est tracé en (1, 5). Les trois points forment un triangle droit, la ligne de (1, 2) à (4, 5) formant l'hypoténuse et les lignes de (1, 2) à (1, 5) et de (1, 5) à (4, 5) formant les jambes. La jambe de (1, 2) à (1, 5) est étiquetée « monter » et la jambe de (1, 5) à (4, 5) est étiquetée « courir ».$

Peu importe le point que vous appelez le point #1 et celui que vous appelez le point #2. La pente sera la même. Essayez le calcul vous-même.

Exercice$\PageIndex{26}$

Utilisez la formule de pente pour déterminer la pente de la ligne passant par les points : (8,5) et (6,3).

Réponse: 1

Exercice$\PageIndex{27}$

Utilisez la formule de pente pour déterminer la pente de la ligne passant par les points : (1,5) et (5,9).

Réponse: 1

Exercice$\PageIndex{28}$

Utilisez la formule de pente pour déterminer la pente de la droite passant par les points (−2, −3) et (−7,4).

Réponse

$\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}$

Vérifions cette pente sur le graphique présenté.

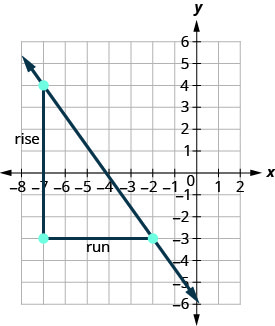
$Le graphique montre le plan de coordonnées x y. L'axe X du plan va de moins 8 à 2 et l'axe y du plan va de moins 6 à 5. Une ligne passe par les points (négatif 7, 4) et (négatif 2, négatif 3), qui sont tracés et étiquetés. Un point supplémentaire est tracé à (négatif 7, négatif 3). Les trois points forment un triangle droit, la droite allant de (négatif 7, 4) à (négatif 2, négatif 3) formant l'hypoténuse et les droites de (négatif 7, 4) à (négatif 7, moins 3) et de (négatif 7, négatif 3) à (négatif 2, négatif 3) formant les jambes. La jambe de (négatif 7, 4) à (négatif 7, négatif 3) est étiquetée « montée » et la jambe de (négatif 7, négatif 3) à (négatif 2, négatif 3) est étiquetée « courir ».$

\[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]

Exercice$\PageIndex{29}$

Utilisez la formule de pente pour déterminer la pente de la droite passant par les points : (−3,4) et (2, −1).

Réponse: -1

Exercice$\PageIndex{30}$

Utilisez la formule de pente pour déterminer la pente de la droite passant par la paire de points : (−2,6) et (−3, −4).

Réponse: 10

Tracez une droite en fonction d'un point et de la pente

Jusqu'à présent, dans ce chapitre, nous avons tracé des lignes en traçant des points, en utilisant des interceptions et en reconnaissant des lignes horizontales et verticales.

Une autre méthode que nous pouvons utiliser pour tracer des lignes est la méthode point—pente. Nous utiliserons cette méthode lorsque nous connaîtrons un point et la pente de la ligne. Nous allons commencer par tracer le point, puis utiliser la définition de la pente pour dessiner le graphique de la droite.

Exercice$\PageIndex{31}$

Tracez la droite passant par le point (1, -1) dont la pente est$m = \frac{3}{4}$.

Réponse: $Ce tableau comporte trois colonnes et quatre lignes. La première rangée indique : « Étape 1. Tracez le point donné. Diagramme (1, négatif 1). » À droite se trouve un graphique du plan de coordonnées x. L'axe X du plan va de moins 1 à 7. L'axe Y du plan va de moins 3 à 4. Le point (0, moins 1) est tracé.$ $La deuxième rangée indique : « Étape 2. Utilisez la formule de pente m égale la montée divisée par la course pour identifier la montée et la course. » Les valeurs de montée et de descente sont de 3 et 4, donc m est égal à 3 divisé par 4.$ $La troisième rangée indique « Étape 3. À partir du point donné, comptez la montée et la course pour marquer le deuxième point. » Nous commençons à (1, moins 1) et comptons la hausse et la course. Trois unités vers le haut et 4 unités vers la droite. Dans le graphique de droite, deux points supplémentaires sont tracés : (1, 2), soit 3 unités au-dessus de (1, moins 1), et (5, 2), qui se trouve à 3 unités en haut et 4 unités à droite de (1, moins 1).$ $La quatrième rangée indique « Étape 4. Reliez les points par une ligne. » Sur le graphique de droite, une ligne est tracée entre les points (1, moins 1) et (5, 2). Cette droite est également l'hypoténuse du triangle droit formé par les trois points (1, négatif 1), (1, 2) et (5, 2).$

Exercice$\PageIndex{32}$

Tracez la droite passant par le point (2, −2) avec la pente$m = \frac{4}{3}$.

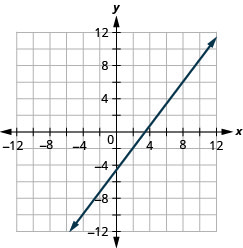
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 12 à 12. Une ligne passe par les points (moins 4, moins 10) et (2, moins 2).$

Exercice$\PageIndex{33}$

Tracez la droite passant par le point (−2,3) avec la pente$m=\frac{1}{4}$.

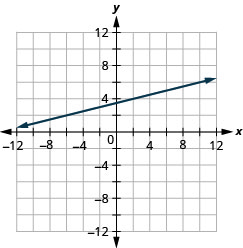
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 12 à 12. Une ligne passe par les points (moins 2, 3) et (10, 6).$

TRACEZ UNE LIGNE EN FONCTION D'UN POINT ET DE LA PENTE.

Tracez le point donné.
Utilisez la formule$m=\frac{\text { rise }}{\text { rise }}$ de pente pour identifier la montée et la course.
À partir du point donné, comptez la montée et la course pour marquer le deuxième point.
Reliez les points par une ligne.

Exercice$\PageIndex{34}$

Tracez la droite avec y -intercept 2 dont la pente est$m=−\frac{2}{3}$.

Réponse

Tracez le point donné, l'intersection y, (0,2).

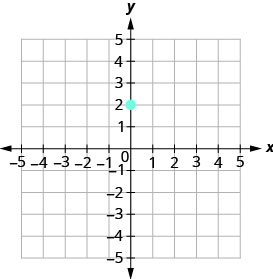
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 5 à 5. Le point (0, 2) est tracé.$

$\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}$

Comptez la montée et la course. Marquez le deuxième point.

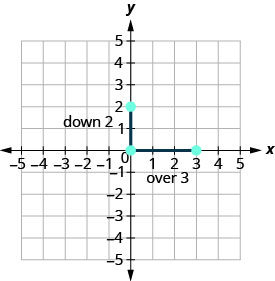
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 5 à 5. Les points (0, 2), (0, 0) et (3,0) sont tracés et étiquetés. La ligne de (0, 2) à (0, 0) est étiquetée « down 2 » et la ligne de (0, 0) à (3, 0) est étiquetée « right 3 ».$

Reliez les deux points par une ligne.

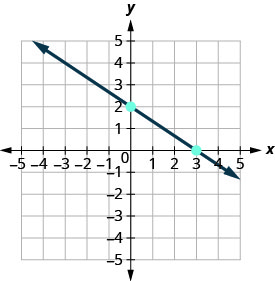
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 5 à 5. Une ligne passe par les points tracés (0, 2) et (3,0).$

Vous pouvez vérifier votre travail en trouvant un troisième point. Puisque la pente est$m=−\frac{2}{3}$, elle peut être écrite comme$m=\frac{2}{-3}$. Revenez à (0,2) et comptez la hausse, 2, et la course, −3.

Exercice$\PageIndex{35}$

Tracez la droite avec l'intersection y 4 et la pente$m=−\frac{5}{2}$.

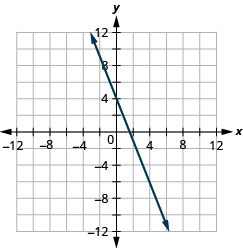
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 12 à 12. Une ligne intercepte l'axe y en (0, 4) et passe par le point (4, moins 6).$

Exercice$\PageIndex{36}$

Tracez la droite avec l'intersection x −3 et la pente$m=−\frac{3}{4}$.

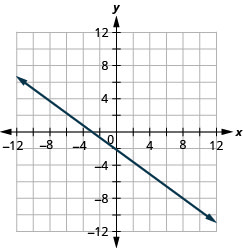
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 12 à 12. Une ligne intercepte l'axe X en (moins 3, 0) et passe par le point (1, moins 3).$

Exercice$\PageIndex{37}$

Tracez la droite passant par le point (-1, -3) dont la pente est m=4.

Réponse

Tracez le point donné.

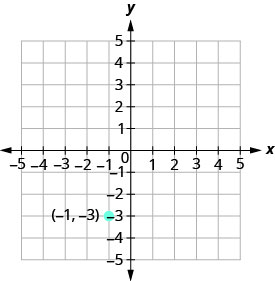
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 5 à 5. Le point (négatif 1, négatif 3) est tracé et étiqueté.$

$\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}$

Comptez la montée et la course et marquez le deuxième point.

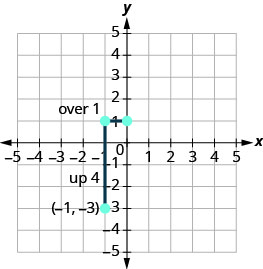
$Cette figure montre comment tracer la droite passant par le point (négatif 1, moins 3) dont la pente est de 4. La première étape consiste à identifier la hausse et la course. La montée est de 4 et la course est de 1. 4 divisée par 1 est 4, donc la pente est de 4. Ensuite, nous comptons la montée et la course et marquons le deuxième point. À droite se trouve un graphique du plan de coordonnées x. Les axes x et y vont de moins 5 à 5. Nous commençons par le point tracé (négatif 1, négatif 3) et comptons la hausse, 4. Nous atteignons le point négatif 1, 1, que nous tracons. Nous comptons ensuite la course à partir de ce point, qui est de 1. Nous atteignons le point (0, 1), qui est tracé. La dernière étape consiste à relier les deux points par une ligne. Nous tracons une ligne qui passe par les points (moins 1, moins 3) et (0, 1).$

Reliez les deux points par une ligne.

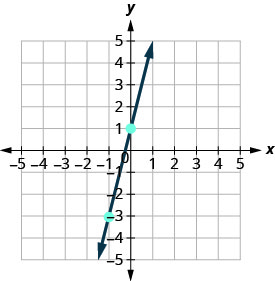
$Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 5 à 5. Une ligne passe par les points tracés (-1, -3) et (1,0).$

Vous pouvez vérifier votre travail en trouvant un troisième point. Comme la pente est m=4, elle peut être écrite sous la forme$m = \frac{-4}{-1}$. Revenez à (−1, −3) et comptez la hausse, −4, et la course, −1.

Exercice$\PageIndex{38}$

Tracez la droite avec le point (−2,1) et la pente m=3.

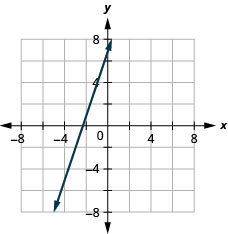
Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 7 à 7. Une ligne passe par les points (négatif 2, 1) et (négatif 1, 4).$

Exercice$\PageIndex{39}$

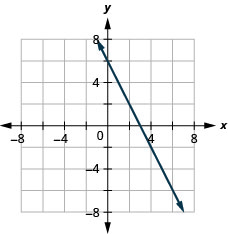
Tracez la droite avec le point (4, −2) et la pente m=−2.

Réponse: $Le graphique montre le plan de coordonnées x y. Les axes x et y vont de moins 7 à 7. Une ligne passe par les points (4, moins 2) et (5, moins 4).$

Résolvez les applications

Au début de cette section, nous avons indiqué qu'il existe de nombreuses applications de la pente dans le monde réel. Regardons-en quelques-unes maintenant.

Exercice$\PageIndex{40}$

La « pente » du toit d'un bâtiment est la pente du toit. Il est important de connaître le terrain dans les climats où il y a de fortes chutes de neige. Si le toit est trop plat, le poids de la neige peut provoquer son effondrement. Quelle est la pente du toit illustré ?

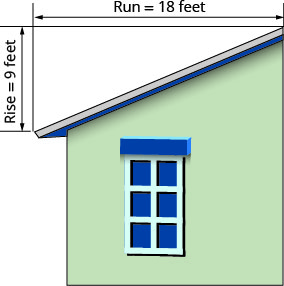
$Cette figure montre une maison avec un toit en pente. Le toit de la moitié du bâtiment est étiqueté « pente du toit ». Il y a un segment de ligne avec des flèches à chaque extrémité qui mesure la longueur verticale du toit et est étiqueté « la hauteur est égale à 9 pieds ». Il y a un segment de ligne avec des flèches à chaque extrémité qui mesurent la longueur horizontale de la racine et qui est étiqueté « courir est égal à 18 pieds ».$

Réponse: $\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}$

Exercice$\PageIndex{41}$

Utilisez Exercice$\PageIndex{40}$, en remplaçant la montée = 14 et la course = 24.

Réponse: $\frac{7}{12}$

Exercice$\PageIndex{42}$

Utilisez Exercice$\PageIndex{40}$, en remplaçant rise = 15 et course = 36.

Réponse: $\frac{5}{12}$

Exercice$\PageIndex{43}$

Avez-vous déjà pensé aux canalisations d'égout qui relient votre maison à la rue ? Ils doivent être inclinés$\frac{1}{4}$ pouce par pied afin de se drainer correctement. Quelle est la pente requise ?

$Cette figure est un triangle droit. Une jambe mesure moins un quart de pouce et l'autre un pied.$

Réponse

$\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}$

Le tuyau tombe de 1 pouce pour chaque 48 pouces de course horizontale.

Exercice$\PageIndex{44}$

Déterminez la pente d'un tuyau qui descend en$\frac{1}{3}$ pouces par pied.

Réponse: $-\frac{1}{36}$

Exercice$\PageIndex{45}$

Déterminez la pente d'un tuyau qui descend en$\frac{3}{4}$ pouces par mètre.

Réponse: $-\frac{1}{48}$

Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires sur la compréhension de la pente d'une ligne.

Concepts clés

Trouvez la pente d'une ligne à partir de son graphe en utilisant$m=\frac{\text { rise }}{\text { run }}$
1. Localisez deux points sur la ligne dont les coordonnées sont des nombres entiers.
2. En commençant par le point de gauche, esquissez un triangle droit en allant du premier point au deuxième point.
3. Comptez la montée et la course sur les jambes du triangle.
4. Prenez le rapport entre la montée et la course pour trouver la pente.
Tracez une droite en fonction d'un point et de la pente
1. Tracez le point donné.
2. Utilisez la formule$m=\frac{\text { rise }}{\text { run }}$ de pente pour identifier la montée et la course.
3. À partir du point donné, comptez la montée et la course pour marquer le deuxième point.
4. Reliez les points par une ligne.
Pente d'une ligne horizontale
- La pente d'une ligne horizontale, y=b, est de 0.
Pente d'une ligne verticale
- La pente d'une ligne verticale, x=a, n'est pas définie

Objectifs d'apprentissage

Remarque

Utiliser des géoboards pour modéliser la pente

PENTE D'UNE LIGNE

Exercice\(\PageIndex{1}\)

Exercice\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

Exercice\(\PageIndex{4}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

PENTES POSITIVES ET NÉGATIVES

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\)

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

\(m = \frac{\text{rise}}{\text{run}}\)À utiliser pour déterminer la pente d'une droite à partir de son graphe

Exercice\(\PageIndex{13}\):

Exercice\(\PageIndex{14}\)

Exercice\(\PageIndex{15}\)

TROUVEZ LA PENTE D'UNE LIGNE À PARTIR DE SON GRAPHIQUE

Exercice\(\PageIndex{16}\)

Exercice\(\PageIndex{17}\)

Exercice\(\PageIndex{18}\)

Exercice\(\PageIndex{19}\)

Exercice\(\PageIndex{20}\)

Exercice\(\PageIndex{21}\)

Déterminer la pente des lignes horizontales et verticales

PENTE D'UNE LIGNE HORIZONTALE

PENTE D'UNE LIGNE VERTICALE

Exercice\(\PageIndex{22}\)

Exercice\(\PageIndex{23}\)

Exercice\(\PageIndex{24}\)

GUIDE RAPIDE DES PENTES DES LIGNES

Utilisez la formule de pente pour déterminer la pente d'une droite entre deux points

FORMULE SLOPE

Exercice\(\PageIndex{25}\)

Exercice\(\PageIndex{26}\)

Exercice\(\PageIndex{27}\)

Exercice\(\PageIndex{28}\)

Exercice\(\PageIndex{29}\)

Exercice\(\PageIndex{30}\)

Tracez une droite en fonction d'un point et de la pente

Exercice\(\PageIndex{31}\)

Exercice\(\PageIndex{32}\)

Exercice\(\PageIndex{33}\)

TRACEZ UNE LIGNE EN FONCTION D'UN POINT ET DE LA PENTE.

Exercice\(\PageIndex{34}\)

Exercice\(\PageIndex{35}\)

Exercice\(\PageIndex{36}\)

Exercice\(\PageIndex{37}\)

Exercice\(\PageIndex{38}\)

Exercice\(\PageIndex{39}\)

Résolvez les applications

Exercice\(\PageIndex{40}\)

Exercice\(\PageIndex{41}\)

Exercice\(\PageIndex{42}\)

Exercice\(\PageIndex{43}\)

Exercice\(\PageIndex{44}\)

Exercice\(\PageIndex{45}\)

Concepts clés