4.1 : Utiliser le système de coordonnées rectangulaires
- Page ID
- 194756
À la fin de cette section, vous serez en mesure de :
- Tracer des points dans un système de coordonnées rectangulaires
- Vérifier les solutions à une équation à deux variables
- Compléter un tableau des solutions à une équation linéaire
- Trouvez des solutions à une équation linéaire à deux variables
Avant de commencer, répondez à ce questionnaire de préparation.
- Évaluez\(x+3\) quand\(x=−1\).
Si vous avez oublié ce problème, passez en revue l'exercice 1.5.25. - Evaluez\(2x−5y\) quand\(x=3\) et y=−2.
Si vous avez oublié ce problème, passez en revue l'exercice 1.5.28. - Résolu pour y :\(40−4y=20\)
Si vous avez oublié ce problème, passez en revue l'exercice 2.3.1.
Tracer des points sur un système de coordonnées rectangulaires
Tout comme les cartes utilisent un système de grille pour identifier les emplacements, un système de grille est utilisé en algèbre pour montrer une relation entre deux variables dans un système de coordonnées rectangulaires. Le système de coordonnées rectangulaires est également appelé plan xy ou « plan de coordonnées ».
La ligne numérique horizontale est appelée axe X. La ligne numérique verticale est appelée axe y. L'axe x et l'axe y forment ensemble le système de coordonnées rectangulaires. Ces axes divisent un plan en quatre régions, appelées quadrants. Les quadrants sont identifiés par des chiffres romains, en commençant en haut à droite et en continuant dans le sens antihoraire. Voir la figure\(\PageIndex{1}\).
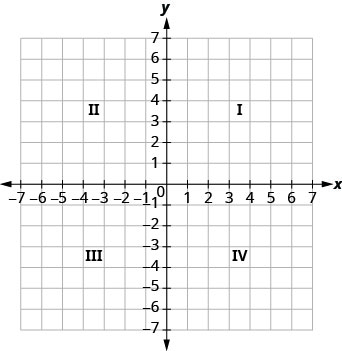
Dans le système de coordonnées rectangulaires, chaque point est représenté par une paire ordonnée. Le premier nombre de la paire ordonnée est la coordonnée x du point et le second est la coordonnée y du point.
Une paire ordonnée, (x, y) (x, y), donne les coordonnées d'un point dans un système de coordonnées rectangulaires.
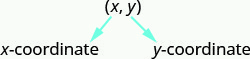
Le premier nombre est la coordonnée X.
Le deuxième nombre est la coordonnée y.
L'expression « paire commandée » signifie que la commande est importante. Quelle est la paire ordonnée du point où les axes se croisent ? À ce stade, les deux coordonnées sont nulles, donc leur paire ordonnée l'est\((0,0)\). Le point\((0,0)\) porte un nom spécial. C'est ce qu'on appelle l'origine.
Le point\((0,0)\) s'appelle l'origine. C'est le point où l'axe x et l'axe y se croisent.
Nous utilisons les coordonnées pour localiser un point sur le plan xy. Tracons le point à\((1,3)\) titre d'exemple. Tout d'abord, localisez 1 sur l'axe x et tracez légèrement une ligne verticale passant par x=1x=1. Localisez ensuite 3 sur l'axe y et tracez une ligne horizontale passant par y=3y=3. Maintenant, trouvez le point où ces deux lignes se rencontrent, c'est-à-dire le point avec les coordonnées\((1,3)\).
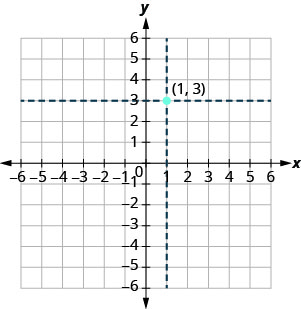
Notez que la ligne verticale\(x=1\) et la ligne horizontale ne\(y=3\) font pas partie du graphique. Nous les avons simplement utilisés pour nous aider à localiser le point\((1,3)\).
Tracez chaque point du système de coordonnées rectangulaires et identifiez le quadrant dans lequel se trouve le point :
- (−5,4)
- (−3, −4)
- (2, −3)
- (−2,3)
- \((3, \frac{5}{2})\)
- Réponse
-
Le premier numéro de la paire de coordonnées est la coordonnée x et le second est la coordonnée y.
- Puisque x=−5, le point se trouve à gauche de l'axe y. De plus, puisque y=4, le point se trouve au-dessus de l'axe x. Le point (−5,4) se trouve dans le quadrant II.
- Puisque x=−3, le point se trouve à gauche de l'axe y. De plus, puisque y=−4, le point se trouve en dessous de l'axe x. Le point (−3, −4) se trouve dans le quadrant III.
- Puisque x=2, le point se trouve à droite de l'axe y. Puisque y=−3, le point se trouve en dessous de l'axe X. Le point (2, -3) se trouve dans le quadrant lV.
- Puisque x=−2, le point se trouve à gauche de l'axe y. Puisque y=3, le point se trouve au-dessus de l'axe X. Le point (−2,3) se trouve dans le quadrant II.
- Puisque x=3, le point se trouve à droite de l'axe y. Depuis\(y = \frac{5}{2}\), le point se trouve au-dessus de l'axe X. (Il peut être utile d'écrire\(\frac{5}{2}\) sous forme de nombre mixte ou décimal.) Le point\((3, \frac{5}{2})\) se trouve dans le quadrant I.
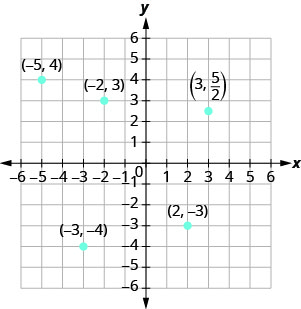
Figurine\(\PageIndex{4}\)
Tracez chaque point dans un système de coordonnées rectangulaires et identifiez le quadrant dans lequel se trouve le point :
- (−2,1)
- (−3, −1)
- (4, −4)
- (−4,4)
- \((-4, \frac{3}{2})\)
- Réponse
-
Tracez chaque point dans un système de coordonnées rectangulaires et identifiez le quadrant dans lequel se trouve le point :
- (−4,1)
- (−2,3)
- (2, −5)
- (−2,5)
- \((-3, \frac{5}{2})\)
- Réponse
-
Comment les signes affectent-ils la localisation des points ? Vous avez peut-être remarqué certaines tendances lorsque vous avez représenté les points dans l'exemple précédent.
Pour ce qui est du point\(\PageIndex{4}\) de la figure du quadrant IV, que remarquez-vous à propos des signes des coordonnées ? Qu'en est-il des signes des coordonnées des points du troisième quadrant ? Le deuxième quadrant ? Le premier quadrant ?
Pouvez-vous le savoir simplement en regardant les coordonnées dans quel quadrant se trouve le point (−2,5) ? Dans quel quadrant se trouve (2, −5) ?
Nous pouvons résumer les modèles de signes des quadrants de cette manière.
\[\begin{array}{ccc}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\]
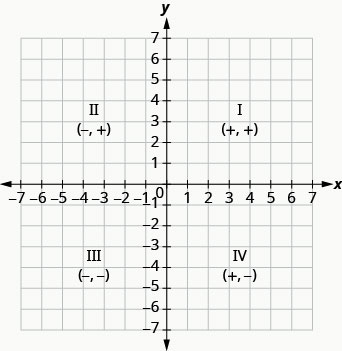
Et si une coordonnée est égale à zéro, comme indiqué sur la figure\(\PageIndex{6}\) ? Où se trouve le point (0,4) ? Où se trouve le point (−2,0) ?
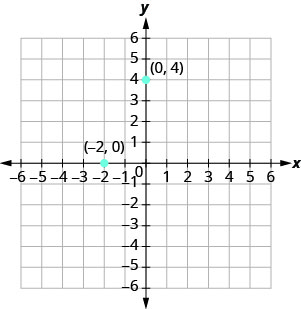
Le point (0,4) se trouve sur l'axe des y et le point (−2,0) sur l'axe des x.
Les points dont la coordonnée y est égale à 0 se trouvent sur l'axe x et ont des coordonnées (a,0).
Les points dont la coordonnée x est égale à 0 se trouvent sur l'axe y et ont des coordonnées (0, b).
Tracez chaque point :
- (0,5)
- (4,0)
- (−3,0)
- (0,0)
- (0, -1)
- Réponse
-
- Puisque x=0, le point dont les coordonnées sont (0,5) se trouve sur l'axe y.
- Puisque y=0, le point dont les coordonnées sont (4,0) se trouve sur l'axe des x.
- Puisque y=0, le point dont les coordonnées sont (−3,0) se trouve sur l'axe des x.
- Puisque x=0 et y=0, le point dont les coordonnées sont (0,0) est l'origine.
- Puisque x=0, le point dont les coordonnées sont (0, -1) se trouve sur l'axe y.
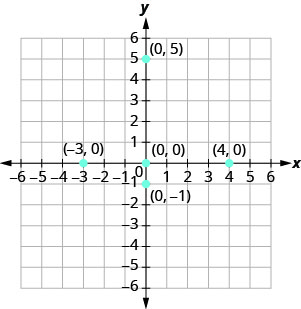
Figurine\(\PageIndex{7}\)
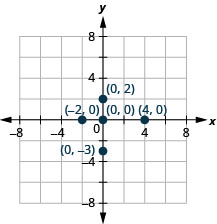
Tracez chaque point :
- (4,0)
- (−2,0)
- (0,0)
- (0,2)
- (0, −3).
- Réponse
-
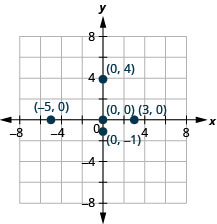
Tracez chaque point :
- (−5,0)
- (3,0)
- (0,0)
- (0, -1)
- (0,4).
- Réponse
-
En algèbre, il est tout aussi important de pouvoir identifier les coordonnées d'un point affiché sur un graphique que de tracer des points. Pour identifier la coordonnée x d'un point sur un graphique, lisez le nombre sur l'axe x directement au-dessus ou en dessous du point. Pour identifier la coordonnée y d'un point, lisez le nombre sur l'axe y directement à gauche ou à droite du point. N'oubliez pas que lorsque vous écrivez la paire ordonnée, utilisez le bon ordre (x, y).
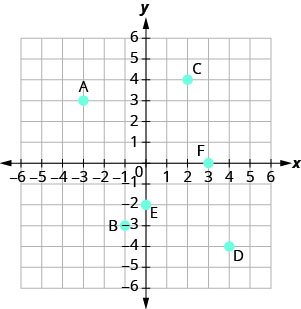
Nommez la paire ordonnée de chaque point indiqué dans le système de coordonnées rectangulaires.
- Réponse
-
Le point A se trouve au-dessus de −3 sur l'axe x, de sorte que la coordonnée x du point est −3.
Le point se trouve à gauche de 3 sur l'axe y, de sorte que la coordonnée y du point est 3. - Les coordonnées du point sont (−3,3).
-
Le point B se trouve en dessous de -1 sur l'axe x, de sorte que la coordonnée x du point est -1.
Le point se trouve à gauche de −3 sur l'axe y, de sorte que la coordonnée y du point est −3. - Les coordonnées du point sont (−1, −3).
Le point C se trouve au-dessus de 2 sur l'axe x, de sorte que la coordonnée x du point est 2.
Le point se trouve à droite de 4 sur l'axe y, de sorte que la coordonnée y du point est 4. - Les coordonnées du point sont (2,4).
- Le point D se trouve en dessous de 4 sur l'axe x, de sorte que la coordonnée x du point est 4.
- Le point se trouve à droite de −4 sur l'axe y, de sorte que la coordonnée y du point est −4.
- Les coordonnées du point sont (4, −4).
-
Le point E se trouve sur l'axe y à y=−2. Les coordonnées du point E sont (0, −2).
Le point F se trouve sur l'axe x à x=3. Les coordonnées du point F sont (3,0).
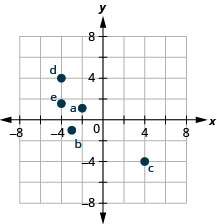
Nommez la paire ordonnée de chaque point indiqué dans le système de coordonnées rectangulaires.
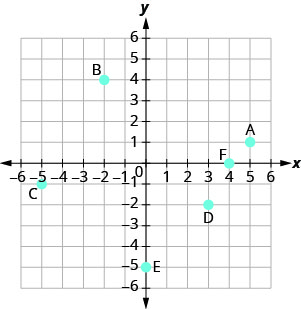
- Réponse
-
A : (5,1) B : (−2,4) C : (−5, −1) D : (3, −2) E : (0, −5) F : (4,0)
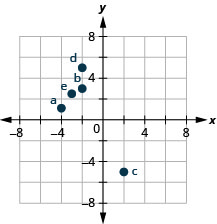
Nommez la paire ordonnée de chaque point indiqué dans le système de coordonnées rectangulaires.
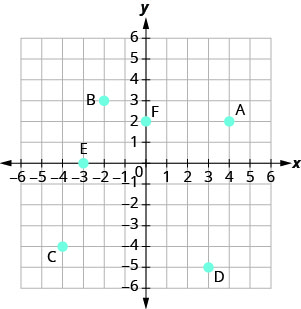
- Réponse
-
A : (4,2) B : (−2,3) C : (−4, −4) D : (3, −5) E : (−3,0) F : (0,2)
Vérifier les solutions à une équation à deux variables
Jusqu'à présent, toutes les équations que vous avez résolues étaient des équations avec une seule variable. Dans presque tous les cas, lorsque vous avez résolu l'équation, vous avez obtenu exactement une solution. Le processus de résolution d'une équation s'est terminé par une déclaration telle que x=4. (Ensuite, vous avez vérifié la solution en la replaçant dans l'équation.)
Voici un exemple d'équation dans une variable, et sa solution unique.
\[\begin{aligned} 3 x+5 &=17 \\ 3 x &=12 \\ x &=4 \end{aligned}\]
Mais les équations peuvent comporter plusieurs variables. Les équations à deux variables peuvent être de la forme Ax+By=C. Les équations de cette forme sont appelées équations linéaires à deux variables.
Une équation de la forme Ax+By=C, où A et B ne sont pas tous deux nuls, est appelée équation linéaire à deux variables.
Remarquez la ligne de mots en linéaire. Voici un exemple d'équation linéaire à deux variables, x et y.
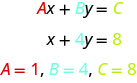
L'équation y=−3x+5 est également une équation linéaire. Mais elle ne semble pas avoir la forme Ax+By=C. Nous pouvons utiliser la propriété d'addition d'égalité et la réécrire sous la forme Ax+By=C.
\(\begin{array}{llll} {} &{y} &{=} &{-3x + 5} \\ {\text{Add to both sides.}} &{y + 3x } &{=} &{-3x + 5 + 3x} \\{\text{Simplify.}} &{y + 3x} &{=} &{5} \\{\text{Use the Commutative Property to put it in}} &{3x + y} &{=} &{5} \\{Ax+By = C\text{ form.}} &{} &{} &{} \end{array}\)
En réécrivant y=−3x+5 en 3x+y=5, nous pouvons facilement voir qu'il s'agit d'une équation linéaire à deux variables car elle est de la forme Ax+By=C. Lorsqu'une équation est de la forme Ax+By=C, nous disons qu'elle est sous forme standard.
Une équation linéaire est sous forme standard lorsqu'elle est écrite Ax+By=C.
La plupart des gens préfèrent que A, B et C soient des nombres entiers et qu'\(A\geq 0\)ils écrivent une équation linéaire sous forme standard, bien que cela ne soit pas strictement nécessaire.
Les équations linéaires offrent une infinité de solutions. Pour chaque nombre substitué à x, il existe une valeur y correspondante. Cette paire de valeurs est une solution à l'équation linéaire et est représentée par la paire ordonnée (x, y). Lorsque nous substituons ces valeurs de x et de y dans l'équation, le résultat est une déclaration vraie, car la valeur du côté gauche est égale à la valeur du côté droit.
Une paire ordonnée (x, y) est une solution de l'équation linéaire Ax+By=C, si l'équation est une déclaration vraie lorsque les valeurs x et y de la paire ordonnée sont substituées dans l'équation.
Déterminez quelles paires ordonnées sont des solutions à l'équation x+4y=8.
(a) (0,2)
(b) (2, −4)
(c) (−4,3)
- Réponse
-
Substituez les valeurs x et y de chaque paire ordonnée dans l'équation et déterminez si le résultat est une déclaration vraie.
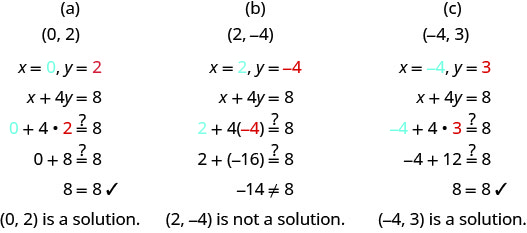
Parmi les paires ordonnées suivantes, lesquelles sont des solutions à 2x+3y=6 ?
- (3,0)
- (2,0)
- (6, −2)
- Réponse
-
1, 3
Parmi les paires ordonnées suivantes, lesquelles sont des solutions à l'équation 4x−y=8 ?
- (0,8)
- (2,0)
- (1, −4)
- Réponse
-
2, 3
Parmi les paires ordonnées suivantes, lesquelles sont des solutions à l'équation y=5x−1 ?
(a) (0, −1)
(b) (1,4)
(c) (−2, −7)
- Réponse
-
Substituez les valeurs x et y de chaque paire ordonnée dans l'équation et déterminez si cela donne lieu à une déclaration vraie.
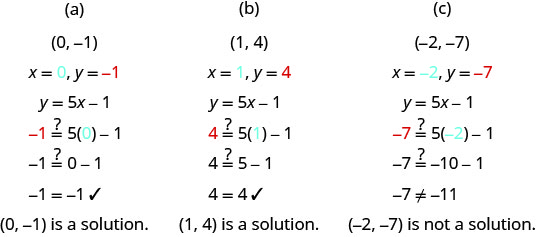
Parmi les paires ordonnées suivantes, lesquelles sont des solutions à l'équation y=4x−3 ?
- (0,3)
- (1,1)
- (−1, −1)
- Réponse
-
2
Parmi les paires ordonnées suivantes, lesquelles sont des solutions à l'équation y=−2x+6 ?
- (0,6)
- (1,4)
- (−2, −2)
- Réponse
-
1, 2
Compléter un tableau des solutions à une équation linéaire à deux variables
Dans les exemples ci-dessus, nous avons substitué les valeurs x et y d'une paire ordonnée donnée afin de déterminer s'il s'agissait ou non d'une solution à une équation linéaire. Mais comment trouver les paires commandées si elles ne sont pas données ? C'est plus simple que vous ne le pensez : vous pouvez simplement sélectionner une valeur pour xx, puis résoudre l'équation pour yy. Vous pouvez également choisir une valeur pour yy, puis résoudre pour xx.
Nous allons commencer par examiner les solutions à l'équation y = 5x−1 que nous avons trouvées dans l'exercice\(\PageIndex{13}\). Nous pouvons résumer ces informations dans un tableau de solutions, comme indiqué dans le tableau\(\PageIndex{1}\).
| y=5x−1 | ||
| x | y | (x, y) |
| 0 | −1 | (0, -1) |
| 1 | 4 | (1,4) |
Pour trouver une troisième solution, nous allons laisser x=2 et résoudre pour y.
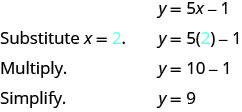
La paire ordonnée (2,9) est une solution à y=5x−1. Nous l'ajouterons au tableau\(\PageIndex{2}\).
| y=5x−1 | ||
| x | y | (x, y) |
| 0 | −1 | (0, -1) |
| 1 | 4 | (1,4) |
| 2 | 9 | (2,9) |
Nous pouvons trouver d'autres solutions à l'équation en substituant n'importe quelle valeur de x ou n'importe quelle valeur de y et en résolvant l'équation résultante pour obtenir une autre paire ordonnée qui est une solution. Il existe une infinité de solutions à cette équation.
Compléter le tableau pour trouver trois solutions à l'équation y=4x−2.
| y=4x−2 | ||
| x | y | (x, y) |
| 0 | ||
| −1 | ||
| 2 | ||
- Réponse
-
Remplacez x=0, x=−1 et x=2 par y=4x−2.
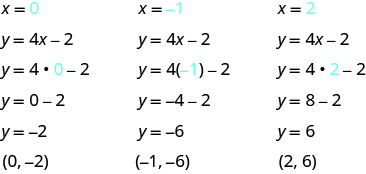
-
Les résultats sont résumés dans le tableau\(\PageIndex{4}\).
y=4x−2 x y (x, y) 0 −2 (0, −2) −1 −6 (−1, −6) 2 6 (2,6) Tableau\(\PageIndex{4}\)
Complétez le tableau pour trouver trois solutions à cette équation : y=3x−1.
| y=3x−1 | ||
| x | y | (x, y) |
| 0 | ||
| −1 | ||
| 2 | ||
- Réponse
-
y=3x−1 x y (x, y) 0 -1 (0, -1) −1 -4 (-1, -4) 2 5 (2, 5) Tableau\(\PageIndex{6}\)
Complétez le tableau pour trouver trois solutions à cette équation : y=6x+1.
| y = 6 x +1 | ||
| x | y | (x, y) |
| -2 | ||
- Réponse
-
y = 6 x +1 x y (x, y) 0 1 (0,1) 1 7 (1,7) −2 −11 (−2, −11) Tableau\(\PageIndex{8}\)
Compléter\(\PageIndex{9}\) le tableau pour trouver trois solutions à l'équation 5x−4y=20.
| 5x−4 y=20 | ||
| x | y | (x, y) |
| 0 | ||
| 5 | ||
- Réponse
-
Substituez la valeur donnée dans l'équation 5x−4y=20 et résolvez pour l'autre variable. Renseignez ensuite les valeurs du tableau.
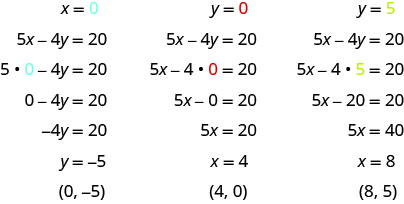
-
Les résultats sont résumés dans le tableau\(\PageIndex{10}\).
5x−4 y=20 x y (x, y) 0 −5 (0, −5) 4 0 (4,0) 8 5 (8,5) Tableau\(\PageIndex{10}\)
Complétez le tableau pour trouver trois solutions à cette équation : 2x−5y=20.
| 2x−5 y=20 | ||
| x | y | (x, y) |
| -5 | ||
- Réponse
-
2x−5 y=20 x y (x, y) 0 −4 (0, −4) 10 0 (10,0) −5 −6 (−5, −6) Tableau\(\PageIndex{12}\)
Complétez le tableau pour trouver trois solutions à cette équation : 3x−4y=12.
| 3x−4 y=12 | ||
| x | y | (x, y) |
| -4 | ||
- Réponse
-
3x−4 y=12 x y (x, y) 0 −3 (0, −3) 4 0 (4,0) −4 −6 (−4, −6) Tableau\(\PageIndex{14}\)
Trouver des solutions à une équation linéaire
Pour trouver une solution à une équation linéaire, vous pouvez sélectionner n'importe quel nombre que vous souhaitez remplacer dans l'équation pour x ou y. Mais comme vous devrez utiliser ce nombre pour résoudre l'autre variable, il est conseillé de choisir un nombre facile à utiliser.
Lorsque l'équation est sous forme y, avec le y seul sur un côté de l'équation, il est généralement plus facile de choisir les valeurs de x, puis de les résoudre pour y.
Trouvez trois solutions à l'équation y=−3x+2.
- Réponse
-
Nous pouvons remplacer x par n'importe quelle valeur ou y par n'importe quelle valeur. Comme l'équation est sous forme y, il sera plus facile de la remplacer par des valeurs de x. Choisissons x=0, x=1 et x=−1.



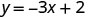
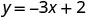
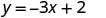
Substituez la valeur dans l'équation. 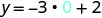
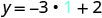
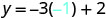
Simplifiez. 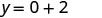
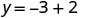
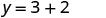
Simplifiez. 
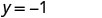

Écrivez la paire commandée. (0, 2) (1, -1) (-1, 5) Vérifiez. y=−3 x +2 y=−3 x +2 y=−3 x +2 \(2 \stackrel{?}{=} -3 \cdot 0 + 2\) \(-1 \stackrel{?}{=} -3 \cdot 1 + 2\) \(5 \stackrel{?}{=} -3 (-1) + 2\) \(2 \stackrel{?}{=} 0 + 2\) \(-1 \stackrel{?}{=} -3 + 2\) \(5 \stackrel{?}{=} -3 + 2\) \(2 = 2\checkmark\) \(-1 = -1\checkmark\) \(5 = 5\checkmark\) - Tableau\(\PageIndex{15}\)
-
Ainsi, (0,2), (1, -1) et (−1,5) sont toutes des solutions à y=−3x+2. Nous les montrons dans le tableau\(\PageIndex{16}\).
y=−3 x +2 x y (x, y) 0 2 (0,2) 1 −1 (1, -1) −1 5 (−1,5) Tableau\(\PageIndex{16}\)
Trouvez trois solutions à cette équation : y=−2x+3.
- Réponse
-
Les réponses peuvent varier.
Trouvez trois solutions à cette équation : y=−4x+1.
- Réponse
-
Les réponses peuvent varier.
Nous avons vu comment l'utilisation de zéro comme valeur de x permet de trouver facilement la valeur de y. Lorsqu'une équation est sous forme standard, avec x et y du même côté de l'équation, il est généralement plus facile de trouver d'abord une solution lorsque x=0, de trouver une deuxième solution lorsque y=0, puis de trouver une troisième solution.
Trouvez trois solutions à l'équation 3x+2y=6.
- Réponse
-
Nous pouvons remplacer x par n'importe quelle valeur ou y par n'importe quelle valeur. Comme l'équation est sous forme standard, choisissons d'abord x=0, puis y=0, puis trouvons un troisième point.

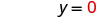

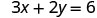
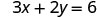
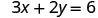
Substituez la valeur dans l'équation. 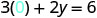
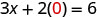
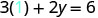
Simplifiez. 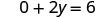
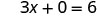
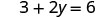
Résoudre. 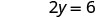
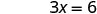
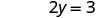
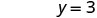

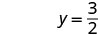
Écrivez la paire commandée. (0, 3) (2, 0) \((1,\frac{3}{2})\) Vérifiez. 3 x 2 y = 6 3 x 2 y = 6 3 x 2 y = 6 \(3\cdot 0 + 2\cdot 3 \stackrel{?}{=} 6\) \(3\cdot 2 + 2\cdot 0 \stackrel{?}{=} 6\) \(3\cdot 1 + 2\cdot \frac{3}{2} \stackrel{?}{=} 6\) \(0 + 6 \stackrel{?}{=} 6\) \(6 + 0 \stackrel{?}{=} 6\) \(3 + 3 \stackrel{?}{=} 6\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) \(6 = 6\checkmark\) Tableau\(\PageIndex{17}\) Donc (0,3), (2,0) et\((1,\frac{3}{2})\) sont toutes des solutions à l'équation 3x+2y=6. Nous pouvons répertorier ces trois solutions dans le tableau\(\PageIndex{18}\).
3x+2 ans = 63 x+2 ans = 6 x y (x, y) 0 3 (0,3) 2 0 (2,0) 1 \(\frac{3}{2}\) \((1, \frac{3}{2})\) Tableau\(\PageIndex{18}\)
Trouvez trois solutions à l'équation 2x+3y=6.
- Réponse
-
Les réponses peuvent varier.
Trouvez trois solutions à l'équation 4x+2y=8.
- Réponse
-
Les réponses peuvent varier.
Concepts clés
- Modèles de signes des quadrants
\(\begin{array}{ll}{\text { Quadrant I }} & {\text { Quadrant II }} & {\text { Quadrant III }} & {\text { Quadrant IV }} \\ {(x, y)} & {(x, y)} & {(x, y)} & {(x, y)} \\ {(+,+)} & {(-,+)} & {(-,-)} & {(+,-)}\end{array}\) - Points sur les axes
- Sur l'axe x, y=0. Les points dont la coordonnée y est égale à 0 se trouvent sur l'axe x et ont des coordonnées (a,0).
- Sur l'axe y, x=0. Les points dont la coordonnée x est égale à 0 se trouvent sur l'axe y et ont des coordonnées (0, b).
- Solution d'une équation linéaire
- Une paire ordonnée (x, y) est une solution de l'équation linéaire Ax+By=C, si l'équation est une déclaration vraie lorsque les valeurs x et y de la paire ordonnée sont substituées dans l'équation.
Lexique
- équation linéaire
- Une équation linéaire de la forme Ax+By=C, où A et B ne sont pas tous les deux nuls, est appelée équation linéaire à deux variables.
- paire commandée
- Une paire ordonnée (x, y) donne les coordonnées d'un point dans un système de coordonnées rectangulaires.
- origine
- Le point (0,0) (0,0) est appelé origine. C'est le point où l'axe x et l'axe y se croisent.
- quadrant
- L'axe x et l'axe y divisent un plan en quatre régions, appelées quadrants.
- système de coordonnées rectangulaires
- Un système de grille est utilisé en algèbre pour montrer une relation entre deux variables ; également appelé plan xy ou « plan de coordonnées ».
- coordonnée x
- Le premier nombre d'une paire ordonnée (x, y).
- Y -coordonnée
- Le deuxième nombre d'une paire ordonnée (x, y).


