3.5 : Résolvez des applications à mouvement uniforme
- Page ID
- 194877
À la fin de cette section, vous serez en mesure de :
- Résolvez des applications de mouvement
Avant de commencer, répondez à ce questionnaire de préparation.
- Trouvez la distance parcourue par une voiture parcourant 70 miles par heure pendant 3 heures.
Si vous avez oublié ce problème, passez en revue l'exercice 2.6.1. - Résoudre\(x+1.2(x−10)=98\).
Si vous avez oublié ce problème, passez en revue l'exercice 2.4.7. - Convertissez 90 minutes en heures.
Si vous avez oublié ce problème, passez en revue l'exercice 1.11.1.
Résolvez des applications de mouvements
Lors de la planification d'un voyage en voiture, il est souvent utile de savoir combien de temps il faudra pour atteindre la destination ou quelle distance parcourir chaque jour. Nous utiliserions la formule de distance, de vitesse et de temps, d=RT, que nous avons déjà vue.
Dans cette section, nous utiliserons cette formule dans des situations qui nécessitent un peu plus d'algèbre à résoudre que celles que nous avons vues précédemment. En général, nous chercherons à comparer deux scénarios, tels que deux véhicules circulant à des vitesses différentes ou dans des directions opposées. Lorsque la vitesse de chaque véhicule est constante, nous appelons des applications comme celle-ci à des problèmes de mouvement uniforme.
Nos stratégies de résolution de problèmes s'appliqueront toujours ici, mais nous ajouterons à la première étape. La première étape consistera à dessiner un diagramme qui montre ce qui se passe dans l'exemple. Dessiner le diagramme nous aide à comprendre ce qui se passe afin d'écrire une équation appropriée. Ensuite, nous allons créer un tableau pour organiser les informations, comme nous l'avons fait pour les demandes d'argent.
Les étapes sont répertoriées ici pour faciliter la consultation :
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
- Dessinez un diagramme pour illustrer ce qui se passe.
- Créez un tableau pour organiser les informations.
- Étiquetez les colonnes : taux, temps, distance.
- Énumérez les deux scénarios.
- Écrivez les informations que vous connaissez.
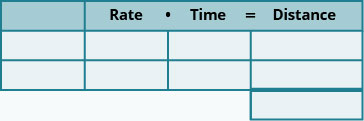
- Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
- Complétez le tableau.
- Utilisez des expressions variables pour représenter cette quantité sur chaque ligne.
- Multipliez le taux par le temps nécessaire pour obtenir la distance.
- Traduisez en une équation.
- Réaffirmez le problème en une phrase avec toutes les informations importantes.
- Traduisez ensuite la phrase en équation.
- Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
Un train express et un train local partent de Pittsburgh pour se rendre à Washington, D.C. Le train express peut faire le trajet en 4 heures et le train local prend 5 heures pour le trajet. La vitesse du train express est de 20 miles par heure plus rapide que la vitesse du train local. Déterminez la vitesse des deux trains.
- Réponse
-
Étape 1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
Dessinez un diagramme pour illustrer ce qui se passe. Vous trouverez ci-dessous une esquisse de ce qui se passe dans l'exemple.
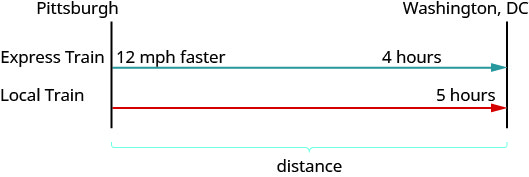
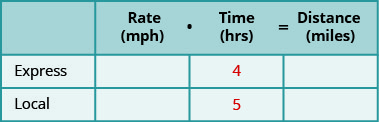
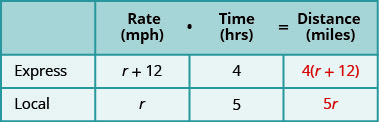
Créez un tableau pour organiser les informations. Étiquetez les colonnes « Taux », « Temps » et « Distance ». Énumérez les deux scénarios. Écrivez les informations que vous connaissez.
Étape 2. Identifiez ce que nous recherchons.
On nous demande de connaître la vitesse des deux trains. Notez que la formule de distance utilise le mot « taux », mais qu'il est plus courant d'utiliser « vitesse » lorsque nous parlons de véhicules en anglais courant.
Étape 3. Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
Compléter le tableau Utilisez des expressions variables pour représenter cette quantité sur chaque ligne. Nous cherchons la vitesse des trains. Laissons r représenter la vitesse du train local. Comme la vitesse du train express est plus rapide de 12 mi/h, nous la représentons par r+12.
\[\begin{aligned} r &=\text { speed of the local train } \\ r+12 &=\text { speed of the express train } \end{aligned}\]
Renseignez les vitesses dans le tableau.
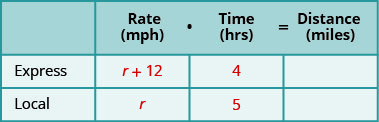
-
Multipliez le taux par le temps nécessaire pour obtenir la distance.
Étape 4. Traduisez en une équation.
Réaffirmez le problème en une phrase avec toutes les informations importantes. Traduisez ensuite la phrase en équation. 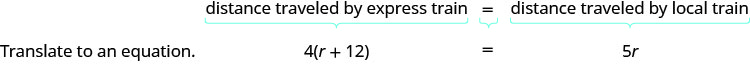
-
- L'équation pour modéliser cette situation proviendra de la relation entre les distances. Regardez le schéma que nous avons dessiné ci-dessus. Comment la distance parcourue par le train express est-elle liée à la distance parcourue par le train local ?
- Comme les deux trains partent de Pittsburgh et se rendent à Washington, D.C. ils parcourent la même distance. Nous écrivons donc :
Étape 5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
Étape 6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique. \[\begin{array}{ll}{\text { express train }} & {60 \mathrm{mph}(4 \text { hours })=240 \mathrm{miles}} \\ {\text { local train }} & {48 \mathrm{mph}(5 \text { hours })=240 \mathrm{miles} \checkmark \end{array}\]Maintenant, résolvez cette équation. 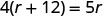
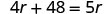
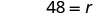
La vitesse du train local est donc de 48 mi/h.
Déterminez la vitesse du train express. 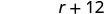


La vitesse du train express est de 600 mi/h.
Étape 7. Répondez à la question par une phrase complète.
La vitesse du train local est de 48 mi/h et celle du train express est de 60 mi/h.
Wayne et Dennis aiment emprunter la piste cyclable qui relie Riverside Park à la plage. La vitesse de Dennis est plus rapide de 11 miles à l'heure que celle de Wayne, il faut donc 2 heures à Wayne pour se rendre à la plage tandis que Dennis met 1,5 heure pour le trajet. Trouvez la vitesse des deux motards.
- Réponse
-
Wayne 21 mi/h, Dennis 28 mi/h
Jeromy peut se rendre de sa maison de Cleveland à son université de Chicago en 4,5 heures de route. Il faut 6 heures à sa mère pour faire le même trajet. Jeromy roule 20 miles à l'heure plus vite que sa mère. Trouvez la vitesse de Jeromy et celle de sa mère.
- Réponse
-
Jeromy 80 mi/h, mère 60 mi/h
Dans Exercice\(\PageIndex{4}\), le dernier exemple, nous avions deux trains qui parcouraient la même distance. Le diagramme et le graphique nous ont aidés à écrire l'équation que nous avons résolue. Voyons comment cela fonctionne dans un autre cas.
Christopher et ses parents vivent à 115 miles l'un de l'autre. Ils se sont rencontrés dans un restaurant situé entre leurs maisons pour fêter l'anniversaire de sa mère. Christopher a conduit une heure et demie tandis que ses parents ont fait 1 heure pour se rendre au restaurant. La vitesse moyenne de Christopher était 10 milles à l'heure plus rapide que la vitesse moyenne de ses parents. Quelle était la vitesse moyenne de Christopher et de ses parents lorsqu'ils se rendaient au restaurant ?
- Réponse
-
Étape 1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
Dessinez un diagramme pour illustrer ce qui se passe. Vous trouverez ci-dessous une esquisse de ce qui se passe dans l'exemple.
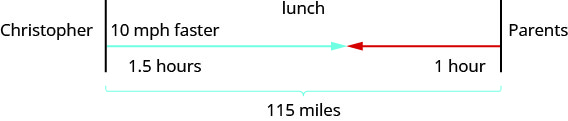
Créez un tableau pour organiser les informations.
Étiquetez les colonnes : taux, temps, distance.
Énumérez les deux scénarios.
Écrivez les informations que vous connaissez.
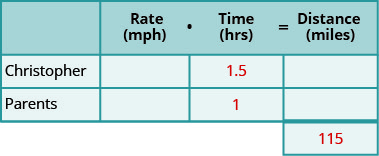
Étape 2. Identifiez ce que nous recherchons.
On nous demande de connaître les vitesses moyennes de Christopher et de ses parents.
Étape 3. Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
Complétez le tableau. - Utilisez des expressions variables pour représenter cette quantité sur chaque ligne.
- Nous recherchons leurs vitesses moyennes. Supposons que r représente la vitesse moyenne des parents. Puisque la vitesse du Christopher est 10 mi/h plus rapide, nous la représentons par r+10.
-
Renseignez les vitesses dans le tableau.
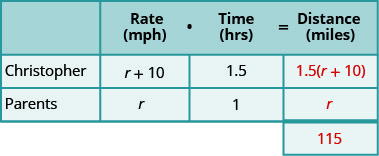
Multipliez le taux par le temps nécessaire pour obtenir la distance.
Étape 4. Traduisez en une équation.
Réaffirmez le problème en une phrase avec toutes les informations importantes. Traduisez ensuite la phrase en équation. Encore une fois, nous devons identifier une relation entre les distances afin d'écrire une équation. Regardez le diagramme que nous avons créé ci-dessus et remarquez la relation entre la distance parcourue par Christopher et la distance parcourue par ses parents.La distance parcourue par Christopher et la distance parcourue par ses parents doivent totaliser 115 miles. Nous écrivons donc :

Étape 5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
\(\begin{array} {cc} {} &{1.5(r + 10) + r = 115} \\ {} &{1.5r + 15 + r = 115} \\ {\text{Now solve this equation.}} &{2.5r + 15 = 115} \\{} &{2.5r = 100} \\{} &{r = 40} \\ {} &{\text{so the parents' speed was 40 mph.}} \\ {} &{r + 10} \\ {\text{Christopher's speed is r + 10}} &{40 + 10} \\ {} &{50} \\ {} &{\text{Christopher's speed was 50 mph.}} \\ {} &{} \end{array}\)
Étape 6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
\(\begin{array}{llll} {\text{Christopher drove}} &{50\text{ mph (1.5 hours)}} &{=} &{75\text{ miles}}\\ {\text{His parents drove}} &{40\text{ mph (1 hour)}} &{=} &{\underline{40 \text{ miles}}}\\ {} &{} &{} &{115\text{ miles}} \end{array}\)
\(\begin{array}{ll} {\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{} \\{} &{\text{Christopher's speed was 50 mph.}}\\ {} &{\text{His parents' speed was 40 mph.}} \end{array}\)
Carina se rend en voiture de son domicile d'Anaheim à Berkeley le jour même où son frère se rend de Berkeley à Anaheim. Ils décident donc de se retrouver pour déjeuner en cours de route à Buttonwillow. La distance entre Anaheim et Berkeley est de 410 miles. Carina met 3 heures pour se rendre à Buttonwillow, tandis que son frère fait 4 heures de route pour s'y rendre. La vitesse moyenne parcourue par le frère de Carina était de 24 milles à l'heure plus rapide que la vitesse moyenne de Carina. Trouvez la vitesse moyenne de Carina et de son frère.
- Réponse
-
Carina 50 mi/h, frère 65 mi/h
Ashley va à l'université de Minneapolis, à 234 miles de chez elle à Sioux Falls. Elle veut que ses parents lui apportent plus de vêtements d'hiver, alors ils décident de se retrouver dans un restaurant sur la route entre Minneapolis et Sioux Falls. Ashley et ses parents ont tous deux conduit 2 heures jusqu'au restaurant. La vitesse moyenne d'Ashley était plus rapide de sept milles à l'heure que la vitesse moyenne de ses parents. Découvrez la vitesse moyenne d'Ashley et de ses parents.
- Réponse
-
parents 55 mi/h, Ashley 62 mi/h
En lisant l'exemple suivant, réfléchissez à la relation entre les distances parcourues. Lequel des deux exemples précédents ressemble le plus à cette situation ?
Deux camionneurs quittent une aire de repos sur l'autoroute en même temps. Un camion se déplace vers l'est et l'autre vers l'ouest. Le camion qui circule vers l'ouest se déplace à 70 mi/h et le camion qui se déplace vers l'est a une vitesse moyenne de 60 mi/h. Combien de temps vont-ils voyager avant d'être distants de 325 miles ?
- Réponse
-
Étape 1. Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
Dessinez un diagramme pour illustrer ce qui se passe.
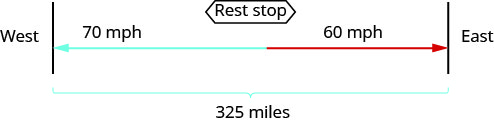
Créez un tableau pour organiser les informations.

Étape 2. Identifiez ce que nous recherchons.
On nous demande de déterminer la durée pendant laquelle les camions se déplaceront jusqu'à ce qu'ils soient distants de 325 milles.
Étape 3. Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
Nous recherchons le temps parcouru. Les deux camions parcourront le même temps. Appelons l'heure t. Comme leurs vitesses sont différentes, ils parcourront des distances différentes. Complétez le tableau.
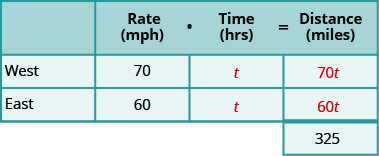
Étape 4. Traduisez en une équation.
Nous devons trouver une relation entre les distances afin d'écrire une équation. En regardant le diagramme, quelle est la relation entre la distance parcourue par chacun des camions ? La distance parcourue par le camion en direction ouest plus la distance parcourue par le camion en direction est doivent totaliser 325 milles. Nous écrivons donc :

Étape 5. Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
\[\begin{array} {lrll} {\text{Now solve this equation. }} & {70 t+60 t} &{=} &{325} \\ {} &{130 t} &{=} &{325} \\ {} &{t} &{=} &{2.5} \end{array}\]
Étape 6. Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
\(\begin{array}{llll} {\text{Truck going West}} &{70\text{ mph (2.5 hours)}} &{=} &{175\text{ miles}}\\ {\text{Truck going East}} &{60\text{ mph (2.5 hour)}} &{=} &{\underline{150 \text{ miles}}}\\ {} &{} &{} &{325\text{ miles}} \end{array}\)
\(\begin{array}{ll} \\{\textbf{Step 7. Answer}\text{ the question with a complete sentence.}} &{\text{It will take the truck 2.5 hours to be 325 miles apart.}} \end{array}\)
Pierre et Monique quittent leur domicile de Portland au même moment. Pierre roule vers le nord sur l'autoroute à péage à une vitesse de 75 miles à l'heure tandis que Monique roule vers le sud à une vitesse de 110 miles à l'heure. Combien de temps leur faudra-t-il pour se trouver à 429 miles l'un de l'autre ?
- Réponse
-
3 heures
Thanh et Nhat quittent leur bureau de Sacramento en même temps. Thanh roule vers le nord sur l'I-5 à une vitesse de 112 miles par heure. Nhat roule vers le sud sur l'I-5 à une vitesse de 120 km/h. Combien de temps leur faudra-t-il pour être distants de 330 miles ?
- Réponse
-
2,2 heures
Il est important de s'assurer que les unités correspondent lorsque nous utilisons le taux de distance et la formule de temps. Par exemple, si le tarif est exprimé en miles par heure, l'heure doit être exprimée en heures.
Quand Katie Mae se rend à l'école à pied, cela lui prend 30 minutes. Si elle fait du vélo, cela lui prend 15 minutes. Sa vitesse est plus rapide de cinq kilomètres à l'heure lorsqu'elle fait du vélo que lorsqu'elle marche. Quelle est sa vitesse de marche et sa vitesse à vélo ?
- Réponse
-
Tout d'abord, nous dessinons un diagramme qui représente la situation pour nous aider à voir ce qui se passe.
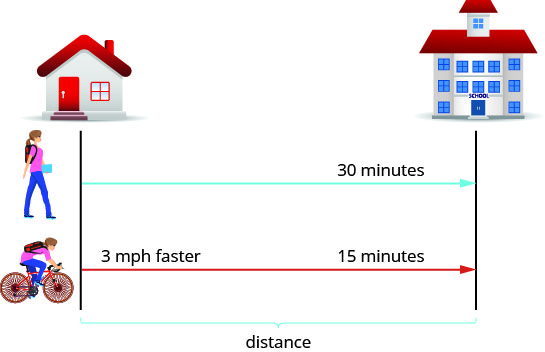
-
On nous demande de la trouver en train de marcher et de faire du vélo. Appelons-la vitesse de marche r. Comme sa vitesse de vélo est plus rapide de cinq kilomètres à l'heure, nous appellerons cette vitesse r+3. Nous écrivons les vitesses dans le graphique.
La vitesse est exprimée en miles par heure, nous devons donc également exprimer les temps en heures, pour que les unités soient les mêmes. N'oubliez pas qu'une heure équivaut à 60 minutes. Donc :
\[\begin{array}{l}{30 \text { minutes is } \frac{30}{60} \text { or } \frac{1}{2} \text { hour }} \\ {15 \text { minutes is } \frac{15}{60} \text { or } \frac{1}{4} \text { hour }}\end{array}\]
Ensuite, nous multiplions le taux par le temps pour remplir la colonne de distance.
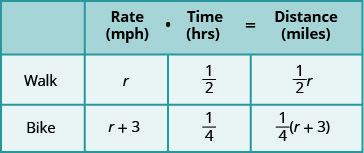
L'équation proviendra du fait que la distance entre le domicile de Katie Mae et son école est la même, qu'elle marche ou fasse du vélo.
Nous disons donc :

Traduisez en une équation. 
Résolvez cette équation. 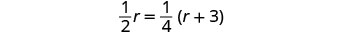
Effacez les fractions en multipliant par l'écran LCD toutes les fractions de l'équation. 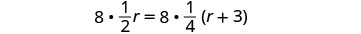
Simplifiez. 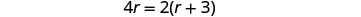
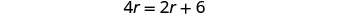


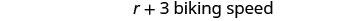

6 mi/h
(Katie) (vitesse de vélo de Mae)Nous allons vérifier si cela fonctionne.
Marchez 3 mi/h (0,5 heure) = 2,5 miles
Vélo 6 mi/h (0,25 heure) = 2,5 milesOui, de toute façon Katie Mae fait 2,5 km pour aller à l'école. La vitesse de marche de Katie Mae est de 3 mi/h.
Sa vitesse à vélo est de 6 mph.
Suzy met 50 minutes à pied pour monter du parking à la tour d'observation. Il lui faut 30 minutes pour redescendre jusqu'au parking. Sa vitesse en descente est de 2 milles à l'heure plus rapide que sa vitesse en montée. Découvrez les vitesses de montée et de descente de Suzy.
- Réponse
-
en montée 1,8 mi/h, en descente à trois mi/h
Llewyn met 45 minutes pour conduire son bateau en amont du quai jusqu'à son lieu de pêche préféré. Il lui faut 30 minutes pour reconduire le bateau vers l'aval jusqu'au quai. La vitesse du bateau en aval est de six milles à l'heure plus rapide que sa vitesse en amont. Déterminez les vitesses en amont et en aval du bateau.
- Réponse
-
en amont 8 mi/h, en aval 12 mi/h
Dans la formule de distance, de vitesse et de temps, le temps représente le temps réel écoulé (en heures, minutes, etc.). Si un problème nous donne les heures de début et de fin sous forme d'heures d'horloge, nous devons trouver le temps écoulé pour utiliser la formule.
Hamilton adore voyager à Las Vegas, à 255 miles de sa maison dans le comté d'Orange. Lors de son dernier voyage, il a quitté sa maison à 14 heures. La première partie de son voyage s'est déroulée sur les autoroutes de la ville encombrées. À 16 h, la circulation s'est dégagée et il a pu traverser le désert à une vitesse 1,75 fois plus rapide que lorsqu'il conduisait dans une zone encombrée. Il est arrivé à Las Vegas à 18 h 30. À quelle vitesse roulait-il à chaque étape de son voyage ?
- Réponse
-
Un schéma nous aidera à modéliser ce voyage.
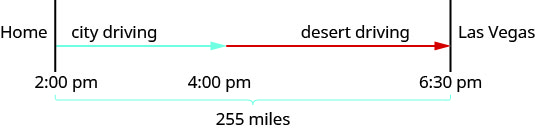
Ensuite, nous créons un tableau pour organiser les informations.
Nous savons que la distance totale est de 255 miles. Nous recherchons le taux de vitesse pour chaque partie du trajet. Le taux dans le désert est 1,75 fois plus élevé qu'en ville. Si on laisse r = le taux en ville, alors le taux dans le désert est de 1,75 r.
Les heures ici sont données sous forme d'heures d'horloge. Hamilton est parti de chez lui à 14 h 00 et est entré dans le désert à 16 h 30. Il a donc passé deux heures à parcourir les autoroutes encombrées de la ville. Puis il a roulé plus vite de 16 h 00 à 18 h 30 dans le désert. Il a donc roulé 2,5 heures dans le désert.
Maintenant, on multiplie les taux par le temps.
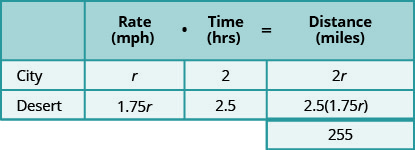
En regardant le schéma ci-dessous, nous pouvons voir que la somme de la distance parcourue en ville et de la distance parcourue dans le désert est de 255 miles.
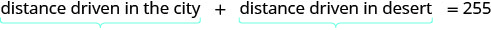
Traduisez en une équation. 
Résolvez cette équation. 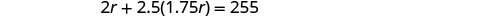
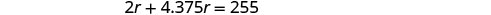
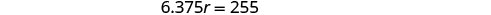
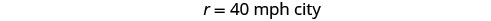
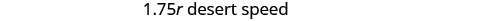
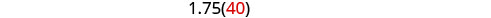
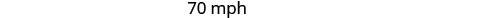
Vérifiez.

Hamilton a roulé 40 mi/h en ville et 70 mi/h dans le désert.
Cruz s'entraîne pour participer à un triathlon. Il a quitté sa maison à 6 heures et a couru jusqu'à 7 h 30. Puis il a roulé à vélo jusqu'à 9 h 45. Il a parcouru une distance totale de 51 milles. Sa vitesse en vélo était 1,6 fois supérieure à sa vitesse en course à pied. Découvrez les vitesses de course et de vélo de Cruz.
- Réponse
-
vélo 16 mi/h, course à pied 10 mi/h
Phuong a quitté la maison à vélo à 10 heures. Il a roulé sur la rue plate jusqu'à 11 h 15, puis a monté la colline jusqu'à 11 h 45. Il a parcouru un total de 31 miles. Sa vitesse en montée était 0,6 fois supérieure à sa vitesse sur une rue plate. Trouvez son vélo de vitesse en montée et dans une rue plate.
- Réponse
-
montée 12 mi/h, rue plate 20 mi/h
Concepts clés
- Distance, fréquence et temps
- D = rt où D = distance, r = taux, t = temps
- Stratégie de résolution de problèmes : applications relatives à la distance, au taux et au temps
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.
Dessinez un diagramme pour illustrer ce qui se passe.
Créez un tableau pour organiser les informations : étiquetez les colonnes : taux, temps, distance. Énumérez les deux scénarios. Écrivez les informations que vous connaissez. - Identifiez ce que nous recherchons.
- Nommez ce que nous recherchons. Choisissez une variable pour représenter cette quantité.
Complétez le tableau.
Utilisez des expressions variables pour représenter cette quantité sur chaque ligne.
Multipliez le taux par le temps nécessaire pour obtenir la distance. - Traduisez en une équation.
Réaffirmez le problème en une phrase avec toutes les informations importantes.
Traduisez ensuite la phrase en une équation. - Résolvez l'équation en utilisant de bonnes techniques d'algèbre.
- Vérifiez la réponse au problème et assurez-vous qu'elle est logique.
- Répondez à la question par une phrase complète.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris.


