Chapitre 1 Exercices de révision
- Page ID
- 195263
Exercices de révision des
Présentation des nombres entiers
Utiliser la valeur de position avec un nombre entier
Dans les exercices suivants, trouvez la valeur de position de chaque chiffre.
26 915
- 1
- 2
- 9
- 5
- 6
- Réponse
-
- dizaines
- dix mille
- centaines
- uns
- des milliers
359 417
- 9
- 3
- 4
- 7
- 1
58 129 304
- 5
- 0
- 1
- 8
- 2
- Réponse
-
- dix millions
- dizaines
- cent milliers
- millions
- dix mille
9 430 286 157
- 6
- 4
- 9
- 0
- 5
Dans les exercices suivants, nommez chaque numéro.
6 104
- Réponse
-
six mille cent quatre
493 068
3 975 284
- Réponse
-
trois millions neuf cent soixante-quinze mille deux cent quatre-vingt-quatre
85 620 435
Dans les exercices suivants, écrivez chaque nombre sous la forme d'un nombre entier à l'aide de chiffres.
trois cent quinze
- Réponse
-
315
soixante-cinq mille neuf cent douze
quatre-vingt-dix millions quatre cent vingt-cinq mille seize
- Réponse
-
90 425 016
un milliard quarante-trois millions neuf cent vingt-deux mille trois cent onze
Dans les exercices suivants, arrondissez à la valeur de position indiquée.
Arrondir à la dizaine la plus proche.
- 407
- 8 564
- Réponse
-
- 410
- 8 560
Arrondir à la centaine la plus proche.
- 25 846
- 25 864
Dans les exercices suivants, arrondissez chaque chiffre au 1 cent 2 mille 3 dix mille le plus proche.
864 951
- Réponse
-
- 865 000 865 000
- 865 000 865 000
- 860 000
3 972 849
Identifier les multiples et les facteurs
Dans les exercices suivants, utilisez les tests de divisibilité pour déterminer si chaque nombre est divisible par 2, par 3, par 5, par 6 et par 10.
168
- Réponse
-
de 2,3,6
264
375
- Réponse
-
de 3,5
750
1430
- Réponse
-
par 2,5,10
1080
Trouvez les factorisations principales et les multiples les moins courants
Dans les exercices suivants, déterminez la factorisation principale.
420
- Réponse
-
2\(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)
115
225
- Réponse
-
3\(\cdot 3 \cdot 5 \cdot 5\)
2475
1560
- Réponse
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)
56
72
- Réponse
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)
168
252
- Réponse
-
\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
391
Dans les exercices suivants, trouvez le multiple le moins courant des nombres suivants à l'aide de la méthode des multiples.
6,15
- Réponse
-
30
60, 75
Dans les exercices suivants, trouvez le multiple le moins courant des nombres suivants à l'aide de la méthode des facteurs premiers.
24, 30
- Réponse
-
120
70, 84
Utiliser le langage de l'algèbre
Utiliser des variables et des symboles algébriques
Dans les exercices suivants, traduisez ce qui suit de l'algèbre vers l'anglais.
25−7
- Réponse
-
25 moins 7, la différence de vingt-cinq et sept
5\(\cdot 6\)
\(45 \div 5\)
- Réponse
-
45 divisé par 5, le quotient de quarante-cinq et cinq
x+8
\(42 \geq 27\)
- Réponse
-
quarante-deux est supérieur ou égal à vingt-sept
3 n = 24
\(3 \leq 20 \div 4\)
- Réponse
-
3 est inférieur ou égal à 20 divisé par 4, trois est inférieur ou égal au quotient de vingt et quatre
\(a \neq 7 \cdot 4\)
Dans les exercices suivants, déterminez s'il s'agit d'une expression ou d'une équation.
\(6 \cdot 3+5\)
- Réponse
-
expression
y−8=32
Simplifier les expressions en utilisant l'ordre des opérations
Dans les exercices suivants, simplifiez chaque expression.
\(3^{5}\)
- Réponse
-
243
\(10^{8}\)
Dans les exercices suivants, simplifiez
6+10/2+2
- Réponse
-
13
9+12/3+4
\(20 \div(4+6) \cdot 5\)
- Réponse
-
10
\(33 \div(3+8) \cdot 2\)
\(4^{2}+5^{2}\)
- Réponse
-
41
\((4+5)^{2}\)
Evaluer une expression
Dans les exercices suivants, évaluez les expressions suivantes.
9x+7 lorsque x=3
- Réponse
-
34
5x−4 lorsque x=6
\(x^{4}\)quand\(x=3\)
- Réponse
-
81
\(3^{x}\)quand\(x=3\)
\(x^{2}+5 x-8\)quand\(x=6\)
- Réponse
-
58
\(2 x+4 y-5\)quand
\(x=7, y=8\)
Simplifiez les expressions en combinant des termes similaires
Dans les exercices suivants, identifiez le coefficient de chaque terme.
12e
- Réponse
-
12
9\(x^{2}\)
Dans les exercices suivants, identifiez les termes similaires.
\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)
- Réponse
-
12\(3, n^{2}\) et 3\(n^{2}\)
\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)
Dans les exercices suivants, identifiez les termes de chaque expression.
\(11 x^{2}+3 x+6\)
- Réponse
-
\(11 x^{2}, 3 x, 6\)
\(22 y^{3}+y+15\)
Dans les exercices suivants, simplifiez les expressions suivantes en combinant des termes similaires.
17a+9a
- Réponse
-
26a
18 z+9 z
9x+3x+8
- Réponse
-
12 x 8
8a+5a+9
7p+6+5p−4
- Réponse
-
12 p+2
8x+7+4x−5
Traduire une phrase anglaise en une expression algébrique
Dans les exercices suivants, traduisez les phrases suivantes en expressions algébriques.
la somme de 8 et 12
- Réponse
-
8+12
la somme de 9 et 1
la différence entre x et 4
- Réponse
-
x−4
la différence entre x et 3
le produit de 6 et y
- Réponse
-
6 ans
le produit de 9 et y
Adele a acheté une jupe et un chemisier. La jupe coûte 15$ de plus que le chemisier. Soit bb le coût du chemisier. Écrivez une expression pour le coût de la jupe.
- Réponse
-
b+15
Marcella a 6 cousins garçons de moins que filles. Soit g le nombre de cousines. Écrivez une expression pour le nombre de cousins garçons.
Ajouter et soustraire des entiers
Utiliser les négatifs et les contraires des nombres entiers
Dans les exercices suivants, ordonnez chacune des paires de nombres suivantes en utilisant < or >.
- 6___2
- −7___4
- −9___−1
- 9___−3
- Réponse
-
- >
- <
- <
- >
- −5___1
- −4___−9
- 6___10
- 3___−8
Dans les exercices suivants, trouvez l'opposé de chaque chiffre.
- −8
- 1
- Réponse
-
- 8
- −1
- −2
- 6
Dans les exercices suivants, simplifiez.
− (−19)
- Réponse
-
19
− (−53)
Dans les exercices suivants, simplifiez.
−m quand
- m=3
- m=−3
- Réponse
-
- −3
- 3
−p quand
- p=6
- p=−6
Simplifier les expressions avec une valeur
Dans les exercices suivants, simplifiez.
- |7|
- |−25|
- |0|
- Réponse
-
- 7
- 25
- 0
- |5|
- |0|
- |−19|
Dans les exercices suivants, saisissez <, > ou = pour chacune des paires de nombres suivantes.
- −8___|−8|
- −|−2|___−2
- Réponse
-
- <
- =
- |−3|___−|−3|
- 4___−|−4|
Dans les exercices suivants, simplifiez.
|8−4|
- Réponse
-
4
|9−6|
8 (14−2|−2|)
- Réponse
-
80
6 (13−4|−2|)
Dans les exercices suivants, évaluez.
1. |x| lorsque x=−28
- Réponse
-
- 28
- 15
- ylorsque y=−37
- |−z| lorsque z=−24
Ajouter des entiers
Dans les exercices suivants, simplifiez chaque expression.
−200+65
- Réponse
-
−135
−150+45
2+ (−8) +6
- Réponse
-
0
4+ (−9) +7
PLUS DE 140 (−75) +67
- Réponse
-
132
−32+24+ (−6) +10
Soustraire des entiers
Dans les exercices suivants, simplifiez.
9−3
- Réponse
-
6
−5− (−1)
- 15−6
- PLUS DE 15 ANS (−6)
- Réponse
-
- 9
- 9
- 12−9
- PLUS DE 12 ANS (−9)
- 8− (−9)
- 8+9
- Réponse
-
- 17
- 17
- 4− (−4)
- 4+4
Dans les exercices suivants, simplifiez chaque expression.
10− (−19)
- Réponse
-
29
11− (−18)
31−79
- Réponse
-
−48
39−81
−31−11
- Réponse
-
−42
−32−18
−15− (−28) +5
- Réponse
-
18
71+ (−10) −8
−16− (−4+1) −7
- Réponse
-
-20
−15− (−6+4) −3
Multipliez des entiers
Dans les exercices suivants, multipliez.
−5 (7)
- Réponse
-
−35
−8 (6)
−18 (−2)
- Réponse
-
36
−10 (−6)
Diviser les entiers
Dans les exercices suivants, divisez.
\(-28 \div 7\)
- Réponse
-
-4
\(56 \div(-7)\)
\(-120 \div(-20)\)
- Réponse
-
6
\(-200 \div 25\)
Simplifier les expressions avec des entiers
Dans les exercices suivants, simplifiez chaque expression.
−8 (−2) −3 (−9)
- Réponse
-
43
−7 (−4) −5 (−3)
\((-5)^{3}\)
- Réponse
-
−125
\((-4)^{3}\)
\(-4 \cdot 2 \cdot 11\)
- Réponse
-
−88
\(-5 \cdot 3 \cdot 10\)
\(-10(-4) \div(-8)\)
- Réponse
-
-5
\(-8(-6) \div(-4)\)
31−4 (3−9)
- Réponse
-
55
24−3 (2−10)
Evaluer des expressions variables avec des entiers
Dans les exercices suivants, évaluez chaque expression.
x+8 quand
- x=−26
- x=−95
- Réponse
-
- −18
- −87
y+9 lorsque
- y=−29
- y=−84
Lorsque b=−11, évaluez :
- b+6
- −b+6
- Réponse
-
- −5
- 17
Lorsque c=−9, évaluez :
- c+ (−4) c+ (−4)
- −c+ (−4)
\(p^{2}-5 p+2\)quand
\(p=-1\)
- Réponse
-
8
\(q^{2}-2 q+9\)quand\(q=-2\)
\(6 x-5 y+15\)quand\(x=3\) et\(y=-1\)
- Réponse
-
38
\(3 p-2 q+9\)quand\(p=8\) et\(q=-2\)
Traduire des phrases anglaises en expressions algébriques
Dans les exercices suivants, traduisez en une expression algébrique et simplifiez si possible.
la somme de −4 et −17, augmentée de 32
- Réponse
-
(−4+ (−17)) +32 ; 11
- la différence de 15 et −7
- soustraire 15 de −7
le quotient de −45 et −9
- Réponse
-
\(\frac{-45}{-9} ; 5\)
le produit de -12 et la différence de c et d
Utiliser des nombres entiers dans les applications
Dans les exercices suivants, résolvez.
Température La température maximale d'un jour à Miami Beach, en Floride, était de 76°. Le même jour, la température maximale à Buffalo, dans l'État de New York, était de −8°. Quelle était la différence entre la température à Miami Beach et la température à Buffalo ?
- Réponse
-
84 degrés
Compte courant Adrianne a un solde de −22 $ sur son compte courant. Elle dépose 301$ sur le compte. Qu'est-ce que le nouvel équilibre ?
Visualisez les fractions
Trouver des fractions équivalentes
Dans les exercices suivants, trouvez trois fractions équivalentes à la fraction donnée. Montrez votre travail en utilisant des chiffres ou de l'algèbre.
\(\frac{1}{4}\)
- Réponse
-
\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\)les réponses peuvent varier
\(\frac{1}{3}\)
\(\frac{5}{6}\)
- Réponse
-
\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\)les réponses peuvent varier
\(\frac{2}{7}\)
Simplifier les
Dans les exercices suivants, simplifiez.
\(\frac{7}{21}\)
- Réponse
-
\(\frac{1}{3}\)
\(\frac{8}{24}\)
\(\frac{15}{20}\)
- Réponse
-
\(\frac{3}{4}\)
\(\frac{12}{18}\)
\(-\frac{168}{192}\)
- Réponse
-
\(-\frac{7}{8}\)
\(-\frac{140}{224}\)
\(\frac{11 x}{11 y}\)
- Réponse
-
\(\frac{x}{y}\)
\(\frac{15 a}{15 b}\)
Multiplier les fractions
Dans les exercices suivants, multipliez.
\(\frac{2}{5} \cdot \frac{1}{3}\)
- Réponse
-
\(\frac{2}{15}\)
\(\frac{1}{2} \cdot \frac{3}{8}\)
\(\frac{7}{12}\left(-\frac{8}{21}\right)\)
- Réponse
-
\(-\frac{2}{9}\)
\(\frac{5}{12}\left(-\frac{8}{15}\right)\)
\(-28 p\left(-\frac{1}{4}\right)\)
- Réponse
-
7p
\(-51 q\left(-\frac{1}{3}\right)\)
\(\frac{14}{5}(-15)\)
- Réponse
-
−42
\(-1\left(-\frac{3}{8}\right)\)
Diviser les fractions
Dans les exercices suivants, divisez
\(\frac{1}{2} \div \frac{1}{4}\)
- Réponse
-
2
\(\frac{1}{2} \div \frac{1}{8}\)
\(-\frac{4}{5} \div \frac{4}{7}\)
- Réponse
-
\(-\frac{7}{5}\)
\(-\frac{3}{4} \div \frac{3}{5}\)
\(\frac{5}{8} \div \frac{a}{10}\)
- Réponse
-
\(\frac{25}{4 a}\)
\(\frac{5}{6} \div \frac{c}{15}\)
\(\frac{7 p}{12} \div \frac{21 p}{8}\)
- Réponse
-
\(\frac{2}{9}\)
\(\frac{5 q}{12} \div \frac{15 q}{8}\)
\(\frac{2}{5} \div(-10)\)
- Réponse
-
\(-\frac{1}{25}\)
\(-18 \div-\left(\frac{9}{2}\right)\)
Dans les exercices suivants, simplifiez.
\(\frac{\frac{2}{3}}{\frac{8}{9}}\)
- Réponse
-
\(\frac{3}{4}\)
\(\frac{\frac{4}{5}}{\frac{8}{15}}\)
\(\frac{-\frac{9}{10}}{3}\)
- Réponse
-
\(-\frac{3}{10}\)
\(\frac{2}{\frac{5}{8}}\)
\(\frac{\frac{r}{5}}{\frac{s}{3}}\)
- Réponse
-
\(\frac{3 r}{5 s}\)
\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)
Simplifier les expressions écrites avec une barre de fraction
Dans les exercices suivants, simplifiez.
\(\frac{4+11}{8}\)
- Réponse
-
\(\frac{15}{8}\)
\(\frac{9+3}{7}\)
\(\frac{30}{7-12}\)
- Réponse
-
-6
\(\frac{15}{4-9}\)
\(\frac{22-14}{19-13}\)
- Réponse
-
\(\frac{4}{3}\)
\(\frac{15+9}{18+12}\)
\(\frac{5 \cdot 8}{-10}\)
- Réponse
-
-4
\(\frac{3 \cdot 4}{-24}\)
\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)
- Réponse
-
\(\frac{5}{2}\)
\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)
\(\frac{2+4(3)}{-3-2^{2}}\)
- Réponse
-
-2
\(\frac{7+3(5)}{-2-3^{2}}\)
Traduisez des phrases en expressions avec des fractions
Dans les exercices suivants, traduisez chaque phrase anglaise en une expression algébrique.
le quotient de c et la somme de d et 9.
- Réponse
-
\(\frac{c}{d+9}\)
le quotient de la différence entre h et k, et -5.
Ajouter et soustraire des fractions
Additionner et soustraire des fractions avec un dénominateur commun
Dans les exercices suivants, ajoutez.
\(\frac{4}{9}+\frac{1}{9}\)
- Réponse
-
\(\frac{5}{9}\)
\(\frac{2}{9}+\frac{5}{9}\)
\(\frac{y}{3}+\frac{2}{3}\)
- Réponse
-
\(\frac{y+2}{3}\)
\(\frac{7}{p}+\frac{9}{p}\)
\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)
- Réponse
-
\(-\frac{1}{2}\)
\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)
Dans les exercices suivants, soustrayez.
\(\frac{4}{5}-\frac{1}{5}\)
- Réponse
-
\(\frac{3}{5}\)
\(\frac{4}{5}-\frac{3}{5}\)
\(\frac{y}{17}-\frac{9}{17}\)
- Réponse
-
\(\frac{y-9}{17}\)
\(\frac{x}{19}-\frac{8}{19}\)
\(-\frac{8}{d}-\frac{3}{d}\)
- Réponse
-
\(-\frac{11}{d}\)
\(-\frac{7}{c}-\frac{7}{c}\)
Ajouter ou soustraire des fractions avec différents dénominateurs
Dans les exercices suivants, ajoutez ou soustrayez.
\(\frac{1}{3}+\frac{1}{5}\)
- Réponse
-
\(\frac{8}{15}\)
\(\frac{1}{4}+\frac{1}{5}\)
\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)
- Réponse
-
\(\frac{3}{10}\)
\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)
\(\frac{2}{3}+\frac{3}{4}\)
- Réponse
-
\(\frac{17}{12}\)
\(\frac{3}{4}+\frac{2}{5}\)
\(\frac{11}{12}-\frac{3}{8}\)
- Réponse
-
\(\frac{13}{24}\)
\(\frac{5}{8}-\frac{7}{12}\)
\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)
- Réponse
-
\(\frac{19}{80}\)
\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)
\(1+\frac{5}{6}\)
- Réponse
-
\(\frac{11}{6}\)
\(1-\frac{5}{9}\)
Utiliser l'ordre des opérations pour simplifier les fractions complexes
Dans les exercices suivants, simplifiez.
\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)
- Réponse
-
\(\frac{1}{275}\)
\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)
\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)
- Réponse
-
14
\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)
Évaluer des expressions variables avec des fractions
Dans les exercices suivants, évaluez.
\(x+\frac{1}{2}\)quand
- \(x=-\frac{1}{8}\)
- \(x=-\frac{1}{2}\)
- Réponse
-
- \(\frac{3}{8}\)
- \(0\)
\(x+\frac{2}{3}\)quand
- \(x=-\frac{1}{6}\)
- \(x=-\frac{5}{3}\)
4\(p^{2} q\) quand\(p=-\frac{1}{2}\) et\(q=\frac{5}{9}\)
- Réponse
-
\(\frac{5}{9}\)
5\(m^{2} n\) quand\(m=-\frac{2}{5}\) et\(n=\frac{1}{3}\)
\(\frac{u+v}{w}\)quand
\(u=-4, v=-8, w=2\)
- Réponse
-
-6
\(\frac{m+n}{p}\)quand
\(m=-6, n=-2, p=4\)
Décimales
Nommez et écrivez des décimales
Dans les exercices suivants, écrivez sous forme décimale.
Huit et trois centièmes
- Réponse
-
8.03
Neuf et sept centièmes
Un millième
- Réponse
-
0,001
Neuf millièmes
Dans les exercices suivants, nommez chaque décimale.
7,8
- Réponse
-
sept et huit dixièmes
5.01
0,005
- Réponse
-
cinq millièmes
0,381
Décimales rondes
Dans les exercices suivants, arrondissez chaque chiffre au plus proche
- centième
- dixième
- nombre entier.
5.7932
- Réponse
-
- 5,79
- 5,8
- 6
3.6 284
12.4768
- Réponse
-
- 12,48
- 12,5
- 12
25.8449
Ajouter et soustraire des décimales
Dans les exercices suivants, ajoutez ou soustrayez.
18,37+9,36
- Réponse
-
27,73
256,37 − 85,49
15,35−20,88
- Réponse
-
−5,53
37,5+12,23
−4,2 et 2 (−9,3)
- Réponse
-
−13,5
−8,6+ (−8,6)
100−64,2
- Réponse
-
35,8
100−65,83
2,51+40
- Réponse
-
42,51
9,38+60
Multipliez et divisez les décimales
Dans les exercices suivants, multipliez.
(0,3) (0,4)
- Réponse
-
0,12
(0,6) (0,7)
(8,52) (3,14)
- Réponse
-
26 75,28
(5,32) (4,86)
(0,09) (24,78)
- Réponse
-
2.2 302
(0,04) (36,89)
Dans les exercices suivants, divisez.
\(0.15 \div 5\)
- Réponse
-
0,03
\(0.27 \div 3\)
\(\$ 8.49 \div 12\)
- Réponse
-
0,71$
\(\$ 16.99 \div 9\)
\(12 \div 0.08\)
- Réponse
-
150
\(5 \div 0.04\)
Convertir des nombres décimaux, des fractions et des pourcentages
Dans les exercices suivants, écrivez chaque décimale sous forme de fraction.
0,08
- Réponse
-
\(\frac{2}{25}\)
0,17
0,425
- Réponse
-
\(\frac{17}{40}\)
0,184
1,75
- Réponse
-
\(\frac{7}{4}\)
0,035
Dans les exercices suivants, convertissez chaque fraction en décimale.
\(\frac{2}{5}\)
- Réponse
-
0,4
\(\frac{4}{5}\)
\(-\frac{3}{8}\)
- Réponse
-
−0,375
\(-\frac{5}{8}\)
\(\frac{5}{9}\)
- Réponse
-
\(0 . \overline{5}\)
\(\frac{2}{9}\)
\(\frac{1}{2}+6.5\)
- Réponse
-
7
\(\frac{1}{4}+10.75\)
Dans les exercices suivants, convertissez chaque pourcentage en décimal.
5 %
- Réponse
-
0,05
9 %
40 %
- Réponse
-
0,4
50 %
115 %
- Réponse
-
1,15
125 %
Dans les exercices suivants, convertissez chaque décimale en pourcentage.
0,18
- Réponse
-
18 %
0,15
0,009
- Réponse
-
0,9 %
0,008
1,5
- Réponse
-
150 %
2.2
Les vrais chiffres
Simplifiez les expressions avec des racines
Dans les exercices suivants, simplifiez.
\(\sqrt{64}\)
- Réponse
-
8
\(\sqrt{144}\)
\(-\sqrt{25}\)
- Réponse
-
-5
\(-\sqrt{81}\)
Identifier les entiers, les nombres rationnels, les nombres irrationnels et les nombres réels
Dans les exercices suivants, écrivez le ratio de deux nombres entiers.
- 9
- 8,47
- Réponse
-
- \(\frac{9}{1}\)
- \(\frac{847}{100}\)
- −15
- 3 591
Dans les exercices suivants, dressez la liste des
- nombres rationnels,
- nombres irrationnels.
\(0.84,0.79132 \ldots, 1 . \overline{3}\)
- Réponse
-
- \(0.84,1.3\)
- \(0.79132 \ldots\)
\(2.3 \overline{8}, 0.572,4.93814 \ldots\)
Dans les exercices suivants, déterminez si chaque nombre est rationnel ou irrationnel.
- \(\sqrt{121}\)
- \(\sqrt{48}\)
- Réponse
-
- rationnel
- irrationnel
- \(\sqrt{56}\)
- \(\sqrt{16}\)
Dans les exercices suivants, déterminez si chaque nombre est un nombre réel ou non.
- \(\sqrt{-9}\)
- \(-\sqrt{169}\)
- Réponse
-
- pas un vrai chiffre
- nombre réel
- \(\sqrt{-64}\)
- \(-\sqrt{81}\)
Dans les exercices suivants, dressez la liste des
- nombres entiers,
- entiers,
- nombres rationnels,
- nombres irrationnels,
- des nombres réels pour chaque série de nombres.
\(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
- Réponse
-
- \(0, \sqrt{16}\)
- \(-4,0, \sqrt{16}\)
- \(-4,0, \frac{5}{6}, \sqrt{16}\)
- \(\sqrt{18}, 5.2537 \ldots\)
- \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)
Localiser les fractions sur la droite numérique
Dans les exercices suivants, repérez les chiffres sur une ligne numérique.
\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)
- Réponse
-
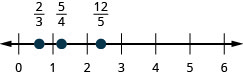
\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)
\(2 \frac{1}{3},-2 \frac{1}{3}\)
- Réponse
-
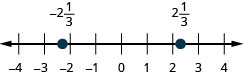
\(1 \frac{3}{5},-1 \frac{3}{5}\)
Dans les exercices suivants, ordonnez chacune des paires de nombres suivantes en utilisant < or >.
−1___\(-\frac{1}{8}\)
- Réponse
-
<
\(-3 \frac{1}{4}\)___−4
\(-\frac{7}{9}\)___\(\frac{4}{9}\)
- Réponse
-
>
\(-2\)___\(\frac{19}{8}\)
Localiser les décimales sur la ligne numérique
Dans les exercices suivants, trouvez la position sur la ligne numérique.
0,3
- Réponse
-
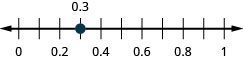
−0,2
−2,5
- Réponse
-
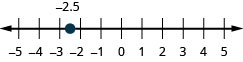
2.7
Dans les exercices suivants, ordonnez chacune des paires de nombres suivantes en utilisant < or >.
0,9___0,6
- Réponse
-
>
0,7___0,8
−0,6___−0,59
- Réponse
-
>
−0,27___−0,3
Propriétés des nombres réels
Utiliser les propriétés commutatives et associatives
Dans les exercices suivants, utilisez la propriété associative pour simplifier.
−12 (4 m)
- Réponse
-
−48 m
30\(\left(\frac{5}{6} q\right)\)
(+16) +31
- Réponse
-
a+47
(c+0,2) +0,7
Dans les exercices suivants, simplifiez.
6 ans+37 ans et plus (−6 ans)
- Réponse
-
37
\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)
\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)
- Réponse
-
\(\frac{35}{9}\)
\(-18 \cdot 15 \cdot \frac{2}{9}\)
\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)
- Réponse
-
1\(\frac{7}{12}\)
(3,98 d+0,75 d) +1,25 d
11 x 8 ans+16 x 15 ans
- Réponse
-
27 x 23 ans
Plus de 52 m (−20 n) + (−18 m) + (−5 n)
Utiliser l'identité et les propriétés inverses de l'addition et de la multiplication
Dans les exercices suivants, trouvez l'inverse additif de chaque nombre.
- \(\frac{1}{3}\)
- 5.1
- \(-14\)
- \(-\frac{8}{5}\)
- Réponse
-
- \(-\frac{1}{3}\)
- \(-5.1\)
- -14
- \(-\frac{8}{5}\)
- \(-\frac{7}{8}\)
- \(-0.03\)
- 17
- \(\frac{12}{5}\)
Dans les exercices suivants, trouvez l'inverse multiplicatif de chaque nombre.
- \(10\)
- \(-\frac{4}{9}\)
- 0,6
- Réponse
-
- \(\frac{1}{10}\)
- \(-\frac{9}{4}\)
- \(\frac{5}{3}\)
- \(-\frac{9}{2}\)
- -7
- 2.1
Utiliser les propriétés de zéro
Dans les exercices suivants, simplifiez.
83\(\cdot 0\)
- Réponse
-
0
\(\frac{0}{9}\)
\(\frac{5}{0}\)
- Réponse
-
indéfini
\(0 \div \frac{2}{3}\)
Dans les exercices suivants, simplifiez.
43+39+ (−43)
- Réponse
-
39
(n+6,75) +0,25
\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)
- Réponse
-
57
\(\frac{1}{6} \cdot 17 \cdot 12\)
\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)
- Réponse
-
8
\(9(6 x-11)+15\)
Simplifier les expressions en utilisant la propriété distributive
Dans les exercices suivants, simplifiez l'utilisation de la propriété distributive.
7 (x+9)
- Réponse
-
7 x 63
9 (u−4)
−3 (6 m−1)
- Réponse
-
−18 m+3
−8 (−7 a−12)
\(\frac{1}{3}(15 n-6)\)
- Réponse
-
5n−2
\((y+10) \cdot p\)
(a−4) − (6a+9)
- Réponse
-
−5a−13
4 (x+3) −8 (x−7)
Systèmes de mesure
1.1 Définir les unités de mesure américaines et les convertir d'une unité à l'autre
Dans les exercices suivants, convertissez les unités. Arrondir au dixième le plus proche.
Une tonnelle fleurie mesure 7 pieds de haut. Convertissez la hauteur en pouces.
- Réponse
-
84 pouces
Un cadre photo mesure 42 pouces de large. Convertissez la largeur en pieds.
Kelly mesure 5 pieds 4 pouces. Convertissez sa taille en pouces.
- Réponse
-
64 pouces
Une aire de jeux mesure 45 pieds de large. Convertissez la largeur en mètres.
La hauteur du mont Shasta est de 14 179 pieds. Convertissez la hauteur en miles.
- Réponse
-
2,7 milles
Shamu pèse 4,5 tonnes. Convertissez le poids en livres.
La pièce a duré des\(1\frac{3}{4}\) heures. Convertissez le temps en minutes.
- Réponse
-
105 minutes
Combien de cuillères à soupe y a-t-il dans une pinte ?
Le bébé de Naomi pesait 5 livres 14 onces à la naissance. Convertissez le poids en onces.
- Réponse
-
94 onces
Trinh a besoin de 30 tasses de peinture pour son projet artistique en classe. Convertissez le volume en gallons.
Utilisez des unités de mesure mixtes dans le système américain.
Dans les exercices suivants, résolvez.
John a attrapé 4 homards. Le poids des homards était de 1 livre 9 onces, 1 livre 12 onces, 4 livres 2 onces et 2 livres 15 onces. Quel était le poids total des homards ?
- Réponse
-
10 livres 6 oz
Chaque jour de la semaine dernière, Pedro a enregistré le nombre de minutes qu'il a passées à lire. Le nombre de minutes était de 50, 25, 83, 45, 32, 60, 135. Combien d'heures Pedro a-t-il passées à lire ?
Fouad mesure 6 pieds 2 pouces. S'il se tient debout sur un échelon d'une échelle de 8 pieds 10 pouces de haut, à quelle hauteur du sol se trouve le sommet de la tête de Fouad ?
- Réponse
-
15 pieds
Dalila veut fabriquer des housses de coussin. Chaque housse prend 30 pouces de tissu. De combien de mètres de tissu a-t-elle besoin pour 4 housses ?
Procéder à des conversions d'unités dans le système métrique
Dans les exercices suivants, convertissez les unités.
Donna mesure 1,7 mètre. Convertissez sa taille en centimètres.
- Réponse
-
170 centimètres
Le mont Everest s'élève à 8 850 mètres. Convertissez la hauteur en kilomètres.
Une tasse de yogourt contient 488 milligrammes de calcium. Convertissez-le en grammes.
- Réponse
-
0,488 grammes
Une tasse de yogourt contient 13 grammes de protéines. Convertissez-le en milligrammes.
Sergio pesait 2,9 kilogrammes à la naissance. Convertissez-le en grammes.
- Réponse
-
2 900 grammes
Une bouteille d'eau contenait 650 millilitres. Convertissez-le en litres.
Utiliser des unités de mesure mixtes dans le système métrique
Dans les exercices suivants, résolvez.
Minh mesure 2 mètres de haut. Sa fille mesure 88 centimètres. Minh est-il plus grand que sa fille ?
- Réponse
-
1,12 mètre
Selma avait une bouteille d'eau d'un litre. Si elle a bu 145 millilitres, combien d'eau restait-il dans la bouteille ?
Une portion de jus de canneberge contient 30 grammes de sucre. Combien de kilogrammes de sucre contiennent 30 portions de jus de canneberge ?
- Réponse
-
0,9 kilogrammes
Une once de tofu a fourni 2 grammes de protéines. Combien de milligrammes de protéines sont fournis par 5 onces de tofu ?
Convertir entre les États-Unis et les systèmes de mesure métriques
Dans les exercices suivants, effectuez les conversions d'unités. Arrondir au dixième le plus proche.
Majid mesure 69 pouces. Convertissez sa taille en centimètres.
- Réponse
-
175,3 centimètres
Un terrain de basket universitaire mesure 84 pieds de long. Convertissez cette longueur en mètres.
Caroline a marché 2,5 kilomètres. Convertissez cette longueur en miles.
- Réponse
-
1,6 milles
Lucas pèse 78 kilogrammes. Convertissez son poids en livres.
La voiture de Steve contient 55 litres d'essence. Convertissez-le en gallons.
- Réponse
-
14,6 gallons
Une boîte de livres pèse 25 livres. Convertissez le poids en kilogrammes.
Convertir entre les températures Fahrenheit et Celsius
Dans les exercices suivants, convertissez les températures en degrés Fahrenheit en degrés Celsius. Arrondir au dixième le plus proche.
95° Fahrenheit
- Réponse
-
35 °C
23° Fahrenheit
20° Fahrenheit
- Réponse
-
—6,7 °C
64° Fahrenheit
Dans les exercices suivants, convertissez les températures Celsius en degrés Fahrenheit. Arrondir au dixième le plus proche.
30 degrés Celsius
- Réponse
-
86° F
—5° Celsius
—12 degrés Celsius
- Réponse
-
10,4 °F
24 degrés Celsius
Chapitre : Test pratique
Écrivez un nombre entier en utilisant des chiffres : deux cent cinq mille, six cent dix-sept.
- Réponse
-
205 617
Trouvez la factorisation première de 504.
Détermine le multiple le moins courant de 18 et 24.
- Réponse
-
72
Combinez des termes similaires : 5n+8+2n−1.
Dans les exercices suivants, évaluez.
\(-|x|\)quand\(x=-2\)
- Réponse
-
−2
11−a lorsque a=−3
Traduisez en une expression algébrique et simplifiez : vingt de moins que moins 7.
- Réponse
-
−7−20 ; −27
Monique a un solde de −18 $ sur son compte courant. Elle dépose 152$ sur le compte. Qu'est-ce que le nouvel équilibre ?
Arrondissez 677,1348 au centième le plus proche.
- Réponse
-
677,13
Convertit\(\frac{4}{5}\) en décimal.
Convertissez 1,85 en pourcentage.
- Réponse
-
185 %
Localisez\(\frac{2}{3},-1.5,\) et\(\frac{9}{4}\) sur une ligne numérique.
Dans les exercices suivants, simplifiez chaque expression.
\(4+10(3+9)-5^{2}\)
- Réponse
-
99
−85+42
−19−25
- Réponse
-
−44
\((-2)^{4}\)
\(-5(-9) \div 15\)
- Réponse
-
3
\(\frac{3}{8} \cdot \frac{11}{12}\)
\(\frac{4}{5} \div \frac{9}{20}\)
- Réponse
-
\(\frac{16}{9}\)
\(\frac{12+3 \cdot 5}{15-6}\)
\(\frac{m}{7}+\frac{10}{7}\)
- Réponse
-
\(\frac{m+10}{7}\)
\(\frac{7}{12}-\frac{3}{8}\)
\(-5.8+(-4.7)\)
- Réponse
-
−10,5
100−64,25
(0,07) (31,95)
- Réponse
-
2.2365
\(9 \div 0.05\)
\(-14\left(\frac{5}{7} p\right)\)
- Réponse
-
−10 p
(u+8) −9
6x+ (−4 ans) +9 x+8 ans
- Réponse
-
15 x +4 ans
\(\frac{0}{23}\)
\(\frac{75}{0}\)
- Réponse
-
indéfini
−2 (13 q−5)
Un film a duré 1\(\frac{2}{3}\) heure. Combien de minutes cela a-t-il duré ? (1 heure et\(=60\) minutes)
- Réponse
-
100 minutes
Le VUS de Mike mesure 5 pieds 11 pouces de haut. Il veut mettre un sac de chargement sur le toit du SUV. Le sac de chargement mesure 1 pied 6 pouces de haut. Quelle sera la hauteur totale du VUS avec le sac de chargement sur le toit ? (1 pied = 12 pouces)
Jennifer a couru 4,5 km. Convertissez cette longueur en kilomètres. (1 mile = 1,61 kilomètres)
- Réponse
-
4 508 km


