1.11 : Systèmes de mesure
- Page ID
- 195331
À la fin de cette section, vous serez en mesure de :
- Procéder à des conversions d'unités dans le système américain
- Utiliser des unités de mesure mixtes dans le système américain
- Procéder à des conversions d'unités dans le système métrique
- Utiliser des unités de mesure mixtes dans le système métrique
- Convertir entre le système de mesure américain et le système de mesure métrique
- Convertir entre les températures Fahrenheit et Celsius
Une introduction plus complète aux sujets abordés dans cette section se trouve dans le chapitre sur la préalgèbre, Les propriétés des nombres réels.
Procéder à des conversions d'unités dans le système américain
Il existe deux systèmes de mesure couramment utilisés dans le monde. La plupart des pays utilisent le système métrique. Les États-Unis utilisent un système de mesure différent, généralement appelé système américain. Nous allons d'abord examiner le système américain.
Le système de mesure américain utilise les unités de pouce, de pied, de verge et de mile pour mesurer la longueur et la livre et la tonne pour mesurer le poids. Pour la capacité, les unités utilisées sont la tasse, la pinte, la pinte et les gallons. Le système américain et le système métrique mesurent le temps en secondes, minutes et heures.
Les équivalences des mesures sont présentées dans le tableau\(\PageIndex{1}\). Le tableau indique également, entre parenthèses, les abréviations courantes pour chaque mesure.
| Système de mesure américain | |
|---|---|
| \(\begin{array} {llll} {} &{\text{1 foot (ft.)}} &{=} &{\text{12 inches (in.)}} \\ {\textbf{Length}} &{\text{1 yard (yd.)}} &{=} &{\text{3 feet (ft.)}} \\ {} &{\text{1 mile (mi.)}} &{=} &{\text{5280 feet (ft.)}} \end{array}\) | \(\begin{array} {llll} {} &{\text{3 teaspoons (t)}} &{=} &{\text{1 tablespoon (T)}} \\ {} &{\text{16 tablespoons (T)}} &{=} &{\text{1 cup (C)}} \\ {} &{\text{1 cup (C)}} &{=} &{\text{8 fluid ounces (fl.oz.)}} \\ {\textbf{Volume}} &{\text{1 pint (pt.)}} &{=} &{\text{2 cups (C)}} \\ {} &{\text{1 quart (qt.)}} &{=} &{\text{2 pints (ft.)}} \\ {} &{\text{1 gallon (gal)}} &{=} &{\text{4 quarts (qt.)}} \end{array}\) |
|
\(\begin{array} {llll} {\textbf{Weight}} &{\text{1 pound (lb.)}} &{=} &{\text{16 ounces (oz.)}} \\ {} &{\text{1 ton}} &{=} &{\text{2000 pounds (lb.)}} \end{array}\) |
\(\begin{array} {llll} {} &{\text{1 minute (min)}} &{=} &{\text{60 seconds (sec)}} \\ {} &{\text{1 hour (hr)}} &{=} &{\text{60 minutes (min)}} \\ {\textbf{Time}} &{\text{1 day}} &{=} &{\text{24 hours (hr)}} \\ {} &{\text{1 week (wk)}} &{=} &{\text{7 days}} \\ {} &{\text{1 year (yr)}} &{=} &{\text{365 days}} \end{array}\) |
Dans de nombreuses applications réelles, nous devons effectuer des conversions entre des unités de mesure, telles que les pieds et les yards, les minutes et les secondes, les quarts et les gallons, etc. Nous utiliserons la propriété d'identité de multiplication pour effectuer ces conversions. Nous allons reformuler la propriété identitaire de la multiplication ici pour en faciliter la consultation.
\(\begin{array} { l l } { \text {For any real number } a : } & { a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1} \text { is the } \textbf{multiplicative identity } } \end{array}\)
Pour utiliser la propriété d'identité de la multiplication, nous écrivons 1 sous une forme qui nous aidera à convertir les unités. Supposons, par exemple, que nous souhaitions remplacer les pouces par les pieds. Nous savons que 1 pied est égal à 12 pouces, nous allons donc écrire 1 comme fraction\(\frac{\text{1 foot}}{\text{12 inches}}\). Lorsque nous multiplions par cette fraction, nous ne changeons pas la valeur, mais simplement les unités.
Mais est\(\frac{\text{12 inches}}{\text{1 foot}}\) également égal à 1. Comment décide-t-on de multiplier par\(\frac{\text{1 foot}}{\text{12 inches}}\) ou par\(\frac{\text{12 inches}}{\text{1 foot}}\) ? Nous choisissons la fraction qui divisera les unités que nous voulons convertir. Traitez les mots unitaires comme des facteurs et « divisez » les unités communes comme nous le faisons pour les facteurs communs. Si nous voulons convertir 6666 pouces en pieds, quelle multiplication éliminera les pouces ?

Les pouces se séparent et ne laissent que des pieds. Le deuxième formulaire ne comporte aucune unité qui se divise et ne nous aidera donc pas.
Mary Anne mesure 66 pouces. Convertit sa taille en pieds.
- Réponse
-




Lexie mesure 30 pouces. Convertit sa taille en pieds.
- Réponse
-
2,5 pieds
René a acheté un tuyau de 18 mètres de long. Convertissez la longueur en pieds.
- Réponse
-
54 pieds
- Multipliez la mesure à convertir par 1 ; écrivez 1 sous forme de fraction reliant les unités données et les unités nécessaires.
- Multipliez.
- Simplifiez la fraction.
- Simplifiez.
Lorsque nous utilisons la propriété d'identité de la multiplication pour convertir des unités, nous devons nous assurer que les unités à partir desquelles nous voulons changer se diviseront. Cela signifie généralement que nous voulons que la fraction de conversion ait ces unités dans le dénominateur.
Ndula, un éléphant du parc safari de San Diego, pèse près de 3,2 tonnes. Convertissez son poids en livres.
- Réponse
-
Nous allons convertir 3,2 tonnes en livres. Nous utiliserons la propriété d'identité de la multiplication, en écrivant 1 comme fraction\(\frac{\text{2000 pounds}}{\text{1 ton}}\).
\(\text{3.2 tons}\) Multipliez la mesure à convertir par 1. \(\text{3.2 tons} \cdot 1\) Écrivez 1 comme une fraction relative aux tonnes et aux livres. \(\text{3.2 tons} \cdot \frac{\text{2000 pounds}}{\text{1 ton}}\) Simplifiez. 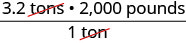
Multipliez. 6400 livres Ndula pèse près de 6400 livres.
Le SUV d'Arnold pèse environ 4,3 tonnes. Convertissez le poids en livres.
- Réponse
-
8600 livres
Le bateau de croisière Carnival Destiny pèse 51 000 tonnes. Convertissez le poids en livres.
- Réponse
-
102 000 000 livres
Parfois, pour passer d'une unité à une autre, il se peut que nous devions utiliser plusieurs autres unités entre les deux. Nous devrons donc multiplier plusieurs fractions.
Juliet part avec sa famille dans leur résidence d'été. Elle sera éloignée de son petit ami pendant 9 semaines. Convertissez le temps en minutes.
- Réponse
-
Pour convertir les semaines en minutes, nous convertirons les semaines en jours, les jours en heures, puis les heures en minutes. Pour ce faire, nous allons multiplier par des facteurs de conversion de 1.
9 semaines Ecrivez 1 en tant que\(\frac{\text{7 days}}{\text{1 week}}\), et\(\frac{\text{60 minutes}}{\text{1 hour}}\). \(\frac{\text{9 wk}}{\text{1}}\cdot\frac{\text{7 days}}{\text{1 wk}}\cdot\frac{\text{24 hr}}{\text{1 day}}\cdot\frac{\text{60 min}}{\text{1 hr}}\) Répartissez les unités communes. 
Multipliez. \(\frac{9\cdot7\cdot24\cdot60\text{ min}}{1\cdot1\cdot1\cdot1}\) Multipliez. 90 720 minutes Juliette et son petit ami seront séparés pendant 90 720 minutes (même si cela peut sembler une éternité !).
La distance entre la Terre et la Lune est d'environ 250 000 miles. Convertissez cette longueur en mètres.
- Réponse
-
440 000 000 mètres
Les astronautes de l'Expédition 28 à bord de la Station spatiale internationale passent 15 semaines dans l'espace. Convertissez le temps en minutes.
- Réponse
-
151 200 minutes
Combien d'onces y a-t-il dans 1 gallon ?
- Réponse
-
Nous convertirons les gallons en onces en multipliant par plusieurs facteurs de conversion. Reportez-vous au tableau\(\PageIndex{1}\).
1 gallon Multipliez la mesure à convertir par 1. \(\frac{\text{1 gallon}}{\text{1}} \cdot \frac{\text{4 quarts}}{\text{1 gallon}} \cdot \frac{\text{2 pints}}{\text{1 quart}} \cdot \frac{\text{2 cups}}{\text{1 pint}} \cdot \frac{\text{8 ounces}}{\text{1 cup}}\) Utilisez des facteurs de conversion pour obtenir la bonne unité.
Simplifiez.
Multipliez. \(\frac{1\cdot 4\cdot 2\cdot 2\cdot 8\text{ ounces}}{1\cdot 1\cdot 1\cdot 1\cdot 1 }\) Simplifiez. 128 onces
Combien de tasses y a-t-il dans 1 gallon ?
- Réponse
-
16 tasses
Combien de cuillères à café y a-t-il dans une tasse ?
- Réponse
-
48 cuillères à café
Utiliser des unités de mesure mixtes dans le système américain
Nous utilisons souvent des unités de mesure mixtes dans des situations de tous les jours. Supposons que Joe mesure 5 pieds 10 pouces, reste au travail pendant 7 heures et 45 minutes, puis mange un steak de 1 livre 2 onces pour le dîner. Toutes ces mesures ont des unités mixtes.
L'exécution d'opérations arithmétiques sur des mesures avec des unités de mesure mixtes nécessite de la prudence. Assurez-vous d'ajouter ou de soustraire des unités similaires !
Seymour a acheté trois steaks pour un barbecue. Leur poids était de 14 onces, 1 livre 2 onces et 1 livre 6 onces. Combien de kilos de steak a-t-il achetés au total ?
- Réponse
-
Nous ajouterons les poids des steaks pour obtenir le poids total des steaks.
Ajoutez les onces. Ajoutez ensuite les kilos. 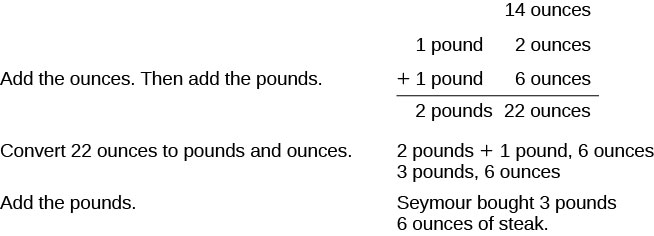
Convertissez 22 onces en livres et onces. 2 livres+1 livre, 6 onces Ajoutez les kilos. 3 livres, 6 onces Seymour a acheté 3 livres 6 onces de steak.
Laura a donné naissance à des triplés pesant 3 livres 3 onces, 3 livres 3 onces et 2 livres 9 onces. Quel était le poids total à la naissance des trois bébés ?
- Réponse
-
8 livres 15 onces
Stan a découpé deux pièces de moulures couronnées pour sa chambre familiale qui mesuraient 8 pieds 7 pouces et 12 pieds 11 pouces. Quelle était la longueur totale de la moulure ?
- Réponse
-
21 pieds 6 pouces
Anthony a acheté quatre planches de bois de 6 pieds 4 pouces de long chacune. Quelle est la longueur totale du bois qu'il a acheté ?
- Réponse
-
Nous allons multiplier la longueur d'une planche pour obtenir la longueur totale.
Multipliez les pouces puis les pieds. 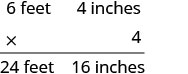
Convertissez les 16 pouces en pieds.
Ajoutez les pieds.
Anthony a acheté 25 pieds et 4 pouces de bois.
Henri veut tripler sa recette de sauce à spaghetti qui utilise 1 livre 8 onces de dinde hachée. De combien de kilos de dinde hachée aura-t-il besoin ?
- Réponse
-
4 livres 8 oz
Joellen veut doubler une solution de 5 gallons 3 pintes. Combien de gallons de solution aura-t-elle en tout ?
- Réponse
-
11 gallons 2 pintes
Procéder à des conversions d'unités dans le système métrique
Dans le système métrique, les unités sont reliées par des puissances de 10. Les mots de base de leurs noms reflètent cette relation. Par exemple, l'unité de base pour mesurer la longueur est le mètre. Un kilomètre est égal à 1 000 mètres ; le préfixe kilo signifie mille. Un centimètre correspond\(\frac{1}{100}\) à un mètre, tout comme un cent correspond\(\frac{1}{100}\) à un dollar.
Les équivalences des mesures dans le système métrique sont présentées dans le tableau\(\PageIndex{2}\). Les abréviations communes pour chaque mesure sont indiquées entre parenthèses.
| Système de mesure métrique | ||
|---|---|---|
| Longueur | Masse | Capacité |
| 1 kilomètre (km) = 1 000 m 1 hectomètre (hm) = 100 m 1 débamètre (barrage) = 10 m 1 mètre (m) = 1 m 1 décimètre (dm) = 0,1 m 1 centimètre (cm) = 0,01 m 1 millimètre (mm) = 0,001 m |
1 kilogramme (kg) = 1 000 g 1 hectogramme (hg) = 100 g 1 kilogramme (jour) = 10 g 1 gramme (g) = 1 g 1 décigramme (dg) = 0,1 g 1 centigramme (cg) = 0,01 g 1 milligramme (mg) = 0,001 g |
1 kilolitre (kL) = 1 000 L 1 hectolitre (hL) = 100 L 1 dékalitre (dAL) = 10 L 1 litre (L) = 1 L 1 décilitre (dL) = 0,1 L 1 centilitre (cL) = 0,01 L 1 millilitre (ml) = 0,001 L |
| 1 mètre = 100 centimètres 1 mètre = 1 000 millimètres |
1 gramme = 100 centigrammes 1 gramme = 1 000 milligrammes |
1 litre = 100 centilitres 1 litre = 1 000 millilitres |
Pour effectuer des conversions dans le système métrique, nous utiliserons la même technique que celle utilisée dans le système américain. En utilisant la propriété d'identité de la multiplication, nous allons multiplier par un facteur de conversion de un pour obtenir les unités correctes.
Avez-vous déjà couru une course de 5 km ou 10 km ? La durée de ces courses est mesurée en kilomètres. Le système métrique est couramment utilisé aux États-Unis pour parler de la durée d'une course.
Nick a couru une course de 10 km. Combien de mètres a-t-il parcouru ?
- Réponse
-
Nous convertirons les kilomètres en mètres en utilisant la propriété d'identité de multiplication.
10 kilomètres Multipliez la mesure à convertir par 1. 
Écrivez 1 sous forme de fraction relative aux kilomètres et aux mètres. 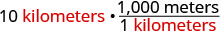
Simplifiez. 
Multipliez. 10 000 mètres Nick a couru 10 000 mètres.
Sandy a terminé sa première course de 5 km ! Combien de mètres a-t-elle couru ?
- Réponse
-
5 000 mètres
Herman a acheté un tapis de 2,5 mètres de long. Quelle est la longueur en centimètres ?
- Réponse
-
250 centimètres
Le nouveau-né d'Eleanor pesait 3 200 grammes. Combien de kilogrammes pesait le bébé ?
- Réponse
-
Nous allons convertir les grammes en kilogrammes.

Multipliez la mesure à convertir par 1. 
Écrivez 1 en tant que fonction reliant les kilogrammes et les grammes. 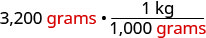
Simplifiez. 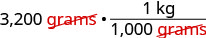
Multipliez. \(\frac{3,200 \text{ kilograms}}{1,000}\) Diviser. 3,2 kilogrammes
Le bébé pesait 3,2 kilogrammes.
Le nouveau-né de Kari pesait 2 800 grammes. Combien de kilogrammes pesait le bébé ?
- Réponse
-
2,8 kilogrammes
Anderson a reçu un colis marqué de 4 500 grammes. Combien de kilogrammes pesait ce colis ?
- Réponse
-
4,5 kilogrammes
Au fur et à mesure que vous vous familiariserez avec le système métrique, vous verrez peut-être une tendance. Comme le système est basé sur des multiples de dix, les calculs consistent à multiplier par des multiples de dix. Nous avons appris à simplifier ces calculs en déplaçant simplement la décimale.
Pour multiplier par 10, 100 ou 1 000, nous déplaçons la décimale vers la droite d'une, deux ou trois places, respectivement. Pour multiplier par 0,1, 0,01 ou 0,001, nous déplaçons la décimale vers la gauche d'une, deux ou trois places, respectivement.
Nous pouvons appliquer ce modèle lorsque nous effectuons des conversions de mesures dans le système métrique. Dans Exercice\(\PageIndex{25}\), nous avons changé 3 200 grammes en kilogrammes en multipliant par\(\frac{1}{1000}\) (ou 0,001). Cela revient à déplacer la décimale de trois décimales vers la gauche.
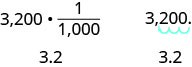
Convertir
- 350 L en kilolitres
- 4.1 L en millilitres.
- Réponse
-
1. Nous allons convertir les litres en kilolitres. Dans le tableau\(\PageIndex{2}\), nous voyons que 1 kilolitre = 1 000 litres.1 kilolitre = 1 000 litres.
350 L Multipliez par 1, en écrivant 1 comme une fraction reliant les litres aux kilolitres. \(350 \text{ L}\frac{\text{1 kL}}{\text{1000L}}\) Simplifiez. \(350 \not{\text{ L}}\frac{\text{1 kL}}{1000 \not\text{ L}}\) 
0,35 ml
2. Nous allons convertir les litres en millilitres. Dans le tableau,\(\PageIndex{2}\) nous voyons que 1 litre = 1 000 millilitres.1 litre = 1 000 millilitres.
Multipliez par 1, en écrivant 1 comme une fraction reliant les litres aux millilitres. 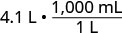
Simplifiez. 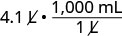
Déplace la décimale 3 unités vers la droite. 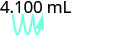

Convertir :
- 725 L en kilolitres
- 6.3 L en millilitres
- Réponse
-
- 7 250 kilomètres
- 6 300 millilitres
Convertir :
- 350 hL en litres
- 4.1 L en centilitres
- Réponse
-
- 35 000 litres
- 410 centilitres
Utiliser des unités de mesure mixtes dans le système métrique
L'exécution d'opérations arithmétiques sur des mesures avec des unités de mesure mixtes dans le système métrique nécessite le même soin que celui utilisé dans le système américain. Mais cela peut être plus facile en raison de la relation entre les unités et les puissances de 10. Assurez-vous d'ajouter ou de soustraire des unités similaires.
Ryland mesure 1,6 mètre de haut. Son frère cadet mesure 85 centimètres. Combien plus grand Ryland est-il plus grand que son frère cadet ?
- Réponse
-
Nous pouvons convertir les deux mesures en centimètres ou en mètres. Comme le mètre est l'unité la plus grande, nous soustrairons les longueurs en mètres. Nous convertissons 85 centimètres en mètres en déplaçant la décimale de 2 places vers la gauche.
\[\begin{array} { cc } { \text {Write the } 85 \text { centimeters as meters. } } & { 1.60 \mathrm { m } } \\ {} &{ \dfrac { - 0.85 \mathrm { m } } { 0.75 \mathrm { m } } } \end{array}\]
Ryland mesure 0,75 m (0,75 m) de plus que son frère.
Mariella mesure 1,58 mètre. Sa fille mesure 75 centimètres. Mariella est-elle plus grande que sa fille ? Écrivez la réponse en centimètres.
- Réponse
-
83 centimètres
La clôture qui entoure la cour de Hank mesure 2 mètres de haut. Hank mesure 96 centimètres. Combien de temps est plus court que la clôture, Hank ? Écrivez la réponse en mètres.
- Réponse
-
1,04 mètres
La recette de soupe aux lentilles de Dena nécessite 150 millilitres d'huile d'olive. Dena veut tripler la recette. De combien de litres d'huile d'olive aura-t-elle besoin ?
- Réponse
-
Nous trouverons la quantité d'huile d'olive en millilitres puis la convertirons en litres.
\(\begin{array} { ll } {} & { \text { Triple } 150 \text{ mL}} \\ { \text { Translate to algebra. } } &{3\cdot 150 \text{ mL}} \\ { \text { Multiply. } } &{450\text{ mL}}\\ { \text { Convert to liters. } } &{450\cdot \frac{0.001\text{ L}}{1 \text{ ml}}} \\ { \text { Simplify. } } &{0.45 \text{ L}}\\ {} &{ \text { Dena needs 0.45 liters of olive oil. } } \end{array}\)
Une recette de sauce Alfredo nécessite 250 millilitres de lait. Renata prépare des pâtes à la sauce Alfredo pour une grande fête et doit multiplier les quantités de la recette par 8. De combien de litres de lait aura-t-elle besoin ?
- Réponse
-
2 litres
Pour préparer une poêle de baklava, Dorothea a besoin de 400 grammes de pâte filo. Si Dorothea prévoit de préparer 6 moules de baklava, de combien de kilogrammes de pâte filo aura-t-elle besoin ?
- Réponse
-
2,4 kilogrammes
Convertir entre le système de mesure américain et le système de mesure métrique
Aux États-Unis, de nombreuses mesures sont effectuées en unités métriques. Notre soda peut se présenter dans des bouteilles de 2 litres, notre calcium peut se présenter sous forme de capsules de 500 mg et nous pouvons courir une course de 5 km. Pour travailler facilement dans les deux systèmes, nous devons pouvoir effectuer des conversions entre les deux systèmes.
Le\(\PageIndex{3}\) tableau présente certaines des conversions les plus courantes.
| Facteurs de conversion entre les systèmes américains et métriques | ||
|---|---|---|
| Longueur | Masse | Capacité |
| \(\begin{array} { l l l } {1 \text{ in.}} & {=} &{2.54 \text{ cm}} \\ {1\text{ ft.}} &{=} &{0.305 \text{ m}} \\ {1 \text{ yd.}} & {=} &{0.914 \text{ m}} \\ {1\text{ mi.}} &{=} &{1.61 \text{ km}} \\ {1 \text{ m}} & {=} &{3.28 \text{ ft}} \end{array}\) | \(\begin{array} { l l l } {1 \text{ lb.}} & {=} &{0.45 \text{ kg}} \\ {1\text{ oz.}} &{=} &{28 \text{ g}} \\ {1 \text{ kg}} & {=} &{2.2 \text{ lb}} \end{array}\) | \(\begin{array} { l l l } {1 \text{ qt.}} & {=} &{0.95 \text{ L}} \\ {1\text{ fl. oz.}} &{=} &{30 \text{ ml}} \\ {1 \text{ L}} & {=} &{1.06 \text{ lb}} \end{array}\) |
La figure\(\PageIndex{3}\) montre comment les pouces et les centimètres sont liés sur une règle.

La figure\(\PageIndex{4}\) montre les marques en onces et en millilitres sur une tasse à mesurer.
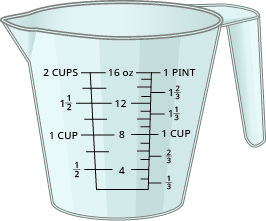
La figure\(\PageIndex{5}\) montre comment les livres et les kilogrammes sont marqués sur une balance de salle de bain.

Nous effectuons des conversions entre les systèmes comme nous le faisons au sein des systèmes, en les multipliant par des facteurs de conversion unitaires.
La bouteille d'eau Lee contient 500 ml d'eau. Combien y a-t-il d'onces dans la bouteille ? Arrondir au dixième d'once le plus proche.
- Réponse
-
\(\begin{array} { l l } {} & {500 \text{ mL}} \\ {\text{Multiplying by a unit conversion factor relating}} &{500\text{ milliliters}\cdot\frac{1\text{ ounce}}{30\text{ milliliters}}} \\ {\text{mL and ounces}} &{} \\ {\text{Simplify.}} &{\frac{50\text{ ounce}}{30}} \\ {\text{Divide.}} &{16.7\text{ ounces}} \\ {} &{\text{The water bottle has 16.7 ounces}} \end{array}\)
Combien de litres de soda se trouvent dans une bouteille de 2 L ?
- Réponse
-
2,12 pintes
Combien de litres y a-t-il dans 4 pintes de lait ?
- Réponse
-
3,8 litres
Soleil était en voyage et a vu un panneau indiquant que la prochaine aire de repos se trouvait dans 100 kilomètres. Combien de kilomètres jusqu'à la prochaine aire de repos ?
- Réponse
-
\(\begin{array} { l l } {} & {100 \text{ kilometers}} \\ {\text{Multiplying by a unit conversion factor relating}} &{100\text{ kilometers}\cdot\frac{1\text{ mile}}{1.61\text{ kilometers}}} \\ {\text{km and mi.}} &{} \\ {\text{Simplify.}} &{\frac{100\text{ miles}}{1.61}} \\ {\text{Divide.}} &{62\text{ miles}} \\ {} &{\text{Soleil will travel 62 miles.}} \end{array}\)
La hauteur du mont Kilimandjaro est de 5 895 mètres. Convertissez la hauteur en pieds.
- Réponse
-
19 335,6 pieds
La distance de vol entre New York City et Londres est de 5 586 kilomètres. Convertissez la distance en miles.
- Réponse
-
3 469,57 miles
Convertir entre les températures Fahrenheit et Celsius
Avez-vous déjà été dans un pays étranger et avez-vous entendu les prévisions météorologiques ? Si la prévision est de 22 °C, qu'est-ce que cela signifie ?
Les systèmes américains et métriques utilisent des échelles différentes pour mesurer la température. Le système américain utilise les degrés Fahrenheit, écrits °F. Le système métrique utilise les degrés Celsius, écrits °C. La figure\(\PageIndex{6}\) montre la relation entre les deux systèmes.
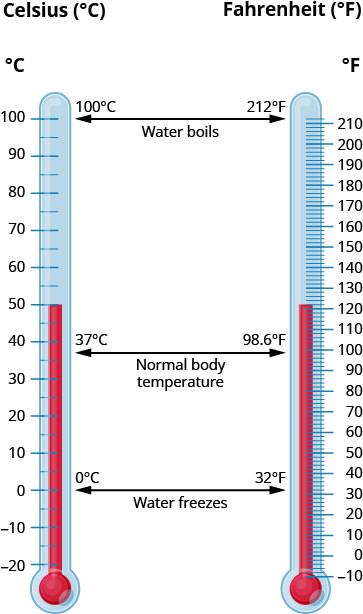
Pour convertir la température Fahrenheit, F, en température Celsius, C, utilisez la formule
\[C = \frac { 5 } { 9 } ( F - 32 )\]
Pour convertir la température Celsius, C, en température Fahrenheit, F, utilisez la formule
\[F = \frac { 9 } { 5 } C + 32\]
Convertissez 50 degrés Fahrenheit en degrés Celsius.
- Réponse
-
Nous allons remplacer 50 °F dans la formule pour trouver C.
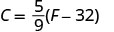

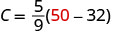
Simplifiez entre parenthèses. 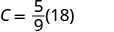
Multipliez. 
Nous avons donc découvert que 50 °F équivaut à 10 °C.
Convertir la température Fahrenheit en degrés Celsius : 59° Fahrenheit.
- Réponse
-
15 °C
Convertir la température Fahrenheit en degrés Celsius : 41° Fahrenheit.
- Réponse
-
5 °C
Lors de sa visite à Paris, Woody a constaté que la température était de 20 degrés Celsius. Convertissez la température en degrés Fahrenheit.
- Réponse
-
Nous allons remplacer 20 °C dans la formule pour trouver F.
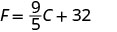

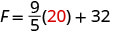
Multipliez. 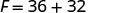
Ajoutez. 
Nous avons donc constaté que 20 °C équivalaient à 68 °F.
Convertissez la température Celsius en degrés Fahrenheit : la température à Helsinki, en Finlande, était de 15 degrés Celsius.
- Réponse
-
59 °F
Convertissez la température Celsius en degrés Fahrenheit : la température à Sydney, en Australie, était de 10 degrés Celsius.
- Réponse
-
50 °F
Concepts clés
- Système de mesure métrique
- Longueur
1 kilomètre (km) = 1 000 m
1 hectomètre (hm) = 100 m
1 de diamètre (barrage) = 10 m
1 mètre (m) = 1 m
1 décimètre (dm) = 0,1 m
1 centimètre (cm) = 0,01 m
1 millimètre (mm) = 0,001 m
1 mètre = 100 centimètres
1 mètre = 1 000 millimètres
- Masse
1 kilogramme (kg) =
1 000 g 1 hectogramme (hg) = 100 g
1 décigramme (jour) = 10 g
1 gramme (g) = 1 g
1 décigramme (dg) = 0,1 g
1 centigramme (cg) = 0,01 g
1 milligramme (mg) = 0,001 g
1 gramme = 100 centigrammes
1 gramme = 1 000 milligrammes
- Capacité
1 kilolitre (kL) = 1 000 L
1 hectolitre (hL) = 100 L
1 dékalitre (dAL) = 10 L
1 litre (L) = 1 L
1 décilitre (dL) = 0,1 L
1 centilitre (cL) = 0,01 L
1 millilitre (mL) = 0,001 L
1 litre = 100 centilitres
1 litre = 1 000 millilitres
- Conversion de température
- Pour convertir la température Fahrenheit, F, en température Celsius, C, utilisez la formule\(C=\frac{5}{9}(F−32)\)
- Pour convertir la température Celsius, C, en température Fahrenheit, F, utilisez la formule\(F=\frac{9}{5}C+32\)


