1.5 : Multiplier et diviser des entiers
- Page ID
- 195221
À la fin de cette section, vous serez en mesure de :
- Multipliez des entiers
- Diviser des nombres entiers
- Simplifier les expressions avec des entiers
- Evaluer des expressions variables avec des nombres entiers
- Traduisez des phrases anglaises en expressions algébriques
- Utiliser des nombres entiers dans les applications
Vous trouverez une introduction plus complète aux sujets abordés dans cette section dans le chapitre Préalgèbre, Entiers.
Multipliez des entiers
Comme la multiplication est un raccourci mathématique désignant les additions répétées, notre modèle peut facilement être appliqué pour montrer la multiplication d'entiers. Examinons ce modèle concret pour voir quels modèles nous remarquons. Nous utiliserons les mêmes exemples que ceux que nous avons utilisés pour l'addition et la soustraction. Ici, nous utiliserons le modèle uniquement pour nous aider à découvrir le modèle.
Nous nous souvenons que\(a\cdot b\) cela signifie ajouter des\(a,\, b\) temps. Ici, nous utilisons le modèle uniquement pour nous aider à découvrir le modèle.
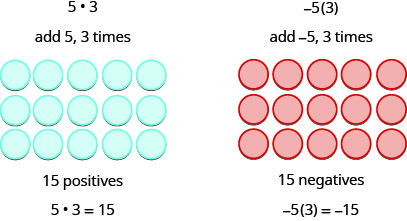
Les deux exemples suivants sont plus intéressants.
Qu'est-ce que cela signifie de multiplier\(5\) par\(−3\) ? Cela signifie soustraire les\(5, 3\) temps. Considérer la soustraction comme « à emporter » signifie enlever du\(5, 3\) temps. Mais il n'y a rien à retirer, nous commençons donc par ajouter des paires neutres sur l'espace de travail. Ensuite, nous l'\(5\)emportons trois fois.
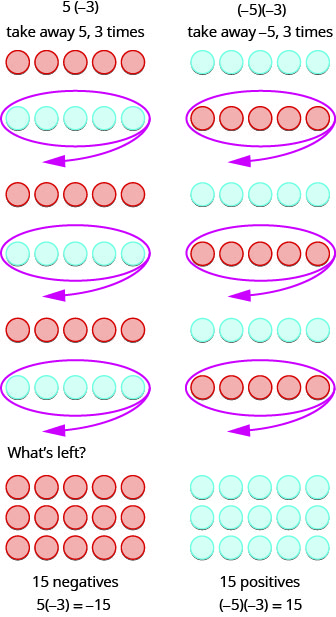
En résumé :
\[\begin{array} {ll} {5 \cdot 3 = 15} &{-5(3) = -15} \\ {5(-3) = -15} &{(-5)(-3) = 15} \end{array}\]
Notez que pour la multiplication de deux nombres signés, lorsque :
- les signes sont les mêmes, le produit est positif.
- les signes sont différents, le produit est négatif.
Nous allons rassembler tout cela dans le tableau ci-dessous.
Pour la multiplication de deux nombres signés :
| Mêmes signes | Produit | Exemple |
|---|---|---|
| Deux points positifs | positif | \(7\cdot 4 = 28\) |
| Deux points négatifs | positif | \(-8(-6) = 48\) |
| Différents signes | Produit | Exemple |
|---|---|---|
| Points positifs et\(\cdot\) négatifs | NÉGATIF | \(7(-9) = -63\) |
| \(\cdot\)Points positifs négatifs | NÉGATIF | \(-5\cdot 10= -50\) |
Multipliez :
- \(-9\cdot 3\)
- \(-2(-5)\)
- \(4(-8)\)
- \(7\cdot 6\)
- Réponse
-
- \[\begin{array} {ll} {} &{-9\cdot 3} \\ {\text{Multiply, noting that the signs are different, so the product is negative.}} &{-27} \end{array}\]
- \[\begin{array} {ll} {} &{-2(-5)} \\ {\text{Multiply, noting that the signs are same, so the product is positive.}} &{10} \end{array}\]
- \[\begin{array} {ll} {} &{4(-8)} \\ {\text{Multiply, with different signs.}} &{-32} \end{array}\]
- \[\begin{array} {ll} {} &{7\cdot 6} \\ {\text{Multiply, with different signs.}} &{42} \end{array}\]
Multipliez :
- \(-6\cdot 8\)
- \(-4(-7)\)
- \(9(-7)\)
- \(5\cdot 12\)
- Réponse
-
- \(-48\)
- \(28\)
- \(-63\)
- \(60\)
Multipliez :
- \(-8\cdot 7\)
- \(-6(-9)\)
- \(7(-4)\)
- \(3\cdot 13\)
- Réponse
-
- \(-56\)
- \(54\)
- \(-28\)
- \(39\)
Lorsque nous multiplions un nombre par\(1\), le résultat est le même nombre. Que se passe-t-il lorsque nous multiplions un nombre par\(−1\) ? Multiplions un nombre positif puis un nombre négatif par\(−1\) pour voir ce que nous obtenons.
\[\begin{array} {lll} {} &{-1\cdot 4} &{-1(-3)}\\ {\text{Multiply.}} &{-4} &{3} \\ {} &{-4\text{ is the opposite of 4.}} &{3\text{ is the opposite of } -3} \end{array}\]
Chaque fois qu'on multiplie un nombre par\(−1\), on obtient son contraire !
MULTIPLICATION PAR −1
\[−1a=−a\]
Multiplier un nombre par\(−1\) donne son contraire.
Multipliez :
- \(-1 \cdot 7\)
- \(-1(-11)\)
- Réponse
-
- \[\begin{array} {ll} {} &{-1\cdot 7} \\ {\text{Multiply, noting that the signs are different}} &{-7} \\ {\text{so the product is negative.}} &{-7\text{ is the opposite of 7.}} \end{array}\]
- \[\begin{array} {ll} {} &{-1(-11)} \\ {\text{Multiply, noting that the signs are different}} &{11} \\ {\text{so the product is positive.}} &{11\text{ is the opposite of -11.}} \end{array}\]
Multipliez :
- \(-1\cdot 9\)
- \(-1\cdot(-17)\)
- Réponse
-
- \(-9\)
- \(17\)
Multipliez :
- \(-1\cdot 8\)
- \(-1\cdot(-16)\)
- Réponse
-
- \(-8\)
- \(16\)
Diviser des nombres entiers
Qu'en est-il de la division ? La division est l'opération inverse de la multiplication. Donc,\(15\div 3=5\) parce que\(5 \cdot 3 = 15\). En mots, cette expression indique que l'\(15\)on peut le diviser en trois groupes de cinq chacun parce que l'ajout de cinq trois fois donne\(15\). Regardez quelques exemples de multiplication d'entiers pour déterminer les règles de division des entiers.
\[\begin{array} {ll} {5\cdot 3 = 15\text{ so }15\div 3 = 5} &{-5(3) = -15\text{ so }-15\div 3 = -5} \\ {(-5)(-3) = 15\text{ so }15\div (-3) = -5} &{5(-3) = -15\text{ so }-15\div (-3) = 5} \end{array}\]
La division suit les mêmes règles que la multiplication !
Pour la division de deux numéros signés, lorsque :
- les signes sont les mêmes, le quotient est positif.
- les signes sont différents, le quotient est négatif.
Et n'oubliez pas que nous pouvons toujours vérifier la réponse à un problème de division en multipliant.
Pour la multiplication et la division de deux nombres signés :
- Si les signes sont identiques, le résultat est positif.
- Si les signes sont différents, le résultat est négatif.
| Mêmes signes | Résultat |
|---|---|
| Deux points positifs | positif |
| Deux points négatifs | positif |
| Si les signes sont identiques, le résultat est positif. | |
| Différents signes | Résultat |
|---|---|
| Positif et négatif | NÉGATIF |
| Négatif et positif | NÉGATIF |
| Si les signes sont différents, le résultat est négatif. | |
- \(-27\div 3\)
- \(-100\div (-4)\)
- Réponse
-
- \[\begin{array} {ll} {} &{-27 \div 3} \\ {\text{Divide, with different signs, the quotient is}} &{-9} \\ {\text{negative.}} &{} \end{array}\]
- \[\begin{array} {ll} {} &{-100 \div (-4)} \\ {\text{Divide, with signs that are the same the}} &{25} \\ {\text{ quotient is negative.}} &{} \end{array}\]
Diviser :
- \(-42\div 6\)
- \(-117\div (-3)\)
- Réponse
-
- \(-7\)
- \(39\)
Diviser :
- \(-63\div 7\)
- \(-115\div (-5)\)
- Réponse
-
- \(-9\)
- \(23\)
Simplifier les expressions avec des entiers
Que se passe-t-il lorsqu'il y a plus de deux nombres dans une expression ? L'ordre des opérations s'applique toujours lorsque des négatifs sont inclus. Tu te souviens de ma chère tante Sally ?
Essayons quelques exemples. Nous allons simplifier les expressions qui utilisent les quatre opérations avec des nombres entiers : addition, soustraction, multiplication et division. N'oubliez pas de suivre l'ordre des opérations.
Simplifiez :
\(7(-2)+4(-7)-6\)
- Réponse
-
\[\begin{array} {ll} {} &{7(-2)+4(-7)-6} \\ {\text{Multiply first.}} &{-14+(-28)-6} \\ {\text{Add.}} &{-42-6} \\{\text{Subtract}} &{-48} \end{array}\]
Simplifiez :
\(8(-3)+5(-7)-4\)
- Réponse
-
\(-63\)
Simplifiez :
\(9(-3)+7(-8)-1\)
- Réponse
-
\(-84\)
Simplifiez :
- \((-2)^{4}\)
- \(-2^{4}\)
- Réponse
-
- \[\begin{array} {ll} {} &{(-2)^{4}} \\ {\text{Write in expanded form.}} &{(-2)(-2)(-2)(-2)} \\ {\text{Multiply}} &{4(-2)(-2)} \\{\text{Multiply}} &{-8(-2)} \\{\text{Multiply}} &{16} \end{array}\]
- \[\begin{array} {ll} {} &{-2^{4}} \\ {\text{Write in expanded form. We are asked to find the opposite of }2^{4}.} &{-(2\cdot 2\cdot 2 \cdot 2)} \\ {\text{Multiply}} &{-(4\cdot 2\cdot 2)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Multiply}} &{-16} \end{array}\]
Remarquez la différence entre les parties (1) et (2). Dans la partie (1), l'exposant signifie élever ce qui est entre parenthèses\((−2)\) à la\(4^{th}\) puissance. Dans la partie (2), l'exposant signifie monter juste\(2\) à la\(4^{th}\) puissance, puis prendre l'inverse.
Simplifiez :
- \((-3)^{4}\)
- \(-3^{4}\)
- Réponse
-
- \(81\)
- \(-81\)
Simplifiez :
- \((-7)^{2}\)
- \(-7^{2}\)
- Réponse
-
- \(49\)
- \(-49\)
L'exemple suivant nous rappelle de commencer par simplifier les parenthèses entre parenthèses.
Simplifiez :
\(12-3(9 - 12)\)
- Réponse
-
\[\begin{array} {llll} {} &{12-3(9 - 12)} \\ {\text{Subtract parentheses first}} &{12-3(-3)} \\ {\text{Multiply.}} &{12-(-9)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Subtract}} &{21} \end{array}\]
Simplifiez :
\(17 - 4(8 - 11)\)
- Réponse
-
\(29\)
Simplifiez :
\(16 - 6(7 - 13)\)
- Réponse
-
\(52\)
Simplifiez :
\(8(-9)\div (-2)^{3}\)
- Réponse
-
\[\begin{array} {ll} {} &{8(-9)\div(-2)^{3}} \\ {\text{Exponents first}} &{8(-9)\div(-8)} \\ {\text{Multiply.}} &{-72\div (-8)} \\{\text{Divide}} &{9} \end{array}\]
Simplifiez :
\(12(-9)\div (-3)^{3}\)
- Réponse
-
\(4\)
Simplifiez :
\(18(-4)\div (-2)^{3}\)
- Réponse
-
\(9\)
Simplifiez :
\(-30\div 2 + (-3)(-7)\)
- Réponse
-
\[\begin{array} {ll} {} &{-30\div 2 + (-3)(-7)} \\ {\text{Multiply and divide left to right, so divide first.}} &{-15+(-3)(-7)} \\ {\text{Multiply.}} &{-15+ 21} \\{\text{Add}} &{6} \end{array}\]
Simplifiez :
\(-27\div 3 + (-5)(-6)\)
- Réponse
-
\(21\)
Simplifiez :
\(-32\div 4 + (-2)(-7)\)
- Réponse
-
\(6\)
Evaluer des expressions variables avec des nombres entiers
N'oubliez pas que pour évaluer une expression, vous devez substituer un nombre à la variable de l'expression. Nous pouvons maintenant utiliser des nombres négatifs aussi bien que des nombres positifs.
Quand\(n=−5\), évaluez :
- \(n+1\)
- \(−n+1\).
- Réponse
-
- \[\begin{array} {ll} {} &{n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-5+1} \\ {\text{Simplify.}} &{-4} \end{array}\]
- \[\begin{array} {ll} {} &{-n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-(-5)+1} \\ {\text{Simplify.}} &{-4} \\{\text{Add.}} &{6} \end{array}\]
Quand\(n=−8\), évaluez :
- \(n+2\)
- \(−n+2\).
- Réponse
-
- \(-6\)
- \(10\)
Quand\(y=−9\), évaluez :
- \(y+8\)
- \(−y+8\).
- Réponse
-
- \(-1\)
- \(17\)
Évaluez\((x+y)^{2}\) quand\(x = -18\) et\(y = 24\).
- Réponse
-
\[\begin{array} {ll} {} &{(x+y)^{2}} \\ {\text{Substitute }-18\text{ for }x \text{ and } 24 \text{ for } y} &{(-18 + 24)^{2}} \\ {\text{Add inside parentheses}} &{(6)^{2}} \\{\text{Simplify.}} &{36} \end{array}\]
Évaluez\((x+y)^{2}\) quand\(x = -15\) et\(y = 29\).
- Réponse
-
\(196\)
Évaluez\((x+y)^{3}\) quand\(x = -8\) et\(y = 10\).
- Réponse
-
\(8\)
Évaluez\(20 -z \) quand
- \(z = 12\)
- \(z = -12\)
- Réponse
-
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }12\text{ for }z.} &{20 - 12} \\ {\text{Subtract}} &{8} \end{array}\]
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }-12\text{ for }z.} &{20 - (-12)} \\ {\text{Subtract}} &{32} \end{array}\]
Évaluez\(17 - k\) quand
- \(k = 19\)
- \(k = -19\)
- Réponse
-
- \(-2\)
- \(36\)
Évaluez\(-5 - b\) quand
- \(b = 14\)
- \(b = -14\)
- Réponse
-
- \(-19\)
- \(9\)
Évaluez :
\(2x^{2} + 3x + 8\)quand\(x = 4\).
- Réponse
-
Substitut\(4\) de\(x\). Utilisez des parenthèses pour montrer la multiplication.
\[\begin{array} {ll} {} &{2x^{2} + 3x + 8} \\ {\text{Substitute }} &{2(4)^{2} + 3(4) + 8} \\ {\text{Evaluate exponents.}} &{2(16) + 3(4) + 8} \\ {\text{Multiply.}} &{32 + 12 + 8} \\{\text{Add.}} &{52} \end{array}\]
Évaluez :
\(3x^{2} - 2x + 6\)quand\(x =-3\).
- Réponse
-
\(39\)
Évaluez :
\(4x^{2} - x - 5\)quand\(x = -2\).
- Réponse
-
\(13\)
Traduisez des phrases en expressions avec des nombres entiers
Nos travaux antérieurs sur la traduction de l'anglais en algèbre s'appliquent également aux phrases qui incluent à la fois des nombres positifs et négatifs.
Traduisez et simplifiez : la somme de\(8\) et\(−12\), augmentée de\(3\).
- Réponse
-
\[\begin{array} {ll} {} &{\text{the } \textbf{sum} \text{of 8 and -12, increased by 3}} \\ {\text{Translate.}} &{[8 + (-12)] + 3} \\ {\text{Simplify. Be careful not to confuse the}} &{(-4) + 3} \\{\text{brackets with an absolute value sign.}} \\{\text{Add.}} &{-1} \end{array}\]
Traduisez et simplifiez : la somme de\(9\) et\(−16\), augmentée de\(4\).
- Réponse
-
\((9 + (-16)) + 4 - 3\)
Traduisez et simplifiez : la somme de\(-8\) et\(−12\), augmentée de\(7\).
- Réponse
-
\((-8 + (-12)) + 7 - 13\)
Lorsque nous avons introduit les symboles d'opération pour la première fois, nous avons constaté que l'expression pouvait être lue de plusieurs manières. Ils sont listés dans le tableau ci-dessous.
| \(a−b\) |
|---|
| \ (a−b \) » data-valign="top">\(a\) moins\(b\) la différence de\(a\) et\(b\) \(b\) soustraite de\(a\) \(b\) moins de\(a\) |
Veillez à placer a et b dans le bon ordre !
Traduisez puis simplifiez
- la différence entre\(13\) et\(−21\)
- soustraire\(24\) de\(−19\).
- Réponse
-
- \[\begin{array} {ll} {} &{\text{the } \textbf{difference } \text{of 13 and -21}} \\ {\text{Translate.}} &{13 - (-21)} \\ {\text{Simplify.}} &{34} \end{array}\]
- \[\begin{array} {ll} {} &\textbf{subtract }24 \textbf{ from }-19 \\ {\text{Translate.}} &{-19 - 24} \\ {\text{Remember, subtract b from a means }a - b} &{} \\{\text{Simplify.}} &{-43} \end{array}\]
Traduire et simplifier
- la différence entre\(14\) et\(−23\)
- soustraire\(21\) de\(−17\).
- Réponse
-
- \(14 - (-23); 37\)
- \(-17 - 21; -38\)
Traduire et simplifier
- la différence entre\(11\) et\(−19\)
- soustraire\(18\) de\(−11\).
- Réponse
-
- \(11 - (-19); 30\)
- \(-11 - 18; -29\)
Encore une fois, nos travaux antérieurs de traduction de l'anglais en algèbre se transfèrent à des phrases qui incluent à la fois des nombres entiers multiplicateurs et diviseurs. N'oubliez pas que le mot clé pour la multiplication est « produit » et pour la division, « quotient ».
Traduisez en une expression algébrique et simplifiez si possible : le produit de\(−2\) et\(14\).
- Réponse
-
\[\begin{array} {ll} {} &{\text{the product of }-2 \text{ and } 14} \\ {\text{Translate.}} &{(-2)(14)} \\{\text{Simplify.}} &{-28} \end{array}\]
Traduisez en une expression algébrique et simplifiez si possible : le produit de\(−5\) et\(12\).
- Réponse
-
\(-5(12); -60\)
Traduisez en une expression algébrique et simplifiez si possible : le produit de\(8\) et\(-13\).
- Réponse
-
\(-8(13); -104\)
Traduisez en une expression algébrique et simplifiez si possible : le quotient de\(−56\) et\(−7\).
- Réponse
-
\[\begin{array} {ll} {} &{\text{the quotient of }-56 \text{ and } -7} \\ {\text{Translate.}} &{-56\div(-7)} \\{\text{Simplify.}} &{8} \end{array}\]
Traduisez en une expression algébrique et simplifiez si possible : le quotient de\(−63\) et\(−9\).
- Réponse
-
\(-63\div (-9); 7\)
Traduisez en une expression algébrique et simplifiez si possible : le quotient de\(−72\) et\(−9\).
- Réponse
-
\(-72\div (-9); 8\)
Utiliser des nombres entiers dans les applications
Nous allons présenter un plan pour résoudre les demandes. Il est difficile de trouver quelque chose si l'on ne sait pas ce que l'on cherche ou comment l'appeler ! Ainsi, lorsque nous résolvons une application, nous devons d'abord déterminer ce que le problème nous demande de trouver. Ensuite, nous allons écrire une phrase qui donne les informations nécessaires pour le trouver. Nous allons traduire la phrase en expression, puis simplifier l'expression pour obtenir la réponse. Enfin, nous résumons la réponse en une phrase pour nous assurer qu'elle a du sens.
Comment appliquer une stratégie pour résoudre des applications avec des nombres entiers
La température à Urbana, dans l'Illinois, un matin était de\(11\) degrés. En milieu d'après-midi, la température avait chuté à quelques\(−9\) degrés. Quelle était la différence entre les températures du matin et de l'après-midi ?
- Réponse
-
Étape 1 Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris. Étape 2 Identifiez ce que l'on nous demande de trouver. la différence entre les températures du matin et de l'après-midi Étape 3 Écrivez une phrase qui donne les informations nécessaires pour le trouver. la différence entre\(11\) et\(-9\) Étape 4. Traduisez la phrase en expression. \(11 - (-9)\) Étape 5. Simplifiez l'expression. \(20\) Étape 6. Écrivez une phrase complète qui répond à la question. La différence de température était de 20 degrés.
La température à Anchorage, en Alaska, un matin était de\(15\) degrés. En milieu d'après-midi, la température était tombée à des\(30\) degrés en dessous de zéro. Quelle était la différence entre les températures du matin et de l'après-midi ?
- Réponse
-
La différence de température était de\(45\) degrés.
La température à Denver était de\(−6\) degrés à l'heure du déjeuner. Au coucher du soleil, la température avait chuté à\(−15\) quelques degrés. Quelle était la différence entre les températures au déjeuner et au coucher du soleil ?
- Réponse
-
La différence de température était de\(9\) degrés.
- Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris
- Identifiez ce que l'on nous demande de trouver.
- Écrivez une phrase qui donne les informations nécessaires pour le trouver.
- Traduisez la phrase en expression.
- Simplifiez l'expression.
- Répondez à la question par une phrase complète.
L'équipe de football des Mustangs a écopé de trois pénalités au troisième quart. Chaque pénalité leur a valu une perte de quinze mètres. Quel est le nombre de mètres perdus ?
- Réponse
-
Étape 1 Lisez le problème. Assurez-vous que tous les mots et toutes les idées sont compris. Étape 2 Identifiez ce que l'on nous demande de trouver. le nombre de mètres perdus Étape 3 Écrivez une phrase qui donne les informations nécessaires pour le trouver. trois fois une pénalité\(15\) de 3 yards Étape 4. Traduisez la phrase en expression. \(3(-15)\) Étape 5. Simplifiez l'expression. \(-45\) Étape 6. Écrivez une phrase complète qui répond à la question. L'équipe a perdu des\(45\) mètres.
Les Bears ont mal joué et ont écopé de sept pénalités dans le match. Chaque pénalité a entraîné une perte de\(15\) mètres. Quel est le nombre de mètres perdus à cause des pénalités ?
- Réponse
-
Les Bears ont perdu des\(105\) mètres.
Bill utilise le guichet automatique sur le campus parce que c'est pratique. Cependant, chaque fois qu'il l'utilise, il doit payer des frais de 2$. Le mois dernier, il a utilisé le guichet automatique huit fois. Quel était le montant total de ses frais d'utilisation du guichet automatique ?
- Réponse
-
Des frais de 16$ ont été déduits de son compte courant.
Concepts clés
- Multiplication et division de deux nombres signés
- Mêmes signes : le produit est positif
- Signes différents : le produit est négatif
- Stratégie pour les applications
- Identifiez ce que l'on vous demande de trouver.
- Écrivez une phrase qui donne les informations nécessaires pour le trouver.
- Traduisez la phrase en expression.
- Simplifiez l'expression.
- Répondez à la question par une phrase complète.


