16.7 : Théorème de Stokes
- Page ID
- 197856
- Expliquez la signification du théorème de Stokes.
- Utilisez le théorème de Stokes pour évaluer une intégrale linéaire.
- Utilisez le théorème de Stokes pour calculer une intégrale de surface.
- Utilisez le théorème de Stokes pour calculer une boucle.
Dans cette section, nous étudions le théorème de Stokes, une généralisation dimensionnelle supérieure du théorème de Green. Ce théorème, comme le théorème fondamental des intégrales linéaires et le théorème de Green, est une généralisation du théorème fondamental du calcul à des dimensions supérieures. Le théorème de Stokes relie une intégrale de surface vectorielle au-dessus de la surface de l'espace\(S\) à une droite intégrale autour de la limite de\(S\). Par conséquent, tout comme les théorèmes précédents, le théorème de Stokes peut être utilisé pour réduire une intégrale sur un objet géométrique\(S\) à une intégrale au-dessus de la limite de\(S\). En plus de nous permettre de traduire entre les intégrales linéaires et les intégrales de surface, le théorème de Stokes relie les concepts de courbure et de circulation. De plus, le théorème a des applications en mécanique des fluides et en électromagnétisme. Nous utilisons le théorème de Stokes pour dériver la loi de Faraday, un résultat important impliquant des champs électriques.
Théorème de Stokes
Le théorème de Stokes indique que nous pouvons calculer le flux de\( curl \,\vecs{F}\) surface\(S\) en ne connaissant que des informations sur les valeurs du\(\vecs{F}\) long de la limite de\(S\). Inversement, nous pouvons calculer l'intégrale linéaire du champ vectoriel\(\vecs{F}\) le long de la limite de la surface\(S\) en effectuant une translation vers une double intégrale de la courbure de\(\vecs{F}\) dessus\(S\).
\(S\)Soit une surface lisse orientée avec un vecteur normal unitaire\(\vecs{N}\). De plus, supposons que la limite de\(S\) est une simple courbe fermée\(C\). L'orientation de\(S\) induit l'orientation positive\(C\) si, lorsque vous marchez dans la direction positive, la tête\(C\) pointée dans la direction de\(\vecs{N}\), la surface est toujours sur votre gauche. Une fois cette définition en place, nous pouvons énoncer le théorème de Stokes.
\(S\)Soit une surface orientée lisse par morceaux avec une limite qui est une simple courbe fermée\(C\) avec une orientation positive (Figure\(\PageIndex{1}\)). S'il s'\(\vecs{F}\)agit d'un champ vectoriel avec des fonctions constitutives qui ont des dérivées partielles continues sur une région ouverte contenant\(S\), alors
\[\int_C \vecs{F} \cdot d \vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs S. \label{Stokes1} \]
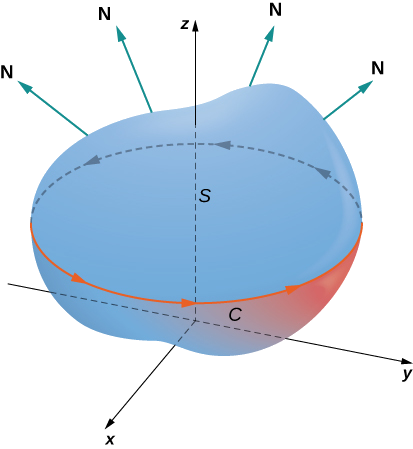
Supposons que la surface\(S\) soit une région plane du\(xy\) plan orientée vers le haut. Alors le vecteur normal unitaire est une intégrale\(\vecs{k}\) de surface
\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]
est en fait la double intégrale
\[\iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber \]
Dans ce cas particulier, le théorème de Stokes donne
\[\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber \]
Cependant, il s'agit de la forme de flux du théorème de Green, qui nous montre que le théorème de Green est un cas particulier du théorème de Stokes. Le théorème de Green ne peut traiter que des surfaces dans un plan, tandis que le théorème de Stokes peut traiter des surfaces dans un plan ou dans l'espace.
La preuve complète du théorème de Stokes dépasse le cadre de ce texte. Nous examinons une explication intuitive de la véracité du théorème, puis nous voyons la preuve du théorème dans le cas particulier où la surface\(S\) est une partie du graphe d'une fonction, et\(S\) que la limite de\(S\), et\(\vecs{F}\) sont toutes assez apprivoisées.
Tout d'abord, nous examinons une preuve informelle du théorème. Cette preuve n'est pas rigoureuse, mais elle vise à donner une idée générale de la raison pour laquelle le théorème est vrai. Soit\(S\) une surface et\(D\) soit un petit morceau de surface afin qu'il\(D\) ne partage aucun point avec la limite de\(S\). Nous avons choisi\(D\) d'être suffisamment petit pour pouvoir être approximé par un carré orienté\(E\). Laissons\(D\) hériter de\(S\) son orientation et donner\(E\) la même orientation. Ce carré a quatre côtés ; indiquez-les\(E_l, \, E_r, \, E_u\), et\(E_d\) pour les côtés gauche, droit, haut et bas, respectivement. Sur le carré, nous pouvons utiliser la forme de flux du théorème de Green :
\[\int_{E_l+E_d+E_r+E_u} \vecs{F} \cdot d \vecs{r} = \iint_E curl \, \vecs{F} \cdot \vecs{N} \, d \vecs{S} = \iint_E curl \, \vecs{F} \cdot d\vecs{S}. \nonumber \]
Pour approximer le flux sur toute la surface, nous ajoutons les valeurs du flux sur les petits carrés approximatifs de petites parties de la surface (Figure\(\PageIndex{2}\)).
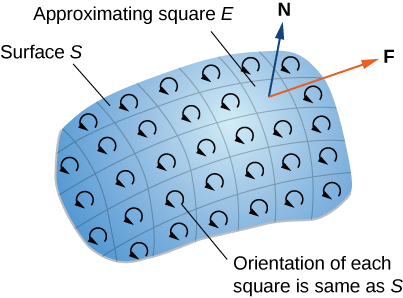
Selon le théorème de Green, le flux à travers chaque carré approximatif est une droite intégrale au-dessus de sa limite. \(F\)Soit un carré approximatif avec une orientation héritée de\(S\) et avec un côté droit\(E_l\) (\(F\)donc à gauche de\(E\)). \(F_r\)Soit le côté droit de\(F\) ; puis,\(E_l = - F_r\). En d'autres termes, le côté droit de\(F\) est la même courbe que le côté gauche de\(E\), juste orienté dans la direction opposée. Par conséquent,
\[\int_{E_l} \vecs F \cdot d\vecs r = - \int_{F_r} \vecs F \cdot d\vecs r. \nonumber \]
Lorsque nous additionnons tous les flux sur tous les carrés, en approximant les intégrales de surface\(S\), de ligne
\[\int_{E_l} \vecs{F} \cdot d \vecs{r} \nonumber \]
et
\[ \int_{F_r} \vecs{F} \cdot d\vecs{r} \nonumber \]
annulez-vous mutuellement. Il en va de même pour les intégrales de ligne sur les trois autres côtés de\(E\). Ces trois intégrales linéaires s'annulent avec l'intégrale de droite du côté inférieur du carré au-dessus\(E\), l'intégrale de droite au-dessus du côté gauche du carré à droite du\(E\) carré et l'intégrale de droite au-dessus du côté supérieur du carré inférieur\(E\) (Figure\(\PageIndex{3}\)). Une fois que toute cette annulation se produit sur tous les carrés approximatifs, les seules intégrales de ligne qui subsistent sont les intégrales de ligne sur les côtés approchant la limite de\(S\). Par conséquent, la somme de tous les flux (qui, selon le théorème de Green, est la somme de toutes les intégrales linéaires autour des limites des carrés approximatifs) peut être approximée par une intégrale droite au-dessus de la limite de\(S\). Dans la limite, lorsque les aires des carrés approximatifs atteignent zéro, cette approximation se rapproche arbitrairement du flux.
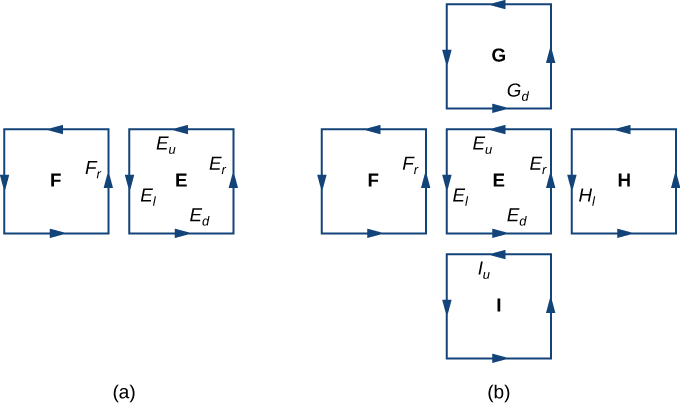
Examinons maintenant une preuve rigoureuse du théorème dans le cas particulier qu'\(S\)est le graphe de la fonction\(z = f(x,y)\), où\(x\) et\(y\) varient sur une région bornée et simplement connectée\(D\) d'une aire finie (Figure\(\PageIndex{4}\)). Supposons en outre qu'il\(f\) possède des dérivées partielles continues du second ordre. \(C\)Dénotons la limite de\(S\) et\(C'\) notons la limite de\(D\). Ensuite,\(D\) est « l'ombre » de\(S\) dans l'avion et\(C'\) est « l'ombre » de\(C\). Supposons que cela\(S\) soit orienté vers le haut. L'orientation dans le sens antihoraire de\(C\) est positive, tout comme l'orientation antihoraire de\(C'\). \(\vecs F(x,y,z) = \langle P,Q,R \rangle\)Soit un champ vectoriel dont les fonctions constitutives ont des dérivées partielles continues.
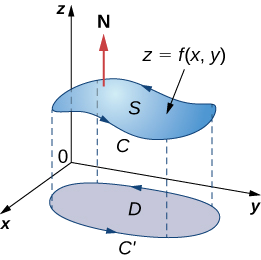
Nous prenons le paramétrage standard de\(S \, : \, x = x, \, y = y, \, z = g(x,y)\). Les vecteurs tangents sont\(\vecs t_x = \langle 1,0,g_x \rangle\)\(\vecs t_y = \langle 0,1,g_y \rangle\) et donc\(\vecs t_x \times \vecs t_y = \langle -g_x, \, -g_y, \, 1 \rangle\).
\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} = \iint_D [- (R_y - Q_z)z_x - (P_z - R_x)z_y + (Q_x - P_y)] \, dA, \nonumber \]
où les dérivées partielles sont toutes évaluées à\((x,y,g(x,y))\), ce qui rend l'integrand dépendant de\(x\) et\(y\) uniquement. Supposons\(\langle x (t), \, y(t) \rangle, \, a \leq t \leq b\) qu'il s'agisse d'un paramétrage de\(C'\). Ensuite, un paramétrage de\(C\) is\(\langle x (t), \, y(t), \, g(x(t), \, y(t))\rangle, \, a \leq t \leq b\). Armés de ces paramétrisations, de la règle de la chaîne et du théorème de Green, et en gardant à l'esprit que\(P\),\(Q\) et\(R\) sont toutes des fonctions de\(x\) et\(y\), nous pouvons évaluer l'intégrale de la ligne
\[ \begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_a^b (Px'(t) + Qy'(t) + Rz'(t)) \, dt \\[4pt] &= \int_a^b \left[Px'(t) + Qy'(t) + R\left(\dfrac{\partial z}{\partial x} \dfrac{dx}{dt} + \dfrac{\partial z}{\partial y} \dfrac{dy}{dt}\right) \right] dt \\[4pt] &= \int_a^b \left[ \left(P + R \dfrac{\partial z}{\partial x} \right) x' (t) + \left(Q + R \dfrac{\partial z}{\partial y} \right) y'(t) \right] dt \\[4pt] &= \int_{C'} \left(P + R \dfrac{\partial z}{\partial x} \right)\, dx + \left(Q + R \dfrac{\partial z}{\partial y} \right) \, dy \\[4pt] &= \iint_D \left[ \dfrac{\partial}{\partial x} \left( Q + R \dfrac{\partial z}{\partial y} \right) - \dfrac{\partial}{\partial y} \left(P + R \dfrac{\partial z}{\partial x} \right) \right] \, dA \\[4pt] &=\iint_D \left(\dfrac{\partial Q}{\partial x} + \dfrac{\partial Q}{\partial z} \dfrac{\partial z}{\partial x} + \dfrac{\partial R}{\partial x} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z}\dfrac{\partial z}{\partial x} \dfrac{\partial z}{\partial y} + R \dfrac{\partial^2 z}{\partial x \partial y} \right) - \left(\dfrac{\partial P}{\partial y} + \dfrac{\partial P}{\partial z} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z} \dfrac{\partial z}{\partial y} \dfrac{\partial z}{\partial x} + R \dfrac{\partial^2 z}{\partial y \partial x} \right) \end{align*} \nonumber \]
Selon le théorème de Clairaut,
\[\dfrac{\partial^2 z}{\partial x \partial y} = \dfrac{\partial^2 z}{\partial y \partial x} \nonumber \]
Par conséquent, quatre des termes disparaissent de cette double intégrale, et il nous reste
\[\iint_D [- (R_y - Q_z)Z_x - (P_z - R_x) z_y + (Q_x - P_y)] \, dA, \nonumber \]
ce qui équivaut à
\[\iint_S curl \, \vecs{F} \cdot d\vecs{S}. \nonumber \]
\(\Box\)
Nous avons montré que le théorème de Stokes est vrai dans le cas d'une fonction dont le domaine est une région simplement connectée d'une surface finie. Nous pouvons rapidement confirmer ce théorème pour un autre cas important : lorsque le champ vectoriel\(\vecs{F}\) est un champ conservateur. Si\(\vecs{F}\) c'est conservateur, la courbure de\(\vecs{F}\) est nulle, donc
\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} = 0. \nonumber \]
Puisque la limite de\(S\) est une courbe fermée, l'intégrale
\[\int_C \vecs{F} \cdot d\vecs{r}. \nonumber \]
est également égal à zéro.
Vérifiez que le théorème de Stokes est vrai pour le champ vectoriel\(\vecs{F}(x,y) = \langle -z,x,0 \rangle\) et la surface\(S\), où se\(S\) trouve l'hémisphère, orienté vers l'extérieur, avec un paramétrage\(\vecs r(\phi, \theta) = \langle \sin \phi \, \cos \theta, \, \sin \phi \, \sin \theta, \, \cos \phi \rangle, \, 0 \leq \theta \leq \pi, \, 0 \leq \phi \leq \pi\) comme indiqué sur la figure\(\PageIndex{5}\).
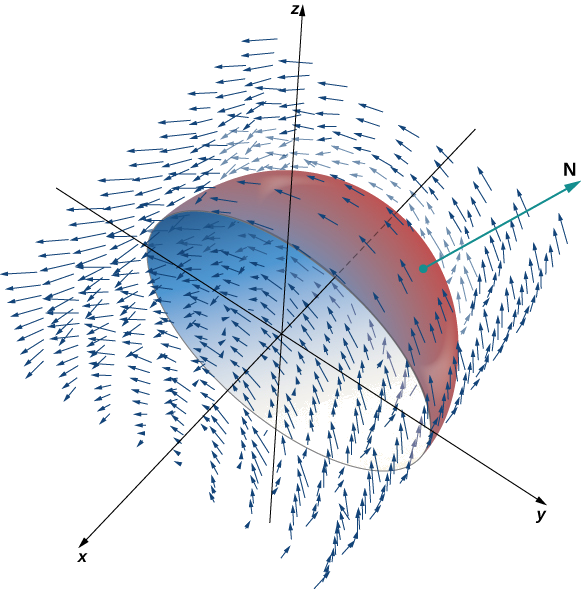
Solution
\(C\)Soyons la limite de\(S\). Notez qu'il\(C\) s'agit d'un cercle de rayon 1, centré à l'origine, situé dans le plan\(y = 0\). Ce cercle est paramétré\(\langle \cos t, \, 0, \, \sin t \rangle, \, 0 \leq t \leq 2\pi\). L'équation des intégrales de surface scalaires
\[ \begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_0^{2\pi} \langle -\sin t, \, \cos t, \, 0 \rangle \cdot \langle - \sin t, \, 0, \, \cos t \rangle \, dt \\[4pt] &= \int_0^{2\pi} \sin^2 t \, dt \\[4pt] &= \pi. \end{align*}\]
Par l'équation des intégrales de lignes vectorielles,
\[ \begin{align*} \iint_S \, curl \, \vecs{F} \cdot d\vecs S &= \iint_D curl \, \vecs{F} (\vecs r (\phi,\theta)) \cdot ( \vecs t_{\phi} \times \vecs t_{\theta}) \, dA \\[4pt] &= \iint_D \langle 0, -1, 1 \rangle \cdot \langle \cos \theta \, \sin^2 \phi, \, \sin \theta \, \sin^2 \phi, \, \sin \phi \, \cos \phi \rangle \, dA \\[4pt] &= \int_0^{\pi} \int_0^{\pi} (\sin \phi \, \cos \phi - \sin \theta \, \sin^2 \phi ) \, d\phi d\theta \\[4pt] &= \dfrac{\pi}{2} \int_0^{\pi} \sin \theta \, d\theta \\[4pt] &= \pi.\end{align*}\]
Nous avons donc vérifié le théorème de Stokes pour cet exemple.
Vérifiez que le théorème de Stokes est vrai pour le champ vectoriel\(\vecs{F}(x,y,z) = \langle y,x,-z \rangle \) et la surface\(S\), où se\(S\) trouve la partie orientée vers le haut du graphe\(f(x,y) = x^2 y\) au-dessus d'un triangle dans le\(xy\) plan avec des sommets\((0,0), \, (2,0)\), et\((0,2)\).
- Allusion
-
Calculez l'intégrale double et l'intégrale linéaire séparément.
- Réponse
-
Les deux intégrales donnent\(-\dfrac{136}{45}\) :
Calculate the line integral
\[\int_C \vecs{F} \cdot d\vecs{r}, \nonumber \]
where \(\vecs{F} = \langle xy, \, x^2 + y^2 + z^2, \, yz \rangle\) and \(C\) is the boundary of the parallelogram with vertices \((0,0,1), \, (0,1,0), \, (2,0,-1)\), and \((2,1,-2)\).
Solution
To calculate the line integral directly, we need to parameterize each side of the parallelogram separately, calculate four separate line integrals, and add the result. This is not overly complicated, but it is time-consuming.
By contrast, let’s calculate the line integral using Stokes’ theorem. Let \(S\) denote the surface of the parallelogram. Note that \(S\) is the portion of the graph of \(z = 1 - x - y\) for \((x,y)\) varying over the rectangular region with vertices \((0,0), \, (0,1), \, (2,0)\), and \((2,1)\) in the \(xy\)-plane. Therefore, a parameterization of \(S\) is \(\langle x,y, \, 1 - x - y \rangle, \, 0 \leq x \leq 2, \, 0 \leq y \leq 1\). The curl of \(\vecs{F}\) is \( \langle -z, \, 0, \, x \rangle\),and Stokes’ theorem and the equation for scalar surface integrals
\[ \begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &= \iint_S curl \, \vecs{F} \cdot d\vecs{S} \\[4pt] &= \int_0^2 \int_0^1 curl \, \vecs{F} (x,y) \cdot (\vecs t_x \times \vecs t_y) \, dy\, dx \\[4pt] &= \int_0^2 \int_0^1 \langle - (1 - x - y), \, 0, \, x \rangle \cdot ( \langle 1, \, 0, -1 \rangle \times \langle 0, \, 1, \, -1 \rangle ) \, dy \,dx \\[4pt] &= \int_0^2 \int_0^1 \langle x + y - 1, \, 0, \, x \rangle \cdot \langle 1, 1, 1 \rangle \, dy \, dx \\[4pt] &= \int_0^2 \int_0^1 2x + y - 1 \, dy \, dx \\[4pt] &= 3.\end{align*} \nonumber \]
Use Stokes’ theorem to calculate line integral
\[\int_C \vecs{F} \cdot d\vecs{r}, \nonumber \]
where \(\vecs{F} = \langle z,x,y \rangle \) and \(C\) is the boundary of a triangle with vertices \((0,0,1), \, (3,0,-2)\), and \((0,1,2)\).
- Hint
-
This triangle lies in plane \(z = 1 - x + y\).
- Answer
-
\(\dfrac{3}{2}\)
Interpretation of Curl
In addition to translating between line integrals and flux integrals, Stokes’ theorem can be used to justify the physical interpretation of curl that we have learned. Here we investigate the relationship between curl and circulation, and we use Stokes’ theorem to state Faraday’s law—an important law in electricity and magnetism that relates the curl of an electric field to the rate of change of a magnetic field.
Recall that if \(C\) is a closed curve and \(\vecs{F}\) is a vector field defined on \(C\), then the circulation of \(\vecs{F}\) around \(C\) is line integral
\[\int_C \vecs{F} \cdot d\vecs{r}. \nonumber \]
If \(\vecs{F}\) represents the velocity field of a fluid in space, then the circulation measures the tendency of the fluid to move in the direction of \(C\).
Let \(\vecs{F}\) be a continuous vector field and let \(D_{\tau}\) be a small disk of radius \(r\) with center \(P_0\) (Figure \(\PageIndex{7}\)). If \(D_{\tau}\) is small enough, then \((curl \, \vecs{F})(P) \approx (curl \, \vecs F)(P_0)\) for all points \(P\) in \(D_{\tau}\) because the curl is continuous. Let \(C_{\tau}\) be the boundary circle of \(D_{\tau}\): By Stokes’ theorem,
\[\int_{C_{\tau}} \vecs{F} \cdot d\vecs{r} = \iint_{D_{\tau}} curl \, \vecs{F} \cdot \vecs{N} \, d\vecs S \approx \iint_{D_{\tau}} (curl \, \vecs{F})(P_0) \cdot \vecs{N} (P_0) \, d\vecs S. \nonumber \]
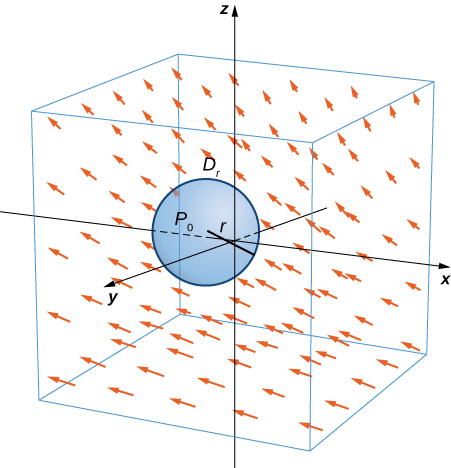
The quantity \( (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \) is constant, and therefore
\[\iint_{D_{\tau}} (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \, d\vecs S = \pi r^2 [(curl \, \vecs F)(P_0) \cdot \vecs N (P_0)]. \nonumber \]
Thus
\[\int_{C_{\tau}} \vecs F \cdot d\vecs r \approx \pi r^2 [ (curl \, \vecs F)(P_0) \cdot \vecs N (P_0)], \nonumber \]
and the approximation gets arbitrarily close as the radius shrinks to zero. Therefore Stokes’ theorem implies that
\[(curl \, \vecs F)(P_0) \cdot \vecs N (P_0) = \lim_{r\rightarrow 0^+} \dfrac{1}{\pi r^2} \int_{C_{\tau}} \vecs F \cdot d\vecs r. \nonumber \]
This equation relates the curl of a vector field to the circulation. Since the area of the disk is \(\pi r^2\), this equation says we can view the curl (in the limit) as the circulation per unit area. Recall that if \(\vecs F\) is the velocity field of a fluid, then circulation \[\oint_{C_{\tau}} \vecs F \cdot d\vecs r = \oint_{C_{\tau}} \vecs F \cdot \vecs T \, ds \nonumber \] is a measure of the tendency of the fluid to move around \(C_{\tau}\): The reason for this is that \(\vecs F \cdot \vecs T\) is a component of \(\vecs F\) in the direction of \(\vecs T\), and the closer the direction of \(\vecs F\) is to \(\vecs T\), the larger the value of \(\vecs F \cdot \vecs T\) (remember that if \(\vecs a\) and \(\vecs b\) are vectors and \(\vecs b\) is fixed, then the dot product \(\vecs a \cdot \vecs b\) is maximal when \(\vecs a\) points in the same direction as \(\vecs b\)). Therefore, if \(\vecs F\) is the velocity field of a fluid, then \(curl \, \vecs F \cdot \vecs N\) is a measure of how the fluid rotates about axis \(\vecs N\). The effect of the curl is largest about the axis that points in the direction of \(\vecs N\), because in this case \(curl \, \vecs F \cdot \vecs N\) is as large as possible.
To see this effect in a more concrete fashion, imagine placing a tiny paddlewheel at point \(P_0\) (Figure \(\PageIndex{8}\)). The paddlewheel achieves its maximum speed when the axis of the wheel points in the direction of curl \(\vecs F\). This justifies the interpretation of the curl we have learned: curl is a measure of the rotation in the vector field about the axis that points in the direction of the normal vector \(\vecs N\), and Stokes’ theorem justifies this interpretation.
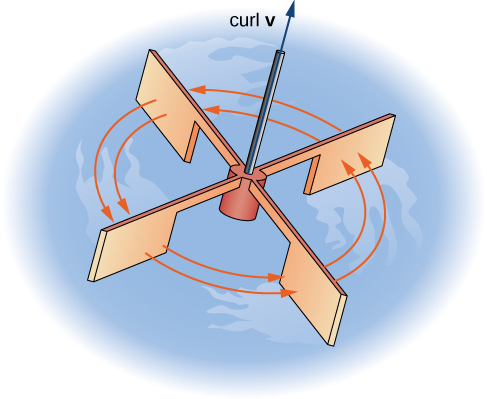
Now that we have learned about Stokes’ theorem, we can discuss applications in the area of electromagnetism. In particular, we examine how we can use Stokes’ theorem to translate between two equivalent forms of Faraday’s law. Before stating the two forms of Faraday’s law, we need some background terminology.
Let \(C\) be a closed curve that models a thin wire. In the context of electric fields, the wire may be moving over time, so we write \(C(t)\) to represent the wire. At a given time \(t\), curve \(C(t)\) may be different from original curve \(C\) because of the movement of the wire, but we assume that \(C(t)\) is a closed curve for all times \(t\). Let \(D(t)\) be a surface with \(C(t)\) as its boundary, and orient \(C(t)\) so that \(D(t)\) has positive orientation. Suppose that \(C(t)\)is in a magnetic field \(\vecs B(t)\) that can also change over time. In other words, \(\vecs{B}\) has the form
\[\vecs B(x,y,z) = \langle P(x,y,z), \, Q(x,y,z), \, R(x,y,z) \rangle, \nonumber \]
where \(P\), \(Q\), and \(R\) can all vary continuously over time. We can produce current along the wire by changing field \(\vecs B(t)\) (this is a consequence of Ampere’s law). Flux \(\displaystyle \phi (t) = \iint_{D(t)} \vecs B(t) \cdot d\vecs S\) creates electric field \(\vecs E(t)\) that does work. The integral form of Faraday’s law states that
\[Work = \int_{C(t)} \vecs E(t) \cdot d\vecs r = - \dfrac{\partial \phi}{\partial t}. \nonumber \]
In other words, the work done by \(\vecs{E}\) is the line integral around the boundary, which is also equal to the rate of change of the flux with respect to time. The differential form of Faraday’s law states that
\[curl \, \vecs{E} = - \dfrac{\partial \vecs B}{\partial t}. \nonumber \]
Using Stokes’ theorem, we can show that the differential form of Faraday’s law is a consequence of the integral form. By Stokes’ theorem, we can convert the line integral in the integral form into surface integral
\[-\dfrac{\partial \phi}{\partial t} = \int_{C(t)} \vecs E(t) \cdot d\vecs r = \iint_{D(t)} curl \,\vecs E(t) \cdot d\vecs S. \nonumber \]
Since \[\phi (t) = \iint_{D(t)} B(t) \cdot d\vecs S, \nonumber \] then as long as the integration of the surface does not vary with time we also have
\[- \dfrac{\partial \phi}{\partial t} = \iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S. \nonumber \]
Therefore,
\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S. \nonumber \]
To derive the differential form of Faraday’s law, we would like to conclude that \(curl \,\vecs E = -\dfrac{\partial \vecs B}{\partial t}\): In general, the equation
\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S \nonumber \]
is not enough to conclude that \(curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}\): The integral symbols do not simply “cancel out,” leaving equality of the integrands. To see why the integral symbol does not just cancel out in general, consider the two single-variable integrals \(\displaystyle \int_0^1 x \, dx\) and \(\displaystyle \int_0^1 f(x)\, dx\), where
\[f(x) = \begin{cases}1, &\text{if } 0 \leq x \leq 1/2 \\ 0, & \text{if } 1/2 \leq x \leq 1. \end{cases} \nonumber \]
Both of these integrals equal \(\dfrac{1}{2}\), so \(\displaystyle \int_0^1 x \, dx = \int_0^1 f(x) \, dx\).
However, \(x \neq f(x)\). Analogously, with our equation \[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S, \nonumber \] we cannot simply conclude that \(curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}\) just because their integrals are equal. However, in our context, equation
\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S \nonumber \]
is true for any region, however small (this is in contrast to the single-variable integrals just discussed). If \(\vecs F\) and \(\vecs G\) are three-dimensional vector fields such that
\[\iint_S \vecs F \cdot d\vecs S = \iint_S \vecs G \cdot d\vecs S \nonumber \]
for any surface \(S\), then it is possible to show that \(\vecs F = \vecs G\) by shrinking the area of \(S\) to zero by taking a limit (the smaller the area of \(S\), the closer the value of \(\displaystyle \iint_S \vecs F \cdot d\vecs S\) to the value of \(\vecs F\) at a point inside \(S\)). Therefore, we can let area \(D(t)\) shrink to zero by taking a limit and obtain the differential form of Faraday’s law:
\[curl \,\vecs E = - \dfrac{\partial \vecs B}{\partial t}. \nonumber \]
In the context of electric fields, the curl of the electric field can be interpreted as the negative of the rate of change of the corresponding magnetic field with respect to time.
Calculate the curl of electric field \(\vecs{E}\) if the corresponding magnetic field is constant field \(\vecs B(t) = \langle 1, -4, 2 \rangle\).
Solution
Since the magnetic field does not change with respect to time, \(-\dfrac{\partial \vecs B}{\partial t} = \vecs 0\). By Faraday’s law, the curl of the electric field is therefore also zero.
AnalysisA consequence of Faraday’s law is that the curl of the electric field corresponding to a constant magnetic field is always zero.
Calculate the curl of electric field \(\vecs{E}\) if the corresponding magnetic field is \(\vecs B(t) = \langle tx, \, ty, \, -2tz \rangle, \, 0 \leq t < \infty.\)
- Hint
-
- Use the differential form of Faraday’s law.
- Notice that the curl of the electric field does not change over time, although the magnetic field does change over time.
- Answer
-
\(curl \, \vecs{E} = \langle x, \, y, \, -2z \rangle\)
Key Concepts
- Stokes’ theorem relates a flux integral over a surface to a line integral around the boundary of the surface. Stokes’ theorem is a higher dimensional version of Green’s theorem, and therefore is another version of the Fundamental Theorem of Calculus in higher dimensions.
- Stokes’ theorem can be used to transform a difficult surface integral into an easier line integral, or a difficult line integral into an easier surface integral.
- Through Stokes’ theorem, line integrals can be evaluated using the simplest surface with boundary \(C\).
- Faraday’s law relates the curl of an electric field to the rate of change of the corresponding magnetic field. Stokes’ theorem can be used to derive Faraday’s law.
Key Equations
- Stokes’ theorem
\[\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]
Glossary
- Stokes’ theorem
- relates the flux integral over a surface \(S\) to a line integral around the boundary \(C\) of the surface \(S\)
- surface independent
- flux integrals of curl vector fields are surface independent if their evaluation does not depend on the surface but only on the boundary of the surface



Appliquer le théorème de Stokes
Le théorème de Stokes traduit entre l'intégrale de flux de la surface\(S\) en une intégrale de droite autour de la limite de\(S\). Par conséquent, le théorème nous permet de calculer des intégrales de surface ou des intégrales de lignes qui seraient normalement assez difficiles en traduisant l'intégrale de la droite en une intégrale de surface ou vice versa. Nous étudions maintenant quelques exemples de chaque type de traduction.
Exemple\(\PageIndex{2}\): Calculating a Surface Integral
Calculer l'intégrale de
\[\iint_S curl \, \vecs{F} \cdot d\vecs S, \nonumber \]
où\(S\) est la surface, orientée vers l'extérieur, sur les figures\(\PageIndex{6}\) et\(\vecs{F} = \langle z,\, 2xy, \, x + y \rangle\).
Solution
Notez que pour calculer
\[ \iint_S curl \, \vecs F \cdot d\vecs S \nonumber \]
sans utiliser le théorème de Stokes, nous aurions besoin de l'équation pour les intégrales de surface scalaires. L'utilisation de cette équation nécessite un paramétrage de\(S\). \(S\)La surface est suffisamment compliquée pour qu'il soit extrêmement difficile de trouver un paramétrage. Par conséquent, les méthodes que nous avons apprises dans les sections précédentes ne sont pas utiles pour ce problème. Nous utilisons plutôt le théorème de Stokes, en notant que la limite\(C\) de la surface est simplement un cercle unique de rayon 1.
La boucle de\(\vecs{F}\) nous\(\langle 1,1,2y \rangle\). Selon le théorème de Stokes,
\[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r, \nonumber \]
où\(C\) a un paramétrage\(\langle \cos t, \, \sin t, \, 1 \rangle, 0 \leq t \leq 2\pi\). Par l'équation des intégrales de lignes vectorielles,
\[ \begin{align*} \iint_S curl \, F \cdot d\vecs S &= \int_C \vecs{F} \cdot d \vecs{r} \\[4pt] &= \int_0^2 \langle 1, \, \sin t \, \cos t, \, \cos t + \sin t \rangle \cdot \langle - \sin t, \, \cos t, \, 0 \rangle \, dt \\[4pt] &= \int_0^{2\pi} ( - \sin t + 2 \, \sin t \, \cos^2 t ) \, dt \\[4pt] &= \left[ \cos t - \dfrac{2 \, \cos^3 t}{3} \right]_0^{2\pi} \\[4pt] &= \cos (2\pi) - \dfrac{2 \, \cos^3 (2\pi)}{3} - \left(\cos (0) - \dfrac{2 \, \cos^3 (0)}{3} \right) \\[4pt] &= 0. \end{align*} \nonumber \]
Une conséquence étonnante du théorème de Stokes est qu'il s'\(S'\)agit d'une autre surface lisse ayant une limite\(C\) et la même orientation que\(S\), alors\[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = 0 \nonumber \] parce que le théorème de Stokes dit que l'intégrale de surface dépend de l'intégrale de la ligne autour de la limite uniquement.
Dans Exemple\(\PageIndex{2}\), nous avons calculé une intégrale de surface simplement en utilisant des informations sur la limite de la surface. En général, laissez\(S_1\) et\(S_2\) soyez des surfaces lisses avec la même limite\(C\) et la même orientation. Selon le théorème de Stokes,
\[\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} = \int_C \vecs{F} \cdot d\vecs{r} = \iint_{S_2} curl \, \vecs{F} \cdot d\vecs{S}. \label{20} \]
Par conséquent, si
\[\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]
est difficile à calculer mais
\[\iint_{S_2} curl \, \vecs{F} \cdot d\vecs S \nonumber \]
est facile à calculer, le théorème de Stokes nous permet de calculer l'intégrale de surface la plus facile. Dans l'exemple\(\PageIndex{2}\), nous aurions pu calculer
\[\iint_S curl \, \vecs{F} \cdot d \vecs{S} \nonumber \]
en calculant
\[\iint_{S'} curl \, \vecs{F} \cdot d\vecs{S}, \nonumber \]
où se\(\vecs{S}'\) trouve le disque entouré d'une courbe limite\(C\) (une surface beaucoup plus simple avec laquelle travailler).
L'équation \ ref {20} montre que les intégrales de flux des champs vectoriels de courbure sont indépendantes de la surface, de la même manière que les intégrales linéaires des champs de gradient sont indépendantes de la trajectoire. Rappelez-vous que s'il s'\(\vecs{F}\)agit d'un champ vectoriel conservateur bidimensionnel défini sur un domaine simplement connecté,\(f\) s'il s'agit d'une fonction potentielle pour\(\vecs{F}\) et\(C\) d'une courbe dans le domaine de\(\vecs{F}\), alors
\[\int_C \vecs{F} \cdot d\vecs{r} \nonumber \]
dépend uniquement des points de terminaison de\(C\). Par conséquent, s'il s'\(C'\)agit d'une autre courbe ayant le même point de départ et la même extrémité que\(C\) (c'est-à-dire qu'\(C'\)elle a la même orientation que\(C\)), alors
\[\int_C \vecs{F} \cdot d\vecs{r} = \int_{C'} \vecs{F} \cdot d\vecs{r} \nonumber \]
En d'autres termes, la valeur de l'intégrale dépend uniquement de la limite du chemin ; elle ne dépend pas vraiment du chemin lui-même.
De même, supposons que\(S\) et\(S'\) soient des surfaces ayant la même limite et la même orientation, et supposons qu'il\(\vecs{G}\) s'agit d'un champ vectoriel tridimensionnel qui peut être écrit comme la courbure d'un autre champ vectoriel\(\vecs{F}\) (\(\vecs{F}\)c'est-à-dire comme un « champ potentiel » de\(\vecs{G}\)). Par équation \ ref {20},
\[ \begin{align*} \iint_S \vecs G \cdot d\vecs S = \iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = \iint_{S'} curl \, \vecs F \cdot d\vecs S = \iint_{S'} \vecs G \cdot d\vecs S.\end{align*} \nonumber \]
Par conséquent, l'intégrale de flux de\(\vecs{G}\) ne dépend pas de la surface, mais uniquement de la limite de la surface. Les intégrales de flux des champs vectoriels qui peuvent être écrites sous la forme de la courbure d'un champ vectoriel sont indépendantes de la surface, de la même manière que les intégrales linéaires des champs vectoriels qui peuvent être écrites sous la forme du gradient d'une fonction scalaire sont indépendantes du chemin.
Exercice\(\PageIndex{1}\)
Utilisez le théorème de Stokes pour calculer l'intégrale de surface\[\iint_S curl \, \vecs{F} \cdot d\vecs{S}, \nonumber \] où\(\vecs{F} = \langle x,y,z \rangle\) et\(S\) est la surface, comme indiqué dans la figure suivante.
Paramétrer la limite de\(S\) and translate to a line integral.
\(-\pi\)