Skip to main content
Global

11.3E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194484

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique rend la perfection

    Exercice\(\PageIndex{17}\) Graph Vertical Parabolas

    Dans les exercices suivants, tracez chaque équation à l'aide de propriétés.

    1. \(y=-x^{2}+4 x-3\)
    2. \(y=-x^{2}+8 x-15\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(y=8 x^{2}-10 x+3\)
    Réponse

    1.

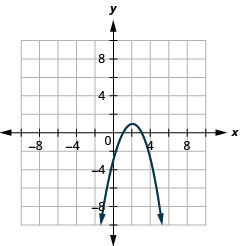
    Ce graphique montre une parabole s'ouvrant vers le bas avec des sommets (2, 1) et des points d'intersection x (1, 0) et (3, 0).
    Graphique 11.2.83

    3.

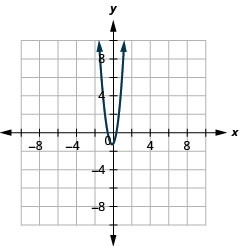
    Ce graphique montre une parabole s'ouvrant vers le haut. Le sommet est (négatif 0,167, négatif 1,167), les interceptions x sont (négatif 0,608) et (négatif 0,274, 0), et l'intersection y est (0, négatif 1).
    Graphique 11.2.84
    Exercice\(\PageIndex{18}\) Graph Vertical Parabolas

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard et
    2. Utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.
    1. \(y=-x^{2}+2 x-4\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(y=-2 x^{2}-4 x-5\)
    4. \(y=3 x^{2}-12 x+7\)
    Réponse

    1.

    1. \(y=-(x-1)^{2}-3\)
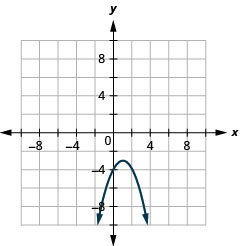
    Ce graphique montre une parabole s'ouvrant vers le bas avec un sommet (1, négatif 3) et une intersection y (0, 4).
    Graphique 11.2.85

    3.

    1. \(y=-2(x+1)^{2}-3\)
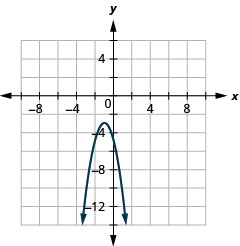
    Ce graphique montre une parabole s'ouvrant vers le bas avec des sommets (négatif 1, négatif 3) et des points d'intersection x (négatif 5, 0).
    Graphique 11.2.86
    Exercice\(\PageIndex{19}\) Graph Horizontal Parabolas

    Dans les exercices suivants, tracez chaque équation à l'aide de propriétés.

    1. \(x=-2 y^{2}\)
    2. \(x=3 y^{2}\)
    3. \(x=4 y^{2}\)
    4. \(x=-4 y^{2}\)
    5. \(x=-y^{2}-2 y+3\)
    6. \(x=-y^{2}-4 y+5\)
    7. \(x=y^{2}+6 y+8\)
    8. \(x=y^{2}-4 y-12\)
    9. \(x=(y-2)^{2}+3\)
    10. \(x=(y-1)^{2}+4\)
    11. \(x=-(y-1)^{2}+2\)
    12. \(x=-(y-4)^{2}+3\)
    13. \(x=(y+2)^{2}+1\)
    14. \(x=(y+1)^{2}+2\)
    15. \(x=-(y+3)^{2}+2\)
    16. \(x=-(y+4)^{2}+3\)
    17. \(x=-3(y-2)^{2}+3\)
    18. \(x=-2(y-1)^{2}+2\)
    19. \(x=4(y+1)^{2}-4\)
    20. \(x=2(y+4)^{2}-2\)
    Réponse

    1.

    Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (0, 0). Deux points sont (négatif 2, 1) et (négatif 2, négatif 1).
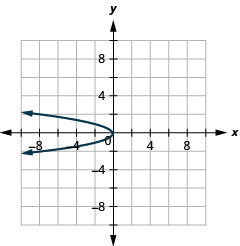
    Graphique 11.2.87

    3.

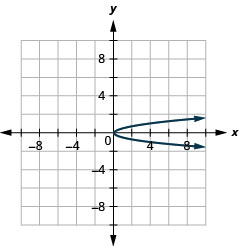
    Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (0, 0). Deux points sont (4, 1) et (4, négatif 1).
    Graphique 11.2.88

    5.

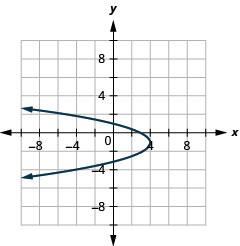
    Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (4, négatif 1) et des intersections y (0, 1) et (0, négatif 3).
    Graphique 11.2.89

    7.

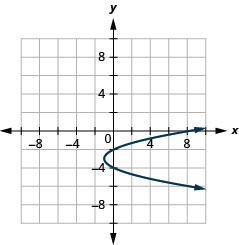
    Ce graphique montre une parabole s'ouvrant vers la droite avec des sommets (négatif 1, moins 3) et des intersections y (0, négatif 2) et (0, négatif 4).
    Graphique 11.2.90

    9.

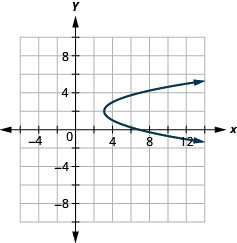
    Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (3, 2) et une intersection en x (7, 0).
    Graphique 11.2.91

    11.

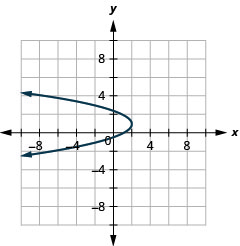
    Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (2, 1) et une intersection en x (1, 0).
    Graphique 11.2.92

    13.

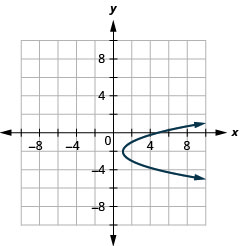
    Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (1, négatif 2) et une intersection en x (5, 0).
    Graphique 11.2.93

    15.

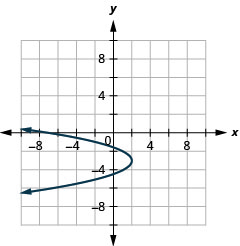
    Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (2, négatif 3). Deux points sont (négatif 2, négatif 1) et (négatif 2, 5).
    Graphique 11.2.94

    17.

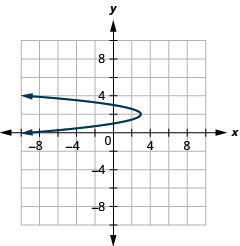
    Ce graphique montre une parabole s'ouvrant vers la gauche avec des sommets (3, 2) et des intersections y (0, 1) et (0, 3).
    Graphique 11.2.95

    19.

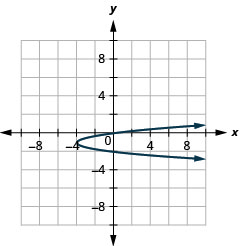
    Ce graphique montre une parabole s'ouvrant vers la droite avec des sommets (négatif 4, négatif 1) et des intersections y (0, 0) et (0, négatif 2).
    Graphique 11.2.96
    Exercice\(\PageIndex{20}\) Graph Horizontal Parabolas

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard et
    2. Utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.
    1. \(x=y^{2}+4 y-5\)
    2. \(x=y^{2}+2 y-3\)
    3. \(x=-2 y^{2}-12 y-16\)
    4. \(x=-3 y^{2}-6 y-5\)
    Réponse

    1.

    1. \(x=(y+2)^{2}-9\)
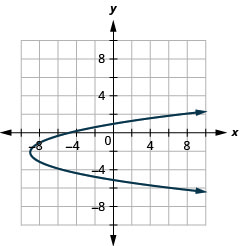
    Ce graphique montre une parabole s'ouvrant vers la droite avec des sommets (négatif 9, négatif 2) et des intersections y (0, 1) et (0, négatif 5).
    Graphique 11.2.97

    3.

    1. \(x=-2(y+3)^{2}+2\)
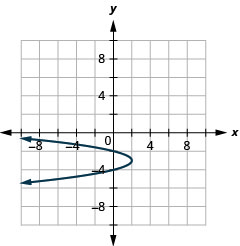
    Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (2, moins 3) et des intersections y (0, moins 2) et (0, moins 4).
    Graphique 11.2.98
    Exercice\(\PageIndex{21}\) Mixed Practice

    Dans les exercices suivants, associez chaque graphique à l'une des équations suivantes :

    1. \(x^{2}+y^{2}=64\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \((x-2)^{2}+(y-3)^{2}=9\)
    5. \(y=-x^{2}+8 x-15\)
    6. \(y=6 x^{2}+2 x-1\)

    1.

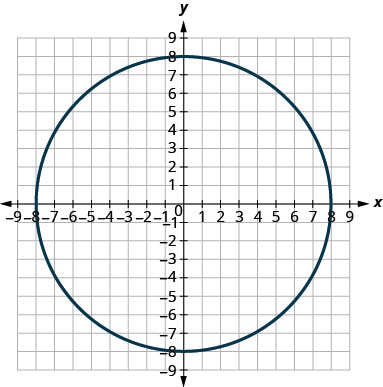
    Ce graphique montre un cercle avec un centre (0, 0) et un rayon de 8 unités.
    Graphique 11.2.99

    2.

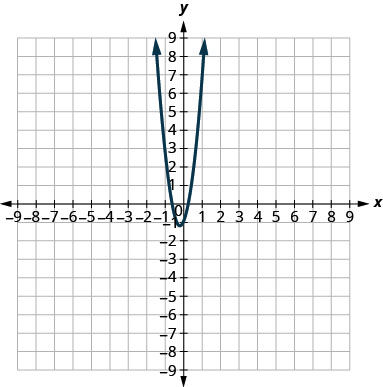
    Ce graphique montre une parabole s'ouvrant vers le haut. Son sommet a une valeur x légèrement inférieure à 0 et une valeur y légèrement inférieure à moins 1. Un point sur ce point est proche de (négatif 1, 3).
    Figure 11.2.100

    3.

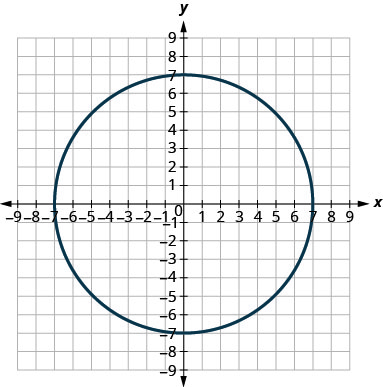
    Ce graphique montre un cercle avec un centre (0, 0) et un rayon de 7 unités.
    Figure 11.2.101

    4.

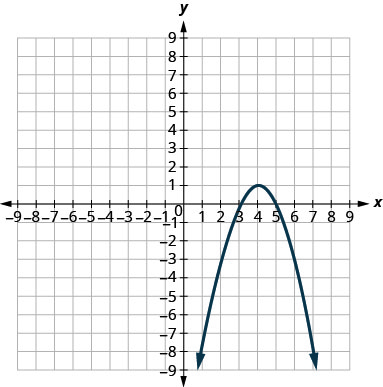
    Ce graphique montre une parabole s'ouvrant vers le bas avec un sommet (4, 1) et des points d'intersection x (3, 0) et (5, 0).
    Figure 11.2.102

    5.

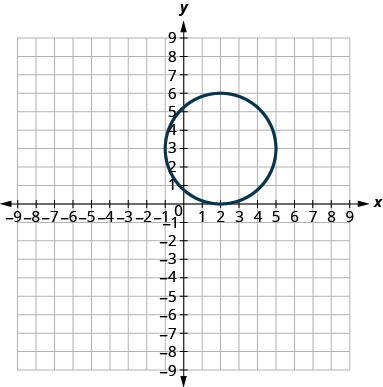
    Ce graphique montre un cercle avec un centre (2, 3) et un rayon de 3 unités.
    Figure 11.2.103

    6.

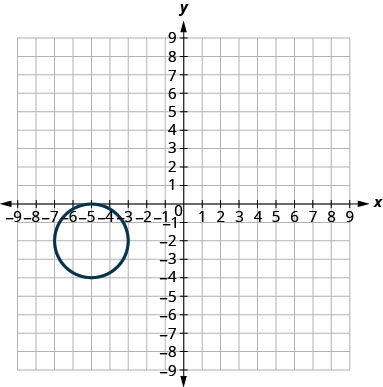
    Ce graphique montre un cercle avec un centre (moins 5, moins 2) et un rayon de 2 unités.
    Figure 11.2.104
    Réponse

    1. une

    3,0 b

    5. d

    Exercice\(\PageIndex{22}\) Solve Applications with Parabolas

    Écrivez l'équation sous forme standard de l'arc parabolique formé dans la fondation du pont illustré. Utilisez le côté inférieur gauche du pont comme point d'origine\((0, 0)\).

    1.

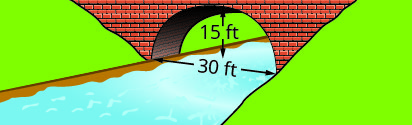
    Ce graphique montre un cercle avec un centre (moins 5, moins 2) et un rayon de 2 unités.
    Figure 11.2.105

    2.

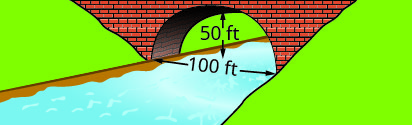
    Cette figure montre un arc parabolique formé dans les fondations d'un pont. Il mesure 50 pieds de haut et 100 pieds de large à la base.
    Figure 11.2.106

    3.

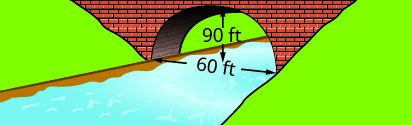
    Cette figure montre un arc parabolique formé dans les fondations d'un pont. Il mesure 90 pieds de haut et 60 pieds de large à la base.
    Figure 11.2.107

    4.

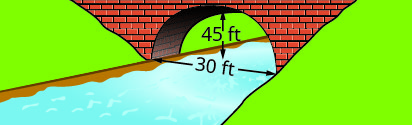
    Cette figure montre un arc parabolique formé dans les fondations d'un pont. Il mesure 45 pieds de haut et 30 pieds de large à la base.
    Figure 11.2.108
    Réponse

    1. \(y=-\frac{1}{15}(x-15)^{2}+15\)

    3. \(y=-\frac{1}{10}(x-30)^{2}+90\)

    Exercice\(\PageIndex{23}\) Writing Exercises
    1. Définissez une parabole avec vos propres mots.
    2. La parabole est-elle\(y=x^{2}\) une fonction ? La parabole est-elle\(x=y^{2}\) une fonction ? Expliquez pourquoi ou pourquoi pas.
    3. Écrivez l'équation d'une parabole qui s'ouvre vers le haut ou vers le bas sous forme standard et l'équation d'une parabole qui s'ouvre vers la gauche ou la droite sous forme standard. Fournissez une esquisse de la parabole pour chacune d'elles, étiquetez le sommet et l'axe de symétrie.
    4. Expliquez avec vos propres mots comment vous pouvez déterminer à partir de son équation si une parabole s'ouvre vers le haut, vers le bas, vers la gauche ou vers la droite.
    Réponse

    1. Les réponses peuvent varier

    3. Les réponses peuvent varier

    Auto-vérification

    a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

    Ce tableau comporte quatre colonnes, trois rangées et une ligne d'en-tête. La ligne d'en-tête étiquette chaque colonne que je peux, en toute confiance, avec de l'aide et non, je ne comprends pas.™ La première colonne contient les déclarations suivantes : tracez des paraboles verticales, tracez des paraboles horizontales, résolvez des applications avec des paraboles. Les colonnes restantes sont vides.
    Figure 11.2.109

    b. Après avoir examiné cette liste de contrôle, que ferez-vous pour atteindre tous les objectifs en toute confiance ?