Skip to main content
Global

11.4 : Ellipses

  1. Last updated
  2. Save as PDF
  • Page ID
    194532

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Tracez une ellipse dont le centre se trouve à l'origine
    • Trouvez l'équation d'une ellipse dont le centre est l'origine
    • Tracez une ellipse dont le centre n'est pas à l'origine
    • Résoudre une application avec des ellipses

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Graphe\(y=(x-1)^{2}-2\) utilisant des transformations.
      Si vous avez oublié ce problème, consultez l'exemple 9.57.
    2. Complétez le carré :\(x^{2}-8 x=8\).
      Si vous avez oublié ce problème, consultez l'exemple 9.12.
    3. Écrivez sous forme standard. \(y=2 x^{2}-12 x+14\)
      Si vous avez oublié ce problème, consultez l'exemple 9.59.

    Tracez une ellipse dont le centre est à l'origine

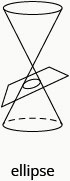
    La prochaine section conique que nous allons examiner est une ellipse. Nous définissons une ellipse comme l'ensemble des points d'un plan où la somme des distances entre deux points fixes est constante. Chacun des points donnés est appelé foyer de l'ellipse.

    Définition\(\PageIndex{1}\)

    Une ellipse est constituée de tous les points d'un plan où la somme des distances entre deux points fixes est constante. Chacun des points fixes est appelé foyer de l'ellipse.

    Cette figure montre un double cône croisé par un plan pour former une ellipse.
    Graphique 11.3.1

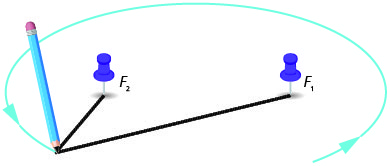
    Nous pouvons dessiner une ellipse en prenant une corde flexible d'une longueur fixe et en attachant les extrémités à deux punaises. Nous utilisons un stylo pour tendre la ficelle et la faire pivoter autour des deux punaises. La figure qui en résulte est une ellipse.

    Cette figure montre un stylo attaché à deux cordes dont les autres extrémités sont attachées à deux punaises. Les cordes sont tendues et le stylo pivote pour dessiner une ellipse. Les punaises sont étiquetées F indice 1 et indice F 2.
    Graphique 11.3.2

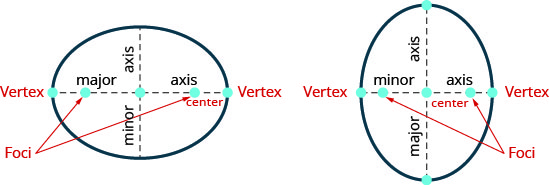
    Une ligne tracée à travers les foyers coupe l'ellipse en deux points. Chaque point est appelé sommet de l'ellipse. Le segment reliant les sommets est appelé axe principal. Le milieu du segment est appelé le centre de l'ellipse. Un segment perpendiculaire à l'axe principal qui passe par le centre et coupe l'ellipse en deux points est appelé axe secondaire.

    Cette figure montre deux ellipses. Dans chacun d'eux, deux points de l'ellipse sont appelés foyers. Une ligne tracée à travers les foyers coupe l'ellipse en deux points. Chaque point est étiqueté sommet. Dans la figure de gauche, le segment reliant les sommets est appelé axe principal. Un segment perpendiculaire à l'axe principal qui passe par son point médian et coupe l'ellipse en deux points est appelé axe secondaire. L'axe principal est plus long que l'axe secondaire. Dans la figure de droite, le segment passant par les foyers, reliant les sommets est plus court et est étiqueté axe mineur. Son point médian est étiqueté centre.
    Graphique 11.3.3

    Nous avons mentionné précédemment que notre objectif est de relier la géométrie d'une conique à l'algèbre. Le fait de placer l'ellipse sur un système de coordonnées rectangulaires nous donne cette opportunité. Sur la figure, nous avons placé l'ellipse de manière à ce que\(((−c,0),(c,0))\) les foyers soient sur l'\(x\)axe -et que le centre soit l'origine.

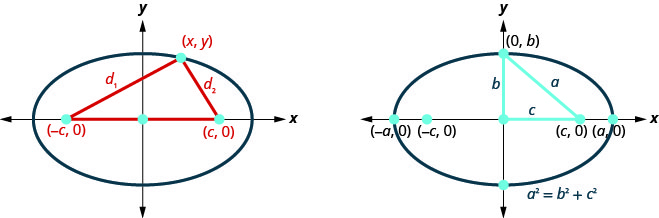
    La figure de gauche montre une ellipse dont le centre se trouve à l'origine des axes de coordonnées et dont les foyers se situent aux points moins (c, 0) et (c, 0). Un segment est connecté (négatif c, 0) à un point (x, y) de l'ellipse. Le segment est étiqueté en indice 1. Un autre segment, nommé d indice 2, relie (c, 0) à (x, y). La figure de droite montre une ellipse dont le centre est à l'origine, des foyers (négatif c, 0) et (c, 0) et des sommets (négatif a, 0) et (a, 0). Le point où l'ellipse croise l'axe y est étiqueté (0, b). Les segments reliant (0, 0) à (c, 0), (c, 0) à (0, b) et (0, b) à (0, 0) forment un triangle à angle serré avec les côtés c, a et b respectivement. L'équation est la suivante : a au carré est égal à b au carré plus c au carré.
    Graphique 11.3.4

    La définition indique que la somme de la distance entre les foyers et un point\((x,y)\) est constante. \(d_{1}+d_{2}\)Il en va de même pour une constante que nous appellerons\(2a\) ainsi\(d_{1}+d_{2}=2 a\). Nous utiliserons la formule de distance pour nous amener à une formule algébrique pour une ellipse.

    \(d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a\)

    Utilisez la formule de distance pour trouver\(d_{1},d_{2}\).

    \(\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a\)

    Après avoir éliminé les radicaux et simplifié, on obtient :

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1\)

    Pour simplifier l'équation de l'ellipse, nous utilisons\(a^{2}−c^{2}=b^{2}\). Ainsi, l'équation d'une ellipse centrée à l'origine sous forme standard est la suivante :

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Pour représenter graphiquement l'ellipse, il sera utile de connaître les interceptions. Nous trouverons les\(x\) -intercepts et\(y\) -intercepts en utilisant la formule.

    \(y\)-intercepte

    Laissez\(x=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}\)

    Les\(y\) -intercepts sont\((0,b)\) et\((0, -b)\).

    \(x\)-intercepte

    Laissez\(y=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)

    Les\(x\) -intercepts sont\((a,0)\) et\((-a,0)\).

    Définition\(\PageIndex{2}\)

    Forme standard de l'équation : une ellipse avec un centre\((0,0)\)

    La forme standard de l'équation d'une ellipse avec centre\((0,​​0)\) est

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Les\(x\) -intercepts sont\((a,0)\) et\((−a,0)\).

    Les\(y\) -intercepts sont\((0,b)\) et\((0,−b)\).

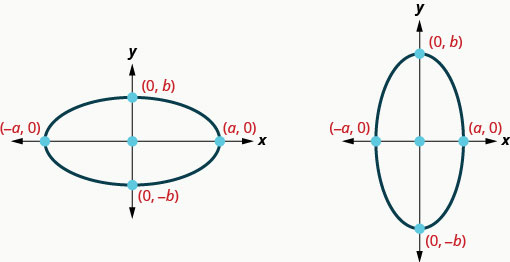
    Deux figures montrent des ellipses dont le centre se trouve à l'origine des axes de coordonnées. Ils coupent l'axe x aux points (négatif a, 0) et (a, 0) et l'axe y aux points (0, b) et (0, négatif b). Dans la figure de gauche, le grand axe de l'ellipse se trouve le long de l'axe x et dans la figure de droite, il se trouve le long de l'axe y.
    Graphique 11.3.5

    Notez que lorsque l'axe principal est horizontal, la valeur de\(a\) sera supérieure à la valeur de\(b\) et lorsque l'axe principal est vertical, la valeur de\(b\) sera supérieure à la valeur de\(a\). Nous utiliserons ces informations pour tracer une ellipse centrée à l'origine.

    Ellipse avec centre\((0,0)\)

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) \(a>b\) \(b>a\)
    Axe principal sur l'\(x\)axe. sur l'\(y\)axe -
    \(x\)-intercepte \((-a, 0),(a, 0)\)  
    \(y\)-intercepte \((0,-b),(0, b)\)  
    Tableau 11.3.1
    Exemple\(\PageIndex{1}\)

    Graphique :\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).

    Solution :

    Étape 1. Écrivez l'équation sous forme standard. Il se présente sous une forme standard. \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)
    Étape 2. Déterminez si l'axe principal est horizontal ou vertical. Puisque\(9>4\) et\(9\) est dans le\(y^{2}\) terme, l'axe principal est vertical. L'axe principal est vertical.
    Étape 3. Trouvez les extrémités de l'axe principal.

    Les points de terminaison seront les\(y\) -intercepts.

    Depuis\(b^{2}=9\), alors\(b=\pm 3\).

    Les points d'extrémité de l'axe principal sont\((0,3),(0,-3)\).

    		 Les points d'extrémité de l'axe principal sont\((0,3),(0,-3)\).
    Étape 4. Trouvez les extrémités de l'axe secondaire. Les points de terminaison seront les\(x\) -intercepts.

    Depuis\(a^{2}=4\), alors\(a=\pm 2\).

    Les points d'extrémité de l'axe principal sont\((2,0),(-2,0)\).

    		 Les points d'extrémité de l'axe principal sont\((2,0),(-2,0)\).
    Étape 5. Esquissez l'ellipse.   Capture d'écran (147) .png
    Tableau 11.3.2
    Exercice\(\PageIndex{1}\)

    Graphique :\(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\).

    Réponse
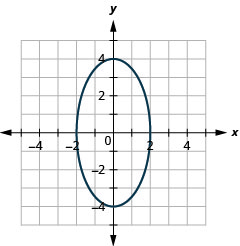
    Ce graphique montre une ellipse avec x interceptions (moins 2, 0) et (2, 0) et y interceptions (0, 4) et (0, moins 4).
    Graphique 11.3.7
    Exercice\(\PageIndex{2}\)

    Graphique :\(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\).

    Réponse
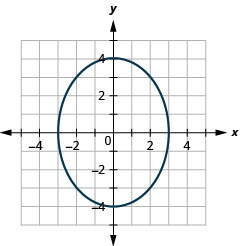
    Ce graphique montre une ellipse avec x interceptions (moins 3, 0) et (3, 0) et y interceptions (0, 4) et (0, moins 4).
    Graphique 11.3.8

    Nous résumons les étapes à titre de référence.

    COMMENT REPRÉSENTER GRAPHIQUEMENT UNE ELLIPSE AVEC UN CENTRE\((0,0)\).

    1. Écrivez l'équation sous forme standard.
    2. Déterminez si l'axe principal est horizontal ou vertical.
    3. Trouvez les extrémités de l'axe principal.
    4. Trouvez les extrémités de l'axe secondaire
    5. Esquissez l'ellipse.

    Parfois, notre équation devra d'abord être mise sous forme standard.

    Exemple\(\PageIndex{2}\)

    Graphe\(x^{2}+4 y^{2}=16\).

    Solution :

    Nous reconnaissons qu'il s'agit de l'équation d'une
    ellipse puisque les\(y\) termes\(x\) et sont tous deux
    au carré et ont des coefficients différents.    		 \(x^{2}+4 y^{2}=16\)
    Pour obtenir l'équation sous forme standard, divisez
    les deux côtés par de\(16\) telle sorte que l'équation soit égale
    à\(1\).    		 \(\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}\)
    Simplifiez. \(\frac{x^{2}}{16}+\frac{y^{2}}{4}=1\)
    L'équation se présente sous forme standard.
    L'ellipse est centrée à l'origine.    		 Le centre est\((0,0)\).
    Puisque\(16>4\) et\(16\) est dans le\(x^{2}\) terme,
    l'axe principal est horizontal.    		  
    \(a^{2}=16, a=\pm 4\)
    \(b^{2}=4, \quad b=\pm 2\)
    Les sommets sont\((4,0),(−4,0)\).
    Les extrémités de l'axe secondaire sont
    \((0,2),(0,−2)\).
    Esquissez la parabole. .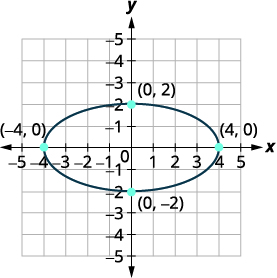
    Tableau 11.3.3
    Exercice\(\PageIndex{3}\)

    Graphe\(9 x^{2}+16 y^{2}=144\).

    Réponse
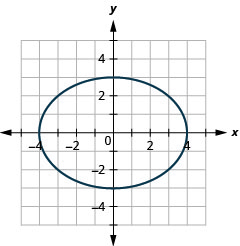
    Ce graphique montre une ellipse avec x interceptions (moins 4, 0) et (4, 0) et y interceptions (0, 3) et (0, moins 3).
    Graphique 11.3.10
    Exercice\(\PageIndex{4}\)

    Graphe\(16 x^{2}+25 y^{2}=400\).

    Réponse
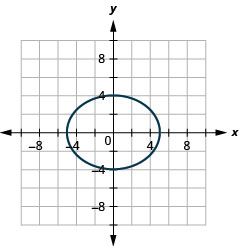
    Ce graphique montre une ellipse avec x interceptions (moins 5, 0) et (5, 0) et y interceptions (0, 4) et (0, moins 4).
    Graphique 11.3.11

    Trouvez l'équation d'une ellipse dont le centre est à l'origine

    Si on nous donne le graphe d'une ellipse, on peut trouver l'équation de l'ellipse.

    Exemple\(\PageIndex{3}\)

    Trouvez l'équation de l'ellipse affichée.

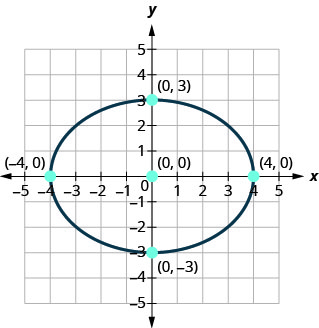
    Ce graphique montre une ellipse avec x interceptions (moins 4, 0) et (4, 0) et y interceptions (0, 3) et (0, moins 3).
    Graphique 11.3.12

    Solution :

    Nous reconnaissons qu'il s'agit d'une ellipse centrée à l'origine.

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Puisque l'axe principal est horizontal et que la distance entre le centre et le sommet l'est\(4\), nous le savons\(a=4\) et ainsi de suite\(a^{2}=16\).

    \(\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1\)

    L'axe secondaire est vertical et la distance entre le centre et l'ellipse est\(3\), nous le savons\(b=3\) et ainsi de suite\(b^{2}=9\).

    \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)

    Exercice\(\PageIndex{5}\)

    Trouvez l'équation de l'ellipse affichée.

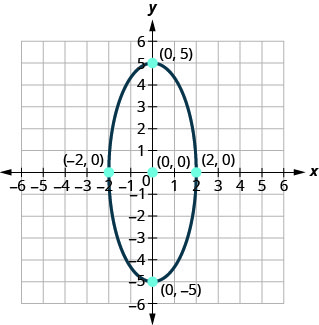
    Ce graphique montre une ellipse avec x interceptions (moins 2, 0) et (2, 0) et y interceptions (0, 5) et (0, moins 5).
    Graphique 11.3.13
    Réponse

    \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)

    Exercice\(\PageIndex{6}\)

    Trouvez l'équation de l'ellipse affichée.

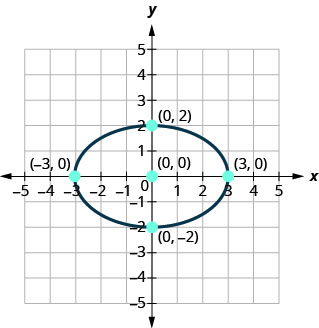
    Ce graphique montre une ellipse avec x interceptions (moins 3, 0) et (3, 0) et y interceptions (0, 2) et (0, moins 2).
    Graphique 11.3.14
    Réponse

    \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)

    Tracez une ellipse dont le centre n'est pas à l'origine

    Les ellipses que nous avons examinées jusqu'à présent étaient toutes centrées à l'origine. Nous allons maintenant examiner les ellipses dont le centre est\((h,k)\).

    L'équation est\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) et quand\(a>b\), l'axe principal est horizontal, donc la distance entre le centre et le sommet est\(a\). Lorsque\(b>a\), l'axe principal est vertical, de sorte que la distance entre le centre et le sommet est de\(b\).

    Définition\(\PageIndex{3}\)

    Forme standard de l'équation : une ellipse avec un centre\((h,k)\)

    La forme standard de l'équation d'une ellipse avec centre\((h,k)\) est

    \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

    Lorsque\(a>b\), l'axe principal est horizontal, de sorte que la distance entre le centre et le sommet est de\(a\).

    Lorsque\(b>a\), l'axe principal est vertical, de sorte que la distance entre le centre et le sommet est de\(b\).

    Exemple\(\PageIndex{4}\)

    Graphique :\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\).

    Solution :

    L'équation est sous forme standard,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\)
    L'ellipse est centrée sur\((h,k)\). Le centre est\((3,1)\).
    Puisque\(9>4\) et\(9\) est dans le\(x^{2}\) terme, l'axe principal est horizontal.  
    \(a^{2}=9, a=\pm 3\)
    \(b^{2}=4, b=\pm 2\)    		 La distance entre le centre et les sommets est de\(3\).
    La distance entre le centre et les extrémités du
    petit axe est de\(2\).
    Esquissez l'ellipse. .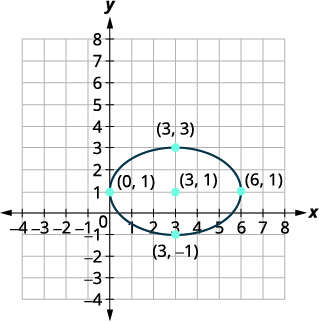
    Tableau 11.3.4
    Exercice\(\PageIndex{7}\)

    Graphique :\(\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1\).

    Réponse
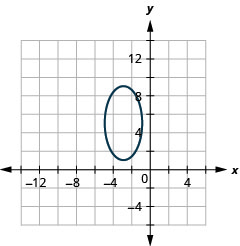
    Ce graphique montre une ellipse dont le centre est à (négatif 3, 5), les sommets à (négatif 3, 9) et (négatif 3, 1) et les extrémités du petit axe à (négatif 5, 5) et (négatif 1, 5).
    Graphique 11.3.16
    Exercice\(\PageIndex{8}\)

    Graphique :\(\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1\).

    Réponse
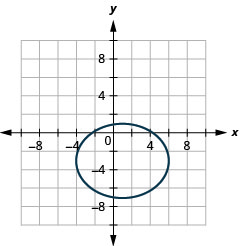
    Ce graphique montre une ellipse dont le centre est à 1, moins 3, les sommets à (moins 4, moins 3) et (6, moins 3) et les extrémités du petit axe à 1, 1) et (négatif 1, moins 7).
    Graphique 11.3.17

    Si nous examinons les équations de\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) et\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\), nous voyons qu'il s'agit toutes deux d'ellipses avec\(a=3\) et\(b=2\). Ils auront donc la même taille et la même forme. Ils sont différents en ce sens qu'ils n'ont pas le même centre.

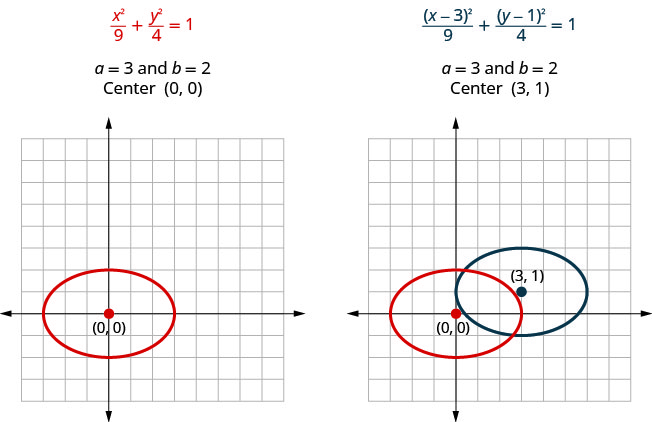
    L'équation de la première figure est x au carré sur 9 plus y au carré sur 4 est égal à 1. Ici, a est 3 et b est 2. L'ellipse est représentée avec le centre à (0, 0). L'équation de droite est la suivante : parenthèses ouvertes x moins 3 parenthèses proches au carré sur 9 plus parenthèses ouvertes y moins 1 parenthèses fermées au carré sur 4 égale 1. Ici aussi, a est 3 et b est 2, mais le centre est (3, 1). L'ellipse est représentée sur le même graphique avec la première ellipse. On montre que le centre a déplacé 3 unités vers la droite et 1 unité vers le haut.
    Graphique 11.3.18

    Remarquez dans le graphique ci-dessus que nous aurions pu représenter graphiquement\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) par traductions. Nous avons déplacé l'ellipse d'origine vers les\(3\) unités de droite, puis l'\(1\)unité vers le haut.

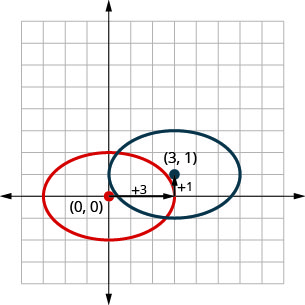
    Ce graphique montre une ellipse translatée du centre (0, 0) au centre (3, 1). Le centre a déplacé 3 unités vers la droite et 1 unité vers le haut. L'ellipse d'origine possède des sommets à (moins 3, 0) et (3, 0) et l'extrémité du petit axe à (moins 2, 0) et (2, 0). L'ellipse translatée possède des sommets à (0, 1) et (6, 1) et des extrémités de l'axe mineur à (3, moins 1) et (3, 3).
    Graphique 11.3.19

    Dans l'exemple suivant, nous utiliserons la méthode de translation pour représenter graphiquement l'ellipse.

    Exemple\(\PageIndex{5}\)

    Graphe\(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) par traduction.

    Solution :

    Cette ellipse aura la même taille et la même forme\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) que son centre\((0,0)\). Nous dessinons d'abord cette ellipse.

    Le centre est\((0,0)\). Centre\((0,0)\)
    Depuis\(16>9\), l'axe principal est horizontal.  
    \(a^{2}=16, a=\pm 4\)
    \(b^{2}=9, \quad b=\pm 3\)    		 Les sommets sont\((4,0),(−4,0)\).
    Les extrémités de l'axe secondaire sont
    \((0,3),(0,−3)\).
    Esquissez l'ellipse. .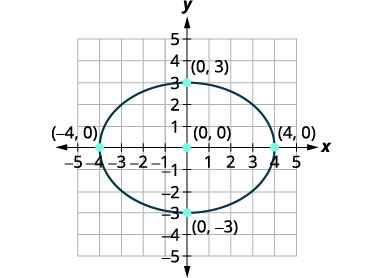
    L'équation d'origine est sous forme standard,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). \(\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1\)
    L'ellipse est centrée sur\((h,k)\). Le centre est\((-4,6)\).
    Nous traduisons le graphique de\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) quatre
    unités vers la gauche, puis vers le haut\(6\).
    Vérifiez que le centre est\((−4,6)\).
    La nouvelle ellipse est l'ellipse dont l'équation
    est
    \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\).    		 .
    Tableau 11.3.5
    Exercice\(\PageIndex{9}\)

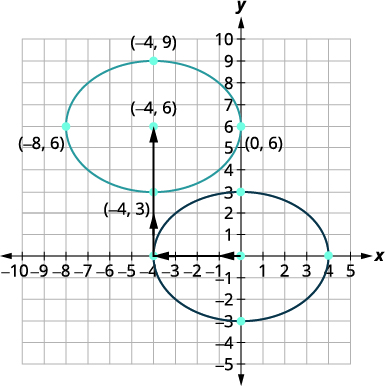    Graphe\(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1\) par traduction.

    Réponse
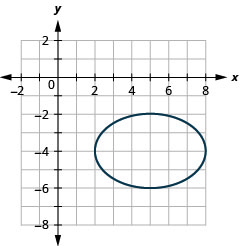
    Ce graphique montre une ellipse avec un centre (5, moins 4), des sommets (2, moins 4) et (8, moins 4) et des extrémités du petit axe (5, moins 2) et (5, moins 6).
    Graphique 11.3.22
    Exercice\(\PageIndex{10}\)

    Graphe\(\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1\) par traduction.

    Réponse
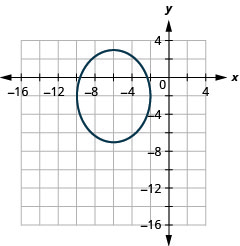
    Ce graphique montre une ellipse avec un centre (négatif 6, moins 2), des sommets (négatif 6, 3) et (négatif 6, moins 7) et des extrémités de l'axe mineur (négatif 10, négatif 2) et (négatif 2, négatif 2).
    Graphique 11.3.23

    Lorsqu'une équation possède à la fois un\(x^{2}\) et un\(y^{2}\) avec des coefficients différents, nous vérifions qu'il s'agit d'une ellipse en la mettant sous forme standard. Nous serons alors en mesure de représenter graphiquement l'équation.

    Exemple\(\PageIndex{6}\)

    Écrivez l'équation\(x^{2}+4 y^{2}-4 x+24 y+24=0\) sous une forme et un graphique standard.

    Solution :

    Nous mettons l'équation sous forme standard en complétant les carrés à la fois dans\(x\) et\(y\).

      \(x^{2}+4 y^{2}-4 x+24 y+24=0\)
    Réécrivez en regroupant les\(x\) termes et les\(y\) termes. .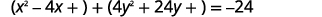
    Faites en sorte que les coefficients\(x^{2}\) soient\(y^{2}\) égaux à\(1\). .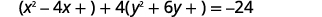
    Complétez les carrés. .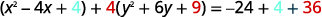
    Écrivez sous forme de carrés binomiaux. .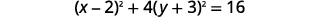
    Divisez les deux côtés\(16\) pour arriver\(1\) sur la droite. .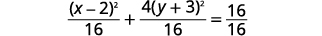
    Simplifiez. .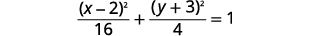
    L'équation est sous forme standard,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) .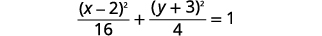
    L'ellipse est centrée sur\((h,k)\). Le centre est\((2,-3)\).

    Puisque\(16>4\) et\(16\) est dans le\(x^{2}\) terme, l'axe principal est horizontal.

    \(a^{2}=16, a=\pm 4\)
    \(b^{2}=4, \quad b=\pm 2\)

    La distance entre le centre et les sommets est de\(4\).

    La distance entre le centre et les extrémités du petit axe est de\(2\).
    Esquissez l'ellipse. .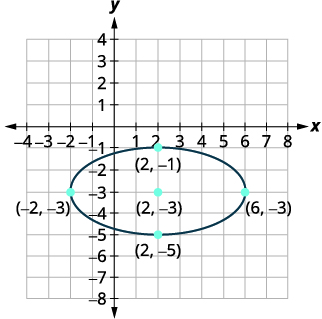
    Tableau 11.3.6
    Exercice\(\PageIndex{11}\)
    1. Écrivez l'équation\(6 x^{2}+4 y^{2}+12 x-32 y+34=0\) sous forme standard et
    2. Graphe.
    Réponse
    1. \(\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1\)
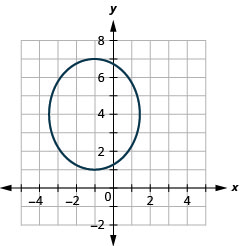
    Ce graphique montre une ellipse avec un centre (moins 1, 4), des sommets moins (1, 1) et (moins 1, 7) et des extrémités du petit axe approximativement (moins 3,5, 4) et (environ 1,5, 4).
    Graphique 11.3.32
    Exercice\(\PageIndex{12}\)
    1. Écrivez l'équation\(4 x^{2}+y^{2}-16 x-6 y+9=0\) sous forme standard et
    2. Graphe.
    Réponse
    1. \(\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1\)
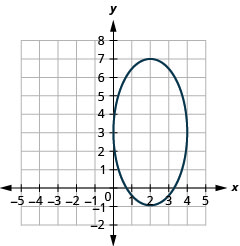
    Ce graphique montre une ellipse avec un centre (2, 3), des sommets (2, négatif 1) et (2, 7) et des extrémités d'un axe mineur (0, 3) et (4, 3).
    Graphique 11.3.3

    Résoudre une application avec des ellipses

    Les orbites des planètes autour du soleil suivent des trajectoires elliptiques.

    Exemple\(\PageIndex{7}\)

    Pluton (une planète naine) se déplace sur une orbite elliptique autour du Soleil. La distance la plus proche entre Pluton et le Soleil est approximativement en unités\(30\) astronomiques (UA) et la plus éloignée est approximativement en\(50\) UA. Le Soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de Pluton.

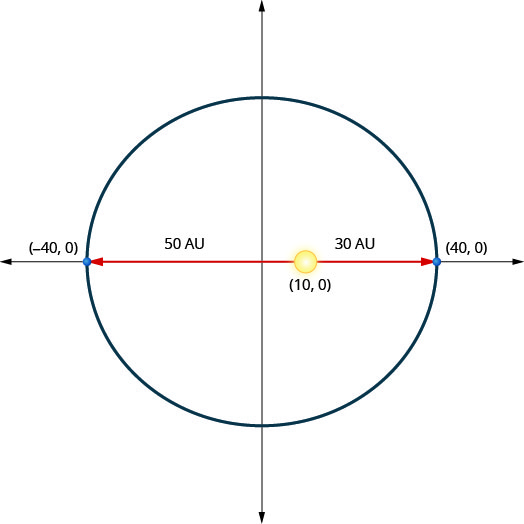
    Ce graphique montre une ellipse avec un centre (0, 0) et des sommets (moins 40, 0) et (40, 0). Le soleil est représenté au point (10, 0). Cela se trouve à 30 unités du sommet droit et à 50 unités du sommet gauche.
    Graphique 11.3.34

    Solution :

    Nous reconnaissons qu'il s'agit d'une ellipse centrée à l'origine.

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

    Puisque l'axe principal est horizontal et que la distance entre le centre et le sommet l'est\(40\), nous le savons\(a=40\) et ainsi de suite\(a^{2}=1600\).

    \(\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1\)

    L'axe secondaire est vertical mais les points d'extrémité ne sont pas indiqués. Pour le trouver,\(b\) nous utiliserons la position du Soleil. Puisque le Soleil est au centre de l'ellipse au point\((10,0)\), nous le savons\(c=10\). Utilisez ceci pour résoudre\(b^{2}\).

    \(b^{2}=a^{2}-c^{2}\)
    \(b^{2}=40^{2}-10^{2}\)
    \(b^{2}=1600-100\)
    \(b^{2}=1500\)

    Remplacez\(a^{2}\) et\(b^{2}\) dans la forme standard de l'ellipse.

    \(\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1\)

    Exercice\(\PageIndex{13}\)

    Une planète se déplace sur une orbite elliptique autour de son soleil. Le plus proche que la planète se rapproche du soleil se trouve approximativement\(20\) au et le plus éloigné se trouve à peu près\(30\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la planète.

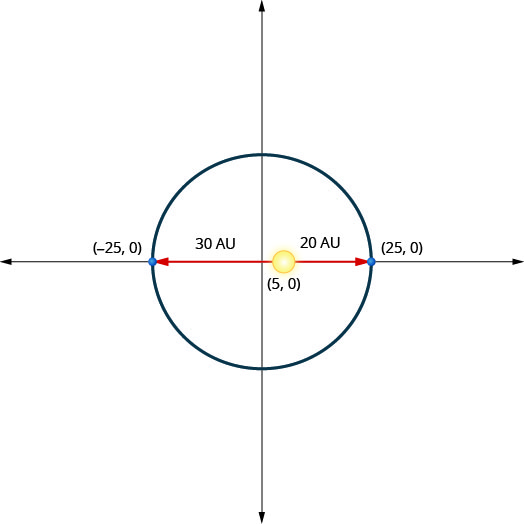
    Ce graphique montre une ellipse avec un centre (0, 0) et des sommets (moins 25, 0) et (25, 0). Le soleil est représenté au point (5, 0). C'est à 20 unités du sommet droit et à 30 unités du sommet gauche.
    Graphique 11.3.35
    Réponse

    \(\frac{x^{2}}{625}+\frac{y^{2}}{600}=1\)

    Exercice\(\PageIndex{14}\)

    Une planète se déplace sur une orbite elliptique autour de son soleil. Le plus proche que la planète se rapproche du soleil se trouve approximativement\(20\) au et le plus éloigné se trouve à peu près\(50\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la planète.

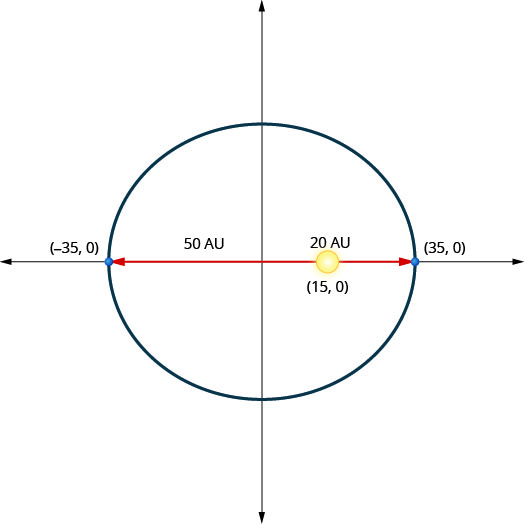
    Ce graphique montre une ellipse avec un centre (0, 0) et des sommets (moins 35, 0) et (35, 0). Le soleil est représenté au point (15, 0). C'est à 20 unités du sommet droit et à 50 unités du sommet gauche.
    Graphique 11.3.36
    Réponse

    \(\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1\)

    Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les ellipses.

    • Sections coniques : représentation graphique d'ellipses, partie 1
    • Sections coniques : représentation graphique d'ellipses, partie 2
    • Équation de l'ellipse à partir d'

    Concepts clés

    • Ellipse : Une ellipse est constituée de tous les points d'un plan où la somme des distances entre deux points fixes est constante. Chacun des points fixes est appelé foyer de l'ellipse.
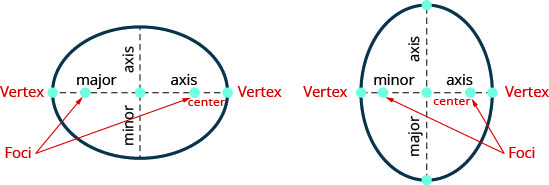
      Cette figure montre deux ellipses. Dans chacun d'eux, deux points de l'ellipse sont appelés foyers. Une ligne tracée à travers les foyers coupe l'ellipse en deux points. Chaque point est étiqueté sommet. Dans la figure de gauche, le segment reliant les sommets est appelé axe principal. Un segment perpendiculaire à l'axe principal qui passe par son point médian et coupe l'ellipse en deux points est appelé axe secondaire. L'axe principal est plus long que l'axe secondaire. Dans la figure de droite, le segment passant par les foyers, reliant les sommets est plus court et est étiqueté axe mineur. Son point médian est étiqueté centre.

    Graphique 11.3.37

    • Si nous tracons une ligne à travers les foyers, l'ellipse croise en deux points, chacun étant appelé sommet de l'ellipse.
      Le segment reliant les sommets est appelé axe principal.
      Le milieu du segment est appelé le centre de l'ellipse.
      Un segment perpendiculaire à l'axe principal qui passe par le centre et coupe l'ellipse en deux points est appelé axe secondaire.
    • Forme standard de l'équation, une ellipse avec un centre\((0,0)\) : La forme standard de l'équation d'une ellipse avec un centre\((0,0)\) est

      \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)

      Les\(x\) -intercepts sont\((a,0)\) et\((−a,0)\).
      Les\(y\) -intercepts sont\((0,b)\) et\((0,−b)\).
    • Comment créer une ellipse avec centre\((0,0)\)
      1. Écrivez l'équation sous forme standard.
      2. Déterminez si l'axe principal est horizontal ou vertical.
      3. Trouvez les extrémités de l'axe principal.
      4. Trouvez les extrémités de l'axe secondaire
      5. Esquissez l'ellipse.
    • Forme standard de l'équation, une ellipse avec un centre\((h,k)\) : La forme standard de l'équation d'une ellipse avec un centre\((h,k)\) est

      \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)

      Lorsque\(a>b\), l'axe principal est horizontal, de sorte que la distance entre le centre et le sommet est de\(a\).
      Lorsque\(b>a\), l'axe principal est vertical, de sorte que la distance entre le centre et le sommet est de\(b\).

    Lexique

    ellipse
    Une ellipse est constituée de tous les points d'un plan où la somme des distances entre deux points fixes est constante.