Skip to main content
Global

11.4E : Exercices

  1. Last updated
  2. Save as PDF
  • Page ID
    194544

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    La pratique rend la perfection

    Exercice\(\PageIndex{15}\) Graph an Ellipse with Center at the Origin

    Dans les exercices suivants, tracez chaque ellipse.

    1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    3. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    4. \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
    5. \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
    6. \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
    7. \(x^{2}+\frac{y^{2}}{4}=1\)
    8. \(\frac{x^{2}}{9}+y^{2}=1\)
    9. \(4 x^{2}+25 y^{2}=100\)
    10. \(16 x^{2}+9 y^{2}=144\)
    11. \(16 x^{2}+36 y^{2}=576\)
    12. \(9 x^{2}+25 y^{2}=225\)
    Réponse

    1.

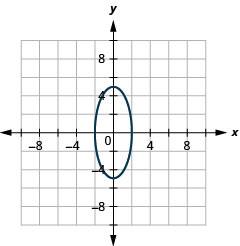
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 5) et (0, moins 5) et des extrémités de l'axe secondaire (2, 0) et (négatif 2, 0).
    Graphique 11.3.38

    3.

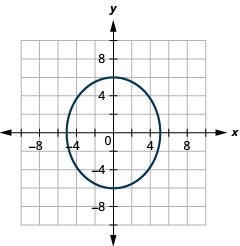
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 6) et (0, moins 6) et des extrémités de l'axe secondaire (5, 0) et (négatif 5, 0).
    Graphique 11.3.39

    5.

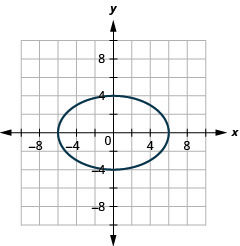
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (6, 0) et (moins 6, 0) et des extrémités de l'axe secondaire (0, 4) et (0, négatif 4).
    Graphique 11.3.40

    7.

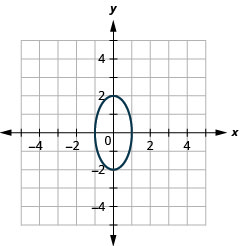
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 2) et (0, moins 2) et des extrémités de l'axe secondaire (1, 0) et (négatif 1, 0).
    Graphique 11.3.41

    9.

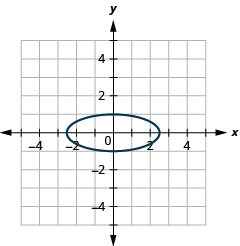
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (5, 0) et (moins 5, 0) et des extrémités de l'axe secondaire (0, 2) et (0, moins 2).
    Graphique 11.3.42

    11.

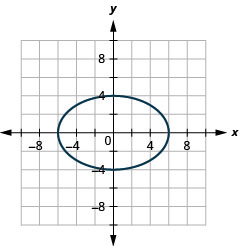
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (6, 0) et (moins 6, 0) et des extrémités de l'axe secondaire (0, 4) et (0, négatif 4).
    Graphique 11.3.43
    Exercice\(\PageIndex{16}\) Find the Equation of an Ellipse with Center at the Origin

    Dans les exercices suivants, trouvez l'équation de l'ellipse illustrée sur le graphique.

    1.

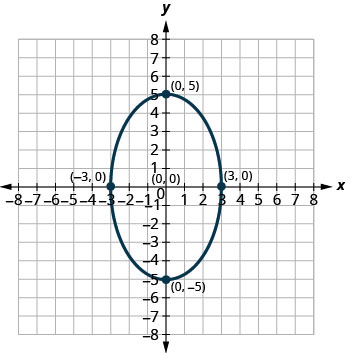
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 5) et (0, moins 5) et des extrémités de l'axe secondaire (négatif 3, 0) et (3, 0).
    Graphique 11.3.4

    2.

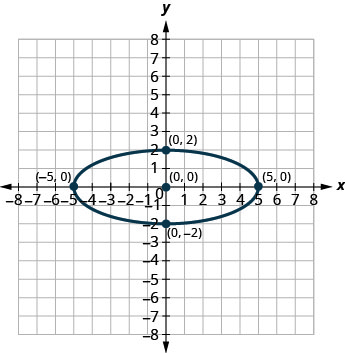
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (5, 0) et (moins 5, 0) et des extrémités de l'axe secondaire (0, 2) et (0, moins 2).
    Graphique 11.3.45

    3.

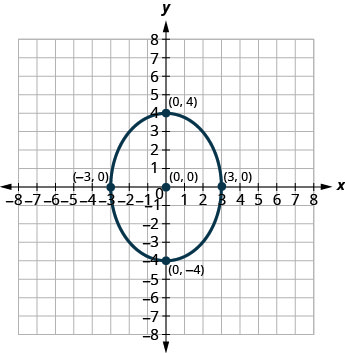
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 4) et (0, moins 4) et des extrémités de l'axe secondaire (négatif 3, 0) et (3, 0).
    Graphique 11.3.46

    4.

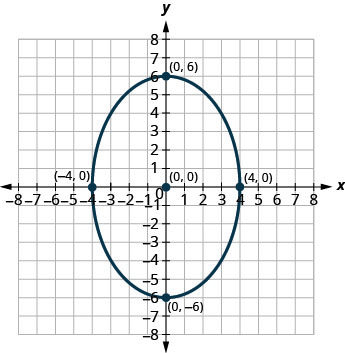
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 6) et (0, moins 6) et des extrémités de l'axe secondaire (négatif 4, 0) et (4, 0).
    Graphique 11.3.47
    Réponse

    1. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)

    3. \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)

    Exercice\(\PageIndex{17}\) Graph an Ellipse with Center Not at the Origin

    Dans les exercices suivants, tracez chaque ellipse.

    1. \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
    2. \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
    3. \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
    4. \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
    Réponse

    1.

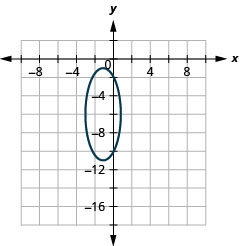
    Ce graphique montre une ellipse avec un centre (négatif 1, moins 6), des sommets (négatif 1, moins 1) et (négatif 1, négatif 11) et des extrémités de l'axe mineur (négatif 3, moins 6) et (1, négatif 6).
    Graphique 11.3.48

    3.

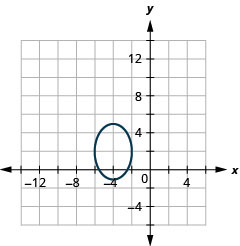
    Ce graphique montre une ellipse avec un centre (négatif 4, 2), des sommets (négatif 4, 5) et (négatif 4, moins 1) et des extrémités du petit axe (3, 1) et (négatif 6, 2) et (négatif 2, 2) et (négatif 2, 2).
    Graphique 11.3.49
    Exercice\(\PageIndex{18}\) Graph an Ellipse with Center Not at the Origin

    Dans les exercices suivants, tracez chaque équation par translation.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
    2. \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
    3. \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
    4. \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
    Réponse

    1.

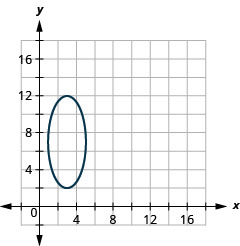
    Ce graphique montre une ellipse avec un centre (3, 7), des sommets (3, 2) et (3, 12) et les extrémités des axes secondaires (1, 7) et (5, 7).
    Graphique 11.3.50

    3.

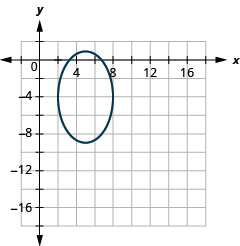
    Ce graphique montre une ellipse avec un centre (5, moins 4), des sommets (5, 1) et (5, moins 9) et des extrémités du petit axe (2, moins 4) et (8, moins 4).
    Graphique 11.3.51
    Exercice\(\PageIndex{19}\) Graph an Ellipse with Center Not at the Origin

    Dans les exercices suivants,

    1. Écrivez l'équation sous forme standard et
    2. Graphe.
    1. \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
    2. \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
    3. \(4 x^{2}+25 y^{2}-24 x-64=0\)
    4. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    Réponse

    1.

    1. \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
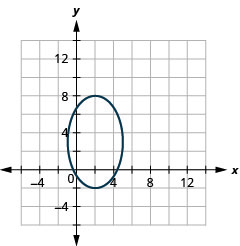
    Ce graphique montre une ellipse avec un centre (2, 3), des sommets (2, moins 2) et (2, 8) et des extrémités d'un axe mineur (moins 1, 3) et (5, 3).
    Graphique 11.3.52

    3.

    1. \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
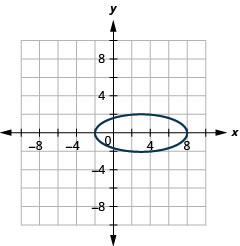
    Ce graphique montre une ellipse avec un centre (3, 0), des sommets (moins 2, 0) et (8, 0) et les extrémités du petit axe (3, 2) et (3, négatif 2).
    Graphique 11.3.53
    Exercice\(\PageIndex{20}\) Graph an Ellipse with Center Not at the Origin

    Dans les exercices suivants, tracez l'équation.

    1. \(x=-2(y-1)^{2}+2\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \(y=-x^{2}+8 x-15\)
    5. \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
    6. \((x-2)^{2}+(y-3)^{2}=9\)
    7. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    8. \(x=4(y+1)^{2}-4\)
    9. \(x^{2}+y^{2}=64\)
    10. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    11. \(y=6 x^{2}+2 x-1\)
    12. \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
    Réponse

    1.

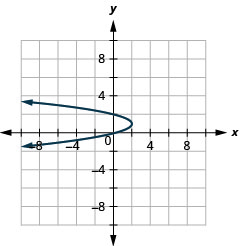
    Ce graphique montre une parabole avec un sommet (2, 1) et des intersections y (0, 0) et (2, 0).
    Graphique 11.3.54

    3.

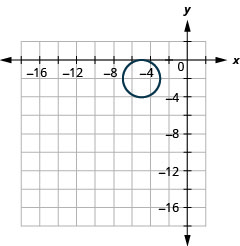
    Ce graphique montre un cercle avec un centre (moins 5, moins 2) et un rayon de 2 unités.
    Graphique 11.3.5

    5.

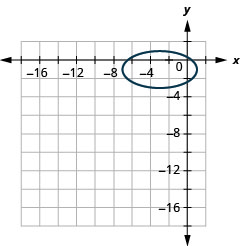
    Ce graphique montre une ellipse avec un centre (négatif 3, moins 1), des sommets (1, négatif 1) et (négatif 7, négatif 1) et des extrémités de l'axe mineur (négatif 3, 1) et (négatif 3, négatif 3).
    Graphique 11.3.56

    7.

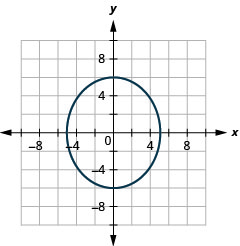
    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (0, 6) et (0, moins 6) et des extrémités de l'axe secondaire (négatif 5, 0) et (5, 0).
    Graphique 11.3.57

    9.

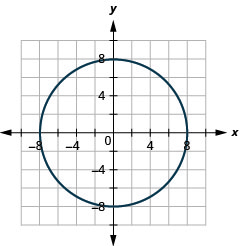
    Ce graphique montre un cercle avec un centre (0, 0) et un rayon de 8 unités.
    Graphique 11.3.58

    11.

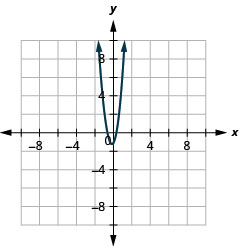
    Ce graphique montre une parabole s'ouvrant vers le haut. Son sommet a une valeur x légèrement inférieure à 0 et une valeur y légèrement inférieure à moins 1. Un point y est approximativement égal à (négatif 1, 3).
    Graphique 11.3.59
    Exercice\(\PageIndex{21}\) Solve Application with Ellipses

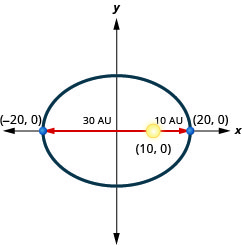
    1. Une planète se déplace sur une orbite elliptique autour de son soleil. Le plus proche que la planète se rapproche du soleil se trouve approximativement\(10\) au et le plus éloigné se trouve à peu près\(30\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la planète.

    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (moins 20, 0) et (20, 0). Le soleil est représenté au point (10, 0), qui se trouve à 30 unités du sommet gauche et à 10 unités du sommet droit.
    Graphique 11.3.60

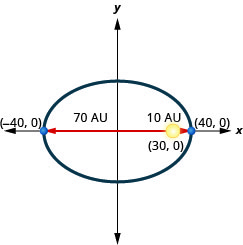
    2. Une planète se déplace sur une orbite elliptique autour de son soleil. Le plus proche que la planète se rapproche du soleil se trouve approximativement\(10\) au et le plus éloigné se trouve à peu près\(70\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la planète.

    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (moins 40, 0) et (40, 0). Le soleil est représenté au point (30, 0), qui se trouve à 70 unités du sommet gauche et à 10 unités du sommet droit.
    Graphique 11.3.61

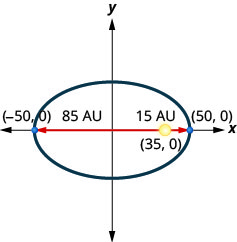
    3. Une comète se déplace sur une orbite elliptique autour du soleil. La comète se rapproche le plus du soleil approximativement\(15\) au et la plus éloignée se trouve à peu près\(85\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la comète.

    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (moins 50, 0) et (50, 0). Le soleil est représenté au point (35, 0), qui se trouve à 85 unités du sommet gauche et à 15 unités du sommet droit.
    Graphique 11.3.62

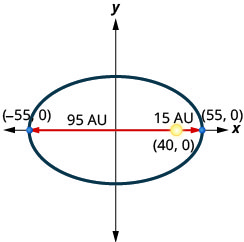
    4. Une comète se déplace sur une orbite elliptique autour du soleil. La comète se rapproche le plus du soleil approximativement\(15\) au et la plus éloignée se trouve à peu près\(95\) au UA. Le soleil est l'un des foyers de l'orbite elliptique. En laissant l'ellipse se centrer sur l'origine et en étiquetant les axes en UA, l'orbite ressemblera à la figure ci-dessous. Utilisez le graphique pour écrire une équation pour l'orbite elliptique de la comète.

    Ce graphique montre une ellipse avec un centre (0, 0), des sommets (moins 55, 0) et (55, 0). Le soleil est représenté au point (40, 0), qui se trouve à 95 unités du sommet gauche et à 15 unités du sommet droit.
    Graphique 11.3.63
    Réponse

    1. \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)

    3. \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)

    Exercice\(\PageIndex{22}\) Writing Exercises
    1. En vos propres termes, définissez une ellipse et écrivez l'équation d'une ellipse centrée sur l'origine sous une forme standard. Dessinez une esquisse de l'ellipse en indiquant le centre, les sommets et les axes principaux et secondaires.
    2. Expliquez avec vos propres mots comment obtenir les axes de l'équation sous forme standard.
    3. Comparez et contrastez les graphes des équations\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) et\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).
    4. Expliquez avec vos propres mots la différence entre un sommet et le centre de l'ellipse.
    Réponse

    1. Les réponses peuvent varier

    3. Les réponses peuvent varier

    Auto-vérification

    a. Une fois les exercices terminés, utilisez cette liste de contrôle pour évaluer votre maîtrise des objectifs de cette section.

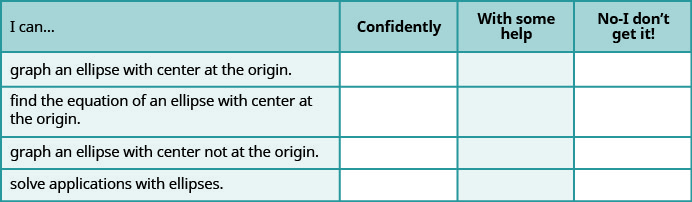
    Ce tableau comporte 4 colonnes, 4 lignes et une ligne d'en-tête. La ligne d'en-tête étiquette chaque colonne que je peux, en toute confiance, avec de l'aide et non, je ne comprends pas.™ Les premières colonnes contiennent les instructions suivantes : tracez une ellipse dont le centre est à l'origine, trouvez l'équation d'une ellipse dont le centre est à l'origine, tracez une ellipse dont le centre n'est pas à l'origine, résolvez des applications avec des ellipses. Les colonnes restantes sont vides.
    Graphique 11.3.64

    b. Qu'est-ce que cette liste de contrôle vous apprend sur votre maîtrise de cette section ? Quelles mesures allez-vous prendre pour vous améliorer ?