Skip to main content
Global

11.5 : Hyperboles

  1. Last updated
  2. Save as PDF
  • Page ID
    194510

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Tracez une hyperbole avec le centre à\((0,0)\)
    • Tracez une hyperbole avec le centre à\((h,k)\)
    • Identifier les sections coniques par leurs équations

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Résoudre :\(x^{2}=12\).
      Si vous avez oublié ce problème, consultez l'exemple 9.1.
    2. Agrandir :\((x−4)^{2}\).
      Si vous avez oublié ce problème, consultez l'exemple 5.32.
    3. Graphe\(y=-\frac{2}{3} x\).
      Si vous avez oublié ce problème, consultez l'exemple 3.4.

    Tracez une hyperbole avec le centre à\((0,0)\)

    La dernière section conique que nous allons examiner s'appelle une hyperbole. Nous verrons que l'équation d'une hyperbole ressemble à l'équation d'une ellipse, sauf qu'il s'agit d'une différence plutôt que d'une somme. Bien que les équations d'une ellipse et d'une hyperbole soient très similaires, leurs graphes sont très différents.

    Nous définissons une hyperbole comme tous les points d'un plan où la différence de leurs distances par rapport à deux points fixes est constante. Chacun des points fixes est appelé foyer de l'hyperbole.

    Définition\(\PageIndex{1}\)

    Une hyperbole est l'ensemble des points d'un plan où la différence de leurs distances par rapport à deux points fixes est constante. Chacun des points fixes est appelé foyer de l'hyperbole.

    La figure montre un cône circulaire droit à double emboîtement tranché par un plan parallèle à l'axe vertical du cône formant une hyperbole. La figurine est étiquetée « hyperbole »™.
    Graphique 11.4.1

    La ligne passant par les foyers s'appelle l'axe transversal. Les deux points où l'axe transversal croise l'hyperbole sont chacun un sommet de l'hyperbole. Le milieu du segment joignant les foyers est appelé le centre de l'hyperbole. La ligne perpendiculaire à l'axe transversal qui passe par le centre est appelée axe conjugué. Chaque élément du graphique est appelé une branche de l'hyperbole.

    La figure montre deux graphiques d'une hyperbole. Le premier graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets et les foyers sont représentés par des points situés sur l'axe transversal, qui est l'axe X. Les branches passent par les sommets et s'ouvrent à gauche et à droite. L'axe Y est l'axe conjugué. Le deuxième graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets et les foyers sont représentés par des points situés sur l'axe transversal, qui est l'axe y. Les branches passent par les sommets et s'ouvrent de haut en bas. L'axe X est l'axe conjugué.
    Graphique 11.4.2

    Encore une fois, notre objectif est de relier la géométrie d'une conique à l'algèbre. Le fait de placer l'hyperbole sur un système de coordonnées rectangulaires nous donne cette opportunité. Dans la figure, nous avons placé l'hyperbole de manière à ce que\(((−c,0),(c,0))\) les foyers soient sur l'\(x\)axe -et que le centre soit l'origine.

    La figure montre le graphique d'une hyperbole. Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les foyers (c, 0 négatifs) et (c, 0) sont marqués d'un point et se situent sur l'axe des abscisses. Les sommets sont marqués d'un point et se situent sur l'axe des abscisses. Les branches passent par les sommets et s'ouvrent à gauche et à droite. La distance entre (négatif c, 0) et un point de la branche (x, y) est marquée d sub 1. La distance entre (x, y) sur la branche et (c, 0) est marquée d sub 2.
    Graphique 11.4.3

    La définition indique que la différence de distance entre les foyers et un point\((x,y)\) est constante. Il en\(|d_{1}−d_{2}|\) est de même pour nous une constante que nous appellerons\(2a\) ainsi\(|d_{1}-d_{2} |=2 a\). Nous utiliserons la formule de distance pour nous amener à une formule algébrique pour une ellipse.

    \(\left|d_{1} - d_{2}\right| =2 a\)

    Utilisez la formule de distance pour trouver\(d_{1}, d_{2}\)

    \(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)

    Éliminez les radicaux. Pour simplifier l'équation de l'ellipse, nous laissons\(c^{2}-a^{2}=b^{2}\).

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)

    Ainsi, l'équation d'une hyperbole centrée à l'origine sous forme standard est la suivante :

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)

    Pour représenter graphiquement l'hyperbole, il sera utile de connaître les interceptions. Nous trouverons les\(x\) -intercepts et\(y\) -intercepts en utilisant la formule.

    \(x\)-intercepte

    Laissez\(y=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)

    Les\(x\) -intercepts sont\((a,0)\) et\((−a,0)\).

    \(y\)-intercepte

    Laissez\(x=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)

    Il n'y a pas\(y\) de -intercepts.

    Les\(a, b\) valeurs de l'équation nous aident également à trouver les asymptotes de l'hyperbole. Les asymptotes sont des lignes droites croisées que les branches du graphe approchent mais ne se croisent jamais lorsque les\(x, y\) valeurs s'agrandissent.

    Pour trouver les asymptotes, nous esquissons un rectangle dont les côtés croisent l'axe x aux sommets\((−a,0),(a,0)\) et l'\(y\)axe -à\((0,−b), (0,b)\). Les lignes contenant les diagonales de ce rectangle sont les asymptotes de l'hyperbole. Le rectangle et les asymptotes ne font pas partie de l'hyperbole, mais ils nous aident à représenter graphiquement l'hyperbole.

    La figure montre le graphique d'une hyperbole. Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets sont (négatif a, 0) et (a, 0), sont marqués d'un point et se situent sur l'axe des abscisses. Les points (0, b) et (0, négatif) se situent sur l'axe Y. Il existe un rectangle central dont les côtés coupent l'axe X aux sommets (négatif a, 0) et (a, 0) et coupent l'axe y en (0, b) et (0, négatif b). Les asymptotes sont données par y est égal à b divisé par a fois x et y est égal à moins b divisé par a fois x et sont dessinées comme les diagonales du rectangle central. Les branches de l'hyperbole passent par les sommets, s'ouvrent à gauche et à droite et s'approchent des asymptotes.
    Graphique 11.4.4

    Les asymptotes passent par l'origine et nous pouvons évaluer leur pente à l'aide du rectangle que nous avons esquissé. Ils ont des équations\(y=\frac{b}{a} x\) et\(y=-\frac{b}{a} x\).

    Il existe deux équations pour les hyperboles, selon que l'axe transversal est vertical ou horizontal. Nous pouvons déterminer si l'axe transversal est horizontal en regardant l'équation. Lorsque l'équation est sous forme standard, si le\(x^{2}\) terme -est positif, l'axe transversal est horizontal. Lorsque l'équation est sous forme standard, si le\(y^{2}\) terme est positif, l'axe transversal est vertical.

    Les deuxièmes équations pourraient être dérivées de la même manière que nous avons fait. Nous allons résumer les résultats ici.

    Définition\(\PageIndex{2}\)

    Forme standard de l'équation : une hyperbole avec un centre\((0,0)\)

    La forme standard de l'équation d'une hyperbole avec centre\((0,0)\) est

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\)ou\(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)

    La figure montre le graphique de deux hyperboles. Le premier graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets sont (négatif a, 0) et (a, 0), sont marqués d'un point et se situent sur l'axe des abscisses. Les points (0, b) et (0, négatif) se situent sur l'axe Y. Il existe un rectangle central dont les côtés coupent l'axe X aux sommets (négatif a, 0) et (a, 0) et coupent l'axe y en (0, b) et (0, négatif b). Les asymptotes sont données par y est égal à b divisé par a fois x et y est égal à moins b divisé par a fois x et sont dessinées comme les diagonales du rectangle central. Les branches de l'hyperbole passent par les sommets, s'ouvrent à gauche et à droite et s'approchent des asymptotes. Le deuxième graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets sont (0, a) et (0, négatif a), sont marqués d'un point et se situent sur l'axe y. Les points (0, b) et (0, négatif) se situent sur l'axe Y. Il existe un rectangle central dont les côtés coupent l'axe y aux sommets (0, a) et (0, négatif a) et coupent l'axe y en (négatif b, 0) et (b, 0). Les branches de l'hyperbole traversent les sommets, s'ouvrent de haut en bas et s'approchent des asymptotes.
    Graphique 11.4.5

    Notez que, contrairement à l'équation d'une ellipse, le dénominateur de n'\(x^{2}\)est pas toujours\(a^{2}\) et le dénominateur de n'\(y^{2}\)est pas toujours\(b^{2}\).

    Notez que lorsque le\(x^{2}\) terme est positif, l'axe transversal se trouve sur l'\(x\)axe. Lorsque le\(y^{2}\) terme « -term » est positif, l'axe transversal se trouve sur l'\(y\)axe « ».

    Formes standard de l'équation : une hyperbole avec un centre\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    Orientation \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >Axe transversal sur l'\(x\)axe.
    S'ouvre à gauche et à droite    		 \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >Axe transversal sur l'\(y\)axe.
    S'ouvre de haut en bas
    Sommets \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >\((0,-a),(0, a)\)
    \(x\)-intercepte \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >aucun
    \(y\)-intercepte \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >aucun \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >\((0,-a),(0, a)\)
    Rectangle \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >Utiliser\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >Utiliser\((0, \pm a)( \pm b, 0)\)
    Asymptomtotes \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    Tableau 11.4.1

    Nous utiliserons ces propriétés pour représenter graphiquement les hyperboles.

    Exemple\(\PageIndex{1}\) How to Graph a Hyperbola with Center \((0,0)\)

    Graphe\(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\).

    Solution :

    Étape 1 : Écrivez l'équation sous forme standard. L'équation se présente sous forme standard. \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\)
    Étape 2 : Déterminez si l'axe transversal est horizontal ou vertical. Le\(x^{2}\) terme -étant positif, l'axe transversal est horizontal. L'axe transversal est horizontal.
    Étape 3 : Trouvez les sommets Depuis\(a^{2}=25\) lors\(a=\pm 5\). Les sommets se situent sur l'\(x\)axe. \((-5,0),(5,0)\)
    Étape 4 : Esquissez le rectangle centré à l'intersection d'origine d'un axe\(\pm a\) et de l'autre\(\pm b\).

    Puisque\(a=\pm 5\), le rectangle va croiser l'\(x\)axe -au niveau des sommets.

    Puisque\(b=\pm 2\), le rectangle va croiser l'\(y\)axe -en\((0,-2)\) et\((0,2)\).

    		 Capture d'écran (148) .png

    Étape 5 : Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle.

    		 Les asymptotes ont les équations\(y=\frac{5}{2} x, y=-\frac{5}{2} x\). Capture d'écran (149) .png
    Étape 6 : Dessinez les deux branches de l'hyperbole. Commencez par chaque sommet et utilisez les asymptotes comme guide. 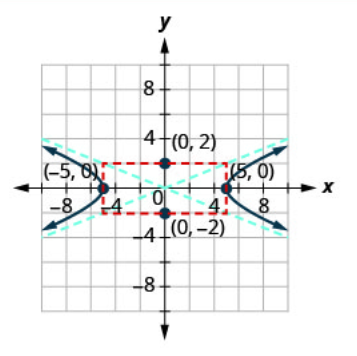Capture d'écran (150) .png
    Tableau 11.4.2
    Exercice\(\PageIndex{1}\)

    Graphe\(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\).

    Réponse
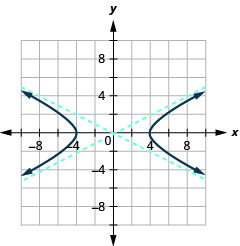
    Le graphique montre les axes x et y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec des asymptotes y étant égales à plus ou moins une demie fois x, et des branches qui passent par les sommets (plus ou moins 4, 0) et s'ouvrent à gauche et à droite.
    Graphique 11.4.9
    Exercice\(\PageIndex{2}\)

    Graphe\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\).

    Réponse
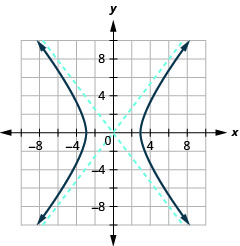
    Le graphique montre les axes x et y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec des asymptotes y étant égales à plus ou moins quatre tiers fois x, et des branches qui passent par les sommets (plus ou moins 3, 0) et s'ouvrent à gauche et à droite.
    Graphique 11.4.10

    Nous résumons les étapes à titre de référence.

    Tracez une hyperbole centrée sur\((0,0)\)

    1. Écrivez l'équation sous forme standard.
    2. Déterminez si l'axe transversal est horizontal ou vertical.
    3. Trouvez les sommets.
    4. Esquissez le rectangle centré à l'origine en coupant un axe à\(±a\) et l'autre à\(±b\).
    5. Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle.
    6. Dessine les deux branches de l'hyperbole.

    Parfois, l'équation d'une hyperbole doit d'abord être placée sous forme standard avant de la représenter graphiquement.

    Exemple\(\PageIndex{2}\)

    Graphe\(4 y^{2}-16 x^{2}=64\).

    Solution :

      \(4 y^{2}-16 x^{2}=64\)
    Pour écrire l'équation sous forme standard, divisez chaque terme par\(64\) pour que l'équation soit égale à\(1\). \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\)
    Simplifiez. \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\)
    Le\(y^{2}\) terme -étant positif, l'axe transversal est vertical. Depuis\(a^{2}=16\) lors\(a=\pm 4\).  
    Les sommets se situent sur l'\(y\)axe -,\((0,-a),(0, a)\). Depuis\(b^{2}=4\) lors\(b=\pm 2\). \((0,-4),(0,4)\)
    Esquissez le rectangle croisant l'\(x\)axe\((-2,0),(2,0)\) -et l'\(y\)axe -au niveau des sommets. Esquissez les asymptotes à travers les diagonales du rectangle. Dessine les deux branches de l'hyperbole. .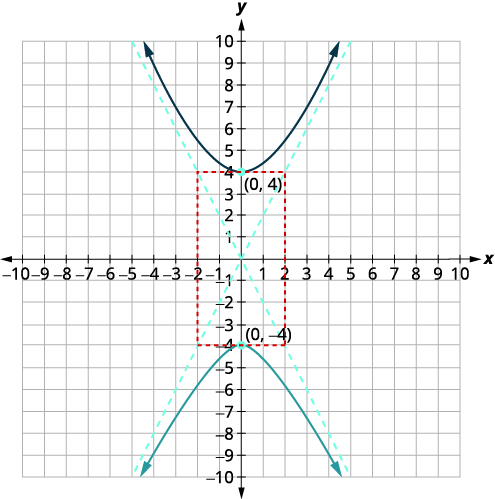
    Tableau 11.4.3
    Exercice\(\PageIndex{3}\)

    Graphe\(4 y^{2}-25 x^{2}=100\).

    Réponse
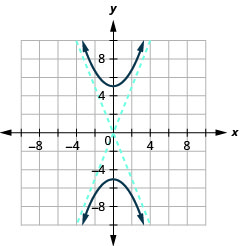
    Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec des asymptotes y étant égales à plus ou moins cinq moitiés fois x, et des branches qui passent par les sommets (0, plus ou moins 5) et s'ouvrent de haut en bas.
    Graphique 11.4.12
    Exercice\(\PageIndex{4}\)

    Graphe\(25 y^{2}-9 x^{2}=225\).

    Réponse
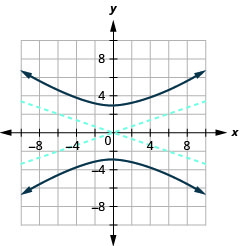
    Le graphique montre les axes x et y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec des asymptotes y étant égales à plus ou moins trois cinquièmes fois x, et des branches qui passent par les sommets (0, plus ou moins 3) et s'ouvrent de haut en bas.
    Graphique 11.4.13

    Tracez une hyperbole avec le centre à\((h,k)\)

    Les hyperboles ne sont pas toujours centrées à l'origine. Lorsqu'une hyperbole est centrée sur\((h,k)\) les équations, cela change légèrement, comme indiqué dans le tableau.

    Formes standard de l'équation : une hyperbole avec un centre\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    Orientation \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >L'axe transversal est horizontal. S'ouvre à gauche et à droite \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >L'axe transversal est vertical. S'ouvre de haut en bas
    Centre \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >\((h,k)\) \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >\((h,k)\)
    Sommets \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >\(a\) unités à gauche et à droite du centre \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >\(a\) unités au-dessus et en dessous du centre
    Rectangle \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >Utiliser les\(a\) unités gauche/droite des\(b\) unités centrales au-dessus ou en dessous du centre \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >Utiliser les\(a\) unités au-dessus ou en dessous des\(b\) unités centrales gauche/droite du centre
    Tableau 11.4.4
    Exemple\(\PageIndex{3}\) How to Graph a Hyperbola with Center \((h,k)\)

    Graphe\(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)

    Solution :

    Étape 1 : Écrivez l'équation sous forme standard. L'équation se présente sous forme standard. \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
    Étape 2 : Déterminez si l'axe transversal est horizontal ou vertical. Le\(x^{2}\) terme -étant positif, l'hyperbole s'ouvre à gauche et à droite. L'axe transversal est horizontal. L'hyperbole s'ouvre à gauche et à droite.
    Étape 3 : Trouvez le centre et\(a, b\). \(h=1\)et\(k=2\)
    \(a^{2}=9\)
    \(b^{2}=16\)

    \(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\)

    Centre :\((1,2)\)

    \(a=3\)

    \(b=4\)
    Étape 4 : Esquissez le rectangle centré lors de\((h,k)\) l'utilisation\(a,b\).

    Marquez le centre,\((1,2)\).

    Esquissez le rectangle qui passe par les\(3\) unités de points situées à gauche/droite du centre et les\(4\) unités situées au-dessus et en dessous du centre.

    		 Capture d'écran (151) .png
    Étape 5 : Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle. Marquez les sommets. Esquissez les diagonales. Marquez les sommets, qui se trouvent sur les\(3\) unités du rectangle à gauche et à droite du centre. Capture d'écran (152) .png
    Étape 6 : Dessinez les deux branches de l'hyperbole. Commencez par chaque sommet et utilisez les asymptotes comme guide. Capture d'écran (153) .png
    Tableau 11.4.5
    Exercice\(\PageIndex{5}\)

    Graphe\(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\).

    Réponse
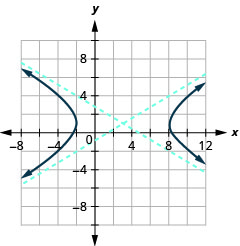
    Le graphique montre les axes x et y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec une asymptote qui passe par (négatif 2, négatif 2) et (8, 4) et une asymptote qui passe par (négatif 2, 4) et (8, négatif 2), et des branches qui passent par les sommets ( négatif 2, 2) et (8, 2) et s'ouvre à gauche et à droite.
    Figure 11.4.17
    Exercice\(\PageIndex{6}\)

    Graphe\(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\).

    Réponse
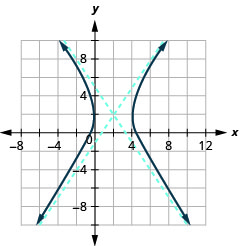
    Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec le centre (2, 2), une asymptote qui passe par (0, négatif 1) et (4, 5) et une asymptote qui passe par (0, 5) et (4, négatif 1), et des branches qui passent par les sommets (0, 2) et (4, 2) et s'ouvre à gauche et à droite.
    Graphique 11.4.18

    Nous résumons les étapes pour faciliter la consultation.

    Tracez une hyperbole centrée sur\((h,k)\)

    1. Écrivez l'équation sous forme standard.
    2. Déterminez si l'axe transversal est horizontal ou vertical.
    3. Trouvez le centre et\(a,b\).
    4. Esquissez le rectangle centré lors de\((h,k)\) l'utilisation\(a,b\).
    5. Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle. Marquez les sommets.
    6. Dessine les deux branches de l'hyperbole.

    Soyez prudent lorsque vous identifiez le centre. L'équation standard a\(x−h\) et\(y−k\) avec le centre comme\((h,k)\).

    Exemple\(\PageIndex{4}\)

    Graphe\(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\).

    Solution :

      .
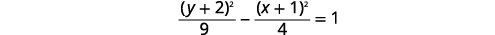    Le\(y^{2}\) terme -étant positif, l'hyperbole s'ouvre de haut en bas. .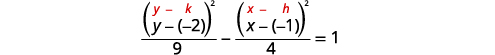
    Trouvez le centre,\((h,k)\). Centre :\((-1,-2)\)
    Trouve\(a,b\). \(a=3 b=2\)
    Esquissez le rectangle qui passe par les\(3\) unités de points au-dessus et en dessous du centre et les
    \(2\) unités situées à gauche/droite du centre.
    Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle.
    Marquez les sommets.
    Tracez les branches.    		 .
    Tableau 11.4.6
    Exercice\(\PageIndex{7}\)

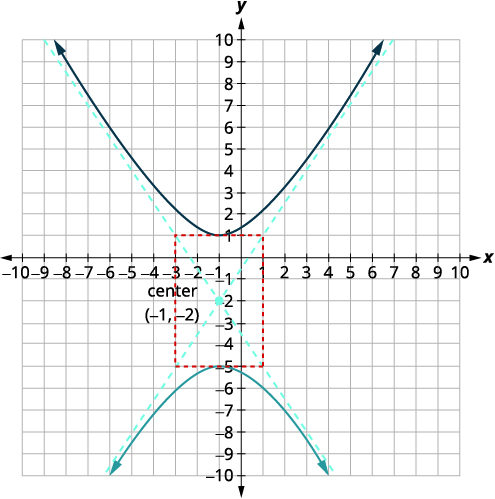    Graphe\(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\).

    Réponse
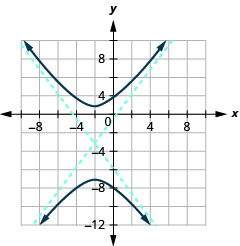
    Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec un centre à (négatif 2, négatif 3), une asymptote qui passe à travers (négatif 5, négatif 7) et (1, 1) et une asymptote qui passe à travers (négatif 5, 1) et (1, 7), et des branches qui passent par les sommets (moins 2, 1) et (moins 2, moins 7) et s'ouvrent de haut en bas.
    Graphique 11.4.22
    Exercice\(\PageIndex{8}\)

    Graphe\(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\).

    Réponse
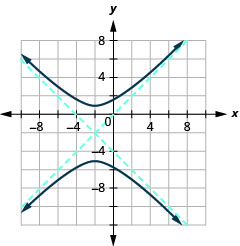
    Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec un centre à (négatif 2, négatif 2), une asymptote qui passe par (négatif 5, négatif 5) et (1, 1) et une asymptote qui passe par (négatif 5, 1) et (1, négatif 5), et branches qui passent par les sommets (négatif 2, 1) et (négatif 2, négatif 5) et s'ouvrent de haut en bas.
    Graphique 11.4.23

    Encore une fois, nous devons parfois mettre l'équation sous forme standard dans un premier temps.

    Exemple\(\PageIndex{5}\)

    Écrivez l'équation sous une forme et un graphique standard\(4 x^{2}-9 y^{2}-24 x-36 y-36=0\).

    Solution :

      .
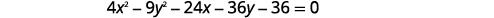    Pour accéder au formulaire standard, complétez les cases. .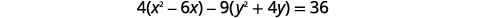
      .
      .
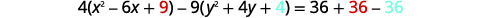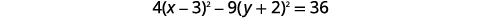    Divisez chaque terme par\(36\) pour obtenir la constante\(1\). .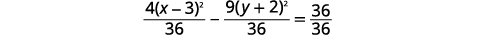
      .
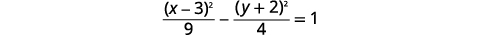    Le\(x^{2}\) terme -étant positif, l'hyperbole s'ouvre à gauche et à droite.  
    Trouvez le centre,\((h,k)\). Centre :\((3, -2)\)
    Trouve\(a,b\).

    \(a=3\)

    \(b=4\)
    Esquissez le rectangle qui passe par les\(3\) unités de points situées à gauche/droite du centre et les\(2\) unités situées au-dessus et en dessous du centre.
    Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle.
    Marquez les sommets.
    Tracez les branches.    		 .
    Tableau 11.4.7
    Exercice\(\PageIndex{9}\)
    1. Écrivez l'équation sous forme standard et
    2. Graphe\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\).
    Réponse
    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
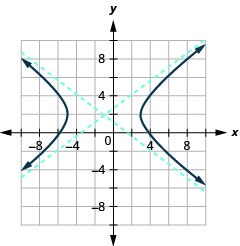
    Le graphique montre les axes x et y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec le centre (négatif 1, 2), une asymptote qui passe par (négatif 5, 5) et (3, négatif 1) et une asymptote qui passe par (3, 5) et (négatif 5, négatif 1), et des branches qui passe par les sommets (négatif 5, 2) et (3, 2) et s'ouvre à gauche et à droite.
    Graphique 11.4.31
    Exercice\(\PageIndex{10}\)
    1. Écrivez l'équation sous forme standard et
    2. Graphe\(16 x^{2}-25 y^{2}+96 x-50 y-281=0\).
    Réponse
    1. \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
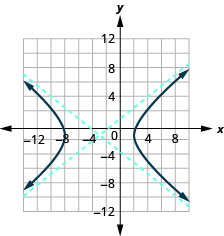
    Le graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés, avec le centre (négatif 3, négatif 1), une asymptote qui passe par (négatif 8, négatif 5) et (2, 3) et une asymptote qui passe par (négatif 8, 3) et (2, négatif 5), et branches qui passent par les sommets (négatif 8, négatif 1) et (2, négatif 1) et s'ouvrent à gauche et à droite.
    Graphique 11.4.32

    Identifier les sections coniques par leurs équations

    Maintenant que nous avons terminé notre étude des sections coniques, nous allons examiner les différentes équations et identifier certaines manières d'identifier une conique par son équation. Lorsque l'on nous donne une équation à représenter graphiquement, il est utile d'identifier la conique afin de savoir quelles sont les prochaines étapes à suivre.

    Pour identifier une conique à partir de son équation, il est plus facile de placer les termes variables d'un côté de l'équation et les constantes de l'autre.

    Conique Caractéristiques des\(x^{2}\) termes et\(y^{2}\) des termes Exemple
    Parabole \ (x^ {2} \) - et\(y^{2}\) -Terms">SOIT\(x^{2}\) OU\(y^{2}\). Une seule variable est mise au carré. \(x=3 y^{2}-2 y+1\)
    cercle Les termes \ (x^ {2} \) - et\(y^{2}\) -terms">\(x^{2}\)\(y^{2}\) - et - ont les mêmes coefficients. \(x^{2}+y^{2}=49\)
    Ellipse Les termes \ (x^ {2} \) - et\(y^{2}\) -terms">\(x^{2}\) - et\(y^{2}\) - ont le même signe, des coefficients différents. \(4 x^{2}+25 y^{2}=100\)
    Hyperbole Les termes \ (x^ {2} \) - et\(y^{2}\) -terms">\(x^{2}\)\(y^{2}\) - et - ont des signes et des coefficients différents. \(25 y^{2}-4 x^{2}=100\)
    Tableau 11.4.8
    Exemple\(\PageIndex{6}\)

    Identifiez le graphique de chaque équation sous la forme d'un cercle, d'une parabole, d'une ellipse ou d'une hyperbole.

    1. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    2. \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
    3. \(x^{2}+y^{2}-6 x-8 y=0\)
    4. \(y=-2 x^{2}-4 x-5\)

    Solution :

    a. Les\(y^{2}\) termes\(x^{2}\) - et -ont le même signe et des coefficients différents.

    \(9 x^{2}+4 y^{2}+56 y+160=0\)

    Ellipse

    b. Les\(y^{2}\) termes\(x^{2}\) - et - ont des signes et des coefficients différents.

    \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)

    Hyperbole

    c. Les\(y^{2}\) termes\(x^{2}\) - et -ont les mêmes coefficients.

    \(x^{2}+y^{2}-6 x-8 y=0\)

    cercle

    d. Une seule variable,\(x\), est mise au carré.

    \(y=-2 x^{2}-4 x-5\)

    Parabole

    Exercice\(\PageIndex{11}\)

    Identifiez le graphique de chaque équation sous la forme d'un cercle, d'une parabole, d'une ellipse ou d'une hyperbole.

    1. \(x^{2}+y^{2}-8 x-6 y=0\)
    2. \(4 x^{2}+25 y^{2}=100\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(16 y^{2}-9 x^{2}=144\)
    Réponse
    1. cercle
    2. Ellipse
    3. Parabole
    4. Hyperbole
    Exercice\(\PageIndex{12}\)

    Identifiez le graphique de chaque équation sous la forme d'un cercle, d'une parabole, d'une ellipse ou d'une hyperbole.

    1. \(16 x^{2}+9 y^{2}=144\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(x^{2}+y^{2}+2 x+6 y+9=0\)
    4. \(4 x^{2}-16 y^{2}=64\)
    Réponse
    1. Ellipse
    2. Parabole
    3. cercle
    4. Hyperbole

    Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les hyperboles.

    • Tracez une hyperbole avec le centre à l'origine
    • Tracez une hyperbole dont le centre n'est pas à l'origine
    • Représenter graphiquement une hyperbole sous forme générale
    • Identification des sections coniques sous forme générale

    Concepts clés

    • Hyperbole : Une hyperbole est l'ensemble des points d'un plan où la différence de leurs distances par rapport à deux points fixes est constante.
    La figure montre un cône circulaire droit à double emboîtement tranché par un plan parallèle à l'axe vertical du cône formant une hyperbole. La figure est intitulée « hyperbole ».
    Graphique 11.4.1
    • Chacun des points fixes est appelé foyer de l'hyperbole.
      La ligne passant par les foyers s'appelle l'axe transversal.
      Les deux points où l'axe transversal croise l'hyperbole sont chacun un sommet de l'hyperbole.
      Le milieu du segment joignant les foyers est appelé le centre de l'hyperbole.
      La ligne perpendiculaire à l'axe transversal qui passe par le centre est appelée axe conjugué.
      Chaque élément du graphique est appelé une branche de l'hyperbole.
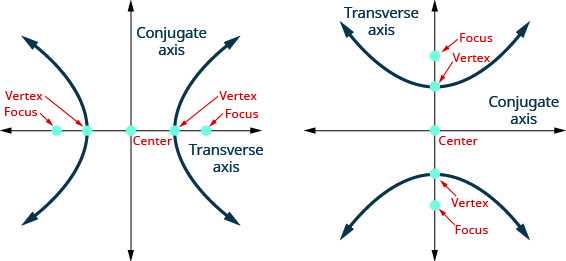
      La figure montre deux graphiques d'une hyperbole. Le premier graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets et les foyers sont représentés par des points situés sur l'axe transversal, qui est l'axe X. Les branches passent par les sommets et s'ouvrent à gauche et à droite. L'axe Y est l'axe conjugué. Le deuxième graphique montre les axes X et Y qui s'étendent tous deux dans les directions négative et positive, mais à des intervalles non étiquetés. Le centre de l'hyperbole est l'origine. Les sommets et les foyers sont représentés par des points situés sur l'axe transversal, qui est l'axe y. Les branches passent par les sommets et s'ouvrent de haut en bas. L'axe X est l'axe conjugué.

    Graphique 11.4.2

    Formes standard de l'équation : une hyperbole avec un centre\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    Orientation \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >Axe transversal sur l'\(x\)axe.
    S'ouvre à gauche et à droite    		 \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >Axe transversal sur l'\(y\)axe.
    S'ouvre de haut en bas
    Sommets \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >\((0,-a),(0, a)\)
    \(x\)-intercepte \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >aucun
    \(y\)-intercepte \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >aucun \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >\((0,-a),(0, a)\)
    Rectangle \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >Utiliser\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >Utiliser\((0, \pm a)( \pm b, 0)\)
    Asymptomtotes \ (\ frac {x^ {2}} {a^ {2}} - \ frac {y^ {2}} {b^ {2}} =1 \) « >\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}} - \ frac {x^ {2}} {b^ {2}} =1 \) « >\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    Tableau 11.4.1
    • Comment représenter graphiquement une hyperbole centrée sur\((0,0)\).
      1. Écrivez l'équation sous forme standard.
      2. Déterminez si l'axe transversal est horizontal ou vertical.
      3. Trouvez les sommets.
      4. Esquissez le rectangle centré à l'origine en coupant un axe à\(±a\) et l'autre à\(±b\).
      5. Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle.
      6. Dessine les deux branches de l'hyperbole.

    Formes standard de l'équation : une hyperbole avec un centre\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    Orientation \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >L'axe transversal est horizontal. S'ouvre à gauche et à droite \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >L'axe transversal est vertical. S'ouvre de haut en bas
    Centre \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >\((h,k)\) \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >\((h,k)\)
    Sommets \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >\(a\) unités à gauche et à droite du centre \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >\(a\) unités au-dessus et en dessous du centre
    Rectangle \ (\ frac {(x-h) ^ {2}} {a^ {2}} - \ frac {(y-k) ^ {2}} {b^ {2}} =1 \) « >Utiliser les\(a\) unités gauche/droite des\(b\) unités centrales au-dessus ou en dessous du centre \ (\ frac {(y-k) ^ {2}} {a^ {2}} - \ frac {(x-h) ^ {2}} {b^ {2}} =1 \) « >Utiliser les\(a\) unités au-dessus ou en dessous des\(b\) unités centrales gauche/droite du centre
    Tableau 11.4.4
    • Comment représenter graphiquement une hyperbole centrée sur\((h,k)\).
      1. Écrivez l'équation sous forme standard.
      2. Déterminez si l'axe transversal est horizontal ou vertical.
      3. Trouvez le centre et\(a,b\).
      4. Esquissez le rectangle centré lors de\((h,k)\) l'utilisation\(a,b\).
      5. Esquissez les asymptotes, c'est-à-dire les lignes traversant les diagonales du rectangle. Marquez les sommets.
      6. Dessine les deux branches de l'hyperbole.
    Conique Caractéristiques des\(x^{2}\) termes et\(y^{2}\) des termes Exemple
    Parabole \ (x^ {2} \) - et\(y^{2}\) -Terms">SOIT\(x^{2}\) OU\(y^{2}\). Une seule variable est mise au carré. \(x=3 y^{2}-2 y+1\)
    cercle Les termes \ (x^ {2} \) - et\(y^{2}\) -terms">\(x^{2}\)\(y^{2}\) - et - ont les mêmes coefficients. \(x^{2}+y^{2}=49\)
    Ellipse Les termes \ (x^ {2} \) - et\(y^{2}\) -terms">\(x^{2}\) - et\(y^{2}\) - ont le même signe, des coefficients différents. \(4 x^{2}+25 y^{2}=100\)
    Hyperbole Les termes \ (x^ {2} \) - et\(y^{2}\) -terms">\(x^{2}\)\(y^{2}\) - et - ont des signes et des coefficients différents. \(25 y^{2}-4 x^{2}=100\)
    Tableau 11.4.8

    Lexique

    hyperbole
    Une hyperbole est définie comme l'ensemble des points d'un plan où la différence de leurs distances par rapport à deux points fixes est constante.