11.3 : Paraboles

Last updated
Save as PDF

Page ID: 194470

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

Tracez des paraboles verticales
Tracez des paraboles horizontales
Résoudre des applications avec des paraboles

Soyez prêt

Avant de commencer, répondez à ce questionnaire de préparation.

Graphique :$y=-3 x^{2}+12 x-12$.
Si vous avez oublié ce problème, consultez l'exemple 9.47.
Résolvez en complétant le carré :$x^{2}-6 x+6=0$.
Si vous avez oublié ce problème, consultez l'exemple 9.12.
Écrivez sous forme standard :$y=3 x^{2}-6 x+5$
Si vous avez oublié ce problème, consultez l'exemple 9.59.

Diagramme de paraboles verticales

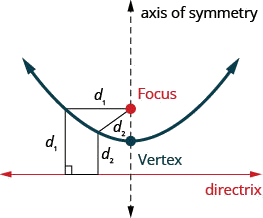
La prochaine section conique que nous allons examiner est une parabole. Nous définissons une parabole comme tous les points d'un plan qui se trouvent à la même distance d'un point fixe et d'une ligne fixe. Le point fixe est appelé foyer et la ligne fixe est appelée directrice de la parabole.

Cette figure montre un double cône. La nappe inférieure est coupée par un plan de telle sorte que l'intersection forme une parabole. — Graphique 11.2.1

Définition$\PageIndex{1}$: Parabola, Focus, and Directrix

Une parabole est constituée de tous les points d'un plan situés à la même distance d'un point fixe et d'une ligne fixe. Le point fixe est appelé foyer et la ligne fixe est appelée directrice de la parabole.

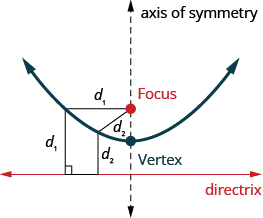
Cette figure montre une parabole s'ouvrant vers le haut. Sous la parabole se trouve une ligne horizontale nommée directrix. Une ligne pointillée verticale passant par le centre de la parabole est appelée axe de symétrie. Le point d'intersection de l'axe avec la parabole est appelé sommet. Un point situé sur l'axe, à l'intérieur de la parabole, est désigné comme point focal. Une ligne perpendiculaire à la directrice relie la directrice à un point de la parabole et une autre droite relie ce point au point focal. Ces deux lignes ont la même longueur. — Graphique 11.2.2

Auparavant, nous avons appris à représenter graphiquement des paraboles verticales à partir du formulaire général ou du formulaire standard à l'aide de propriétés. Ces méthodes fonctionneront également ici. Nous allons résumer les propriétés ici.

Paraboles verticales

Tableau 11.2.1
	Formulaire général $y=a x^{2}+b x+c$	Formulaire standard $y=a(x-h)^{2}+k$
Orientation	\ (y=a x^ {2} +b x+c \) « >$a>0$ haut ;$a<0$ bas	\ (y=a (x-h) ^ {2} +k \) « >$a>0$ haut ;$a<0$ bas
Axe de symétrie	\ (y=a x^ {2} +b x+c \) « >$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k \) « >$x=h$
Sommet	\ (y=a x^ {2} +b x+c \) « >Remplacez$x=-\dfrac{b}{2 a}$ et résolvez par$y .$	\ (y=a (x-h) ^ {2} +k \) « >$(h, k)$
$y$-intercepter	\ (y=a x^ {2} +b x+c \) « >Laissez$x=0$	\ (y=a (x-h) ^ {2} +k \) « >Laissez$x=0$
$x$-intercepte	\ (y=a x^ {2} +b x+c \) « >Laissez$y=0$	\ (y=a (x-h) ^ {2} +k \) « >Laissez$y=0$

Les graphiques montrent à quoi ressemblent les paraboles lorsqu'elles s'ouvrent vers le haut ou vers le bas. Leur position par rapport à l'axe$x$ - ou à$y$ l'axe - n'est qu'un exemple.

Cette figure montre deux paraboles dont l'axe x est égal à h et le sommet h, k. Celle de gauche s'ouvre et A est supérieur à 0. Celui de droite s'ouvre vers le bas. Ici, A est inférieur à 0. — Graphique 11.2.3

Pour représenter graphiquement une parabole à partir de ces formes, nous avons utilisé les étapes suivantes.

Représentation graphique de paraboles verticales

Comment représenter graphiquement des paraboles verticales$y=a x^{2}+b x+c$ ou$f(x)=a(x-h)^{2}+k$ utiliser les propriétés.

Étape 1 : Déterminez si la parabole s'ouvre vers le haut ou vers le bas.
Étape 2 Trouvez l'axe de symétrie.
Étape 3 Trouve le sommet.
Étape 4. Trouvez le$y$ -intercept. Trouvez le point symétrique par rapport à l'$y$intersection -sur l'axe de symétrie.
Étape 5. Trouvez les$x$ -intercepts.
Étape 6. Tracez la parabole.

L'exemple suivant passe en revue la méthode de représentation graphique d'une parabole à partir de la forme générale de son équation.

Exemple$\PageIndex{1}$

$y=-x^{2}+6 x-8$Tracez à l'aide de propriétés

Solution :

Tableau 11.2.2
	$ \begin{align} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt] \color{black}{y} &=-x^{2}+6 x-8 \end{align}$
Depuis lors$a$$-1$, la parabole s'ouvre vers le bas.
$.$
Pour trouver l'axe de symétrie, trouvez$x=-\dfrac{b}{2 a}$.	$ \begin{align} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align}$
	L'axe de symétrie est$x=3$.
	$.$
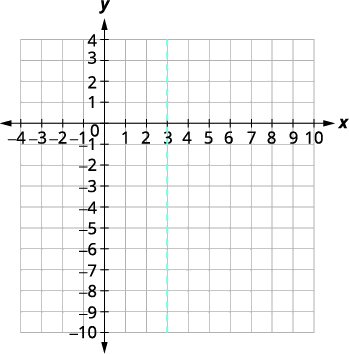Le sommet se trouve sur la ligne$x=3$.	$y=-x^{2}+6 x-8$
Laissez$x=3$.	$.$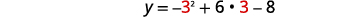
	$\begin{align} y &=-9+18-8 \\[4pt] y &=1 \end{align}$
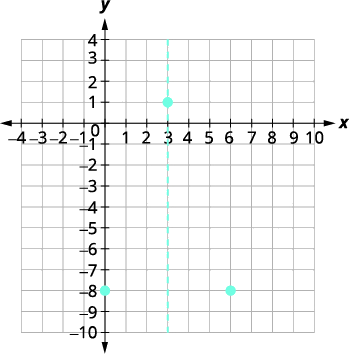
	Le sommet est$(3,1)$.
	$.$
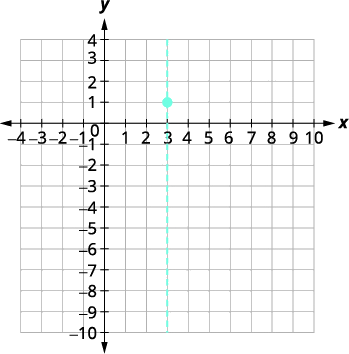Le$y$ -intercept se produit lorsque$x=0$.	$y=-x^{2}+6 x-8$
Substitut$x=0$.	$y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8$
Simplifiez.	$y=-8$
	Le$y$ -intercept est$(0,-8)$.
Le point$(0,−8)$ se trouve à trois unités à gauche de la ligne de symétrie. Le point situé à trois unités à droite de la ligne de symétrie est$(6,−8)$.	Le point symétrique par rapport à l'$y$-intercept est$(6,−8)$.
	$.$
Le$x$ -intercept se produit lorsque$y=0$.	$y=-x^{2}+6 x-8$
Laissez$y=0$.	$\color{red}{0} \color{black}{=}-x^{2}+6 x-8$
Tenez compte du GCF.	$0=-\left(x^{2}-6 x+8\right)$
Tenez compte du trinôme.	$0=-(x-4)(x-2)$
Résolvez pour$x$.	$x=4, \quad x=2$
	Les$x$ -intercepts sont$(4,0),(2,0)$.
Tracez la parabole.	$.$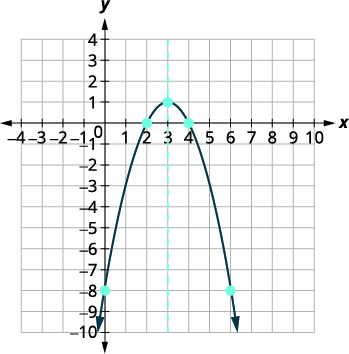

Exercice$\PageIndex{1}$

$y=-x^{2}+5 x-6$Tracez à l'aide de propriétés

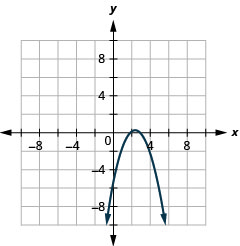
Réponse: $Ce graphique montre une parabole s'ouvrant vers le bas, avec x interceptions (2, 0) et (3, 0) et une intersection y (0, négatif 6).$
Graphique 11.2.24

Exercice$\PageIndex{2}$

$y=-x^{2}+8 x-12$Tracez à l'aide de propriétés

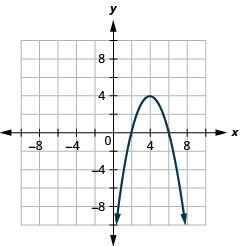
Réponse: $Ce graphique montre une parabole s'ouvrant vers le bas, avec un sommet (4, 4) et des points d'intersection x (2, 0) et (6, 0).$
Graphique 11.2.25

L'exemple suivant passe en revue la méthode de représentation graphique d'une parabole à partir de la forme standard de son équation,$y=a(x-h)^{2}+k$.

Exemple$\PageIndex{2}$

Écrivez$y=3 x^{2}-6 x+5$ sous forme standard, puis utilisez les propriétés de la forme standard pour représenter graphiquement l'équation.

Solution :

Tableau 11.2.3
Réécrivez la fonction$y=a(x-h)^{2}+k$ sous forme en complétant le carré.	$\begin{align} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3 \\[4pt] y &=3(x-1)^{2}+2 \end{align}$
Identifiez les constantes$a, h, k$.	$a=3, h=1, k=2$
Depuis$a=2$, la parabole s'ouvre vers le haut.
$.$
L'axe de symétrie est$x=h$.	L'axe de symétrie est$x=1$.
Le sommet est$(h,k)$.	Le sommet est$(1,2)$.
Trouvez le$y$ -intercept en le remplaçant$x=0$ par	$ \begin{align} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align} $
	$y$-intercepter$(0,5)$
Trouvez le point symétrique par rapport à$(0,5)$ l'axe de symétrie.	$(2,5)$
Trouvez les$x$ -intercepts.	$\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}$
	La racine carrée d'un nombre négatif nous indique que les solutions sont des nombres complexes. Il n'y a donc pas$x$ d'interception.
Tracez la parabole.	$.$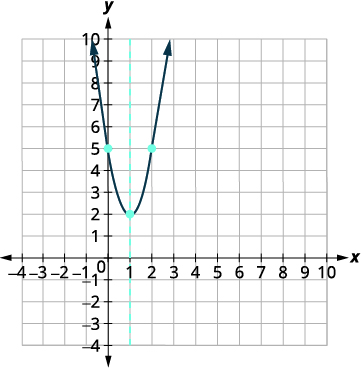

Exercice$\PageIndex{3}$

Écrivez$y=2 x^{2}+4 x+5$ sous forme standard et
utilisez les propriétés de la forme standard pour représenter graphiquement l'équation.

Réponse

$y=2(x+1)^{2}+3$

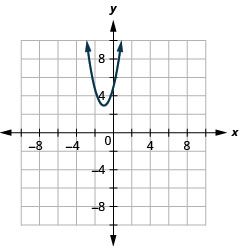
Ce graphique montre une parabole s'ouvrant vers le haut, avec un sommet (négatif 1, 3) et une intersection y (0, 5). Il y a le point moins (2, 5) dessus. — Graphique 11.2.28

Exercice$\PageIndex{4}$

Écrivez$y=-2 x^{2}+8 x-7$ sous forme standard et
utilisez les propriétés de la forme standard pour représenter graphiquement l'équation.

Réponse

$y=-2(x-2)^{2}+1$

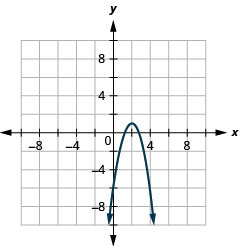
Ce graphique montre une parabole s'ouvrant vers le bas, avec le sommet (2, 1) et l'axe de symétrie x égal à 2. Son intersection y est (0, moins 7). — Graphique 11.2.29

Diagramme de paraboles horizontales

Jusqu'à présent, notre travail n'a porté que sur les paraboles qui s'ouvrent vers le haut ou vers le bas. Nous allons maintenant examiner les paraboles horizontales. Ces paraboles s'ouvrent soit vers la gauche soit vers la droite. Si nous échangeons les$x$ et$y$ de nos équations précédentes contre des paraboles, nous obtenons les équations des paraboles qui s'ouvrent vers la gauche ou vers la droite.

Paraboles horizontales

Tableau 11.2.4
	Formulaire général $x=a y^{2}+b y+c$	Formulaire standard $x=a(y-k)^{2}+h$
Orientation	\ (x=a y^ {2} +b y+c \) « >$a>0$ droite ;$a<0$ gauche	\ (x=a (y-k) ^ {2} +h \) « >$a>0$ droite ;$a<0$ gauche
Axe de symétrie	\ (x=a y^ {2} +b y+c \) « >$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h \) « >$y=k$
Sommet	\ (x=a y^ {2} +b y+c \) « >Remplacez$y=-\dfrac{b}{2 a}$ et résolvez par$x .$	\ (x=a (y-k) ^ {2} +h \) « >$(h, k)$
$x$-intercepte	\ (x=a y^ {2} +b y+c \) « >Laisser$x=0$	\ (x=a (y-k) ^ {2} +h \) « >Laissez$x=0$
$y$-intercepter	\ (x=a y^ {2} +b y+c \) « >Laisser$y=0$	\ (x=a (y-k) ^ {2} +h \) « >Laissez$y=0$

Les graphiques montrent à quoi ressemblent les paraboles lorsqu'elles se trouvent à gauche ou à droite. Leur position par rapport à l'axe$x$ - ou à$y$ l'axe - n'est qu'un exemple.

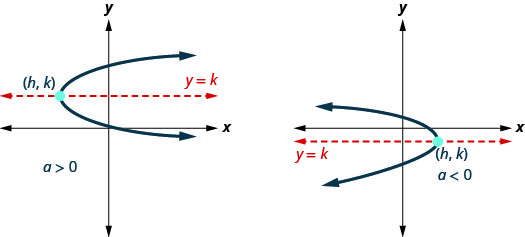
Cette figure montre deux paraboles dont l'axe de symétrie y est égal à k,) et le sommet (h, k). La parabole de gauche est étiquetée supérieure à 0 et s'ouvre vers la droite. L'autre parabole s'ouvre vers la gauche. — Graphique 11.2.30

En regardant ces paraboles, leurs graphes représentent-ils une fonction ? Comme les deux graphes échoueraient au test de la ligne verticale, ils ne représentent pas une fonction.

Tracer une parabole qui s'ouvre vers la gauche ou vers la droite est fondamentalement identique à ce que nous avons fait pour les paraboles qui s'ouvrent vers le haut ou vers le bas, avec l'inversion des$y$ variables$x$ et.

Comment : représenter graphiquement des paraboles horizontales$y=a x^{2}+b x+c$ or $f(x)=a(x-h)^{2}+k$ using Properties

Étape 1 : Déterminez si la parabole s'ouvre vers la gauche ou vers la droite.
Étape 2 : Trouvez l'axe de symétrie
Étape 3 : Trouvez le sommet
Étape 4 : Trouvez le$x$ -intercept. Trouvez le point symétrique par rapport à l'$x$intersection -sur l'axe de symétrie.
Étape 5 : Trouvez les$y$ -intercepts.
Étape 6 : Tracez la parabole.

Exemple$\PageIndex{3}$

$x=2 y^{2}$Tracez à l'aide de propriétés

Solution :

Tableau 11.2.5
	$.$
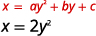Depuis$a=2$, la parabole s'ouvre vers la droite.
$.$
Pour trouver l'axe de symétrie, trouvez$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{0}{2(2)}$
	$y=0$
	L'axe de symétrie est$y=0$.
Le sommet se trouve sur la ligne$y=0$.	$x=2 y^{2}$
Laissez$y=0$.	$.$
	$x=0$
	Le sommet est$(0,0)$.

Puisque le sommet est$(0,0)$, les$y$ interceptions$x$ - et -sont toutes deux le point$(0,0)$. Pour représenter graphiquement la parabole, nous avons besoin de plus de points. Dans ce cas, il est plus facile de choisir des valeurs de$y$.

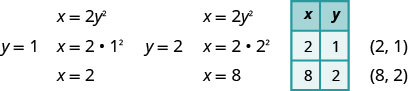
Dans l'équation, x est égal à 2 y au carré, lorsque y est égal à 1, x est 2 et lorsque y est égal à 2, x est 8. Les points sont (2, 1) et (8, 2). — Graphique 11.2.38

Nous tracons également les points symétriquement par rapport à l'$y$axe$(2,1)$ -et à$(8,2)$ travers celui-ci, les points$(2,−1),(8,−2)$.

Tracez la parabole.

Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (0, 0). Quatre points y sont marqués : point (2, 1), point (2, moins 1), point (8, 2) et point (8 moins 2). — Graphique 11.2.39

Exercice$\PageIndex{5}$

$x=y^{2}$Tracez à l'aide de propriétés

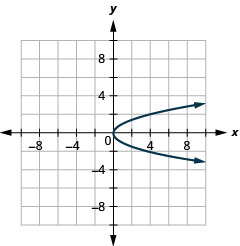
Réponse: $Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet à l'origine. Deux points sont (4, 2) et (4, moins 2).$
Graphique 11.2.40

Exercice$\PageIndex{6}$

$x=-y^{2}$Tracez à l'aide de propriétés

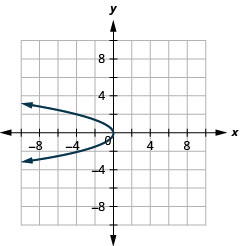
Réponse: $Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet à l'origine. Deux points sont (négatif 4, 2) et (négatif 4, négatif 2).$
Graphique 11.2.41

Dans l'exemple suivant, le sommet n'est pas l'origine.

Exemple$\PageIndex{4}$

$x=-y^{2}+2 y+8$Tracez à l'aide de propriétés

Solution :

Tableau 11.2.6
	$.$
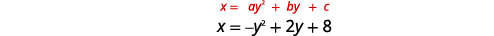Depuis$a=-1$, la parabole s'ouvre vers la gauche.
$.$
Pour trouver l'axe de symétrie, trouvez$y=-\dfrac{b}{2 a}$	$y=-\dfrac{b}{2 a}$
	$y=-\dfrac{2}{2(-1)}$
	$y=1$
	L'axe de symétrie est$y=1$.
Le sommet se trouve sur la ligne$y=1$.	$x=-y^{2}+2 y+8$
Laissez$y=1$.	$.$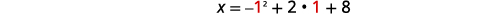
	$x=9$
	Le sommet est$(9,1)$.
Le$x$ -intercept se produit lorsque$y=0$.	$x=-y^{2}+2 y+8$
	$.$
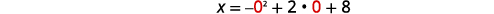	$x=8$
	Le$x$ -intercept est$(8,0)$.
Le point$(8,0)$ se trouve à une unité en dessous de la ligne de symétrie. Le point symétrique situé à une unité au-dessus de la ligne de symétrie est$(8,2)$	Le point symétrique est$(8,2)$.
Le$y$ -intercept se produit lorsque$x=0$.	$x=-y^{2}+2 y+8$
Substitut$x=0$.	$0=-y^{2}+2 y+8$
Résoudre.	$y^{2}-2 y-8=0$
	$(y-4)(y+2)=0$
	$y=4, \quad y=-2$
	Les$y$ -intercepts sont$(0,4)$ et$(0,-2)$.
Reliez les points pour représenter graphiquement la parabole.	$.$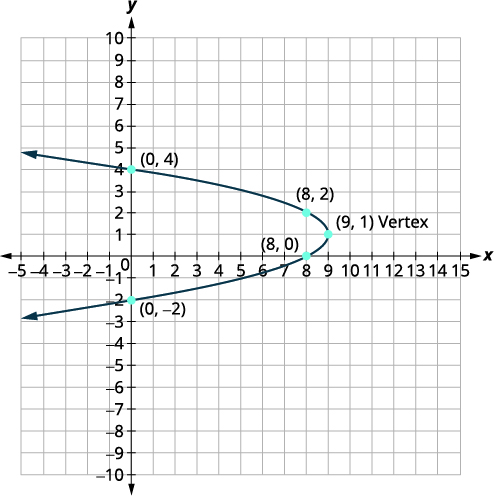

Exercice$\PageIndex{7}$

$x=-y^{2}-4 y+12$Tracez à l'aide de propriétés

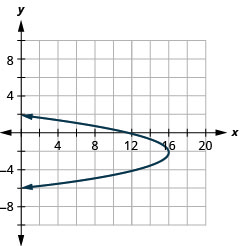
Réponse: $Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (16, négatif 2) et une intersection en X (12, 0).$
Graphique 11.2.58

Exercice$\PageIndex{8}$

$x=-y^{2}+2 y-3$Tracez à l'aide de propriétés

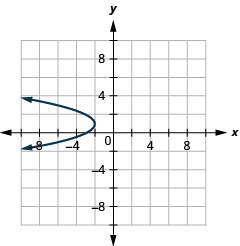
Réponse: $Ce graphique montre une parabole d'ouverture gauche avec un sommet (négatif 2, 1) et une intersection x moins (3, 0).$
Graphique 11.2.59

Dans le tableau 11.2.4, nous voyons la relation entre l'équation sous forme standard et les propriétés de la parabole. La zone Comment faire répertorie les étapes à suivre pour représenter graphiquement une parabole dans le formulaire standard$x=a(y-k)^{2}+h$. Nous utiliserons cette procédure dans l'exemple suivant.

Exemple$\PageIndex{5}$

Graphe$x=2(y-2)^{2}+1$ à l'aide de propriétés

Solution :

Tableau 11.2.7
	$.$
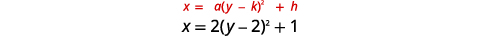Identifiez les constantes$a, h, k$.	$a=2, h=1, k=2$
Depuis$a=2$, la parabole s'ouvre vers la droite.
$.$
L'axe de symétrie est$y=k$.	L'axe de symétrie est$y=2$.
Le sommet est$(h,k)$.	Le sommet est$(1,2)$.
Trouvez le$x$ -intercept en le remplaçant$y=0$.	$x=2(y-2)^{2}+1$ $x=2(0-2)^{2}+1$ $x=9$
	Le$x$ -intercept est$(9,0)$.
Trouvez le point symétrique par rapport à$(9,0)$ l'axe de symétrie.	$(9,4)$
Trouvez les$y$ -intercepts. Laissez$x=0$.	$\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}$
	Un carré ne peut pas être négatif, il n'y a donc pas de véritable solution. Il n'y a donc pas$y$ d'interception.
Tracez la parabole.	$.$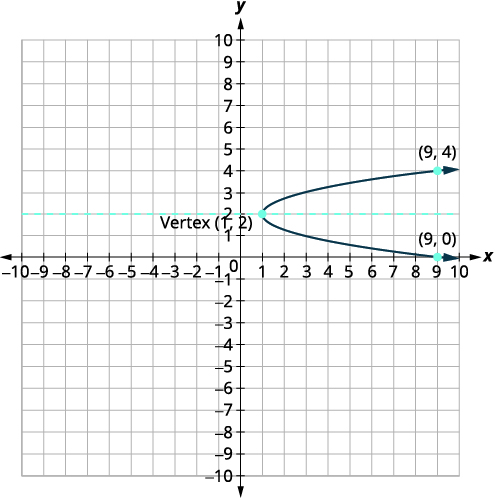

Exercice$\PageIndex{9}$

Graphe$x=3(y-1)^{2}+2$ à l'aide de propriétés

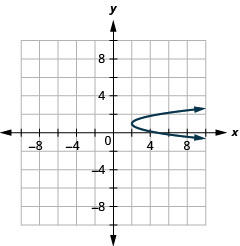
Réponse: $Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (2, 1) et une intersection en x (5, 0).$
Graphique 11.2.63

Exercice$\PageIndex{10}$

Graphe$x=2(y-3)^{2}+2$ à l'aide de propriétés

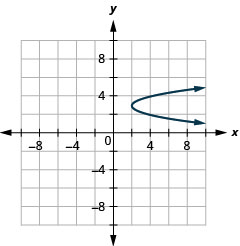
Réponse: $Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (2, 3) et des points symétriques (4, 2) et (4, 4).$
Graphique 11.2.64

Dans l'exemple suivant, nous remarquons que le a est négatif et que la parabole s'ouvre vers la gauche.

Exemple$\PageIndex{6}$

Graphe$x=-4(y+1)^{2}+4$ à l'aide de propriétés

Solution :

Tableau 11.2.8
	$.$
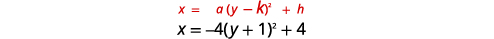Identifiez les constantes$a, h, k$.	$a=-4, h=4, k=-1$
Depuis$a=-4$, la parabole s'ouvre vers la gauche.
$.$
L'axe de symétrie est$y=k$.	L'axe de symétrie est$y=-1$.
Le sommet est$(h,k)$.	Le sommet est$(4,-1)$.
Trouvez le$x$ -intercept en le remplaçant$y=0$.	$x=-4(y+1)^{2}+4$ $x=-4(0+1)^{2}+4$ $x=0$
	Le$x$ -intercept est$(0,0)$.
Trouvez le point symétrique par rapport à$(0,0)$ l'axe de symétrie.	$(0,-2)$
Trouvez les$y$ -intercepts.	$x=-4(y+1)^{2}+4$
Laissez$x=0$.	$\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}$
	$y=-1+1 \quad y=-1-1$
	$y=0 \quad\quad y=-2$
	Les$y$ -intercepts sont$(0,0)$ et$(0,-2)$.
Tracez la parabole.	$.$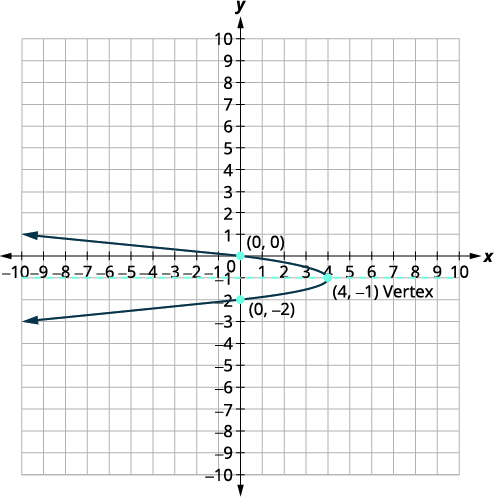

Exercice$\PageIndex{11}$

Graphe$x=-4(y+2)^{2}+4$ à l'aide de propriétés

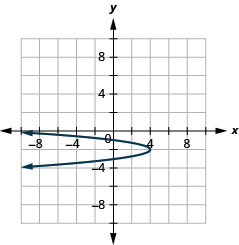
Réponse: $Cette figure montre une parabole s'ouvrant vers la gauche avec un sommet (4, négatif 2) et des intersections y (0, négatif 1) et (0, négatif 3).$
Graphique 11.2.68

Exercice$\PageIndex{12}$

Graphe$x=-2(y+3)^{2}+2$ à l'aide de propriétés

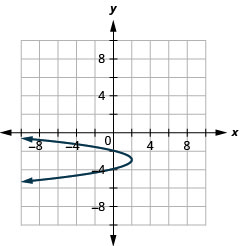
Réponse: $Cette figure montre une parabole s'ouvrant vers la gauche avec un sommet (2, négatif 3) et des intersections y (0, négatif 2) et (0, négatif 4).$
Graphique 11.2.69

L'exemple suivant exige que nous mettions d'abord l'équation sous forme standard, puis que nous utilisions les propriétés.

Exemple$\PageIndex{7}$

Écrivez$x=2 y^{2}+12 y+17$ sous forme standard, puis utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.

Solution :

Tableau 11.2.9
	$x=2 y^{2}+12 y+17$
Réécrivez la fonction$x=a(y-k)^{2}+h$ sous forme en complétant le carré.	$x=2\left(y^{2}+6 y\right)+17$
	$.$
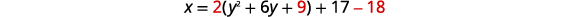	$x=2(y+3)^{2}-1$
	$.$
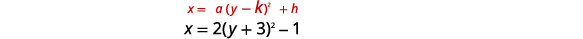Identifiez les constantes$a, h, k$.	$a=2, h=-1, k=-3$
Depuis$a=2$, la parabole s'ouvre vers la droite.
$.$
L'axe de symétrie est$y=k$.	L'axe de symétrie est$y=-3$.
Le sommet est$(h,k)$.	Le sommet est$(-1,-3)$.
Trouvez le$x$ -intercept en le remplaçant$y=0$.	$x=2(y+3)^{2}-1$ $x=2(0+3)^{2}-1$ $x=17$
	Le$x$ -intercept est$(17,0)$.
Trouvez le point symétrique par rapport à$(17,0)$ l'axe de symétrie.	$(17,-6)$
Trouvez les$y$ -intercepts. Laissez$x=0$.	$\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}$
	$y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}$
	$y \approx-2.3 \quad y \approx-3.7$
	Les$y$ -intercepts sont$\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)$.
Tracez la parabole.	$.$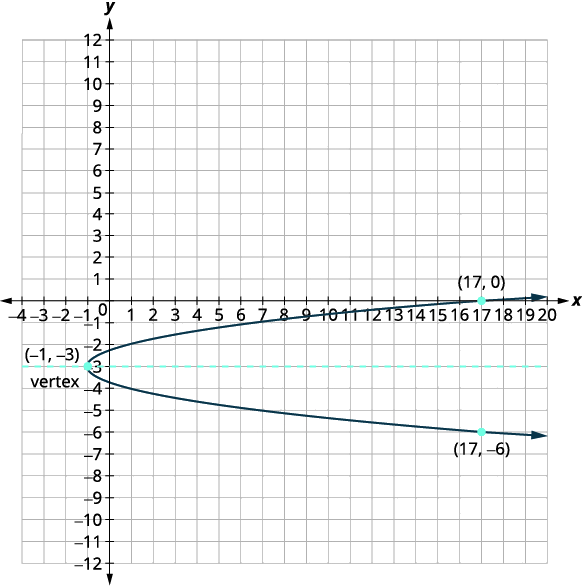

Exercice$\PageIndex{13}$

Écrivez$x=3 y^{2}+6 y+7$ sous forme standard et
Utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.

Réponse

$x=3(y+1)^{2}+4$

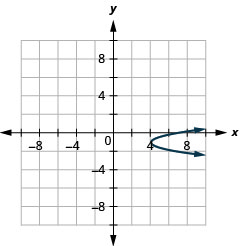
Ce graphique montre une parabole s'ouvrant vers la droite avec un sommet (4, négatif 1) et une intersection x (7, 0). — Graphique 11.2.77

Exercice$\PageIndex{14}$

Écrivez$x=-4 y^{2}-16 y-12$ sous forme standard et
Utilisez les propriétés du formulaire standard pour représenter graphiquement l'équation.

Réponse

$x=-4(y+2)^{2}+4$

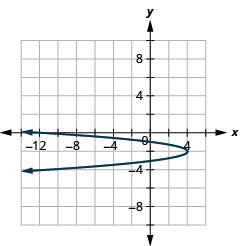
Ce graphique montre une parabole s'ouvrant vers la gauche avec un sommet (4, négatif 2) et une intersection x moins (12, 0). — Graphique 11.2.78

Résoudre des applications avec des paraboles

De nombreuses conceptions architecturales intègrent des paraboles. Il n'est pas rare que des ponts soient construits à l'aide de paraboles comme nous le verrons dans l'exemple suivant.

Exemple$\PageIndex{8}$

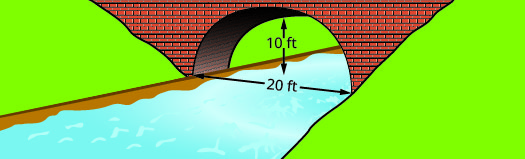
Trouvez l'équation de l'arc parabolique formé dans la fondation du pont illustré. Écrivez l'équation sous forme standard.

Cette figure montre un arc parabolique formé dans les fondations d'un pont. Il mesure 10 pieds de haut et 20 pieds de large à la base. — Graphique 11.2.79

Solution :

Nous allons d'abord mettre en place un système de coordonnées et dessiner la parabole. Le graphique nous donnera les informations dont nous avons besoin pour écrire l'équation du graphique sous la forme standard$y=a(x-h)^{2}+k$.

Tableau 11.2.10
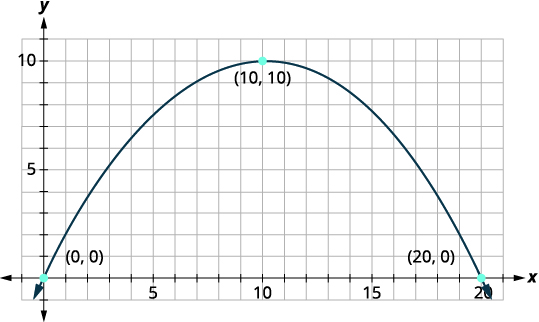Laissez le côté inférieur gauche du pont être l'origine de la grille de coordonnées au point$(0,0)$. Comme la base mesure les$20$ pieds de large, le point$(20,0)$ représente le côté inférieur droit. Le pont mesure 10 pieds de haut au point le plus élevé. Le point le plus élevé est le sommet de la parabole, donc la$y$ coordonnée -du sommet sera$10$. Comme le pont est symétrique, le sommet doit se situer à mi-chemin entre le point le plus à gauche et le point le plus à droite$(20,0)$.$(0,0)$ De là, nous savons que la$x$ coordonnée du sommet sera également$10$.	$.$
Identifiez le sommet,$(h,k)$.	$(h, k)=(10,10)$
	$h=10, \quad k=10$
Remplacez les valeurs dans le formulaire standard. La valeur de$a$ est encore inconnue. Pour trouver la valeur de,$a$ utilisez l'un des autres points de la parabole.	$\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}$
Remplacez les valeurs de l'autre point dans l'équation.	$y=a(x-10)^{2}+10$ $0=a(0-10)^{2}+10$
Résolvez pour$a$.	$\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}$
	$y=a(x-10)^{2}+10$
Remplacez la valeur par$a$ dans l'équation.	$y=-\dfrac{1}{10}(x-10)^{2}+10$

Exercice$\PageIndex{15}$

Trouvez l'équation de l'arc parabolique formé dans la fondation du pont illustré. Écrivez l'équation sous forme standard.

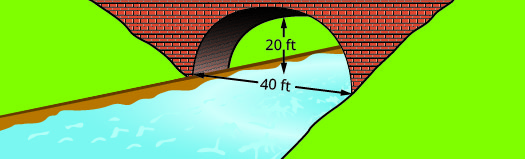
Cette figure montre un arc parabolique formé dans les fondations d'un pont. Il mesure 20 pieds de haut et 40 pieds de large à la base. — Graphique 11.2.81

Réponse: $y=-\dfrac{1}{20}(x-20)^{2}+20$

Exercice$\PageIndex{16}$

Trouvez l'équation de l'arc parabolique formé dans la fondation du pont illustré. Écrivez l'équation sous forme standard.

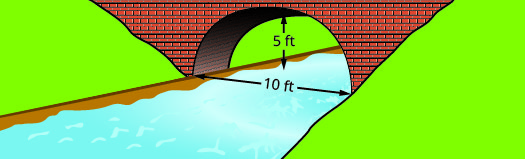
Cette figure montre un arc parabolique formé dans les fondations d'un pont. Il mesure 5 pieds de haut et 10 pieds de large à la base. — Graphique 11.2.82

Réponse: $y=-\dfrac{1}{5} x^{2}+2 x y=-\dfrac{1}{5}(x-5)^{2}+5$

Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à utiliser les fonctions quadratiques et les paraboles.

Fonctions quadratiques
Introduction aux coniques et à la représentation graphique de paraboles horizontales

Concepts clés

Parabole : Une parabole est constituée de tous les points d'un plan situés à la même distance d'un point fixe et d'une ligne fixe. Le point fixe est appelé foyer et la ligne fixe est appelée directrice de la parabole.

Paraboles verticales

Tableau 11.2.1
	Formulaire général $y=a x^{2}+b x+c$	Formulaire standard $y=a(x-h)^{2}+k$
Orientation	\ (y=a x^ {2} +b x+c \) « >$a>0$ haut ;$a<0$ bas	\ (y=a (x-h) ^ {2} +k \) « >$a>0$ haut ;$a<0$ bas
Axe de symétrie	\ (y=a x^ {2} +b x+c \) « >$x=-\dfrac{b}{2 a}$	\ (y=a (x-h) ^ {2} +k \) « >$x=h$
Sommet	\ (y=a x^ {2} +b x+c \) « >Remplacez$x=-\dfrac{b}{2 a}$ et résolvez par$y .$	\ (y=a (x-h) ^ {2} +k \) « >$(h, k)$
$y$-intercepter	\ (y=a x^ {2} +b x+c \) « >Laissez$x=0$	\ (y=a (x-h) ^ {2} +k \) « >Laissez$x=0$
$x$-intercepte	\ (y=a x^ {2} +b x+c \) « >Laissez$y=0$	\ (y=a (x-h) ^ {2} +k \) « >Laissez$y=0$

Comment représenter graphiquement des paraboles verticales$y=a x^{2}+b x+c$ ou$f(x)=a(x-h)^{2}+k)$ utiliser des propriétés

Détermine si la parabole s'ouvre vers le haut ou vers le bas.
Trouvez l'axe de symétrie.
Trouvez le sommet.
Trouvez le$y$ -intercept. Trouvez le point symétrique par rapport à l'$y$intersection -sur l'axe de symétrie.
Trouvez les$x$ -intercepts.
Tracez la parabole.

Paraboles horizontales

Tableau 11.2.4
	Formulaire général $x=a y^{2}+b y+c$	Formulaire standard $x=a(y-k)^{2}+h$
Orientation	\ (x=a y^ {2} +b y+c \) « >$a>0$ droite ;$a<0$ gauche	\ (x=a (y-k) ^ {2} +h \) « >$a>0$ droite ;$a<0$ gauche
Axe de symétrie	\ (x=a y^ {2} +b y+c \) « >$y=-\dfrac{b}{2 a}$	\ (x=a (y-k) ^ {2} +h \) « >$y=k$
Sommet	\ (x=a y^ {2} +b y+c \) « >Remplacez$y=-\dfrac{b}{2 a}$ et résolvez par$x .$	\ (x=a (y-k) ^ {2} +h \) « >$(h, k)$
$x$-intercepte	\ (x=a y^ {2} +b y+c \) « >Laisser$x=0$	\ (x=a (y-k) ^ {2} +h \) « >Laissez$x=0$
$y$-intercepter	\ (x=a y^ {2} +b y+c \) « >Laisser$y=0$	\ (x=a (y-k) ^ {2} +h \) « >Laissez$y=0$

Représentation graphique de paraboles horizontales

Comment représenter graphiquement des paraboles horizontales$x=a y^{2}+b y+c$ ou$x=a(y-k)^{2}+h$ utiliser des propriétés.

Déterminez si la parabole s'ouvre vers la gauche ou vers la droite.
Trouvez l'axe de symétrie.
Trouvez le sommet.
Trouvez le$x$ -intercept. Trouvez le point symétrique par rapport à l'$x$intersection -sur l'axe de symétrie.
Trouvez les$y$ -intercepts.
Tracez la parabole.

Lexique

parabole: Une parabole est constituée de tous les points d'un plan situés à la même distance d'un point fixe et d'une ligne fixe.

	Formulaire général \(y=a x^{2}+b x+c\)	Formulaire standard \(y=a(x-h)^{2}+k\)
Orientation	\ (y=a x^ {2} +b x+c \) « >\(a>0\) haut ;\(a<0\) bas	\ (y=a (x-h) ^ {2} +k \) « >\(a>0\) haut ;\(a<0\) bas
Axe de symétrie	\ (y=a x^ {2} +b x+c \) « >\(x=-\dfrac{b}{2 a}\)	\ (y=a (x-h) ^ {2} +k \) « >\(x=h\)
Sommet	\ (y=a x^ {2} +b x+c \) « >Remplacez\(x=-\dfrac{b}{2 a}\) et résolvez par\(y .\)	\ (y=a (x-h) ^ {2} +k \) « >\((h, k)\)
\(y\)-intercepter	\ (y=a x^ {2} +b x+c \) « >Laissez\(x=0\)	\ (y=a (x-h) ^ {2} +k \) « >Laissez\(x=0\)
\(x\)-intercepte	\ (y=a x^ {2} +b x+c \) « >Laissez\(y=0\)	\ (y=a (x-h) ^ {2} +k \) « >Laissez\(y=0\)

	\( \begin{align} \color{red}{y} &\color{red}{=} a x^{2}+b x+c \\[4pt] \color{black}{y} &=-x^{2}+6 x-8 \end{align}\)
Depuis lors\(a\)\(-1\), la parabole s'ouvre vers le bas.
$.$
Pour trouver l'axe de symétrie, trouvez\(x=-\dfrac{b}{2 a}\).	\( \begin{align} x &=-\dfrac{b}{2 a}\\[4pt] x &=-\dfrac{6}{2(-1)} \\[4pt] x &= 3 \end{align}\)
	L'axe de symétrie est\(x=3\).
	$.$
Le sommet se trouve sur la ligne\(x=3\).	\(y=-x^{2}+6 x-8\)
Laissez\(x=3\).	$.$
	\(\begin{align} y &=-9+18-8 \\[4pt] y &=1 \end{align}\)
	Le sommet est\((3,1)\).
	$.$
Le\(y\) -intercept se produit lorsque\(x=0\).	\(y=-x^{2}+6 x-8\)
Substitut\(x=0\).	\(y=-\color{red}{0}^{\color{black}{2}}+6 \cdot \color{red}{0} \color{black}{-} 8\)
Simplifiez.	\(y=-8\)
	Le\(y\) -intercept est\((0,-8)\).
Le point\((0,−8)\) se trouve à trois unités à gauche de la ligne de symétrie. Le point situé à trois unités à droite de la ligne de symétrie est\((6,−8)\).	Le point symétrique par rapport à l'\(y\)-intercept est\((6,−8)\).
	$.$
Le\(x\) -intercept se produit lorsque\(y=0\).	\(y=-x^{2}+6 x-8\)
Laissez\(y=0\).	\(\color{red}{0} \color{black}{=}-x^{2}+6 x-8\)
Tenez compte du GCF.	\(0=-\left(x^{2}-6 x+8\right)\)
Tenez compte du trinôme.	\(0=-(x-4)(x-2)\)
Résolvez pour\(x\).	\(x=4, \quad x=2\)
	Les\(x\) -intercepts sont\((4,0),(2,0)\).
Tracez la parabole.	$.$

Réécrivez la fonction\(y=a(x-h)^{2}+k\) sous forme en complétant le carré.	\(\begin{align} y &=3 x^{2}-6 x+5 \\[4pt] y &=3\left(x^{2}-2 x\right)+5 \\[4pt] y &=3\left(x^{2}-2 x+1\right) + 5-3 \\[4pt] y &=3(x-1)^{2}+2 \end{align}\)
Identifiez les constantes\(a, h, k\).	\(a=3, h=1, k=2\)
Depuis\(a=2\), la parabole s'ouvre vers le haut.
$.$
L'axe de symétrie est\(x=h\).	L'axe de symétrie est\(x=1\).
Le sommet est\((h,k)\).	Le sommet est\((1,2)\).
Trouvez le\(y\) -intercept en le remplaçant\(x=0\) par	\( \begin{align} y &=3(x-1)^{2}+2 \\[4pt] y &=3 \cdot 0^{2}-6 \cdot 0+5 \\[4pt] y &=0 \end{align} \)
	\(y\)-intercepter\((0,5)\)
Trouvez le point symétrique par rapport à\((0,5)\) l'axe de symétrie.	\((2,5)\)
Trouvez les\(x\) -intercepts.	\(\begin{aligned} y &=3(x-1)^{2}+2 \\[4pt] 0 &=3(x-1)^{2}+2 \\[4pt] -2 &=3(x-1)^{2} \\[4pt] -\dfrac{2}{3} &=(x-1)^{2} \\[4pt] \pm \sqrt{-\dfrac{2}{3}} &=x-1 \end{aligned}\)
	La racine carrée d'un nombre négatif nous indique que les solutions sont des nombres complexes. Il n'y a donc pas\(x\) d'interception.
Tracez la parabole.	$.$

	Formulaire général \(x=a y^{2}+b y+c\)	Formulaire standard \(x=a(y-k)^{2}+h\)
Orientation	\ (x=a y^ {2} +b y+c \) « >\(a>0\) droite ;\(a<0\) gauche	\ (x=a (y-k) ^ {2} +h \) « >\(a>0\) droite ;\(a<0\) gauche
Axe de symétrie	\ (x=a y^ {2} +b y+c \) « >\(y=-\dfrac{b}{2 a}\)	\ (x=a (y-k) ^ {2} +h \) « >\(y=k\)
Sommet	\ (x=a y^ {2} +b y+c \) « >Remplacez\(y=-\dfrac{b}{2 a}\) et résolvez par\(x .\)	\ (x=a (y-k) ^ {2} +h \) « >\((h, k)\)
\(x\)-intercepte	\ (x=a y^ {2} +b y+c \) « >Laisser\(x=0\)	\ (x=a (y-k) ^ {2} +h \) « >Laissez\(x=0\)
\(y\)-intercepter	\ (x=a y^ {2} +b y+c \) « >Laisser\(y=0\)	\ (x=a (y-k) ^ {2} +h \) « >Laissez\(y=0\)

	$.$
Depuis\(a=2\), la parabole s'ouvre vers la droite.
$.$
Pour trouver l'axe de symétrie, trouvez\(y=-\dfrac{b}{2 a}\)	\(y=-\dfrac{b}{2 a}\)
	\(y=-\dfrac{0}{2(2)}\)
	\(y=0\)
	L'axe de symétrie est\(y=0\).
Le sommet se trouve sur la ligne\(y=0\).	\(x=2 y^{2}\)
Laissez\(y=0\).	$.$
	\(x=0\)
	Le sommet est\((0,0)\).

Définition\(\PageIndex{1}\): Parabola, Focus, and Directrix

Représentation graphique de paraboles verticales

Exemple\(\PageIndex{1}\)

Exercice\(\PageIndex{1}\)

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{2}\)

Exercice\(\PageIndex{3}\)

Exercice\(\PageIndex{4}\)

Comment : représenter graphiquement des paraboles horizontales\(y=a x^{2}+b x+c\) or \(f(x)=a(x-h)^{2}+k\) using Properties

Exemple\(\PageIndex{3}\)

Exercice\(\PageIndex{5}\)

Exercice\(\PageIndex{6}\)

Exemple\(\PageIndex{4}\)

Exercice\(\PageIndex{7}\)

Exercice\(\PageIndex{8}\)

Exemple\(\PageIndex{5}\)

Exercice\(\PageIndex{9}\)

Exercice\(\PageIndex{10}\)

Exemple\(\PageIndex{6}\)

Exercice\(\PageIndex{11}\)

Exercice\(\PageIndex{12}\)

Exemple\(\PageIndex{7}\)

Exercice\(\PageIndex{13}\)

Exercice\(\PageIndex{14}\)

Exemple\(\PageIndex{8}\)

Exercice\(\PageIndex{15}\)

Exercice\(\PageIndex{16}\)

Représentation graphique de paraboles horizontales

	$.$
Depuis\(a=-1\), la parabole s'ouvre vers la gauche.
$.$
Pour trouver l'axe de symétrie, trouvez\(y=-\dfrac{b}{2 a}\)	\(y=-\dfrac{b}{2 a}\)
	\(y=-\dfrac{2}{2(-1)}\)
	\(y=1\)
	L'axe de symétrie est\(y=1\).
Le sommet se trouve sur la ligne\(y=1\).	\(x=-y^{2}+2 y+8\)
Laissez\(y=1\).	$.$
	\(x=9\)
	Le sommet est\((9,1)\).
Le\(x\) -intercept se produit lorsque\(y=0\).	\(x=-y^{2}+2 y+8\)
	$.$
	\(x=8\)
	Le\(x\) -intercept est\((8,0)\).
Le point\((8,0)\) se trouve à une unité en dessous de la ligne de symétrie. Le point symétrique situé à une unité au-dessus de la ligne de symétrie est\((8,2)\)	Le point symétrique est\((8,2)\).
Le\(y\) -intercept se produit lorsque\(x=0\).	\(x=-y^{2}+2 y+8\)
Substitut\(x=0\).	\(0=-y^{2}+2 y+8\)
Résoudre.	\(y^{2}-2 y-8=0\)
	\((y-4)(y+2)=0\)
	\(y=4, \quad y=-2\)
	Les\(y\) -intercepts sont\((0,4)\) et\((0,-2)\).
Reliez les points pour représenter graphiquement la parabole.	$.$

	$.$
Identifiez les constantes\(a, h, k\).	\(a=2, h=1, k=2\)
Depuis\(a=2\), la parabole s'ouvre vers la droite.
$.$
L'axe de symétrie est\(y=k\).	L'axe de symétrie est\(y=2\).
Le sommet est\((h,k)\).	Le sommet est\((1,2)\).
Trouvez le\(x\) -intercept en le remplaçant\(y=0\).	\(x=2(y-2)^{2}+1\) \(x=2(0-2)^{2}+1\) \(x=9\)
	Le\(x\) -intercept est\((9,0)\).
Trouvez le point symétrique par rapport à\((9,0)\) l'axe de symétrie.	\((9,4)\)
Trouvez les\(y\) -intercepts. Laissez\(x=0\).	\(\begin{aligned} x &=2(y-2)^{2}+1 \\ 0 &=2(y-2)^{2}+1 \\-1 &=2(y-2)^{2} \end{aligned}\)
	Un carré ne peut pas être négatif, il n'y a donc pas de véritable solution. Il n'y a donc pas\(y\) d'interception.
Tracez la parabole.	$.$

	$.$
Identifiez les constantes\(a, h, k\).	\(a=-4, h=4, k=-1\)
Depuis\(a=-4\), la parabole s'ouvre vers la gauche.
$.$
L'axe de symétrie est\(y=k\).	L'axe de symétrie est\(y=-1\).
Le sommet est\((h,k)\).	Le sommet est\((4,-1)\).
Trouvez le\(x\) -intercept en le remplaçant\(y=0\).	\(x=-4(y+1)^{2}+4\) \(x=-4(0+1)^{2}+4\) \(x=0\)
	Le\(x\) -intercept est\((0,0)\).
Trouvez le point symétrique par rapport à\((0,0)\) l'axe de symétrie.	\((0,-2)\)
Trouvez les\(y\) -intercepts.	\(x=-4(y+1)^{2}+4\)
Laissez\(x=0\).	\(\begin{aligned} 0 &=-4(y+1)^{2}+4 \\-4 &=-4(y+1)^{2} \\ 1 &=(y+1)^{2} \\ y+1 &=\pm 1 \end{aligned}\)
	\(y=-1+1 \quad y=-1-1\)
	\(y=0 \quad\quad y=-2\)
	Les\(y\) -intercepts sont\((0,0)\) et\((0,-2)\).
Tracez la parabole.	$.$

	\(x=2 y^{2}+12 y+17\)
Réécrivez la fonction\(x=a(y-k)^{2}+h\) sous forme en complétant le carré.	\(x=2\left(y^{2}+6 y\right)+17\)
	$.$
	\(x=2(y+3)^{2}-1\)
	$.$
Identifiez les constantes\(a, h, k\).	\(a=2, h=-1, k=-3\)
Depuis\(a=2\), la parabole s'ouvre vers la droite.
$.$
L'axe de symétrie est\(y=k\).	L'axe de symétrie est\(y=-3\).
Le sommet est\((h,k)\).	Le sommet est\((-1,-3)\).
Trouvez le\(x\) -intercept en le remplaçant\(y=0\).	\(x=2(y+3)^{2}-1\) \(x=2(0+3)^{2}-1\) \(x=17\)
	Le\(x\) -intercept est\((17,0)\).
Trouvez le point symétrique par rapport à\((17,0)\) l'axe de symétrie.	\((17,-6)\)
Trouvez les\(y\) -intercepts. Laissez\(x=0\).	\(\begin{aligned} x &=2(y+3)^{2}-1 \\ 0 &=2(y+3)^{2}-1 \\ 1 &=2(y+3)^{2} \\ \dfrac{1}{2} &=(y+3)^{2} \\ y+3 &=\pm \sqrt{\dfrac{1}{2}} \\ y &=-3 \pm \dfrac{\sqrt{2}}{2} \end{aligned}\)
	\(y=-3+\dfrac{\sqrt{2}}{2} \quad y=-3-\dfrac{\sqrt{2}}{2}\)
	\(y \approx-2.3 \quad y \approx-3.7\)
	Les\(y\) -intercepts sont\(\left(0,-3+\dfrac{\sqrt{2}}{2}\right),\left(0,-3-\dfrac{\sqrt{2}}{2}\right)\).
Tracez la parabole.	$.$

Laissez le côté inférieur gauche du pont être l'origine de la grille de coordonnées au point\((0,0)\). Comme la base mesure les\(20\) pieds de large, le point\((20,0)\) représente le côté inférieur droit. Le pont mesure 10 pieds de haut au point le plus élevé. Le point le plus élevé est le sommet de la parabole, donc la\(y\) coordonnée -du sommet sera\(10\). Comme le pont est symétrique, le sommet doit se situer à mi-chemin entre le point le plus à gauche et le point le plus à droite\((20,0)\).\((0,0)\) De là, nous savons que la\(x\) coordonnée du sommet sera également\(10\).	$.$
Identifiez le sommet,\((h,k)\).	\((h, k)=(10,10)\)
	\(h=10, \quad k=10\)
Remplacez les valeurs dans le formulaire standard. La valeur de\(a\) est encore inconnue. Pour trouver la valeur de,\(a\) utilisez l'un des autres points de la parabole.	\(\begin{aligned} y &=a(x-h)^{2}+k \\ y &=a(x-10)^{2}+10 \\(x, y) &=(0,0) \end{aligned}\)
Remplacez les valeurs de l'autre point dans l'équation.	\(y=a(x-10)^{2}+10\) \(0=a(0-10)^{2}+10\)
Résolvez pour\(a\).	\(\begin{aligned} 0 &=a(0-10)^{2}+10 \\-10 &=a(-10)^{2} \\-10 &=100 a \\ \dfrac{-10}{100} &=a \\ a &=-\dfrac{1}{10} \end{aligned}\)
	\(y=a(x-10)^{2}+10\)
Remplacez la valeur par\(a\) dans l'équation.	\(y=-\dfrac{1}{10}(x-10)^{2}+10\)