Skip to main content
Global

Chapitre 10 Exercices de révision

  1. Last updated
  2. Save as PDF
  • Page ID
    194296

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Exercices de révision des

    Trouver des fonctions composites et inverses

    Exercice\(\PageIndex{1}\) Find and Evaluate Composite Functions

    Dans les exercices suivants, pour chaque paire de fonctions, trouvez

    1. \((f \circ g)(x)\)
    2. \((g \circ f)(x)\)
    3. \((f \cdot g)(x)\)

    1. \(f(x)=7 x-2\)et\(g(x)=5 x+1\)

    2. \(f(x)=4 x\)et\(g(x)=x^{2}+3 x\)

    Réponse

    2.

    1. \(4 x^{2}+12 x\)
    2. \(16 x^{2}+12 x\)
    3. \(4 x^{3}+12 x^{2}\)
    Exercice\(\PageIndex{2}\) Find and Evaluate Composite Functions

    Dans les exercices suivants, évaluez la composition.

    1. Pour les fonctions\(f(x)=3 x^{2}+2\) et\(g(x)=4 x-3\), trouvez
      1. \((f \circ g)(-3)\)
      2. \((g \circ f)(-2)\)
      3. \((f \circ f)(-1)\)
    2. Pour les fonctions\(f(x)=2 x^{3}+5\) et\(g(x)=3 x^{2}-7\), trouvez
      1. \((f \circ g)(-1)\)
      2. \((g \circ f)(-2)\)
      3. \((g \circ g)(1)\)
    Réponse

    2.

    1. \(-123\)
    2. \(356\)
    3. \(41\)
    Exercice\(\PageIndex{3}\) Determine Whether a Function is One-to-One

    Dans les exercices suivants, pour chaque ensemble de paires ordonnées, déterminez si elle représente une fonction et, dans l'affirmative, si la fonction est univoque.

    1. \(\begin{array}{l}{\{(-3,-5),(-2,-4),(-1,-3),(0,-2)} , {(-1,-1),(-2,0),(-3,1) \}}\end{array}\)
    2. \(\begin{array}{l}{\{(-3,0),(-2,-2),(-1,0),(0,1)} , {(1,2),(2,1),(3,-1) \}}\end{array}\)
    3. \(\begin{array}{l}{\{(-3,3),(-2,1),(-1,-1),(0,-3)} , {(1,-5),(2,-4),(3,-2) \}}\end{array}\)
    Réponse

    2. Fonction ; pas en tête-à-tête

    Exercice\(\PageIndex{4}\) Determine Whether a Function is One-to-One

    Dans les exercices suivants, déterminez si chaque graphique est le graphe d'une fonction et, dans l'affirmative, s'il s'agit d'un graphique un-à-un.


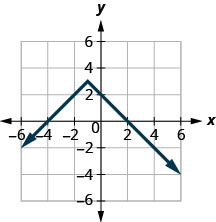
      1. Cette figure montre une ligne allant de (négatif 6, moins 2) jusqu'à (négatif 1, 3), puis vers le bas jusqu'à (6, négatif 4).
        Figure 10.E.1

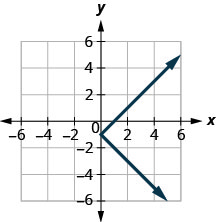
      2. Cette figure montre une ligne allant de (6, 5) vers le bas jusqu'à (0, moins 1), puis vers le bas jusqu'à (5, moins 6).
        Graphique 10.E.2

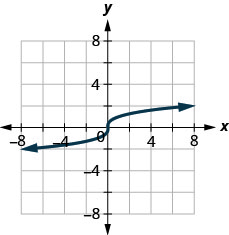
      1. Cette figure montre une ligne courbe allant de (négatif 6, moins 2) jusqu'à l'origine, puis continuant vers le haut jusqu'à (6, 2).
        Graphique 10.E.3

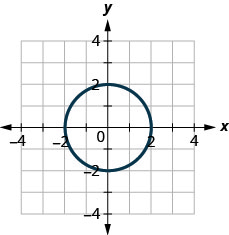
      2. Cette figure montre un cercle de rayon 2 dont le centre se trouve à l'origine.
        Graphique 10.E.4
    Réponse

    1.

    1. Fonction ; pas en tête-à-tête
    2. Pas une fonction
    Exercice\(\PageIndex{5}\) Find the Inverse of a Function

    Dans l'exercice suivant, trouvez l'inverse de la fonction. Déterminez le domaine et la plage de la fonction inverse.

    1. \(\{(-3,10),(-2,5),(-1,2),(0,1)\}\)
    Réponse

    1. Fonction inverse :\(\{(10,-3),(5,-2),(2,-1),(1,0)\}\). Domaine :\(\{1,2,5,10\}\). Gamme :\(\{-3,-2,-1,0\}\).

    Exercice\(\PageIndex{6}\) Find the Inverse of a Function

    Dans l'exercice suivant, tracez l'inverse de la fonction biunivoque illustrée.

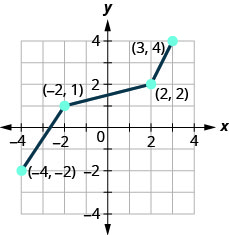
    Cette figure montre un segment de ligne allant de (négatif 4, négatif 2) à (négatif 2, 1) puis jusqu'à (2, 2) puis jusqu'à (3, 4).
    Graphique 10.E.5
    Réponse

    Résolvez vous-même

    Exercice\(\PageIndex{7}\) Find the Inverse of a Function

    Dans les exercices suivants, vérifiez que les fonctions sont des fonctions inverses.

    1. \(\begin{array}{l}{f(x)=3 x+7 \text { and }} {g(x)=\frac{x-7}{3}}\end{array}\)
    2. \(\begin{array}{l}{f(x)=2 x+9 \text { and }} {g(x)=\frac{x+9}{2}}\end{array}\)
    Réponse

    1. \(g(f(x))=x,\)\(f(g(x))=x,\)ce sont donc des inverses.

    Exercice\(\PageIndex{8}\) Find the Inverse of a Function
    1. \(f(x)=6 x-11\)
    2. \(f(x)=x^{3}+13\)
    3. \(f(x)=\frac{1}{x+5}\)
    4. \(f(x)=\sqrt[5]{x-1}\)
    Réponse

    1. \(f^{-1}(x)=\frac{x+11}{6}\)

    3. \(f^{-1}(x)=\frac{1}{x}-5\)

    Évaluer et représenter graphiquement des fonctions exponentielles

    Exercice\(\PageIndex{9}\) Graph Exponential Functions

    Dans les exercices suivants, représentez graphiquement chacune des fonctions suivantes.

    1. \(f(x)=4^{x}\)
    2. \(f(x)=\left(\frac{1}{5}\right)^{x}\)
    3. \(g(x)=(0.75)^{x}\)
    4. \(g(x)=3^{x+2}\)
    5. \(f(x)=(2.3)^{x}-3\)
    6. \(f(x)=e^{x}+5\)
    7. \(f(x)=-e^{x}\)
    Réponse

    1.

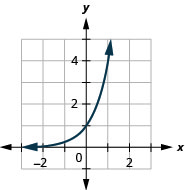
    Cette figure montre une ligne exponentielle passant par les points (moins 1, 1 sur 4), (0, 1) et (1, 4).
    Graphique 10.E.6

    3.

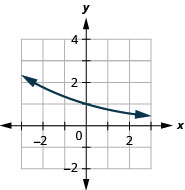
    Cette figure montre une ligne exponentielle passant par les points (moins 1, 4 sur 3), (0, 1) et (1, 3 sur 4).
    Graphique 10.E.7

    5.

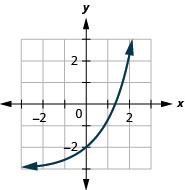
    Cette figure montre une ligne exponentielle passant par les points (moins 1, moins 59 sur 23), (0, moins 2) et (1, négatif 7 sur 10).
    Graphique 10.E.8

    7.

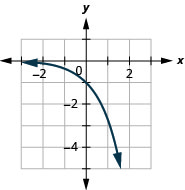
    Cette figure montre une ligne exponentielle passant par les points (moins 1, moins 1 sur e), (0, moins 1) et (1, négatif e).
    Graphique 10.E.9
    Exercice\(\PageIndex{10}\) Solve Exponential Equations

    Dans les exercices suivants, résolvez chaque équation.

    1. \(3^{5 x-6}=81\)
    2. \(2^{x^{2}}=16\)
    3. \(9^{x}=27\)
    4. \(5^{x^{2}+2 x}=\frac{1}{5}\)
    5. \(e^{4 x} \cdot e^{7}=e^{19}\)
    6. \(\frac{e^{x^{2}}}{e^{15}}=e^{2 x}\)
    Réponse

    2. \(x=-2, x=2\)

    4. \(x=-1\)

    6. \(x=-3, x=5\)

    Exercice\(\PageIndex{11}\) Use Exponential Models in Applications

    Dans les exercices suivants, résolvez.

    1. Felix a investi $\(12,000\) dans un compte d'épargne. Si le taux d'intérêt est de\(4\) %, quel sera le montant du compte en\(12\) années selon chaque méthode de composition ?
      1. trimestriel composé
      2. mensuel composé
      3. composé en continu
    2. Sayed dépose $\(20,000\) sur un compte d'investissement. Quelle sera la valeur de son investissement en\(30\) années s'il rapporte\(7\) % par an et s'il est composé de façon continue ?
    3. Un chercheur du Center for Disease Control and Prevention étudie la croissance d'une bactérie. Elle commence son expérience avec\(150\) les bactéries qui se développent à un taux de\(15\) % par heure. Elle vérifiera la présence de la bactérie toutes les\(24\) heures. Combien de bactéries trouvera-t-il en\(24\) quelques heures ?
    4. Au cours des cinq dernières années, la population des États-Unis a augmenté à un taux de\(0.7\) % par an pour atteindre environ\(318,900,000\). Si ce taux se maintient, quelle sera la population dans les années\(5\) à venir ?
    Réponse

    2. \(\$ 163,323.40\)

    4. \(330,259,000\)

    Évaluer et représenter graphiquement les fonctions logarithmiques

    Exercice\(\PageIndex{12}\) Convert Between Exponential and Logarithmic Form

    Dans les exercices suivants, passez d'une forme exponentielle à une forme logarithmique.

    1. \(5^{4}=625\)
    2. \(10^{-3}=\frac{1}{1,000}\)
    3. \(63^{\frac{1}{5}}=\sqrt[5]{63}\)
    4. \(e^{y}=16\)
    Réponse

    2. \(\log \frac{1}{1,000}=-3\)

    4. \(\ln 16=y\)

    Exercice\(\PageIndex{13}\) Convert Between Exponential and Logarithmic Form

    Dans les exercices suivants, convertissez chaque équation logarithmique en une forme exponentielle.

    1. \(7=\log _{2} 128\)
    2. \(5=\log 100,000\)
    3. \(4=\ln x\)
    Réponse

    2. \(100000=10^{5}\)

    Exercice\(\PageIndex{14}\) Evaluate Logarithmic Functions

    Dans les exercices suivants, résolvez pour\(x\).

    1. \(\log _{x} 125=3\)
    2. \(\log _{7} x=-2\)
    3. \(\log _{\frac{1}{2}} \frac{1}{16}=x\)
    Réponse

    1. \(x=5\)

    3. \(x=4\)

    Exercice\(\PageIndex{15}\) Evaluate Logarithmic Functions

    Dans les exercices suivants, déterminez la valeur exacte de chaque logarithme sans utiliser de calculatrice.

    1. \(\log _{2} 32\)
    2. \(\log _{8} 1\)
    3. \(\log _{3} \frac{1}{9}\)
    Réponse

    2. \(0\)

    Exercice\(\PageIndex{16}\) Graph Logarithmic Functions

    Dans les exercices suivants, tracez graphiquement chaque fonction logarithmique.

    1. \(y=\log _{5} x\)
    2. \(y=\log _{\frac{1}{4}} x\)
    3. \(y=\log _{0.8} x\)
    Réponse

    1.

    Cette figure montre une droite logarithmique passant par les points (1 sur 5, moins 1), (1, 0) et (5, 1).
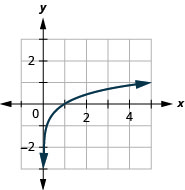
    Graphique 10.E.10

    3.

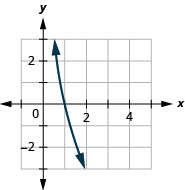
    Cette figure montre une droite logarithmique passant par les points (4 sur 5, 1), (1, 0) et (5 sur 4, moins 1).
    Figure 10.E.11
    Exercice\(\PageIndex{17}\) Solve Logarithmic Equations

    Dans les exercices suivants, résolvez chaque équation logarithmique.

    1. \(\log _{a} 36=5\)
    2. \(\ln x=-3\)
    3. \(\log _{2}(5 x-7)=3\)
    4. \(\ln e^{3 x}=24\)
    5. \(\log \left(x^{2}-21\right)=2\)
    Réponse

    2. \(x=e^{-3}\)

    4. \(x=8\)

    Exercice\(\PageIndex{18}\) Use Logarithmic Models in Applications

    Quel est le niveau de décibels d'un sifflet de train avec une intensité en\(10^{−3}\) watts par pouce carré ?

    Réponse

    \(90\)dB

    Utiliser les propriétés des logarithmes

    Exercice\(\PageIndex{19}\) Use the Properties of Logarithms

    Dans les exercices suivants, utilisez les propriétés des logarithmes pour évaluer.

      1. \(\log _{7} 1\)
      2. \(\log _{12} 12\)
      1. \(5^{\log _{5} 13}\)
      2. \(\log _{3} 3^{-9}\)
      1. \(10^{\log \sqrt{5}}\)
      2. \(\log 10^{-3}\)
      1. \(e^{\ln 8}\)
      2. \(\ln e^{5}\)
    Réponse

    2.

    1. \(13\)
    2. \(-9\)

    4.

    1. \(8\)
    2. \(5\)
    Exercice\(\PageIndex{20}\) Use the Properties of Logarithms

    Dans les exercices suivants, utilisez la propriété de produit des logarithmes pour écrire chaque logarithme sous la forme d'une somme de logarithmes. Simplifiez si possible.

    1. \(\log _{4}(64 x y)\)
    2. \(\log 10,000 m\)
    Réponse

    2. \(4+\log m\)

    Exercice\(\PageIndex{21}\) Use the Properties of Logarithms

    Dans les exercices suivants, utilisez la propriété quotient des logarithmes pour écrire chaque logarithme sous la forme d'une somme de logarithmes. Simplifiez, si possible.

    1. \(\log _{7} \frac{49}{y}\)
    2. \(\ln \frac{e^{5}}{2}\)
    Réponse

    2. \(5-\ln 2\)

    Exercice\(\PageIndex{22}\) Use the Properties of Logarithms

    Dans les exercices suivants, utilisez la propriété Power des logarithmes pour développer chaque logarithme. Simplifiez, si possible.

    1. \(\log x^{-9}\)
    2. \(\log _{4} \sqrt[7]{z}\)
    Réponse

    2. \(\frac{1}{7} \log _{4} z\)

    Exercice\(\PageIndex{23}\) Use the Properties of Logarithms

    Dans les exercices suivants, utilisez les propriétés des logarithmes pour écrire chaque logarithme sous la forme d'une somme de logarithmes. Simplifiez si possible.

    1. \(\log _{3}\left(\sqrt{4} x^{7} y^{8}\right)\)
    2. \(\log _{5} \frac{8 a^{2} b^{6} c}{d^{3}}\)
    3. \(\ln \frac{\sqrt{3 x^{2}-y^{2}}}{z^{4}}\)
    4. \(\log _{6} \sqrt[3]{\frac{7 x^{2}}{6 y^{3} z^{5}}}\)
    Réponse

    2. \(\begin{array}{l}{\log _{5} 8+2 \log _{5} a+6 \log _{5} b} {+\log _{5} c-3 \log _{5} d}\end{array}\)

    4. \(\begin{array}{l}{\frac{1}{3}\left(\log _{6} 7+2 \log _{6} x-1-3 \log _{6} y\right.} {-5 \log _{6} z )}\end{array}\)

    Exercice\(\PageIndex{24}\) Use the Properties of Logarithms

    Dans les exercices suivants, utilisez les propriétés des logarithmes pour condenser le logarithme. Simplifiez si possible.

    1. \(\log _{2} 56-\log _{2} 7\)
    2. \(3 \log _{3} x+7 \log _{3} y\)
    3. \(\log _{5}\left(x^{2}-16\right)-2 \log _{5}(x+4)\)
    4. \(\frac{1}{4} \log y-2 \log (y-3)\)
    Réponse

    2. \(\log _{3} x^{3} y^{7}\)

    4. \(\log \frac{\sqrt[4]{y}}{(y-3)^{2}}\)

    Exercice\(\PageIndex{25}\) Use the Change-of-Base Formula

    Dans les exercices suivants, en arrondissant à trois décimales, approximativement chaque logarithme.

    1. \(\log _{5} 97\)
    2. \(\log _{\sqrt{3}} 16\)
    Réponse

    2. \(5.047\)

    Résoudre des équations exponentielles et logarithmiques

    Exercice\(\PageIndex{26}\) Solve Logarithmic Equations Using the Properties of Logarithms

    Dans les exercices suivants, résolvez pour\(x\).

    1. \(3 \log _{5} x=\log _{5} 216\)
    2. \(\log _{2} x+\log _{2}(x-2)=3\)
    3. \(\log (x-1)-\log (3 x+5)=-\log x\)
    4. \(\log _{4}(x-2)+\log _{4}(x+5)=\log _{4} 8\)
    5. \(\ln (3 x-2)=\ln (x+4)+\ln 2\)
    Réponse

    2. \(x=4\)

    4. \(x=3\)

    Exercice\(\PageIndex{27}\) Solve Exponential Equations Using Logarithms

    Dans les exercices suivants, résolvez chaque équation exponentielle. Trouvez la réponse exacte, puis approchez-la à trois décimales près.

    1. \(2^{x}=101\)
    2. \(e^{x}=23\)
    3. \(\left(\frac{1}{3}\right)^{x}=7\)
    4. \(7 e^{x+3}=28\)
    5. \(e^{x-4}+8=23\)
    Réponse

    1. \(x=\frac{\log 101}{\log 2} \approx 6.658\)

    3. \(x=\frac{\log 7}{\log \frac{1}{3}} \approx-1.771\)

    5. \(x=\ln 15+4 \approx 6.708\)

    Exercice\(\PageIndex{28}\) Use Exponential Models in Applications
    1. Jérôme investit $\(18,000\) à l'âge\(17\). Il espère que les investissements vaudront $\(30,000\) à son tour\(26\). Si l'intérêt augmente continuellement, de quel taux de croissance aura-t-il besoin approximativement pour atteindre son objectif ? Est-ce une attente raisonnable ?
    2. Elise investit $\(4500\) dans un compte qui compose les intérêts chaque mois et gagne\(6\) %. Combien de temps faudra-t-il pour que son argent double ?
    3. Les chercheurs ont enregistré qu'une certaine population de bactéries augmentait de\(100\) à\(300\) en\(8\) quelques heures. À ce rythme de croissance, combien de bactéries y aura-t-il en\(24\) quelques heures ?
    4. Les populations de souris peuvent doubler en\(8\) quelques mois\(\left(A=2 A_{0}\right)\). Combien de temps faudra-t-il pour que la population de souris triple ?
    5. La demi-vie de l'iode radioactif est de\(60\) quelques jours. Quelle quantité d'un échantillon de\(50\) mg restera-t-il en\(40\) quelques jours ?
    Réponse

    2. \(11.6\)ans

    4. \(12.7\)mois

    Test d'entraînement

    Exercice\(\PageIndex{29}\)
    1. Pour les fonctions\(g(x)=8x−3\),\(f(x)=6x+1\) et trouvez
      1. \((f \circ g)(x)\)
      2. \((g \circ f)(x)\)
      3. \((f \cdot g)(x)\)
    2. Déterminez si l'ensemble de paires ordonnées suivant représente une fonction et, dans l'affirmative, s'agit-il d'une fonction univoque. \(\{(-2,2),(-1,-3),(0,1),(1,-2),(2,-3)\}\)
    3. Déterminez si chaque graphique est le graphe d'une fonction et, dans l'affirmative, s'il s'agit d'un graphique à un.

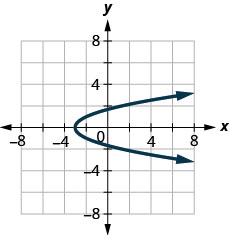
      1. Cette figure montre une parabole s'ouvrant vers la droite avec un sommet (négatif 3, 0).
        Figure 10.E.12

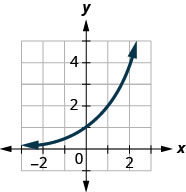
      2. Cette figure montre une ligne exponentielle passant par les points (moins 1, 1 sur 2), (0, 1) et (1, 2).
        Figure 10.E.13
    4. Tracez, sur le même système de coordonnées, l'inverse de la fonction biunivoque affichée.
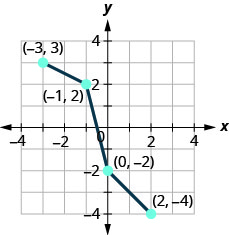
    Cette figure montre un segment de droite passant du point (négatif 3, 3) à (négatif 1, 2) à (0, négatif 2) à (2, négatif 4).
    Graphique 10.E.14

    5. Trouvez l'inverse de la fonction\(f(x)=x^{5}−9\).

    6. Tracez la fonction\(g(x)=2^{x-3}\).

    7. Résolvez l'équation\(2^{2 x-4}=64\).

    8. Résolvez l'équation\(\frac{e^{x^{2}}}{e^{4}}=e^{3 x}\).

    9. Megan a investi $\(21,000\) dans un compte d'épargne. Si le taux d'intérêt est de\(5\) %, quel sera le montant du compte en\(8\) années selon chaque méthode de composition ?

    1. trimestriel composé
    2. mensuel composé
    3. composé en continu

    10. Convertissez l'équation de la forme exponentielle à la forme logarithmique :\(10^{-2}=\frac{1}{100}\).

    11. Convertissez l'équation de l'équation logarithmique à la forme exponentielle :\(3=\log _{7} 343\).

    12. Résolvez pour\(x\) :\(\log _{5} x=-3\)

    13. Journal d'évaluation\(_{11} 1\).

    14. Évaluer\(\log _{4} \frac{1}{64}\).

    15. Tracez la fonction\(y=\log _{3} x\).

    16. Résolvez pour\(x\) :\(\log \left(x^{2}-39\right)=1\)

    17. Quel est le niveau de décibels d'un petit ventilateur d'une intensité en\(10^{−8}\) watts par pouce carré ?

    18. Évaluez chacun.

    1. \(6^{\log _{6} 17}\)
    2. \(\log _{9} 9^{-3}\)
    Réponse

    1.

    1. \(48 x-17\)
    2. \(48 x+5\)
    3. \(48 x^{2}-10 x-3\)

    3.

    1. Pas une fonction
    2. Fonction un à un

    5. \(f^{-1}(x)=\sqrt[5]{x+9}\)

    7. \(x=5\)

    9.

    1. $\(31,250.74\)
    2. $\(31,302.29\)
    3. $\(31,328.32\)

    11. \(343=7^{3}\)

    13. \(0\)

    15.

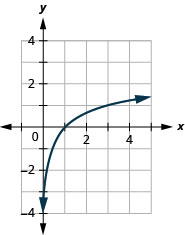
    Cette figure montre une droite logarithmique passant par (1 sur 3, 1), (1, 0) et (3, 1).
    Figure 10.E.15

    17. \(40\)dB

    Exercice\(\PageIndex{30}\)

    Dans les exercices suivants, utilisez les propriétés des logarithmes pour écrire chaque expression sous la forme d'une somme de logarithmes, en simplifiant si possible.

    1. \(\log _{5} 25 a b\)
    2. \(\ln \frac{e^{12}}{8}\)
    3. \(\log _{2} \sqrt[4]{\frac{5 x^{3}}{16 y^{2} z^{7}}}\)
    Réponse

    1. \(2+\log _{5} a+\log _{5} b\)

    3. \(\begin{array}{l}{\frac{1}{4}\left(\log _{2} 5+3 \log _{2} x-4-2 \log _{2} y\right.} {-7 \log _{2} z )}\end{array}\)

    Exercice\(\PageIndex{31}\)

    Dans les exercices suivants, utilisez les propriétés des logarithmes pour condenser le logarithme, en simplifiant si possible.

    1. \(5 \log _{4} x+3 \log _{4} y\)
    2. \(\frac{1}{6} \log x-3 \log (x+5)\)
    3. En arrondissant à trois décimales, valeur approximative\(\log _{4} 73\).
    4. Résolvez pour\(x\) :\(\log _{7}(x+2)+\log _{7}(x-3)=\log _{7} 24\)
    Réponse

    2. \(\log \frac{\sqrt[6]{x}}{(x+5)^{3}}\)

    4. \(x=6\)

    Exercice\(\PageIndex{32}\)

    Dans les exercices suivants, résolvez chaque équation exponentielle. Trouvez la réponse exacte, puis approchez-la à trois décimales près.

    1. \(\left(\frac{1}{5}\right)^{x}=9\)
    2. \(5 e^{x-4}=40\)
    3. Jacob investit $\(14,000\) dans un compte qui compose les intérêts trimestriels et gagne\(4\) %. Combien de temps faudra-t-il pour que son argent double ?
    4. Les chercheurs ont enregistré qu'une certaine population de bactéries augmentait de\(500\) à\(700\) en\(5\) quelques heures. À ce rythme de croissance, combien de bactéries y aura-t-il en\(20\) quelques heures ?
    5. Une certaine population de coléoptères peut doubler en\(3\) quelques mois\(\left(A=2 A_{0}\right)\). Combien de temps faudra-t-il pour que cette population de coléoptères triple ?
    Réponse

    2. \(x=\ln 8+4 \approx 6.079\)

    4. \(1,921\)bactéries