9.3 : Résolvez des équations quadratiques en complétant le carré
- Page ID
- 194375
À la fin de cette section, vous serez en mesure de :
- Compléter le carré d'une expression binomiale
- Résolvez les équations quadratiques de la forme\(x^{2}+bx+c=0\) en complétant le carré
- Résolvez les équations quadratiques de la forme\(ax^{2}+bx+c=0\) en complétant le carré
Avant de commencer, répondez à ce questionnaire de préparation.
- Agrandir :\((x+9)^{2}\).
Si vous avez oublié ce problème, consultez l'exemple 5.32. - Facteur\(y^{2}-14 y+49\).
Si vous avez oublié ce problème, consultez l'exemple 6.9. - Facteur\(5 n^{2}+40 n+80\).
Si vous avez oublié ce problème, consultez l'exemple 6.14.
Jusqu'à présent, nous avons résolu des équations quadratiques en factorisant et en utilisant la propriété Square Root. Dans cette section, nous allons résoudre des équations quadratiques par un processus appelé complétion du carré, qui sera important pour nos travaux ultérieurs sur les coniques.
Compléter le carré d'une expression binomiale
Dans la dernière section, nous avons pu utiliser la propriété Square Root pour résoudre l'équation,\((y-7)^{2}=12\) car le côté gauche était un carré parfait.
\(\begin{aligned}(y-7)^{2} &=12 \\ y-7 &=\pm \sqrt{12} \\ y-7 &=\pm 2 \sqrt{3} \\ y &=7 \pm 2 \sqrt{3} \end{aligned}\)
Nous avons également résolu une équation dans laquelle le côté gauche était un trinôme carré parfait, mais nous avons dû la réécrire sous sa forme\((x−k)^{2}\) afin d'utiliser la propriété Square Root.
\(\begin{aligned} x^{2}-10 x+25 &=18 \\(x-5)^{2} &=18 \end{aligned}\)
Que se passe-t-il si la variable ne fait pas partie d'un carré parfait ? Pouvons-nous utiliser l'algèbre pour créer un carré parfait ?
Examinons deux exemples pour nous aider à identifier les modèles.
\(\begin{array}{cc}{(x+9)^{2}} & {(y-7)^{2}} \\ {(x+9 )(x+9)} & {(y-7)(y-7)} \\ {x^{2}+9 x+9 x+81} & {y^{2}-7 y-7 y+49} \\ {x^{2}+18 x+81} & {y^{2}-14 y+49}\end{array}\)
Nous reprenons les modèles ici à titre de référence.
Si\(a\) et\(b\) sont des nombres réels,
Nous pouvons utiliser ce modèle pour « créer » un carré parfait.
Nous allons commencer par l'expression\(x^{2}+6 x\). Comme il y a un signe plus entre les deux termes, nous utiliserons le\((a+b)^{2}\) modèle,\(a^{2}+2 a b+b^{2}=(a+b)^{2}\).
Nous devons finalement trouver le dernier terme de ce trinôme qui en fera un trinôme carré parfait. Pour ce faire, nous devrons trouver\(b\). Mais nous commençons par déterminer\(a\). Notez que le premier terme de\(x^{2}+6x\) est un carré,\(x^{2}\). Cela nous indique que\(a=x\).
Quel nombre\(b\), lorsqu'il est multiplié par un\(2x\) donne\(6x\) ? Il faudrait que ce soit le cas\(3\), ce qui est le cas\(\frac{1}{2}(6)\). Donc\(b=3\).
Maintenant, pour compléter le trinôme carré parfait, nous allons trouver le dernier terme en mettant au carré\(b\), c'est-à-dire\(3^{2}=9\).
Nous pouvons maintenant prendre en compte.
Nous avons donc constaté que l'ajout\(9\) de\(x^{2}+6 x\) « complète le carré », et nous l'écrivons ainsi\((x+3)^{2}\).
- Identifiez\(b\), le coefficient de\(x\).
- Trouvez\(\left(\frac{1}{2} b\right)^{2}\) le numéro pour compléter le carré.
- Ajoutez le\(\left(\frac{1}{2} b\right)^{2}\) à\(x^{2}+bx\).
- Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré.
Complétez le carré pour obtenir un trinôme carré parfait. Écrivez ensuite le résultat sous la forme d'un carré binomial.
- \(x^{2}-26 x\)
- \(y^{2}-9 y\)
- \(n^{2}+\frac{1}{2} n\)
Solution :
un.
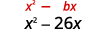 |
|
| Le coefficient de\(x\) est de -26. | |
|
Trouvez\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-26)\right)^{2}\) |
|
| Ajoutez\(169\) au binôme pour compléter le carré. |
\(x^{2}-26 x+169\) |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. |
\((x-13)^{2}\) |
b.
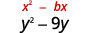 |
|
| Le coefficient de\(y\) est\(-9\). | |
|
Trouvez\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot(-9)\right)^{2}\) |
|
| Ajoutez\(\frac{81}{4}\) au binôme pour compléter le carré. |
\(y^{2}-9 y+\frac{81}{4}\) |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. |
\(\left(y-\frac{9}{2}\right)^{2}\) |
c.
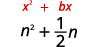 |
|
| Le coefficient de\(n\) est\(\frac{1}{2}\). | |
|
Trouvez\(\left(\frac{1}{2} b\right)^{2}\). \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)^{2}\) |
|
| Ajoutez\(\frac{1}{16}\) au binôme pour compléter le carré. | \(n^{2}+\frac{1}{2} n+\frac{1}{16}\) |
| Réécrivez sous forme de carré binomial. | \(\left(n+\frac{1}{4}\right)^{2}\) |
Complétez le carré pour obtenir un trinôme carré parfait. Écrivez ensuite le résultat sous la forme d'un carré binomial.
- \(a^{2}-20 a\)
- \(m^{2}-5 m\)
- \(p^{2}+\frac{1}{4} p\)
- Réponse
-
- \((a-10)^{2}\)
- \(\left(b-\frac{5}{2}\right)^{2}\)
- \(\left(p+\frac{1}{8}\right)^{2}\)
Complétez le carré pour obtenir un trinôme carré parfait. Écrivez ensuite le résultat sous la forme d'un carré binomial.
- \(b^{2}-4 b\)
- \(n^{2}+13 n\)
- \(q^{2}-\frac{2}{3} q\)
- Réponse
-
- \((b-2)^{2}\)
- \(\left(n+\frac{13}{2}\right)^{2}\)
- \(\left(q-\frac{1}{3}\right)^{2}\)
Résolvez les équations quadratiques de la forme\(x^{2}+bx+c=0\) en complétant le carré
Lorsque nous résolvons des équations, nous devons toujours faire la même chose des deux côtés de l'équation. Cela est vrai, bien sûr, lorsque nous résolvons une équation quadratique en complétant également le carré. Lorsque nous ajoutons un terme d'un côté de l'équation pour créer un trinôme carré parfait, nous devons également ajouter le même terme de l'autre côté de l'équation.
Par exemple, si nous commençons par l'équation\(x^{2}+6x=40\) et que nous voulons compléter le carré de gauche, nous ajouterons 9 des deux côtés de l'équation.
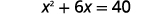 |
|
 |
|
 |
|
| Ajoutez\(9\) des deux côtés pour compléter le carré. | 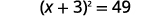 |
L'équation est maintenant sous la forme à résoudre à l'aide de la propriété Square Root ! Compléter le carré est un moyen de transformer une équation dans la forme dont nous avons besoin pour pouvoir utiliser la propriété Square Root.
Résolvez en complétant le carré :\(x^{2}+8x=48\).
Solution :
| Étape 1 : Isolez les termes variables d'un côté et les termes constants de l'autre. | Toutes les variables se trouvent sur la gauche de cette équation. | \(\begin{array}{l}{\color{red}{x^{2}+b x\quad\:\:\: c }} \\ {x^{2}+8 x=48}\end{array}\) |
| Étape 2 : Trouvez\(\left(\frac{1}{2} \cdot b\right)^{2}\) le numéro pour compléter le carré. Ajoutez-le aux deux côtés de l'équation. |
Prenez la moitié\(8\) et mettez-la au carré. \(4^{2}=16\) Ajoutez\(16\) les deux côtés de l'équation. |
\(x^{2}+8 x+\frac{}{\color{red}{\left(\frac{1}{2} \cdot 8\right)^{2}}}\color{black}{=}48 \) \(x^{2}+8 x\color{red}{+16}\color{black}{=}48\color{red}{+16}\) |
| Étape 3 : Facteur le trinôme carré parfait comme un carré binomial. |
\(x^{2}+8 x+16=(x+4)^{2}\) Ajoutez les termes sur la droite. |
\((x+4)^{2}=64\) |
| Étape 4 : Utilisez la propriété Square Root. | \(x+4=\pm \sqrt{64}\) | |
| Étape 5 : Simplifier le radical puis résoudre les deux équations résultantes. |
\(x+4=\pm 8\) \(\begin{aligned} x+4 &=8 \quad x+4=-8 \\ x &=4 \quad\quad\:\:\: x=-12 \end{aligned}\) |
|
| Étape 6 : Vérifiez les solutions. | Mettez chaque réponse dans l'équation d'origine à vérifier. Remplacer\(x=4\) et\(x=-12\). |
\(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{4}\color{black}{)}^{2}+8(\color{red}{4}\color{black}{)} \stackrel{?}{=} 48} \\ {16+32\stackrel{?}{=}48} \\ {48=48}\end{array}\) \(\begin{array}{r}{x^{2}+8 x=48} \\ {(\color{red}{-12}\color{black}{)}^{2}+8(\color{red}{-12}\color{black}{)}\stackrel{?}{=} 48} \\ {144-96 \stackrel{?}{=} 48} \\ {48=48}\end{array}\) |
Résolvez en complétant le carré :\(x^{2}+4 x=5\).
- Réponse
-
\(x=-5, x=-1\)
Résolvez en complétant le carré :\(y^{2}−10y=−9\).
- Réponse
-
\(y=1, y=9\)
Les étapes pour résoudre une équation quadratique en complétant le carré sont répertoriées ici.
Résolvez une équation quadratique de la forme\(x^{2}+bx+c=0\) en complétant le carré
- Isolez les termes variables d'un côté et les termes constants de l'autre.
- Trouvez\(\left(\frac{1}{2} \cdot b\right)^{2}\) le numéro nécessaire pour compléter le carré. Ajoutez-le aux deux côtés de l'équation.
- Facturez le trinôme carré parfait en l'écrivant sous forme de binôme au carré à gauche et simplifiez en ajoutant les termes à droite
- Utilisez la propriété Square Root.
- Simplifiez le radical, puis résolvez les deux équations résultantes.
- Vérifiez les solutions.
Lorsque nous résolvons une équation en complétant le carré, les réponses ne seront pas toujours des nombres entiers.
Résolvez en complétant le carré :\(x^{2}+4 x=-21\).
Solution :
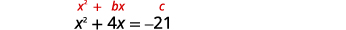 |
|
|
Les termes variables se trouvent sur le côté gauche. Prenez la moitié\(4\) et mettez-la au carré. |
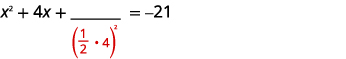 |
| \(\left(\frac{1}{2}(4)\right)^{2}=4\) | |
| Ajouter\(4\) des deux côtés. |  |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 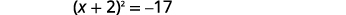 |
| Utilisez la propriété Square Root. | 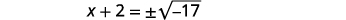 |
| Simplifier l'utilisation de nombres complexes | 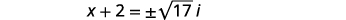 |
| Soustrayez\(2\) de chaque côté. | 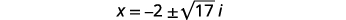 |
| Réécrivez pour afficher deux solutions. | 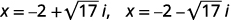 |
| Nous vous laissons le chèque. |
Résolvez en complétant le carré :\(y^{2}-10 y=-35\).
- Réponse
-
\(y=5+\sqrt{15} i, y=5-\sqrt{15 i}\)
Résolvez en complétant le carré :\(z^{2}+8 z=-19\).
- Réponse
-
\(z=-4+\sqrt{3} i, z=-4-\sqrt{3} i\)
Dans l'exemple précédent, nos solutions étaient des nombres complexes. Dans l'exemple suivant, les solutions seront des nombres irrationnels.
Résolvez en complétant le carré :\(y^{2}-18 y=-6\).
Solution :
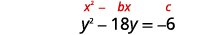 |
|
| Les termes variables se trouvent sur le côté gauche. Prenez la moitié\(-18\) et mettez-la au carré. | |
| \(\left(\frac{1}{2}(-18)\right)^{2}=81\) | 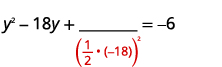 |
| Ajouter\(81\) des deux côtés. | 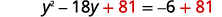 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 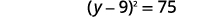 |
| Utilisez la propriété Square Root. | 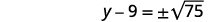 |
| Simplifiez le radical. | 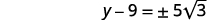 |
| Résolvez pour\(y\). |  |
|
Vérifiez. 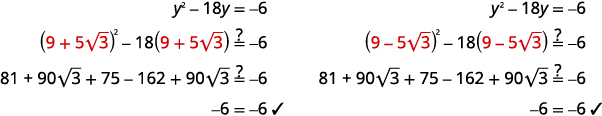
|
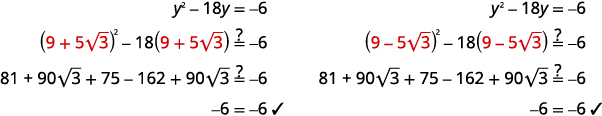 |
Une autre façon de vérifier cela serait d'utiliser une calculatrice. \(y^{2}−18y\)Évaluez les deux solutions. La réponse devrait être\(−6\).
Résolvez en complétant le carré :\(x^{2}-16 x=-16\).
- Réponse
-
\(x=8+4 \sqrt{3}, x=8-4 \sqrt{3}\)
Résolvez en complétant le carré :\(y^{2}+8 y=11\).
- Réponse
-
\(y=-4+3 \sqrt{3}, y=-4-3 \sqrt{3}\)
Nous allons commencer l'exemple suivant en isolant les termes variables sur le côté gauche de l'équation.
Résolvez en complétant le carré :\(x^{2}+10 x+4=15\).
Solution :
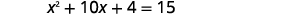 |
|
| Isolez les termes variables sur le côté gauche. Soustrayez\(4\) pour obtenir les termes constants sur le côté droit. | 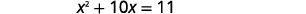 |
| Prenez la moitié\(10\) et mettez-la au carré. | |
| \(\left(\frac{1}{2}(10)\right)^{2}=25\) | 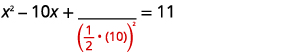 |
| Ajouter\(25\) des deux côtés. | 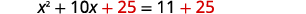 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 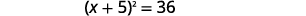 |
| Utilisez la propriété Square Root. | 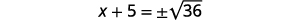 |
| Simplifiez le radical. | 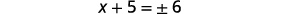 |
| Résolvez pour\(x\). | 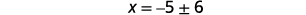 |
| Réécrivez pour afficher deux solutions. | 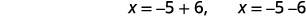 |
| Résolvez les équations. | 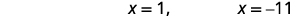 |
|
Vérifiez : 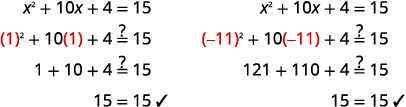
|
Résolvez en complétant le carré :\(a^{2}+4 a+9=30\).
- Réponse
-
\(a=-7, a=3\)
Résolvez en complétant le carré :\(b^{2}+8 b-4=16\).
- Réponse
-
\(b=-10, b=2\)
Pour résoudre l'équation suivante, nous devons d'abord collecter tous les termes variables sur le côté gauche de l'équation. Ensuite, nous procédons comme nous l'avons fait dans les exemples précédents.
Résolvez en complétant le carré :\(n^{2}=3 n+11\).
Solution :
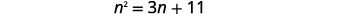 |
|
| Soustrayez\(3n\) pour obtenir les termes variables sur le côté gauche. |  |
| Prenez la moitié\(-3\) et mettez-la au carré. | |
| \(\left(\frac{1}{2}(-3)\right)^{2}=\frac{9}{4}\) | 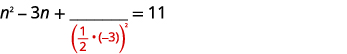 |
| Ajouter\(\frac{9}{4}\) des deux côtés. | 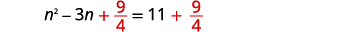 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 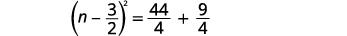 |
| Ajoutez les fractions sur le côté droit. | 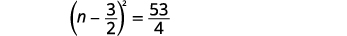 |
| Utilisez la propriété Square Root. | 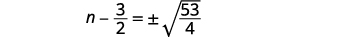 |
| Simplifiez le radical. | 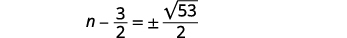 |
| Résolvez pour\(n\). | 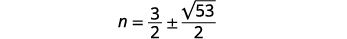 |
| Réécrivez pour afficher deux solutions. | 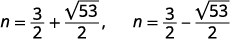 |
|
Vérifiez : Nous vous laissons le chèque ! |
Résolvez en complétant le carré :\(p^{2}=5 p+9\).
- Réponse
-
\(p=\frac{5}{2}+\frac{\sqrt{61}}{2}, p=\frac{5}{2}-\frac{\sqrt{61}}{2}\)
Résolvez en complétant le carré :\(q^{2}=7 q-3\).
- Réponse
-
\(q=\frac{7}{2}+\frac{\sqrt{37}}{2}, q=\frac{7}{2}-\frac{\sqrt{37}}{2}\)
Notez que le côté gauche de l'équation suivante est sous forme factorielle. Mais le côté droit n'est pas zéro. Nous ne pouvons donc pas utiliser la propriété Zero Product car elle indique « Si\(a⋅b=0\), alors\(a=0\) ou »\(b=0\). Au lieu de cela, nous multiplions les facteurs, puis nous mettons l'équation sous forme standard pour la résoudre en complétant le carré.
Résolvez en complétant le carré :\((x-3)(x+5)=9\).
Solution :
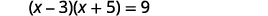 |
|
| Nous multiplions les binômes sur la gauche. | 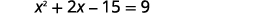 |
| Ajoutez\(15\) pour isoler les termes constants sur la droite. | 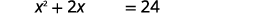 |
| Prenez la moitié\(2\) et mettez-la au carré. | |
| \(\left(\frac{1}{2} \cdot(2)\right)^{2}=1\) | 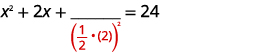 |
| Ajouter\(1\) des deux côtés. | 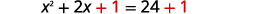 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 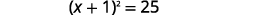 |
| Utilisez la propriété Square Root. | 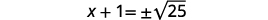 |
| Résolvez pour\(x\). | 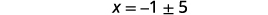 |
| Réécrivez pour afficher deux solutions. | 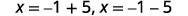 |
| Simplifiez. | 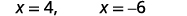 |
|
Vérifiez : Nous vous laissons le chèque ! |
Résolvez en complétant le carré :\((c-2)(c+8)=11\).
- Réponse
-
\(c=-9, c=3\)
Résolvez en complétant le carré :\((d-7)(d+3)=56\).
- Réponse
-
\(d=11, d=-7\)
Résolvez les équations quadratiques de la forme\(ax^{2}+bx+c=0\) en complétant le carré
Le processus de complétion du carré fonctionne mieux lorsque le coefficient de\(x^{2}\) est\(1\), de sorte que le côté gauche de l'équation est de la forme\(x^{2}+bx+c\). Si le\(x^{2}\) terme a un coefficient différent de\(1\), nous prenons quelques mesures préliminaires pour que le coefficient soit égal à\(1\).
Parfois, le coefficient peut être pris en compte à partir des trois termes du trinôme. Telle sera notre stratégie dans l'exemple suivant.
Résolvez en complétant le carré :\(3 x^{2}-12 x-15=0\).
Solution :
Pour compléter le carré, il faut que le coefficient\(x^{2}\) de soit un. Si nous prenons le coefficient de\(x^{2}\) comme facteur commun, nous pouvons continuer à résoudre l'équation en complétant le carré.
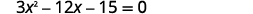 |
|
| Déterminez le plus grand facteur commun. | 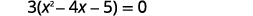 |
| Divisez les deux côtés par\(3\) pour isoler le trinôme avec un coefficient\(1\). | 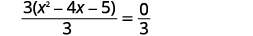 |
| Simplifiez. | 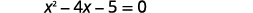 |
| Ajoutez\(5\) pour obtenir les termes constants sur le côté droit. | 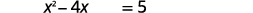 |
| Prenez la moitié\(4\) et mettez-la au carré. | |
| \(\left(\frac{1}{2}(-4)\right)^{2}=4\) | 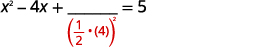 |
| Ajouter\(4\) des deux côtés. | 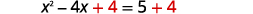 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 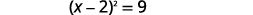 |
| Utilisez la propriété Square Root. | 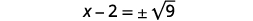 |
| Résolvez pour\(x\). | 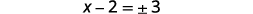 |
| Réécrivez pour afficher deux solutions. | 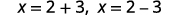 |
| Simplifiez. |  |
|
Vérifiez : 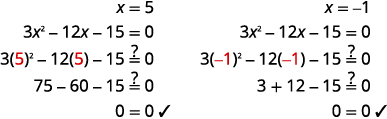
|
Résolvez en complétant le carré :\(2 m^{2}+16 m+14=0\).
- Réponse
-
\(m=-7, m=-1\)
Résolvez en complétant le carré :\(4 n^{2}-24 n-56=8\).
- Réponse
-
\(n=-2, n=8\)
Pour compléter le carré, le coefficient du\(x^{2}\) doit être\(1\). Lorsque le coefficient principal n'est pas un facteur de tous les termes, nous diviserons les deux côtés de l'équation par le coefficient principal ! Cela nous donnera une fraction pour le deuxième coefficient. Nous avons déjà vu comment compléter le carré avec des fractions dans cette section.
Résolvez en complétant le carré :\(2 x^{2}-3 x=20\).
Solution :
Pour compléter le carré, nous avons besoin que le coefficient\(x^{2}\) de soit un. Nous allons diviser les deux côtés de l'équation par le coefficient de\(x^{2}\). Ensuite, nous pouvons continuer à résoudre l'équation en complétant le carré.
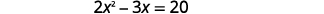 |
|
| Divisez les deux côtés par\(2\) pour obtenir le coefficient de\(x^{2}\)\(1\). | 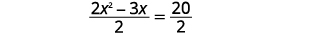 |
| Simplifiez. | 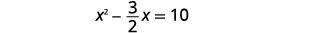 |
| Prenez la moitié\(-\frac{3}{2}\) et mettez-la au carré. | |
| \(\left(\frac{1}{2}\left(-\frac{3}{2}\right)\right)^{2}=\frac{9}{16}\) | 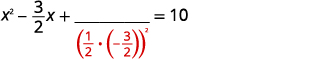 |
| Ajouter\(\frac{9}{16}\) des deux côtés. | 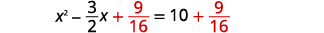 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 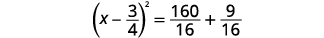 |
| Ajoutez les fractions sur le côté droit. | 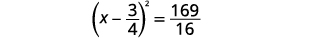 |
| Utilisez la propriété Square Root. | 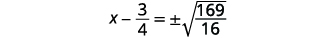 |
| Simplifiez le radical. | 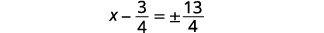 |
| Résolvez pour\(x\). | 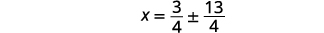 |
| Réécrivez pour afficher deux solutions. | 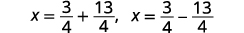 |
| Simplifiez. | 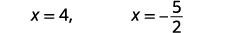 |
|
Vérifiez : Nous vous laissons le chèque ! |
Résolvez en complétant le carré :\(3 r^{2}-2 r=21\).
- Réponse
-
\(r=-\frac{7}{3}, r=3\)
Résolvez en complétant le carré :\(4 t^{2}+2 t=20\).
- Réponse
-
\(t=-\frac{5}{2}, t=2\)
Maintenant que nous avons vu que le coefficient de\(x^{2}\) doit être\(1\) pour que nous puissions compléter le carré, nous mettons à jour notre procédure de résolution d'une équation quadratique en complétant le carré pour inclure les équations de la forme\(a x^{2}+b x+c=0\).
- Divisez par aa pour obtenir le coefficient du\(x^{2}\) terme\(1\).
- Isolez les termes variables d'un côté et les termes constants de l'autre.
- Trouvez\(\left(\frac{1}{2} \cdot b\right)^{2}\) le numéro nécessaire pour compléter le carré. Ajoutez-le aux deux côtés de l'équation.
- Facturez le trinôme carré parfait en l'écrivant sous forme de binôme au carré à gauche et simplifiez en ajoutant les termes à droite
- Utilisez la propriété Square Root.
- Simplifiez le radical, puis résolvez les deux équations résultantes.
- Vérifiez les solutions.
Résolvez en complétant le carré :\(3 x^{2}+2 x=4\).
Solution :
Encore une fois, notre première étape consistera à établir le coefficient de\(x^{2}\) un. En divisant les deux côtés de l'équation par le coefficient de\(x^{2}\), nous pouvons ensuite continuer à résoudre l'équation en complétant le carré.
 |
|
| Divisez les deux côtés par\(3\) pour obtenir un coefficient\(x^{2}\) égal\(1\). | 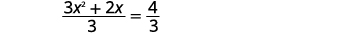 |
| Simplifiez. |  |
| Prenez la moitié\(\frac{2}{3}\) et mettez-la au carré. | |
| \(\left(\frac{1}{2} \cdot \frac{2}{3}\right)^{2}=\frac{1}{9}\) | 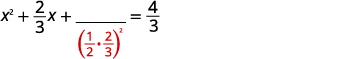 |
| Ajouter\(\frac{1}{9}\) des deux côtés. | 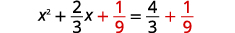 |
| Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme carré. | 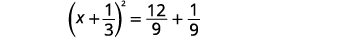 |
| Utilisez la propriété Square Root. | 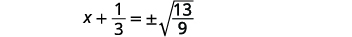 |
| Simplifiez le radical. | 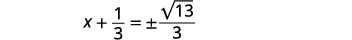 |
| Résolvez pour\(x\). | 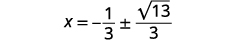 |
| Réécrivez pour afficher deux solutions. | 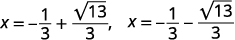 |
|
Vérifiez : Nous vous laissons le chèque ! |
Résolvez en complétant le carré :\(4 x^{2}+3 x=2\).
- Réponse
-
\(x=-\frac{3}{8}+\frac{\sqrt{41}}{8}, x=-\frac{3}{8}-\frac{\sqrt{41}}{8}\)
Résolvez en complétant le carré :\(3 y^{2}-10 y=-5\).
- Réponse
-
\(y=\frac{5}{3}+\frac{\sqrt{10}}{3}, y=\frac{5}{3}-\frac{\sqrt{10}}{3}\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires pour compléter le carré.
Concepts clés
- Schéma de carrés\(a\) binomiaux
Si et\(b\) sont des nombres réels,
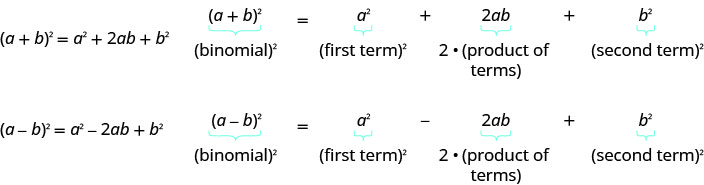
- Comment compléter un carré
- Identifiez\(b\), le coefficient de\(x\).
- Trouvez\(\left(\frac{1}{2} b\right)^{2}\) le numéro pour compléter le carré.
- Ajoutez le\(\left(\frac{1}{2} b\right)^{2}\) à\(x^{2}+bx\)
- Réécrivez le trinôme sous forme de carré binomial
- Comment résoudre une équation quadratique de la forme \(a x^{2}+b x+c=0\)en complétant le carré.
- Divisez par\(a\) pour obtenir le coefficient du\(x^{2}\) terme\(1\).
- Isolez les termes variables d'un côté et les termes constants de l'autre.
- Trouvez\(\left(\frac{1}{2} \cdot b\right)^{2}\) le numéro nécessaire pour compléter le carré. Ajoutez-le aux deux côtés de l'équation.
- Facturez le trinôme carré parfait en l'écrivant sous la forme d'un binôme au carré à gauche et simplifiez en ajoutant les termes à droite.
- Utilisez la propriété Square Root.
- Simplifiez le radical, puis résolvez les deux équations résultantes.
- Vérifiez les solutions.


