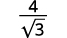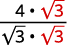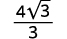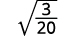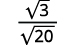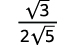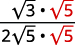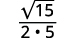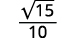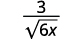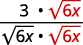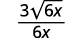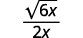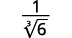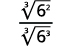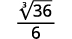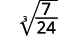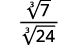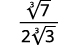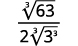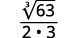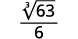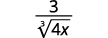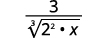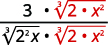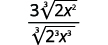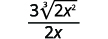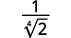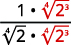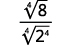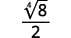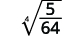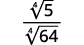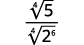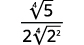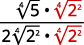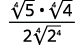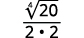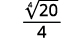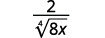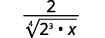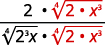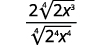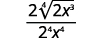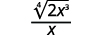8.6 : Diviser les expressions radicales
- Page ID
- 194288
À la fin de cette section, vous serez en mesure de :
- Divisez les expressions
- Rationaliser un dénominateur à un terme
- Rationaliser un dénominateur à deux termes
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifiez :\(\dfrac{30}{48}\).
Si vous avez oublié ce problème, consultez l'exemple 1.24. - Simplifiez :\(x^{2}⋅x^{4}\).
Si vous avez oublié ce problème, consultez l'exemple 5.12. - Multipliez :\((7+3x)(7−3x)\).
Si vous avez oublié ce problème, consultez l'exemple 5.32.
Divisez les expressions
Nous avons utilisé la propriété quotient des expressions radicales pour simplifier les racines des fractions. Nous devrons utiliser cette propriété « à l'envers » pour simplifier une fraction avec des radicaux. Nous donnons à nouveau la propriété quotient des expressions radicales pour faciliter la consultation. N'oubliez pas que nous supposons que toutes les variables sont supérieures ou égales à zéro, de sorte qu'aucune barre de valeur absolue n'est nécessaire.
Définition\(\PageIndex{1}\): Quotient Property of Radical Expressions
Si\(\sqrt[n]{a}\) et\(\sqrt[n]{b}\) sont des nombres réels\(b≠0\), et pour n'importe quel entier\(n≥2\) alors,
\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} \quad \text { and } \quad \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
Nous utiliserons la propriété quotient des expressions radicales lorsque la fraction avec laquelle nous commençons est le quotient de deux radicaux et qu'aucun des radicaux ne représente une puissance parfaite de l'indice. Lorsque nous écrivons la fraction dans un radical unique, nous pouvons trouver des facteurs communs dans le numérateur et le dénominateur.
Simplifiez :
- \(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
- \(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Solution :
un.
\(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
Réécrivez en utilisant la propriété du quotient,
\(\sqrt{\dfrac{72 x^{3}}{162 x}}\)
Supprimez les facteurs courants.
\(\sqrt{\dfrac{\cancel{18} \cdot 4 \cdot x^{2} \cdot \cancel{x}}{\cancel{18} \cdot 9 \cdot \cancel{x}}}\)
Simplifiez.
\(\sqrt{\dfrac{4 x^{2}}{9}}\)
Simplifiez le radical.
\(\dfrac{2 x}{3}\)
b.
\(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Réécrivez à l'aide de la propriété quotient,\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\).
\(\sqrt[3]{\dfrac{32 x^{2}}{4 x^{5}}}\)
Simplifiez la fraction sous le radical.
\(\sqrt[3]{\dfrac{8}{x^{3}}}\)
Simplifiez le radical.
\(\dfrac{2}{x}\)
Simplifiez :
- \(\dfrac{\sqrt{50 s^{3}}}{\sqrt{128 s}}\)
- \(\dfrac{\sqrt[3]{56 a}}{\sqrt[3]{7 a^{4}}}\)
- Réponse
-
- \(\dfrac{5s}{8}\)
- \(\dfrac{2}{a}\)
Simplifiez :
- \(\dfrac{\sqrt{75 q^{5}}}{\sqrt{108 q}}\)
- \(\dfrac{\sqrt[3]{72 b^{2}}}{\sqrt[3]{9 b^{5}}}\)
- Réponse
-
- \(\dfrac{5 q^{2}}{6}\)
- \(\dfrac{2}{b}\)
Simplifiez :
- \(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
- \(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Solution :
un.
\(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
Réécrivez à l'aide de la propriété quotient.
\(\sqrt{\dfrac{147 a b^{8}}{3 a^{3} b^{4}}}\)
Supprimez les facteurs communs de la fraction.
\(\sqrt{\dfrac{49 b^{4}}{a^{2}}}\)
Simplifiez le radical.
\(\dfrac{7 b^{2}}{a}\)
b.
\(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Réécrivez à l'aide de la propriété quotient.
\(\sqrt[3]{\dfrac{-250 m n^{-2}}{2 m^{-2} n^{4}}}\)
Simplifiez la fraction sous le radical.
\(\sqrt[3]{\dfrac{-125 m^{3}}{n^{6}}}\)
Simplifiez le radical.
\(-\dfrac{5 m}{n^{2}}\)
Simplifiez :
- \(\dfrac{\sqrt{162 x^{10} y^{2}}}{\sqrt{2 x^{6} y^{6}}}\)
- \(\dfrac{\sqrt[3]{-128 x^{2} y^{-1}}}{\sqrt[3]{2 x^{-1} y^{2}}}\)
- Réponse
-
- \(\dfrac{9 x^{2}}{y^{2}}\)
- \(\dfrac{-4 x}{y}\)
Simplifiez :
- \(\dfrac{\sqrt{300 m^{3} n^{7}}}{\sqrt{3 m^{5} n}}\)
- \(\dfrac{\sqrt[3]{-81 p q^{-1}}}{\sqrt[3]{3 p^{-2} q^{5}}}\)
- Réponse
-
- \(\dfrac{10 n^{3}}{m}\)
- \(\dfrac{-3 p}{q^{2}}\)
Simplifiez :\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Solution :
\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Réécrivez à l'aide de la propriété quotient.
\(\sqrt{\dfrac{54 x^{5} y^{3}}{3 x^{2} y}}\)
Supprimez les facteurs communs de la fraction.
\(\sqrt{18 x^{3} y^{2}}\)
Réécrivez le radicand en tant que produit en utilisant le plus grand facteur carré parfait.
\(\sqrt{9 x^{2} y^{2} \cdot 2 x}\)
Réécrivez le radical comme étant le produit de deux radicaux.
\(\sqrt{9 x^{2} y^{2}} \cdot \sqrt{2 x}\)
Simplifiez.
\(3 x y \sqrt{2 x}\)
Simplifiez :\(\dfrac{\sqrt{64 x^{4} y^{5}}}{\sqrt{2 x y^{3}}}\)
- Réponse
-
\(4 x y \sqrt{2 x}\)
Simplifiez :\(\dfrac{\sqrt{96 a^{5} b^{4}}}{\sqrt{2 a^{3} b}}\)
- Réponse
-
\(4 a b \sqrt{3 b}\)
Rationaliser un dénominateur à un terme
Avant que le calculateur ne devienne un outil de la vie quotidienne, l'approximation de la valeur d'une fraction avec un radical au dénominateur était un processus très fastidieux !
C'est pour cette raison qu'un processus appelé rationalisation du dénominateur a été développé. Une fraction dont le dénominateur est un radical est convertie en une fraction équivalente dont le dénominateur est un entier. Les racines carrées des nombres qui ne sont pas des carrés parfaits sont des nombres irrationnels. Lorsque nous rationalisons le dénominateur, nous écrivons une fraction équivalente avec un nombre rationnel dans le dénominateur. Ce processus est toujours utilisé aujourd'hui et est également utile dans d'autres domaines des mathématiques.
Définition\(\PageIndex{2}\): Rationalizing the Denominator
La rationalisation du dénominateur est le processus qui consiste à convertir une fraction ayant un radical dans le dénominateur en une fraction équivalente dont le dénominateur est un entier.
Même si des calculateurs sont disponibles presque partout, une fraction dont le dénominateur comporte un radical doit encore être rationalisée. Il n'est pas considéré comme simplifié si le dénominateur contient un radical.
De même, une expression radicale n'est pas considérée comme simplifiée si le radical et contient une fraction.
Expressions radicaux simplifiées
Une expression radicale est considérée comme simplifiée s'il y a
- aucun facteur du radical n'a la puissance parfaite de l'indice
- aucune fraction dans le radicand
- aucun radical dans le dénominateur d'une fraction
Pour rationaliser un dénominateur avec une racine carrée, nous utilisons la propriété qui\((\sqrt{a})^{2}=a\). Si on met au carré une racine carrée irrationnelle, on obtient un nombre rationnel.
Nous utiliserons cette propriété pour rationaliser le dénominateur dans l'exemple suivant.
Simplifiez :
- \(\dfrac{4}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{20}}\)
- \(\dfrac{3}{\sqrt{6 x}}\)
Solution :
Pour rationaliser un dénominateur à l'aide d'un terme, nous pouvons multiplier une racine carrée par elle-même. Pour maintenir l'équivalence de la fraction, nous multiplions le numérateur et le dénominateur par le même facteur.
un.
|
|
|
| Multipliez le numérateur et le dénominateur par\(\sqrt{3}\). |
|
| Simplifiez. |
|
b. On simplifie toujours d'abord le radical dans le dénominateur, avant de le rationaliser. De cette façon, les chiffres restent plus petits et plus faciles à utiliser.
|
|
|
| La fraction n'étant pas un carré parfait, réécrivez-la à l'aide de la propriété Quotient. |
|
| Simplifiez le dénominateur. |
|
| Multipliez le numérateur et le dénominateur par\(\sqrt{5}\). |
|
| Simplifiez. |
|
| Simplifiez. |
|
c.
|
|
|
| Multipliez le numérateur et le dénominateur par\(\sqrt{6x}\). |
|
| Simplifiez. |
|
| Simplifiez. |
|
Simplifiez :
- \(\dfrac{5}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{32}}\)
- \(\dfrac{2}{\sqrt{2 x}}\)
- Réponse
-
- \(\dfrac{5 \sqrt{3}}{3}\)
- \(\dfrac{\sqrt{6}}{8}\)
- \(\dfrac{\sqrt{2 x}}{x}\)
Simplifiez :
- \(\dfrac{6}{\sqrt{5}}\)
- \(\sqrt{\dfrac{7}{18}}\)
- \(\dfrac{5}{\sqrt{5 x}}\)
- Réponse
-
- \(\dfrac{6 \sqrt{5}}{5}\)
- \(\dfrac{\sqrt{14}}{6}\)
- \(\dfrac{\sqrt{5 x}}{x}\)
Lorsque nous avons rationalisé une racine carrée, nous avons multiplié le numérateur et le dénominateur par une racine carrée qui nous donnait un carré parfait sous le radical du dénominateur. Lorsque nous avons pris la racine carrée, le dénominateur n'avait plus de radical.
Nous suivrons un processus similaire pour rationaliser les racines supérieures. Pour rationaliser un dénominateur avec un radical d'indice supérieur, nous multiplions le numérateur et le dénominateur par un radical qui nous donnerait un radical qui est la puissance parfaite de l'indice. Lorsque nous simplifierons le nouveau radical, le dénominateur n'aura plus de radical.
Par exemple,
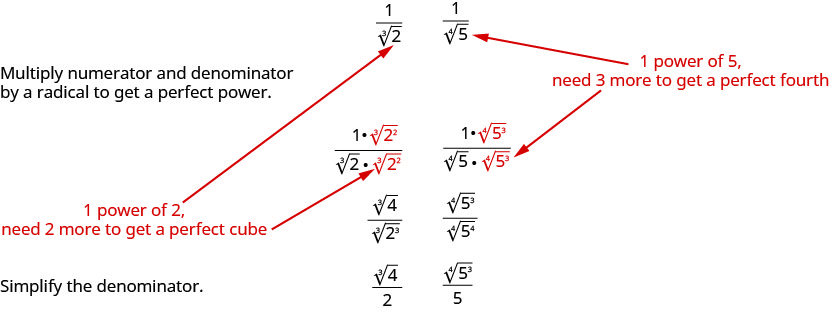
Nous utiliserons cette technique dans les prochains exemples.
Simplifiez :
- \(\dfrac{1}{\sqrt[3]{6}}\)
- \(\sqrt[3]{\dfrac{7}{24}}\)
- \(\dfrac{3}{\sqrt[3]{4 x}}\)
Solution :
Pour rationaliser un dénominateur avec une racine cubique, nous pouvons le multiplier par une racine cubique qui nous donnera un cube parfait dans le radical et dans le dénominateur. Pour maintenir l'équivalence de la fraction, nous multiplions le numérateur et le dénominateur par le même facteur.
un.
|
|
|
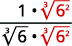
| Le radical du dénominateur a un facteur de\(6\). Multipliez à la fois le numérateur et le dénominateur par\(\sqrt[3]{6^{2}}\), ce qui nous donne\(2\) plus de facteurs de\(6\). |
|
| Multipliez. Remarquez que le radical dans le dénominateur a\(3\) les pouvoirs de\(6\). |
|
| Simplifiez la racine cubique dans le dénominateur. |
|
b. On simplifie toujours d'abord le radical dans le dénominateur, avant de le rationaliser. De cette façon, les chiffres restent plus petits et plus faciles à utiliser.
|
|
|
| La fraction n'étant pas un cube parfait, réécrivez-la à l'aide de la propriété Quotient. |
|
| Simplifiez le dénominateur. |
|
| Multipliez le numérateur et le dénominateur par\(\sqrt[3]{3^{2}}\). Cela nous donnera des\(3\) facteurs de\(3\). |
|
| Simplifiez. |
|
| N'oubliez pas,\(\sqrt[3]{3^{3}}=3\). |
|
| Simplifiez. |
|
c.
|
|
|
| Réécrivez le radicand pour montrer les facteurs. |
|
| Multipliez le numérateur et le dénominateur par\(\sqrt[3]{2 \cdot x^{2}}\). Cela nous permettra d'obtenir des\(3\) facteurs\(2\) et des\(3\) facteurs de\(x\). |
|
| Simplifiez. |
|
| Simplifiez le radical dans le dénominateur. |
|
Simplifiez :
- \(\dfrac{1}{\sqrt[3]{7}}\)
- \(\sqrt[3]{\dfrac{5}{12}}\)
- \(\dfrac{5}{\sqrt[3]{9 y}}\)
- Réponse
-
- \(\dfrac{\sqrt[3]{49}}{7}\)
- \(\dfrac{\sqrt[3]{90}}{6}\)
- \(\dfrac{5 \sqrt[3]{3 y^{2}}}{3 y}\)
Simplifiez :
- \(\dfrac{1}{\sqrt[3]{2}}\)
- \(\sqrt[3]{\dfrac{3}{20}}\)
- \(\dfrac{2}{\sqrt[3]{25 n}}\)
- Réponse
-
- \(\dfrac{\sqrt[3]{4}}{2}\)
- \(\dfrac{\sqrt[3]{150}}{10}\)
- \(\dfrac{2 \sqrt[3]{5 n^{2}}}{5 n}\)
Simplifiez :
- \(\dfrac{1}{\sqrt[4]{2}}\)
- \(\sqrt[4]{\dfrac{5}{64}}\)
- \(\dfrac{2}{\sqrt[4]{8 x}}\)
Solution :
Pour rationaliser un dénominateur avec une quatrième racine, nous pouvons multiplier par une quatrième racine qui nous donnera une quatrième puissance parfaite dans le radical et dans le dénominateur. Pour maintenir l'équivalence de la fraction, nous multiplions le numérateur et le dénominateur par le même facteur.
un.
|
|
|
| Le radical du dénominateur a un facteur de\(2\). Multipliez à la fois le numérateur et le dénominateur par\(\sqrt[4]{2^{3}}\), ce qui nous donne\(3\) plus de facteurs de\(2\). |
|
| Multipliez. Remarquez que le radical dans le dénominateur a\(4\) les pouvoirs de\(2\). |
|
| Simplifiez la quatrième racine du dénominateur. |
|
b. On simplifie toujours d'abord le radical dans le dénominateur, avant de le rationaliser. De cette façon, les chiffres restent plus petits et plus faciles à utiliser.
|
|
|
| La fraction n'étant pas une quatrième puissance parfaite, réécrivez-la en utilisant la propriété du quotient. |
|
| Réécrivez le radical et le dénominateur pour montrer les facteurs. |
|
| Simplifiez le dénominateur. |
|
| Multipliez le numérateur et le dénominateur par\(\sqrt[4]{2^{2}}\). Cela nous donnera des\(4\) facteurs de\(2\). |
|
| Simplifiez. |
|
| N'oubliez pas,\(\sqrt[4]{2^{4}}=2\). |
|
| Simplifiez. |
|
c.
|
|
|
| Réécrivez le radicand pour montrer les facteurs. |
|
| Multipliez le numérateur et le dénominateur par\(\sqrt[4]{2 \cdot x^{3}}\). Cela nous permettra d'obtenir des\(4\) facteurs\(2\) et des\(4\) facteurs de\(x\). |
|
| Simplifiez. |
|
| Simplifiez le radical dans le dénominateur. |
|
| Simplifiez la fraction. |
|
Simplifiez :
- \(\dfrac{1}{\sqrt[4]{3}}\)
- \(\sqrt[4]{\dfrac{3}{64}}\)
- \(\dfrac{3}{\sqrt[4]{125 x}}\)
- Réponse
-
- \(\dfrac{\sqrt[4]{27}}{3}\)
- \(\dfrac{\sqrt[4]{12}}{4}\)
- \(\dfrac{3 \sqrt[4]{5 x^{3}}}{5 x}\)
Simplifiez :
- \(\dfrac{1}{\sqrt[4]{5}}\)
- \(\sqrt[4]{\dfrac{7}{128}}\)
- \(\dfrac{4}{\sqrt[4]{4 x}}\)
- Réponse
-
- \(\dfrac{\sqrt[4]{125}}{5}\)
- \(\dfrac{\sqrt[4]{224}}{8}\)
- \(\dfrac{\sqrt[4]{64 x^{3}}}{x}\)
Rationaliser un dénominateur à deux termes
Lorsque le dénominateur d'une fraction est une somme ou une différence avec des racines carrées, nous utilisons le modèle du produit des conjugués pour rationaliser le dénominateur.
\(\begin{array}{c c}{(a-b)(a+b)} & {(2-\sqrt{5})(2+\sqrt{5})} \\ {a^{2}-b^{2}} &{ 2^{2}-(\sqrt{5})^{2}} \\ {}&{4-5} \\ {}&{-1}\end{array}\)
Lorsque nous multiplions un binôme qui inclut une racine carrée par son conjugué, le produit n'a pas de racines carrées.
Simplifiez :\(\dfrac{5}{2-\sqrt{3}}\)
Solution :
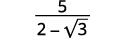 |
|
| Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. | 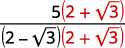 |
| Multipliez les conjugués dans le dénominateur. | 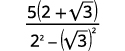 |
| Simplifiez le dénominateur. | 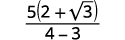 |
| Simplifiez le dénominateur. | 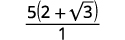 |
| Simplifiez. | 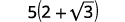 |
Simplifiez :\(\dfrac{3}{1-\sqrt{5}}\).
- Réponse
-
\(-\dfrac{3(1+\sqrt{5})}{4}\)
Simplifiez :\(\dfrac{2}{4-\sqrt{6}}\).
- Réponse
-
\(\dfrac{4+\sqrt{6}}{5}\)
Notez que nous n'avons pas distribué le\(5\) dans la réponse du dernier exemple. En laissant le résultat factorisé, nous pouvons voir s'il existe des facteurs qui peuvent être communs au numérateur et au dénominateur.
Simplifiez :\(\dfrac{\sqrt{3}}{\sqrt{u}-\sqrt{6}}\).
Solution :
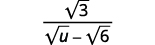 |
|
| Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. | 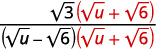 |
| Multipliez les conjugués dans le dénominateur. | 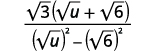 |
| Simplifiez le dénominateur. | 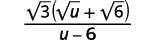 |
Simplifiez :\(\dfrac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- Réponse
-
\(\dfrac{\sqrt{5}(\sqrt{x}-\sqrt{2})}{x-2}\)
Simplifiez :\(\dfrac{\sqrt{10}}{\sqrt{y}-\sqrt{3}}\)
- Réponse
-
\(\dfrac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y-3}\)
Faites attention aux signes lors de la multiplication. Le numérateur et le dénominateur se ressemblent beaucoup lorsque vous multipliez par le conjugué.
Simplifiez :\(\dfrac{\sqrt{x}+\sqrt{7}}{\sqrt{x}-\sqrt{7}}\).
Solution :
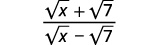 |
|
| Multipliez le numérateur et le dénominateur par le conjugué du dénominateur. |  |
| Multipliez les conjugués dans le dénominateur. | 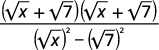 |
| Simplifiez le dénominateur. | 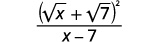 |
Nous ne mettons pas le numérateur au carré. Si nous le laissons sous forme factorielle, nous pouvons voir qu'il n'y a aucun facteur commun à supprimer du numérateur et du dénominateur.
Simplifiez :\(\dfrac{\sqrt{p}+\sqrt{2}}{\sqrt{p}-\sqrt{2}}\).
- Réponse
-
\(\dfrac{(\sqrt{p}+\sqrt{2})^{2}}{p-2}\)
Simplifiez :\(\dfrac{\sqrt{q}-\sqrt{10}}{\sqrt{q}+\sqrt{10}}\)
- Réponse
-
\(\dfrac{(\sqrt{q}-\sqrt{10})^{2}}{q-10}\)
Concepts clés
- Propriété de quotient des expressions radicales
- Si\(\sqrt[n]{a}\) et\(\sqrt[n]{b}\) sont des nombres réels\(b≠0\), et pour n'importe quel entier\(n≥2\) alors,\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\) et\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
- Expressions radicaux simplifiées
- Une expression radicale est considérée comme simplifiée s'il existe :
- aucun facteur dans le radical et qui possède les pouvoirs parfaits de l'indice
- aucune fraction dans le radicand
- aucun radical dans le dénominateur d'une fraction
- Une expression radicale est considérée comme simplifiée s'il existe :
Lexique
- rationaliser le dénominateur
- La rationalisation du dénominateur est le processus qui consiste à convertir une fraction ayant un radical dans le dénominateur en une fraction équivalente dont le dénominateur est un entier.