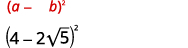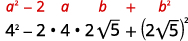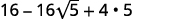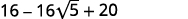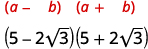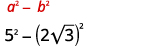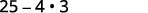Skip to main content
Global

8.5 : Ajouter, soustraire et multiplier des expressions radicales

  1. Last updated
  2. Save as PDF
  • Page ID
    194300

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Ajouter et soustraire des expressions radicales
    • Multipliez les expressions
    • Utiliser la multiplication polynomiale pour multiplier les expressions radicales

    Avant de commencer, répondez à ce questionnaire de préparation.

    1. Ajoutez :\(3x^{2}+9x−5−(x^{2}−2x+3)\).
      Si vous avez oublié ce problème, consultez l'exemple 5.5.
    2. Simplifiez :\((2+a)(4−a)\).
      Si vous avez oublié ce problème, consultez l'exemple 5.28.
    3. Simplifiez :\((9−5y)^{2}\).
      Si vous avez oublié ce problème, consultez l'exemple 5.31.

    Ajouter et soustraire des expressions radicales

    Ajouter des expressions radicales avec le même index et le même radicand revient à ajouter des termes similaires. Nous appelons radicaux ayant le même indice, le même radical et des radicaux similaires pour nous rappeler qu'ils fonctionnent de la même manière que des termes similaires.

    Définition\(\PageIndex{1}\): Like Radicals

    Les radicaux similaires sont des expressions radicales ayant le même indice et le même radicand.

    Nous ajoutons et soustrayons comme des radicaux de la même manière que nous ajoutons et soustrayons des termes similaires. Nous savons que\(3x+8x\) c'est le\(11x\) cas. De même, nous ajoutons\(3 \sqrt{x}+8 \sqrt{x}\) et le résultat est\(11 \sqrt{x}\).

    Pensez à ajouter des termes similaires avec des variables dans les exemples suivants. Lorsque vous avez des radicaux similaires, il suffit d'ajouter ou de soustraire les coefficients. Quand les radicaux ne sont pas semblables, on ne peut pas combiner les termes.

    Exemple\(\PageIndex{1}\)

    Simplifiez :

    1. \(2 \sqrt{2}-7 \sqrt{2}\)
    2. \(5 \sqrt[3]{y}+4 \sqrt[3]{y}\)
    3. \(7 \sqrt[4]{x}-2 \sqrt[4]{y}\)

    Solution :

    un.

    \(2 \sqrt{2}-7 \sqrt{2}\)

    Comme les radicaux sont similaires, on soustrait les coefficients.

    \(-5 \sqrt{2}\)

    b.

    \(5 \sqrt[3]{y}+4 \sqrt[3]{y}\)

    Comme les radicaux sont similaires, on ajoute les coefficients.

    \(9 \sqrt[3]{y}\)

    c.

    \(7 \sqrt[4]{x}-2 \sqrt[4]{y}\)

    Les indices sont les mêmes mais les radicaux sont différents. Ce ne sont pas des radicaux. Comme les radicaux ne sont pas similaires, on ne peut pas les soustraire.

    Exercice\(\PageIndex{1}\)

    Simplifiez :

    1. \(8 \sqrt{2}-9 \sqrt{2}\)
    2. \(4 \sqrt[3]{x}+7 \sqrt[3]{x}\)
    3. \(3 \sqrt[4]{x}-5 \sqrt[4]{y}\)
    Réponse
    1. \(-\sqrt{2}\)
    2. \(11 \sqrt[3]{x}\)
    3. \(3 \sqrt[4]{x}-5 \sqrt[4]{y}\)
    Exercice\(\PageIndex{2}\)

    Simplifiez :

    1. \(5 \sqrt{3}-9 \sqrt{3}\)
    2. \(5 \sqrt[3]{y}+3 \sqrt[3]{y}\)
    3. \(5 \sqrt[4]{m}-2 \sqrt[3]{m}\)
    Réponse
    1. \(-4 \sqrt{3}\)
    2. \(8 \sqrt[3]{y}\)
    3. \(5 \sqrt[4]{m}-2 \sqrt[3]{m}\)

    Pour que les radicaux soient similaires, ils doivent avoir le même indice et le même radical. Lorsque les radicandes contiennent plus d'une variable, tant que toutes les variables et leurs exposants sont identiques, les radicandes sont identiques.

    Exemple\(\PageIndex{2}\)

    Simplifiez :

    1. \(2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}\)
    2. \(\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}\)

    Solution :

    un.

    \(2 \sqrt{5 n}-6 \sqrt{5 n}+4 \sqrt{5 n}\)

    Comme les radicaux sont similaires, nous les combinons.

    \(0 \sqrt{5 n}\)

    Simplifiez.

    \(0\)

    b.

    \(\sqrt[4]{3 x y}+5 \sqrt[4]{3 x y}-4 \sqrt[4]{3 x y}\)

    Comme les radicaux sont similaires, nous les combinons.

    \(2 \sqrt[4]{3 x y}\)

    Exercice\(\PageIndex{3}\)

    Simplifiez :

    1. \(\sqrt{7 x}-7 \sqrt{7 x}+4 \sqrt{7 x}\)
    2. \(4 \sqrt[4]{5 x y}+2 \sqrt[4]{5 x y}-7 \sqrt[4]{5 x y}\)
    Réponse
    1. \(-2 \sqrt{7 x}\)
    2. \(-\sqrt[4]{5 x y}\)
    Exercice\(\PageIndex{4}\)

    Simplifiez :

    1. \(4 \sqrt{3 y}-7 \sqrt{3 y}+2 \sqrt{3 y}\)
    2. \(6 \sqrt[3]{7 m n}+\sqrt[3]{7 m n}-4 \sqrt[3]{7 m n}\)
    Réponse
    1. \(-\sqrt{3 y}\)
    2. \(3 \sqrt[3]{7 m n}\)

    N'oubliez pas que nous simplifions toujours les radicaux en retirant le facteur le plus important du radical et qui est une puissance de l'indice. Une fois que chaque radical est simplifié, nous pouvons décider s'ils sont similaires à des radicaux.

    Exemple\(\PageIndex{3}\)

    Simplifiez :

    1. \(\sqrt{20}+3 \sqrt{5}\)
    2. \(\sqrt[3]{24}-\sqrt[3]{375}\)
    3. \(\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}\)

    Solution :

    un.

    \(\sqrt{20}+3 \sqrt{5}\)

    Simplifiez les radicaux, lorsque cela est possible.

    \(\sqrt{4} \cdot \sqrt{5}+3 \sqrt{5}\)

    \(2 \sqrt{5}+3 \sqrt{5}\)

    Combinez les mêmes radicaux.

    \(5 \sqrt{5}\)

    b.

    \(\sqrt[3]{24}-\sqrt[3]{375}\)

    Simplifiez les radicaux.

    \(\sqrt[3]{8} \cdot \sqrt[3]{3}-\sqrt[3]{125} \cdot \sqrt[3]{3}\)

    \(2 \sqrt[3]{3}-5 \sqrt[3]{3}\)

    Combinez les mêmes radicaux.

    \(-3 \sqrt[3]{3}\)

    c.

    \(\frac{1}{2} \sqrt[4]{48}-\frac{2}{3} \sqrt[4]{243}\)

    Simplifiez les radicaux.

    \(\frac{1}{2} \sqrt[4]{16} \cdot \sqrt[4]{3}-\frac{2}{3} \sqrt[4]{81} \cdot \sqrt[4]{3}\)

    \(\frac{1}{2} \cdot 2 \cdot \sqrt[4]{3}-\frac{2}{3} \cdot 3 \cdot \sqrt[4]{3}\)

    \(\sqrt[4]{3}-2 \sqrt[4]{3}\)

    Combinez les mêmes radicaux.

    \(-\sqrt[4]{3}\)

    Exercice\(\PageIndex{5}\)

    Simplifiez :

    1. \(\sqrt{18}+6 \sqrt{2}\)
    2. \(6 \sqrt[3]{16}-2 \sqrt[3]{250}\)
    3. \(\frac{2}{3} \sqrt[3]{81}-\frac{1}{2} \sqrt[3]{24}\)
    Réponse
    1. \(9 \sqrt{2}\)
    2. \(2 \sqrt[3]{2}\)
    3. \(\sqrt[3]{3}\)
    Exercice\(\PageIndex{6}\)

    Simplifiez :

    1. \(\sqrt{27}+4 \sqrt{3}\)
    2. \(4 \sqrt[3]{5}-7 \sqrt[3]{40}\)
    3. \(\frac{1}{2} \sqrt[3]{128}-\frac{5}{3} \sqrt[3]{54}\)
    Réponse
    1. \(7 \sqrt{3}\)
    2. \(-10 \sqrt[3]{5}\)
    3. \(-3 \sqrt[3]{2}\)

    Dans l'exemple suivant, nous supprimerons les facteurs constants et variables des radicaux. Maintenant que nous nous sommes entraînés à prendre à la fois les racines paires et impaires des variables, il est courant à ce stade de supposer que toutes les variables sont supérieures ou égales à zéro afin que les valeurs absolues ne soient pas nécessaires. Nous utiliserons cette hypothèse tout au long de ce chapitre.

    Exemple\(\PageIndex{4}\)

    Simplifiez :

    1. \(9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}\)
    2. \(\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}\)

    Solution :

    un.

    \(9 \sqrt{50 m^{2}}-6 \sqrt{48 m^{2}}\)

    Simplifiez les radicaux.

    \(9 \sqrt{25 m^{2}} \cdot \sqrt{2}-6 \sqrt{16 m^{2}} \cdot \sqrt{3}\)

    \(9 \cdot 5 m \cdot \sqrt{2}-6 \cdot 4 m \cdot \sqrt{3}\)

    \(45 m \sqrt{2}-24 m \sqrt{3}\)

    Les radicaux ne sont pas similaires et ne peuvent donc pas être combinés.

    b.

    \(\sqrt[3]{54 n^{5}}-\sqrt[3]{16 n^{5}}\)

    Simplifiez les radicaux.

    \(\sqrt[3]{27 n^{3}} \cdot \sqrt[3]{2 n^{2}}-\sqrt[3]{8 n^{3}} \cdot \sqrt[3]{2 n^{2}}\)

    \(3 n \sqrt[3]{2 n^{2}}-2 n \sqrt[3]{2 n^{2}}\)

    Combinez les mêmes radicaux.

    \(n \sqrt[3]{2 n^{2}}\)

    Exercice\(\PageIndex{7}\)

    Simplifiez :

    1. \(\sqrt{32 m^{7}}-\sqrt{50 m^{7}}\)
    2. \(\sqrt[3]{135 x^{7}}-\sqrt[3]{40 x^{7}}\)
    Réponse
    1. \(-m^{3} \sqrt{2 m}\)
    2. \(x^{2} \sqrt[3]{5 x}\)
    Exercice\(\PageIndex{8}\)

    Simplifiez :

    1. \(\sqrt{27 p^{3}}-\sqrt{48 p^{3}}\)
    2. \(\sqrt[3]{256 y^{5}}-\sqrt[3]{32 n^{5}}\)
    Réponse
    1. \(-p \sqrt{3 p}\)
    2. \(4 y \sqrt[3]{4 y^{2}}-2 n \sqrt[3]{4 n^{2}}\)

    Multipliez les expressions

    Nous avons utilisé la propriété de produit des racines pour simplifier les racines carrées en supprimant les facteurs de carré parfaits. Nous pouvons utiliser la propriété de produit des racines « à l'envers » pour multiplier les racines carrées. N'oubliez pas que nous supposons que toutes les variables sont supérieures ou égales à zéro.

    Nous allons réécrire la propriété du produit de Roots afin de voir les deux côtés.

    Définition\(\PageIndex{2}\): Product Property of Roots

    Pour tous les nombres réels,\(\sqrt[n]{a}\) et\(\sqrt[b]{n}\), et pour tout entier\(n≥2\)

    \(\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b} \quad \text { and } \quad \sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}\)

    Lorsque nous multiplions deux radicaux, ils doivent avoir le même indice. Une fois que nous avons multiplié les radicaux, nous recherchons les facteurs qui constituent une puissance de l'indice et nous simplifions le radical chaque fois que cela est possible.

    Multiplier des radicaux par des coefficients est un peu comme multiplier des variables par des coefficients. Pour multiplier,\(4x⋅3y\) on multiplie les coefficients ensemble, puis les variables. Le résultat est\(12xy\). Gardez cela à l'esprit lorsque vous créez ces exemples.

    Exemple\(\PageIndex{5}\)

    Simplifiez :

    1. \((6 \sqrt{2})(3 \sqrt{10})\)
    2. \((-5 \sqrt[3]{4})(-4 \sqrt[3]{6})\)

    Solution :

    un.

    \((6 \sqrt{2})(3 \sqrt{10})\)

    Multipliez en utilisant la propriété du produit.

    \(18\sqrt{20}\)

    Simplifiez le radical.

    \(18 \sqrt{4} \cdot \sqrt{5}\)

    Simplifiez.

    \(18 \cdot 2 \cdot \sqrt{5}\)

    \(36 \sqrt{5}\)

    b.

    \((-5 \sqrt[3]{4})(-4 \sqrt[3]{6})\)

    Multipliez en utilisant la propriété du produit.

    \(20 \sqrt[3]{24}\)

    Simplifiez le radical.

    \(20 \sqrt[3]{8} \cdot \sqrt[3]{3}\)

    Simplifiez.

    \(20 \cdot 2 \cdot \sqrt[3]{3}\)

    \(40 \sqrt[3]{3}\)

    Exercice\(\PageIndex{9}\)

    Simplifiez :

    1. \((3 \sqrt{2})(2 \sqrt{30})\)
    2. \((2 \sqrt[3]{18})(-3 \sqrt[3]{6})\)
    Réponse
    1. \(12 \sqrt{15}\)
    2. \(-18 \sqrt[3]{2}\)
    Exercice\(\PageIndex{10}\)

    Simplifiez :

    1. \((3 \sqrt{3})(3 \sqrt{6})\)
    2. \((-4 \sqrt[3]{9})(3 \sqrt[3]{6})\)
    Réponse
    1. \(27 \sqrt{2}\)
    2. \(-36 \sqrt[3]{2}\)

    Nous suivons les mêmes procédures lorsqu'il y a des variables dans les radicands.

    Exemple\(\PageIndex{6}\)

    Simplifiez :

    1. \(\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})\)
    2. \(\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)\)

    Solution :

    un.

    \(\left(10 \sqrt{6 p^{3}}\right)(4 \sqrt{3 p})\)

    Multipliez.

    \(40 \sqrt{18 p^{4}}\)

    Simplifiez le radical.

    \(40 \sqrt{9 p^{4}} \cdot \sqrt{2}\)

    Simplifiez.

    \(40 \cdot 3 p^{2} \cdot \sqrt{3}\)

    \(120 p^{2} \sqrt{3}\)

    b. Lorsque les radicands impliquent de grands nombres, il est souvent avantageux de les factoriser afin de trouver les pouvoirs parfaits.

    \(\left(2 \sqrt[4]{20 y^{2}}\right)\left(3 \sqrt[4]{28 y^{3}}\right)\)

    Multipliez.

    \(6 \sqrt[4]{4 \cdot 5 \cdot 4 \cdot 7 y^{5}}\)

    Simplifiez le radical.

    \(6 \sqrt[4]{16 y^{4}} \cdot \sqrt[4]{35 y}\)

    Simplifiez.

    \(6 \cdot 2 y \sqrt[4]{35 y}\)

    Multipliez.

    \(12 y \sqrt[4]{35 y}\)

    Exercice\(\PageIndex{11}\)

    Simplifiez :

    1. \(\left(6 \sqrt{6 x^{2}}\right)\left(8 \sqrt{30 x^{4}}\right)\)
    2. \(\left(-4 \sqrt[4]{12 y^{3}}\right)\left(-\sqrt[4]{8 y^{3}}\right)\)
    Réponse
    1. \(36 x^{3} \sqrt{5}\)
    2. \(8 y \sqrt[4]{3 y^{2}}\)
    Exercice\(\PageIndex{12}\)

    Simplifiez :

    1. \(\left(2 \sqrt{6 y^{4}}\right)(12 \sqrt{30 y})\)
    2. \(\left(-4 \sqrt[4]{9 a^{3}}\right)\left(3 \sqrt[4]{27 a^{2}}\right)\)
    Réponse
    1. \(144 y^{2} \sqrt{5 y}\)
    2. \(-36 \sqrt[4]{3 a}\)

    Utiliser la multiplication polynomiale pour multiplier des expressions radicales

    Dans les prochains exemples, nous utiliserons la propriété distributive pour multiplier des expressions avec des radicaux. Nous allons d'abord distribuer puis simplifier les radicaux lorsque cela est possible.

    Exemple\(\PageIndex{7}\)

    Simplifiez :

    1. \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)
    2. \(\sqrt[3]{9}(5-\sqrt[3]{18})\)

    Solution :

    un.

    \(\sqrt{6}(\sqrt{2}+\sqrt{18})\)

    Multipliez.

    \(\sqrt{12}+\sqrt{108}\)

    Simplifiez.

    \(\sqrt{4} \cdot \sqrt{3}+\sqrt{36} \cdot \sqrt{3}\)

    Simplifiez.

    \(2 \sqrt{3}+6 \sqrt{3}\)

    Combinez comme des radicaux.

    \(8\sqrt{3}\)

    b.

    \(\sqrt[3]{9}(5-\sqrt[3]{18})\)

    Distribuez.

    \(5 \sqrt[3]{9}-\sqrt[3]{162}\)

    Simplifiez.

    \(5 \sqrt[3]{9}-\sqrt[3]{27} \cdot \sqrt[3]{6}\)

    Simplifiez.

    \(5 \sqrt[3]{9}-3 \sqrt[3]{6}\)

    Exercice\(\PageIndex{13}\)

    Simplifiez :

    1. \(\sqrt{6}(1+3 \sqrt{6})\)
    2. \(\sqrt[3]{4}(-2-\sqrt[3]{6})\)
    Réponse
    1. \(18+\sqrt{6}\)
    2. \(-2 \sqrt[3]{4}-2 \sqrt[3]{3}\)
    Exercice\(\PageIndex{14}\)

    Simplifiez :

    1. \(\sqrt{8}(2-5 \sqrt{8})\)
    2. \(\sqrt[3]{3}(-\sqrt[3]{9}-\sqrt[3]{6})\)
    Réponse
    1. \(-40+4 \sqrt{2}\)
    2. \(-3-\sqrt[3]{18}\)

    Lorsque nous travaillions avec des polynômes, nous multipliions les binômes par les binômes. N'oubliez pas que cela nous a donné quatre produits avant de combiner des termes similaires. Pour être sûrs d'obtenir les quatre produits, nous avons organisé notre travail, généralement selon la méthode FOIL.

    Exemple\(\PageIndex{8}\)

    Simplifiez :

    1. \((3-2 \sqrt{7})(4-2 \sqrt{7})\)
    2. \((\sqrt[3]{x}-2)(\sqrt[3]{x}+4)\)

    Solution :

    un.

    \((3-2 \sqrt{7})(4-2 \sqrt{7})\)

    Multipliez.

    \(12-6 \sqrt{7}-8 \sqrt{7}+4 \cdot 7\)

    Simplifiez.

    \(12-6 \sqrt{7}-8 \sqrt{7}+28\)

    Combinez les mêmes termes.

    \(40-14 \sqrt{7}\)

    b.

    \((\sqrt[3]{x}-2)(\sqrt[3]{x}+4)\)

    Multipliez.

    \(\sqrt[3]{x^{2}}+4 \sqrt[3]{x}-2 \sqrt[3]{x}-8\)

    Combinez les mêmes termes.

    \(\sqrt[3]{x^{2}}+2 \sqrt[3]{x}-8\)

    Exercice\(\PageIndex{15}\)

    Simplifiez :

    1. \((6-3 \sqrt{7})(3+4 \sqrt{7})\)
    2. \((\sqrt[3]{x}-2)(\sqrt[3]{x}-3)\)
    Réponse
    1. \(-66+15 \sqrt{7}\)
    2. \(\sqrt[3]{x^{2}}-5 \sqrt[3]{x}+6\)
    Exercice\(\PageIndex{16}\)

    Simplifiez :

    1. \((2-3 \sqrt{11})(4-\sqrt{11})\)
    2. \((\sqrt[3]{x}+1)(\sqrt[3]{x}+3)\)
    Réponse
    1. \(41-14 \sqrt{11}\)
    2. \(\sqrt[3]{x^{2}}+4 \sqrt[3]{x}+3\)
    Exemple\(\PageIndex{9}\)

    Simplifiez :\((3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})\)

    Solution :

    \((3 \sqrt{2}-\sqrt{5})(\sqrt{2}+4 \sqrt{5})\)

    Multipliez.

    \(3 \cdot 2+12 \sqrt{10}-\sqrt{10}-4 \cdot 5\)

    Simplifiez.

    \(6+12 \sqrt{10}-\sqrt{10}-20\)

    Combinez les mêmes termes.

    \(-14+11 \sqrt{10}\)

    Exercice\(\PageIndex{17}\)

    Simplifiez :\((5 \sqrt{3}-\sqrt{7})(\sqrt{3}+2 \sqrt{7})\)

    Réponse

    \(1+9 \sqrt{21}\)

    Exercice\(\PageIndex{18}\)

    Simplifiez :\((\sqrt{6}-3 \sqrt{8})(2 \sqrt{6}+\sqrt{8})\)

    Réponse

    \(-12-20 \sqrt{3}\)

    La reconnaissance de certains produits spéciaux nous a facilité le travail lorsque nous avons multiplié les binômes plus tôt. Cela est également vrai lorsque nous multiplions les radicaux. Les formules de produits spéciales que nous avons utilisées sont présentées ici.

    Produits spéciaux

    Carrés binomiaux

    \(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)

    Produit de conjugués

    \((a+b)(a-b)=a^{2}-b^{2}\)

    Nous utiliserons les formules spéciales des produits dans les prochains exemples. Nous allons commencer par le modèle de produit des carrés binomiaux.

    Exemple\(\PageIndex{10}\)

    Simplifiez :

    1. \(2+\sqrt{3})^{2}\)
    2. \((4-2 \sqrt{5})^{2}\)

    Solution :

    un.

      .
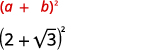    Multipliez en utilisant le modèle du produit des carrés binomiaux. .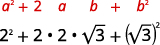
    Simplifiez. .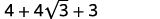
    Combinez les mêmes termes. .
    Tableau 8.4.1

    b.

    Tableau 8.4.2
     

    .
    Multiple, en utilisant le modèle du produit des carrés binomiaux.

    .
    Simplifiez.

    .
     

    .
    Combinez les mêmes termes.

    .
    Exercice\(\PageIndex{19}\)

    Simplifiez :

    1. \((10+\sqrt{2})^{2}\)
    2. \((1+3 \sqrt{6})^{2}\)
    Réponse
    1. \(102+20 \sqrt{2}\)
    2. \(55+6 \sqrt{6}\)
    Exercice\(\PageIndex{20}\)

    Simplifiez :

    1. \((6-\sqrt{5})^{2}\)
    2. \((9-2 \sqrt{10})^{2}\)
    Réponse
    1. \(41-12 \sqrt{5}\)
    2. \(121-36 \sqrt{10}\)

    Dans l'exemple suivant, nous utiliserons le modèle Product of Conjugués. Notez que le produit final ne contient aucun radical.

    Exemple\(\PageIndex{11}\)

    Simplifiez :\((5-2 \sqrt{3})(5+2 \sqrt{3})\)

    Solution :

     

    .
    Multipliez en utilisant le modèle du produit des conjugués.

    .
    Simplifiez.

    .
     

    .
    Tableau 8.4.3
    Exercice\(\PageIndex{21}\)

    Simplifiez :\((3-2 \sqrt{5})(3+2 \sqrt{5})\)

    Réponse

    \(-11\)

    Exercice\(\PageIndex{22}\)

    Simplifiez :\((4+5 \sqrt{7})(4-5 \sqrt{7})\)

    Réponse

    \(-159\)

    Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner à ajouter, soustraire et multiplier des expressions radicales.

    • Multiplier en ajoutant des radicaux soustrayants
    • Multiplier des produits spéciaux : binômes carrés contenant des racines carrées
    • Multiplier les conjugués

    Concepts clés

    • Propriété du produit Roots
      • Pour tous les nombres réels,\(\sqrt[n]{a}\) et\(\sqrt[n]{b}\), et pour tout entier\(n≥2\)\(\sqrt[n]{a b}=\sqrt[n]{a} \cdot \sqrt[n]{b}\) et\(\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a b}\)
    • Produits spéciaux

    \(\begin{array}{c c}{\text { Binomial Squares }}& {\text{Product of Conjugates}} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a+b)(a-b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)

    Lexique

    comme des radicaux
    Les radicaux similaires sont des expressions radicales ayant le même indice et le même radicand.