8.2 : Simplifier les expressions avec des racines
- Page ID
- 194282
À la fin de cette section, vous serez en mesure de :
- Simplifiez les expressions avec des
- Estimer et approximer les racines
- Simplifier les expressions variables avec des
Avant de commencer, répondez à ce questionnaire de préparation.
- Simplifier : a.\((−9)^{2}\) b.\(-9^{2}\) c.\((−9)^{3}\)
Si vous avez oublié ce problème, consultez l'exemple 2.21. - Arrondir\(3.846\) au centième le plus proche.
Si vous avez oublié ce problème, consultez l'exemple 1.34. - Simplifier : a.\(x^{3} \cdot x^{3}\) b.\(y^{2} \cdot y^{2} \cdot y^{2}\) c.\(z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}\)
Si vous avez oublié ce problème, consultez l'exemple 5.12.
Simplifiez les expressions grâce aux
Dans Foundations, nous avons brièvement examiné les racines carrées. N'oubliez pas que lorsqu'un nombre réel\(n\) est multiplié par lui-même, nous l'écrivons\(n^{2}\) et le lisons « au\(n^{2}\) carré ». Ce nombre est appelé le carré de\(n\), et\(n\) est appelé racine carrée. Par exemple,
\(13^{2}\)se lit comme suit : «\(13\) carré »
\(169\)est appelé le carré de\(13\), puisque\(13^{2}=169\)
\(13\)est une racine carrée de\(169\)
Carré
Si\(n^{2}=m\), alors\(m\) est le carré de\(n\).
Racine carrée
Si\(n^{2}=m\), alors\(n\) est une racine carrée de\(m\).
Remarquez\((−13)^{2} = 169\) également qu'il en\(−13\) va de même pour la racine carrée de\(169\). Par conséquent, les deux\(13\) et\(−13\) sont des racines carrées de\(169\).
Ainsi, chaque nombre positif a deux racines carrées : une positive et une négative. Et si nous ne voulions que la racine carrée positive d'un nombre positif ? Nous utilisons un signe radical, et écrivons\(\sqrt{m}\), qui indique la racine carrée positive de\(m\). La racine carrée positive est également appelée racine carrée principale.
Nous utilisons également le signe radical pour la racine carrée de zéro. Parce que\(0^{2}=0, \sqrt{0}=0\). Notez que zéro n'a qu'une seule racine carrée.
\(\sqrt{m}\)est lu « la racine carrée de »\(m\).
Si\(n^{2}=m\), alors\(n=\sqrt{m}\), pour\(n\geq 0\).
Nous savons que chaque nombre positif a deux racines carrées et que le signe radical indique la racine positive. Nous écrivons\(\sqrt{169}=13\). Si nous voulons trouver la racine carrée négative d'un nombre, nous plaçons un négatif devant le signe radical. Par exemple,\(-\sqrt{169}=-13\).
Simplifiez :
- \(\sqrt{144}\)
- \(-\sqrt{289}\)
Solution :
un.
\(\sqrt{144}\)
Depuis\(12^{2}=144\).
\(12\)
b.
\(-\sqrt{289}\)
Depuis\(17^{2}=289\) et le négatif se trouve devant le signe radical.
\(-17\)
Simplifiez :
- \(-\sqrt{64}\)
- \(\sqrt{225}\)
- Réponse
-
- \(-8\)
- \(15\)
Simplifiez :
- \(\sqrt{100}\)
- \(-\sqrt{121}\)
- Réponse
-
- \(10\)
- \(-11\)
Pouvons-nous simplifier\(-\sqrt{49}\) ? Y a-t-il un nombre dont le carré est\(-49\) ?
\((\)___\( )^{2}=-49\)
Tout nombre positif au carré est positif. Tout nombre négatif au carré est positif. Il n'y a pas de nombre réel égal à\(\sqrt{-49}\). La racine carrée d'un nombre négatif n'est pas un nombre réel.
Simplifiez :
- \(\sqrt{-196}\)
- \(-\sqrt{64}\)
Solution :
un.
\(\sqrt{-196}\)
Il n'y a pas de nombre réel dont le carré est\(-196\).
\(\sqrt{-196}\)n'est pas un vrai nombre.
b.
\(-\sqrt{64}\)
Le négatif se trouve devant le radical.
\(-8\)
Simplifiez :
- \(\sqrt{-169}\)
- \(-\sqrt{81}\)
- Réponse
-
- ce n'est pas un vrai chiffre
- \(-9\)
Simplifiez :
- \(-\sqrt{49}\)
- \(\sqrt{-121}\)
- Réponse
-
- \(-7\)
- ce n'est pas un vrai chiffre
Jusqu'à présent, nous n'avons parlé que de carrés et de racines carrées. Élargissons maintenant notre travail pour inclure des puissances supérieures et des racines plus élevées.
Passons d'abord en revue un peu de vocabulaire.
\(\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}\)
Les termes « carré » et « cube » proviennent des formules de l'aire d'un carré et du volume d'un cube.
Il sera utile de disposer d'un tableau des puissances des nombres entiers de\(−5\) à\(5\). Voir la Figure 8.1.2
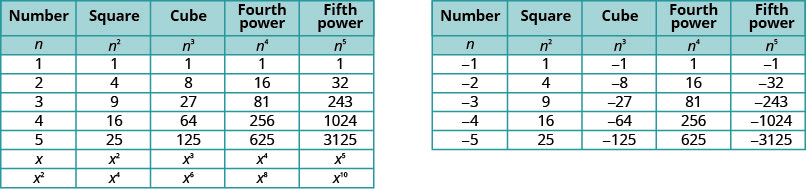
Remarquez les signes dans le tableau. Toutes les puissances des nombres positifs sont positives, bien entendu. Mais lorsque nous avons un nombre négatif, les puissances paires sont positives et les puissances impaires sont négatives. Nous allons copier la ligne avec les pouvoirs de\(−2\) pour vous aider à le voir.
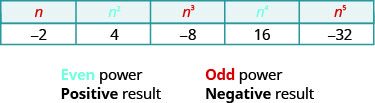
Nous allons maintenant étendre la définition de la racine carrée aux racines supérieures.
Si\(b^{n}=a\), alors\(b\) est une\(n^{th}\) racine de\(a\).
La\(n^{th}\) racine principale de\(a\) est écrite\(\sqrt[n]{a}\).
\(n\)C'est ce qu'on appelle l'indice du radical.
Tout comme nous utilisons le mot « cube » pour\(b^{3}\), nous utilisons le terme « racine cubique » pour\(\sqrt[3]{a}\).
Nous pouvons nous référer à la Figure 8.1.2 pour trouver des racines supérieures.
\(\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}\)
Pourrions-nous avoir une racine paire d'un nombre négatif ? Nous savons que la racine carrée d'un nombre négatif n'est pas un nombre réel. Il en va de même pour toute racine paire. Même les racines de nombres négatifs ne sont pas des nombres réels. Les racines impaires des nombres négatifs sont des nombres réels.
Propriétés de\(\sqrt[n]{a}\)
Quand\(n\) est un nombre pair et
- \(a \geq 0\),\(\sqrt[n]{a}\) est donc un nombre réel.
- \(a<0\), n'\(\sqrt[n]{a}\)est donc pas un nombre réel.
Quand\(n\) est un nombre impair,\(\sqrt[n]{a}\) est un nombre réel pour toutes les valeurs de\(a\).
Nous appliquerons ces propriétés dans les deux exemples suivants.
Simplifiez :
- \(\sqrt[3]{64}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{32}\)
Solution :
un.
\(\sqrt[3]{64}\)
Depuis\(4^{3}=64\).
\(4\)
b.
\(\sqrt[4]{81}\)
Depuis\((3)^{4}=81\).
\(3\)
c.
\(\sqrt[5]{32}\)
Depuis\((2)^{5}=32\).
\(2\)
Simplifiez :
- \(\sqrt[3]{27}\)
- \(\sqrt[4]{256}\)
- \(\sqrt[5]{243}\)
- Réponse
-
- \(3\)
- \(4\)
- \(3\)
Simplifiez :
- \(\sqrt[3]{1000}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{243}\)
- Réponse
-
- \(10\)
- \(2\)
- \(3\)
Dans cet exemple, soyez attentif aux signes négatifs ainsi qu'aux puissances paires et impaires.
Simplifiez :
- \(\sqrt[3]{-125}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{-243}\)
Solution :
un.
\(\sqrt[3]{-125}\)
Depuis\((-5)^{3}=-125\).
\(-5\)
b.
\(\sqrt[4]{16}\)
Pense,\((?)^{4}=-16\). Aucun nombre réel porté à la quatrième puissance n'est négatif.
Ce n'est pas un vrai chiffre.
c.
\(\sqrt[5]{-243}\)
Depuis\((-3)^{5}=-243\).
\(-3\)
Simplifiez :
- \(\sqrt[3]{-27}\)
- \(\sqrt[4]{-256}\)
- \(\sqrt[5]{-32}\)
- Réponse
-
- \(-3\)
- pas réel
- \(-2\)
Simplifiez :
- \(\sqrt[3]{-216}\)
- \(\sqrt[4]{-81}\)
- \(\sqrt[5]{-1024}\)
- Réponse
-
- \(-6\)
- pas réel
- \(-4\)
Estimation et racines approximatives
Lorsque nous voyons un nombre avec un signe radical, nous ne pensons souvent pas à sa valeur numérique. Bien que nous sachions probablement que le\(\sqrt{4}=2\), quelle est la valeur de\(\sqrt{21}\) ou\(\sqrt[3]{50}\) ? Dans certains cas, une estimation rapide est utile et dans d'autres, il est pratique d'avoir une approximation décimale.
Pour obtenir une estimation numérique d'une racine carrée, nous recherchons les nombres carrés parfaits les plus proches du radical. Pour trouver une estimation de\(\sqrt{11}\), nous voyons\(11\) entre des nombres carrés parfaits\(9\) et\(16\), plus près de\(9\). Sa racine carrée sera alors comprise entre\(3\) et\(4\), mais plus proche de\(3\).
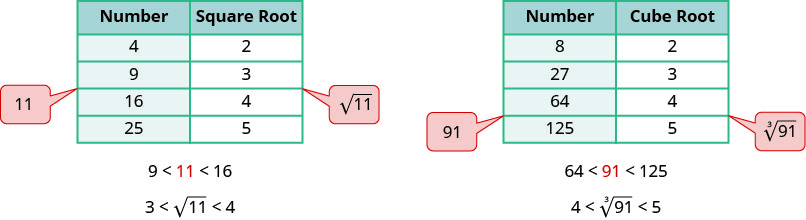
De même, pour estimer\(\sqrt[3]{91}\), nous voyons qu'\(91\)il se situe entre les nombres de cubes parfaits\(64\) et\(125\). La racine cubique sera alors comprise entre\(4\) et\(5\).
Estimez chaque racine entre deux nombres entiers consécutifs :
- \(\sqrt{105}\)
- \(\sqrt[3]{43}\)
Solution :
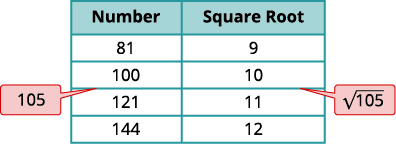
a. Pensez aux nombres carrés parfaits les plus proches de\(105\). Faites un petit tableau de ces carrés parfaits et de leurs racines carrées.
| \(\sqrt{105}\) | |
 |
|
| \(105\)Localisez-vous entre deux carrés parfaits consécutifs. | \(100<\color{red}105 \color{black} <121\) |
| \(\sqrt{105}\)se trouve entre leurs racines carrées. | \(10< \color{red}\sqrt{105}< \color{black}11\) |
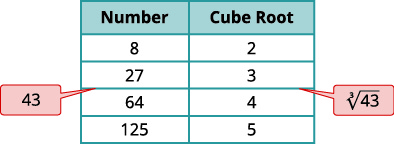
b. De même, nous nous situons\(43\) entre deux numéros de cube parfaits.
| \(\sqrt[3]{43}\) | |
 |
|
| \(43\)Localisez-vous entre deux cubes parfaits consécutifs. |  |
| \(\sqrt[3]{43}\)se trouve entre leurs racines cubiques. |  |
Estimez chaque racine entre deux nombres entiers consécutifs :
- \(\sqrt{38}\)
- \(\sqrt[3]{93}\)
- Réponse
-
- \(6<\sqrt{38}<7\)
- \(4<\sqrt[3]{93}<5\)
Estimez chaque racine entre deux nombres entiers consécutifs :
- \(\sqrt{84}\)
- \(\sqrt[3]{152}\)
- Réponse
-
- \(9<\sqrt{84}<10\)
- \(5<\sqrt[3]{152}<6\)
Il existe des méthodes mathématiques pour approximer les racines carrées, mais de nos jours, la plupart des gens utilisent un calculateur pour trouver les racines carrées. Pour trouver une racine carrée, vous allez utiliser la\(\sqrt{x}\) touche de votre calculatrice. Pour trouver une racine cubique, ou n'importe quelle racine avec un indice plus élevé, vous allez utiliser la\(\sqrt[y]{x}\) clé.
Lorsque vous utilisez ces touches, vous obtenez une valeur approximative. Il s'agit d'une approximation précise du nombre de chiffres affichés sur l'écran de votre calculatrice. Le symbole d'une approximation est\(≈\) et se lit comme suit : « approximativement ».
Supposons que votre calculatrice dispose d'\(10\)un affichage numérique. Tu verrais que
\(\sqrt{5} \approx 2.236067978\)arrondi à deux décimales est\(\sqrt{5} \approx 2.24\)
\(\sqrt[4]{93} \approx 3.105422799\)arrondi à deux décimales est\(\sqrt[4]{93} \approx 3.11\)
Comment savons-nous que ces valeurs sont des approximations et non des valeurs exactes ? Regardez ce qui se passe lorsque nous les mettons au point :
\(\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}\)
Leurs carrés sont proches de\(5\), mais ne sont pas exactement égaux à\(5\). Les quatrièmes pouvoirs sont proches\(93\), mais pas égaux à\(93\).
Arrondir à deux décimales :
- \(\sqrt{17}\)
- \(\sqrt[3]{49}\)
- \(\sqrt[4]{51}\)
Solution :
un.
\(\sqrt{17}\)
Utilisez la racine carrée de la calculatrice.
\(4.123105626 \dots\)
Arrondir à deux décimales.
\(4.12\)
\(\sqrt{17} \approx 4.12\)
b.
\(\sqrt[3]{49}\)
Utilisez la\(\sqrt[y]{x}\) touche de la calculatrice.
\(3.659305710 \ldots\)
Arrondir à deux décimales.
\(3.66\)
\(\sqrt[3]{49} \approx 3.66\)
c.
\(\sqrt[4]{51}\)
Utilisez la\(\sqrt[y]{x}\) touche de la calculatrice.
\(2.6723451177 \ldots\)
Arrondir à deux décimales.
\(2.67\)
\(\sqrt[4]{51} \approx 2.67\)
Arrondir à deux décimales :
- \(\sqrt{11}\)
- \(\sqrt[3]{71}\)
- \(\sqrt[4]{127}\)
- Réponse
-
- \(\approx 3.32\)
- \(\approx 4.14\)
- \(\approx 3.36\)
Arrondir à deux décimales :
- \(\sqrt{13}\)
- \(\sqrt[3]{84}\)
- \(\sqrt[4]{98}\)
- Réponse
-
- \(\approx 3.61\)
- \(\approx 4.38\)
- \(\approx 3.15\)
Simplifier les expressions variables avec des
La racine impaire d'un nombre peut être positive ou négative. Par exemple,
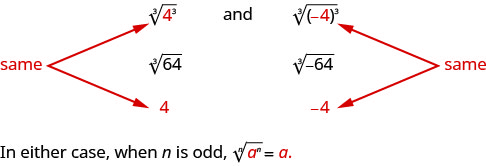
Mais qu'en est-il d'une racine uniforme ? Nous voulons la racine principale, donc\(\sqrt[4]{625}=5\).
Mais remarquez,
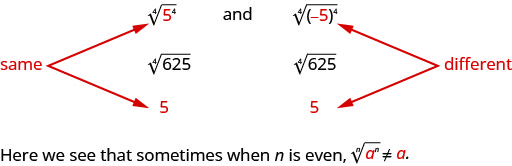
Comment pouvons-nous nous assurer que la quatrième racine de l'\(−5\)élévation à la quatrième puissance l'est\(5\) ? Nous pouvons utiliser la valeur absolue. \(|−5|=5\). Nous disons donc que quand\(n\) c'est égal\(\sqrt[n]{a^{n}}=|a|\). Cela garantit que la racine principale est positive.
Pour n'importe quel entier\(n\geq 2\),
lorsque l'indice\(n\) est impair\(\sqrt[n]{a^{n}}=a\)
lorsque l'indice\(n\) est pair\(\sqrt[n]{a^{n}}=|a|\)
Nous devons utiliser les signes de valeur absolue lorsque nous prenons la racine paire d'une expression avec une variable dans le radical.
Simplifiez :
- \(\sqrt{x^{2}}\)
- \(\sqrt[3]{n^{3}}\)
- \(\sqrt[4]{p^{4}}\)
- \(\sqrt[5]{y^{5}}\)
Solution :
a. Nous utilisons la valeur absolue pour être sûrs d'obtenir la racine positive.
\(\sqrt{x^{2}}\)
Puisque l'indice\(n\) est pair,\(\sqrt[n]{a^{n}}=|a|\).
b. Il s'agit d'une racine indexée étrange, donc aucun signe de valeur absolue n'est nécessaire.
\(\sqrt[3]{m^{3}}\)
Puisque l'indice\(n\) est impair,\(\sqrt[n]{a^{n}}=a\).
\(m\)
c.
\(\sqrt[4]{p^{4}}\)
Puisque l'indice\(n\) est pair\(\sqrt[n]{a^{n}}=|a|\).
\(|p|\)
d.
\(\sqrt[5]{y^{5}}\)
Puisque l'indice\(n\) est étrange,\(\sqrt[n]{a^{n}}=a\).
\(y\)
Simplifiez :
- \(\sqrt{b^{2}}\)
- \(\sqrt[3]{w^{3}}\)
- \(\sqrt[4]{m^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- Réponse
-
- \(|b|\)
- \(w\)
- \(|m|\)
- \(q\)
Simplifiez :
- \(\sqrt{y^{2}}\)
- \(\sqrt[3]{p^{3}}\)
- \(\sqrt[4]{z^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- Réponse
-
- \(|y|\)
- \(p\)
- \(|z|\)
- \(q\)
Qu'en est-il des racines carrées des puissances supérieures des variables ? La propriété de puissance des exposants dit\(\left(a^{m}\right)^{n}=a^{m \cdot n}\). Donc, si nous mettons au carré\(a^{m}\), l'exposant deviendra\(2m\).
\(\left(a^{m}\right)^{2}=a^{2 m}\)
Regardons maintenant la racine carrée.
\(\sqrt{a^{2 m}}\)
Depuis\(\left(a^{m}\right)^{2}=a^{2 m}\).
\(\sqrt{\left(a^{m}\right)^{2}}\)
Depuis,\(n\) c'est pair\(\sqrt[n]{a^{n}}=|a|\).
\(\left|a^{m}\right|\)
Donc\(\sqrt{a^{2 m}}=\left|a^{m}\right|\).
Nous appliquons ce concept dans l'exemple suivant.
Simplifiez :
- \(\sqrt{x^{6}}\)
- \(\sqrt{y^{16}}\)
Solution :
un.
\(\sqrt{x^{6}}\)
Depuis\(\left(x^{3}\right)^{2}=x^{6}\).
\(\sqrt{\left(x^{3}\right)^{2}}\)
Puisque l'indice\(n\) est pair\(\sqrt{a^{n}}=|a|\).
\(\left|x^{3}\right|\)
b.
\(\sqrt{y^{16}}\)
Depuis\(\left(y^{8}\right)^{2}=y^{16}\).
\(\sqrt{\left(y^{8}\right)^{2}}\)
Puisque l'indice\(n\) est pair\(\sqrt[n]{a^{n}}=|a|\).
\(y^{8}\)
Dans ce cas, le signe de valeur absolue n'est pas nécessaire, tout comme le\(y^{8}\) signe positif.
Simplifiez :
- \(\sqrt{y^{18}}\)
- \(\sqrt{z^{12}}\)
- Réponse
-
- \(|y^{9}|\)
- \(z^{6}\)
Simplifiez :
- \(\sqrt{m^{4}}\)
- \(\sqrt{b^{10}}\)
- Réponse
-
- \(m^{2}\)
- \(|b^{5}|\)
L'exemple suivant utilise la même idée pour les racines supérieures.
Simplifiez :
- \(\sqrt[3]{y^{18}}\)
- \(\sqrt[4]{z^{8}}\)
Solution :
un.
\(\sqrt[3]{y^{18}}\)
Depuis\(\left(y^{6}\right)^{3}=y^{18}\).
\(\sqrt[3]{\left(y^{6}\right)^{3}}\)
Puisque\(n\) c'est étrange,\(\sqrt[n]{a^{n}}=a\).
\(y^{6}\)
b.
\(\sqrt[4]{z^{8}}\)
Depuis\(\left(z^{2}\right)^{4}=z^{8}\).
\(\sqrt[4]{\left(z^{2}\right)^{4}}\)
Comme\(z^{2}\) c'est positif, nous n'avons pas besoin d'un signe de valeur absolue.
\(z^{2}\)
Simplifiez :
- \(\sqrt[4]{u^{12}}\)
- \(\sqrt[3]{v^{15}}\)
- Réponse
-
- \(|u^{3}|\)
- \(v^{5}\)
Simplifiez :
- \(\sqrt[5]{c^{20}}\)
- \(\sqrt[6]{d^{24}}\)
- Réponse
-
- \(c^{4}\)
- \(d^{4}\)
Dans l'exemple suivant, nous avons maintenant un coefficient devant la variable. Le concept\(\sqrt{a^{2 m}}=\left|a^{m}\right|\) fonctionne à peu près de la même manière.
\(\sqrt{16 r^{22}}=4\left|r^{11}\right|\)parce que\(\left(4 r^{11}\right)^{2}=16 r^{22}\).
Mais attention\(\sqrt{25 u^{8}}=5 u^{4}\) et aucun signe de valeur absolue ne sont nécessaires, comme c'\(u^{4}\)est toujours le cas pour le positif.
Simplifiez :
- \(\sqrt{16 n^{2}}\)
- \(-\sqrt{81 c^{2}}\)
Solution :
un.
\(\sqrt{16 n^{2}}\)
Depuis\((4 n)^{2}=16 n^{2}\).
\(\sqrt{(4 n)^{2}}\)
Puisque l'indice\(n\) est pair\(\sqrt[n]{a^{n}}=|a|\).
\(4|n|\)
b.
\(-\sqrt{81 c^{2}}\)
Depuis\((9 c)^{2}=81 c^{2}\).
\(-\sqrt{(9 c)^{2}}\)
Puisque l'indice\(n\) est pair\(\sqrt[n]{a^{n}}=|a|\).
\(-9|c|\)
Simplifiez :
- \(\sqrt{64 x^{2}}\)
- \(-\sqrt{100 p^{2}}\)
- Réponse
-
- \(8|x|\)
- \(-10|p|\)
Simplifiez :
- \(\sqrt{169 y^{2}}\)
- \(-\sqrt{121 y^{2}}\)
- Réponse
-
- \(13|y|\)
- \(-11|y|\)
Cet exemple pousse l'idée plus loin car elle a des racines d'indice plus élevé.
Simplifiez :
- \(\sqrt[3]{64 p^{6}}\)
- \(\sqrt[4]{16 q^{12}}\)
Solution :
un.
\(\sqrt[3]{64 p^{6}}\)
Réécrivez\(64p^{6}\) en tant que\(\left(4 p^{2}\right)^{3}\).
\(\sqrt[3]{\left(4 p^{2}\right)^{3}}\)
Prenez la racine cubique.
\(4p^{2}\)
b.
\(\sqrt[4]{16 q^{12}}\)
Réécrivez le radicand en tant que quatrième puissance.
\(\sqrt[4]{\left(2 q^{3}\right)^{4}}\)
Prenez la quatrième racine.
\(2|q^{3}|\)
Simplifiez :
- \(\sqrt[3]{27 x^{27}}\)
- \(\sqrt[4]{81 q^{28}}\)
- Réponse
-
- \(3x^{9}\)
- \(3|q^{7}|\)
Simplifiez :
- \(\sqrt[3]{125 q^{9}}\)
- \(\sqrt[5]{243 q^{25}}\)
- Réponse
-
- \(5p^{3}\)
- \(3q^{5}\)
Les exemples suivants comportent deux variables.
Simplifiez :
- \(\sqrt{36 x^{2} y^{2}}\)
- \(\sqrt{121 a^{6} b^{8}}\)
- \(\sqrt[3]{64 p^{63} q^{9}}\)
Solution :
un.
\(\sqrt{36 x^{2} y^{2}}\)
Depuis\((6 x y)^{2}=36 x^{2} y^{2}\)
\(\sqrt{(6 x y)^{2}}\)
Prenez la racine carrée.
\(6|xy|\)
b.
\(\sqrt{121 a^{6} b^{8}}\)
Depuis\(\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}\)
\(\sqrt{\left(11 a^{3} b^{4}\right)^{2}}\)
Prenez la racine carrée.
\(11\left|a^{3}\right| b^{4}\)
c.
\(\sqrt[3]{64 p^{63} q^{9}}\)
Depuis\(\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}\)
\(\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}\)
Prenez la racine cubique.
\(4p^{21}q^{3}\)
Simplifiez :
- \(\sqrt{100 a^{2} b^{2}}\)
- \(\sqrt{144 p^{12} q^{20}}\)
- \(\sqrt[3]{8 x^{30} y^{12}}\)
- Réponse
-
- \(10|ab|\)
- \(12p^{6}q^{10}\)
- \(2x^{10}y^{4}\)
Simplifiez :
- \(\sqrt{225 m^{2} n^{2}}\)
- \(\sqrt{169 x^{10} y^{14}}\)
- \(\sqrt[3]{27 w^{36} z^{15}}\)
- Réponse
-
- \(15|mn|\)
- \(13\left|x^{5} y^{7}\right|\)
- \(3w^{12}z^{5}\)
Accédez à cette ressource en ligne pour obtenir des instructions supplémentaires et vous entraîner à simplifier les expressions avec des racines.
- Simplification des exposants de variables avec des racines à l'aide
Concepts clés
- Notation à racine carrée
- \(\sqrt{m}\)est lu « la racine carrée de\(m\) »
- Si\(n^{2}=m\), alors\(n=\sqrt{m}\), pour\(n≥0\).
Graphique 8.1.1 - La racine carrée de\(m\),\(\sqrt{m}\), est un nombre positif dont le carré est\(m\).
- À la racine d'un nombre
- Si\(b^{n}=a\), alors\(b\) est une\(n^{th}\) racine de\(a\).
- La\(n^{th}\) racine principale de\(a\) est écrite\(\sqrt[n]{a}\).
- \(n\)est appelé indice du radical.
- Propriétés de\(\sqrt[n]{a}\)
- Quand\(n\) est un nombre pair et
- \(a≥0\), alors\(\sqrt[n]{a}\) est un nombre réel
- \(a<0\), alors n'\(\sqrt[n]{a}\)est pas un nombre réel
- Quand\(n\) est un nombre impair,\(\sqrt[n]{a}\) est un nombre réel pour toutes les valeurs de\(a\).
- Quand\(n\) est un nombre pair et
- Simplifier les racines paires et étranges
- Pour n'importe quel entier\(n≥2\),
- quand\(n\) c'est étrange\(\sqrt[n]{a^{n}}=a\)
- quand\(n\) est pair\(\sqrt[n]{a^{n}}=|a|\)
- Nous devons utiliser les signes de valeur absolue lorsque nous prenons la racine paire d'une expression avec une variable dans le radical.
- Pour n'importe quel entier\(n≥2\),
Lexique
- carré d'un nombre
- Si\(n^{2}=m\), alors\(m\) est le carré de\(n\).
- racine carrée d'un nombre
- Si\(n^{2}=m\), alors\(n\) est une racine carrée de\(m\).


